万物皆永续「翻译」

推荐理由：opyn 的研究团队提供了一个深刻又好理解的框架重新评估来链上衍生品。好的数学品味带来的优雅洞察：稳定币/借贷/AMM/Sqeeth 都是同一种衍生品。
翻译略有改动。推荐阅读原文：https://research.opyn.co/everything-is-a-perp

我们一直在深思熟虑关于幂永续合约这一产品。幂永续合约是指向指数价格的幂的资产，如 $index^2$ 或 $index^3$ 。这是一个引人入胜的思考黑洞。你越是思考幂永续合约，就越能看到一切都与幂永续合约有相似之处。

以下是我们得出的一些新颖的结论：

1. 数字货币质押类的稳定币（DAI or RAI）是 0-perps

2. 有保证金的期货（dydx）是 1-perps

3. 恒定积 AMM （uniswap）可以视为 0.5-perp 的投资组合，几何平均的 AMM （例如 Balancer） 是0-1 任何值的 perp 的投资组合。

这是很棒的结论，因为它揭示了 DeFi 的紧凑设计空间中三个基础元素。让我们逐一看一下，但首先我们需要定义 永续（perps） 和 幂（power perps）。

定义：永续合约是一种追踪指数并提供风险敞口的合约，标记价格（mark）距离目标价格（index）越远，定期支付的金额就越大。（有关更详细的解释，请参阅 The Cartoon Guide to Perps

从图形上看，资金支付随着资金周期内标记价格和追踪价格之间的区域变化而变化（见图）。如果标记价格高于指数，则多头支付空头费用。如果标记价格低于指数，则空头支付多头。

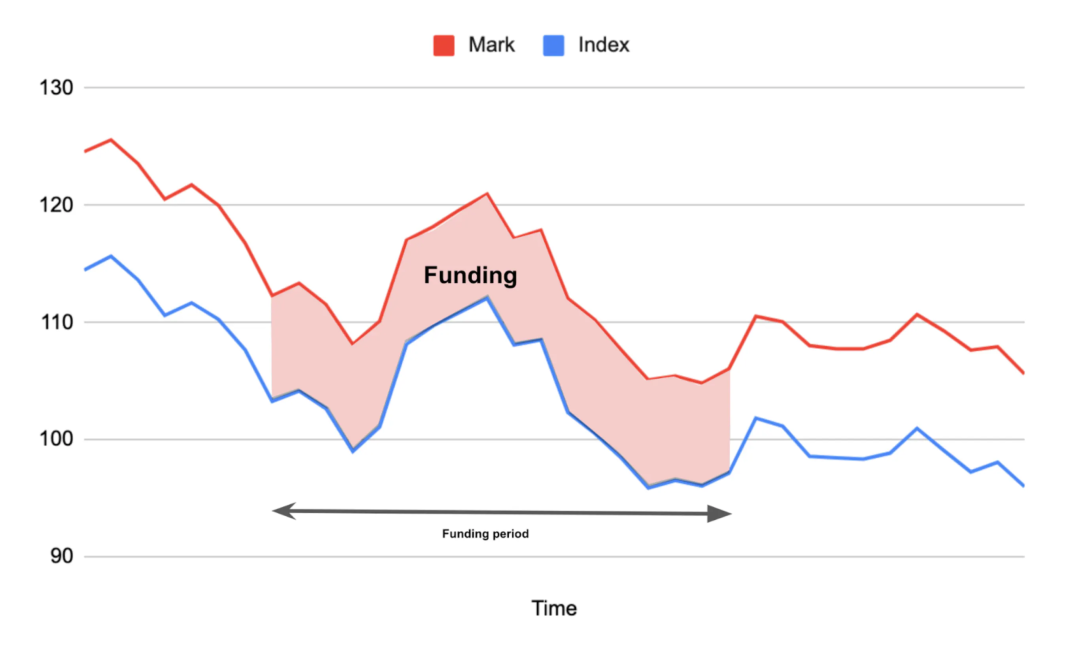
有各种转移资金支付的机制（例如，现金或实物支付、定期或连续支付、自动的费率或通过治理等），以及根据价格设定利率的各种机制（包括 Squeeth 使用的比例机制）以及 Reflexer 使用的更复杂的 PID 控制器）。所有机制都实现了这样的理念：当标记高于指数时，多头应该向空头支付，反之亦然。

定义：p - 幂永续产品是一个跟踪价格为 $(\text{index price})^p$ 的永续产品。要在幂永续合约中创建空头头寸，需要将一些抵押品锁定在金库中并铸造（即借入）一些幂永续合约。出售这种铸造的幂永续合约来做空。要想做多，就从拥有一些的人那里购买。该机制由所需的抵押品与债务比率驱动:

$$ Collateral\text{ } ratio= \frac{Debt}{Equity}\ = \frac{(perpetual\text{ } quantity)∗(index\text{ }asset\text{ }price) } {(collateral\text{ }quantity)∗(collateral\text{ }price)} $$

该比率必须安全地保持在 1 以上，以便有足够的抵押品来偿还债务，否则智能合约会通过购买足够的永续合约来平仓来清算抵押品。

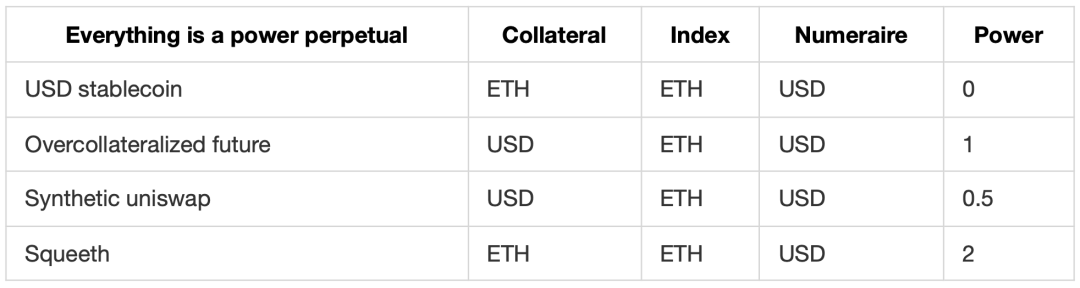
幂永续产品的设计空间

一个幂永续产品的设计需要确定「幂指数」，最小质押率 c>1，三种资产选择：

• 抵押品 例如 USD

• 追踪资产 例如 ETH

• 计价单位，通常是 USD

我们来看一下我们之前的结论

结论1:稳定币是 0-perps

稳定币是一种以可靠定价的抵押品为铸造代币的借贷。以下是美元稳定币设计：

• 抵押品 ETH

• 追踪资产 ETH

• 计价单位 USD

• 质押率 1.5

• 幂指数 0

这意味着我们可以投入 ETH 质押来构造出稳定币。跟踪指数是 ETH 价格的零次方，即 $ETH^0 = 1$

如果我质押 1 个 ETH，ETH 的价格在 $3000，我们可以最多构造 2000 个代币，质押率 1.5：

$$ Collateral \text{ } ratio= \frac{Debt}{Equity}\ = \frac{(perpetual\text{ } quantity)∗(index\text{ } asset\text{ } price)} {(collateral\text{ } quantity)∗(collateral \text{ }price)}=\frac{13000}{20001}=1.5 $$

资金费率是稳定币当前的美元交易价格（mark）减去 $ 目标价格^0$ 。

$$ Funding=Mark−Index =Mark−price^0 =Mark−1 $$

资金费率机制为稳定币的交易价格接近 1 美元提供了良好的激励。如果其交易价格大幅高于 1 美元，则出售您持有的任何稳定币，然后铸造并出售更多稳定币并获得资金将是有利可图的。如果低于 1 美元，则可以购买稳定币以获得正利率，并可能在未来以更高的价格出售。

并非所有的稳定币都使用这种精确的（标记 - 指数）融资机制，但所有有抵押的稳定币都共享这种基本结构，将稳定币作为良好抵押品的贷款。即使是具有治理设定利率的稳定币也会将其设置为类似于 mark - 1 的水平，以将其与 1 美元挂钩。

结论2:有保证金的期货是 1 perps

我们只需要讲结论 1 中的稳定币的幂指数改成 1 ，将抵押品改成 USD，我们得到了代币化的 ETH：

• 抵押品：USD

• 追踪资产：ETH

• 计价单位：USD

• 质押率：1.5

• 幂指数：1

例如当 ETH 交易价格为 3000 美元时，我用 4500 美元作为抵押，铸造了一个 ETH。

$$ \text{Collateral ratio} = \frac{\text{Equity}}{\text{Debt}} = \frac{(\text{collateral quantity}) \times (\text{collateral price})}{(\text{perpetual quantity}) \times (\text{index asset price})^p} = \frac{1 \times 4500}{3000^1 \times 1} = 1.5 $$

这个永续合约的资金费用是以美元计价的永续合约交易价格（标记价格）减去跟踪价格的一次幂。

$$ \text{Funding} = \text{Mark} - \text{Index} = \text{Mark} - \text{price}^1 = \text{Mark} - \text{ETH/USD price} $$

资金费率机制为永续合约的交易价格接近 ETH 价格提供了良好的激励。如果价格大幅高于 ETH 价格，资金费率会鼓励套利者购买资产并做空永续合约。如果价格大幅低于 ETH 价格，它将鼓励套利者卖空资产并购买永续合约。有一个精确的复制论点，基于提供 ETH 价格曝光的到期工具，应该基于什么来确定标记价格（参见关于永恒期权的论文。

我可以通过卖出我用 USD 构造的 ETH 来做空。

从代币化的空头资产转变为有保证金的空头永续合约

我们构造的稳定 ETH 资产的资本效率并不高。我们投入了 4500 美元的抵押品，以获得相当于 3000 美元（或 1 个 ETH）的 ETH 空头敞口。我们可以通过将代币出售给 USD 稳定币，然后使用这个作为抵押品来铸造更多的永续合约，从而提高资本效率。

如果最小抵押率是 1.5，ETH 的价格是 3000 美元，我们有以下步骤：

• 存入 4500 美元并铸造 1 个 ETH

• 将 ETH 卖出获得 3000 美元的收益，存入收益，并铸造  $\frac{1}{1.5} = 0.666$ 个 ETH

• 将 ETH 卖出获得 2000 美元的收益，存入收益，并铸造 $\left(\frac{1}{1.5}\right)^2 = 0.444$ 个 ETH

• 将 ETH 卖出获得 1333.33 美元的收益，存入收益，并铸造 $\left(\frac{1}{1.5}\right)^3 = 0.296$ 个 ETH

• 迭代下去

汇总这些交易，我们最终铸造并出售了 3 个 ETH。这是从 4500 美元的抵押品中获得的 9000 美元的 ETH 空头敞口。这个位置相当于开设了一个 2 倍杠杆的 ETH/USD 空头永续合约。如果我们可以使用闪电贷或者闪电兑换之类的工具，这个过程就会简化。我们可以以闪电兑换 3 个 ETH 为 USD，并使用收益作为抵押品来铸造 ETH 以偿还。如果抵押品要求是 110%，我们本可以建立一个 10 倍的头寸。

选择做多而不是做空

要做多，用美元购买这个稳定的 ETH。为了加杠杆做多，借用更多的美元使用稳定的 ETH 作为抵押，然后使用借来的美元购买更多的稳定 ETH，然后再借更多的美元并重复这个过程，直到 2 倍的 ETH。如果有闪电兑换或闪电贷可用，这可以在一次交易中完成。

所有这些意味着，超过 100% 的抵押品支持的永续合约可以转换为像在 dYdX 上交易的欠抵押的永续期货。

声明3：Uniswap 和其他恒定产品 CFMM 几乎是 0.5 指数的幂永续合约

在 Uniswap 池中的流动性位置的价值与两种资产的相对价格的平方根成正比。对于 ETH/USD 池中的全范围 LP，LP 的价值为

$$ V = 2(k(eth\text{ } price))^{0.5} $$

其中 k 是两种代币数量的乘积。池在每个周期内生成一定数量的交易费用。现在考虑这个幂永续合约：

• 抵押资产: USD

• 目标资产: ETH

• 计价单位: USD

• 质押率: 1.2

• 幂指数: 0.5

这份永续追踪 $price^{0.5}$ ，这也反映在 AMM 的收益上。

我们可以使用 0.5perp 复制：做空 $2*k^{0.5}$ 单位的永续，LP 则会收到资金费率和 AMM 手续费的差值。这样组合我们排除了价格风险，0.5 永续的价值应该在 $price^{0.5}$ ，准确的说：

$$ Uni\text{ } Fee = Index - Mark $$

扩展到 uniswap v3 也并不难，可以参考：https://papers.ssrn.com/sol3/papers.cfm?abstract_id=3898384，留给读者自己证明。

这给我们一个很好的结果，即 Uniswap 的市场均衡费用（实际上，这意味着如果年化波动率是 90%，你需要能收到 $1/8*0.9^2 = 10.125\%$ 的手续费回报率。如果你投入 100U 到全价格范围，你需要每天至少挣得 $0.028 来弥补无常损失。这等价于一个 0.5 perp 的资金费率为每天 2.8bp。）应该是 0.5 永续合约的资金费率。在零利率的简化情况下，可以推导出：

$$ Equilibrium\text{ }uniswap\text{ }return= \frac{\sigma^2}{8} $$

其中，$\sigma^2$ 是一个池资产相对于另一个资产的价格回报的方差。我们也可以从 Uniswap 的角度得出这个结果（参见：https://arxiv.org/pdf/1911.03380.pdf ，有更直接的构造例子）。我们也在（https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4317072 ) 里详细讨论了幂永续合约的角度

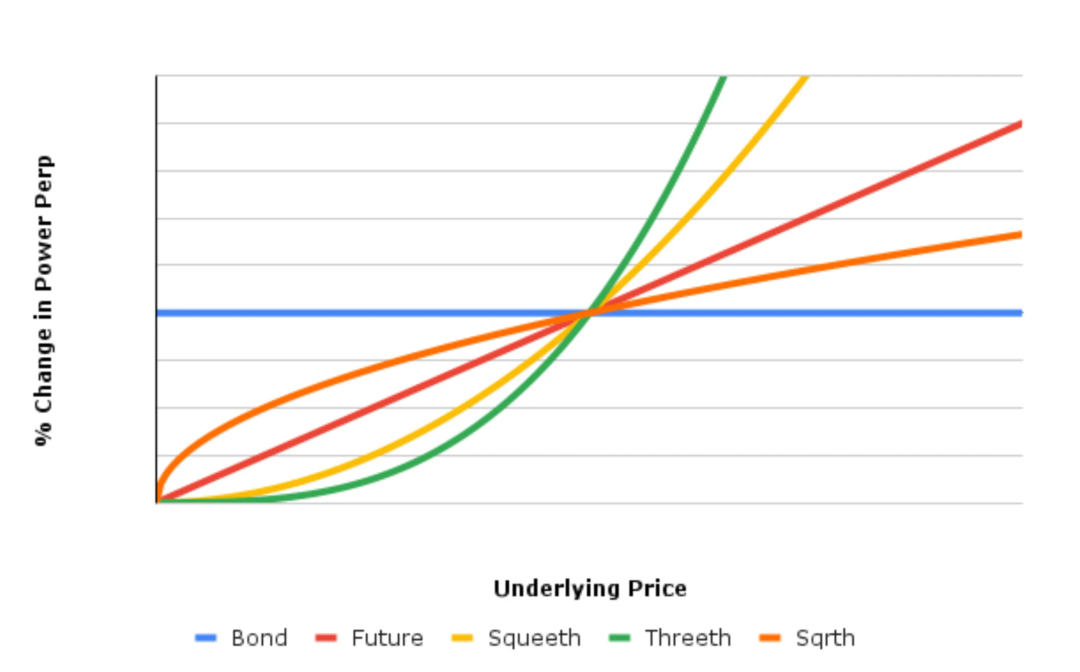
无穷的幂永续

我们发现稳定币/AMM/充分质押的永续期货都属于幂永续。

还漏了什么

更高阶的幂永续合约 - 从二次幂永续合约开始。Squeeth，第一个二次幂永续合约，提供了对价格风险二次成分的纯粹暴露。我们可以通过结合更高阶的幂永续合约和 1-perps（期货）以及 0-perps 作为抵押品，得到许多收益的良好近似。

如果我们想做的更精准，我们可以通过全部种类的永续期权，根据泰勒展开的权重来近似任意的 payoff： $sin(x),e^{x^2},log(x)$ ，你能想到的都可以构造。

下一步我们干什么

一个允许幂永续合约、抵押资产和 Uniswap LPs 良好互动的世界可能会非常有趣。