零知识证明 - 说说Binius
- Star Li
- 发布于 2024-05-28 09:49
- 阅读 3772
Binius是个新颖的零知识证明系统,目的是降低证明者的计算开销。Binius能降低证明开销的原因是使用了$F_2$以及扩展域。
好久都没写文章了。去年大段时间都在翻译PAZK。歇了一段时间,最近发现零知识证明技术有些新的方向和变化。感叹,总是有些有趣的人做着有趣的事情。羡慕,并努力让自己有趣。先说说Binius。Binius是个新颖的零知识证明系统,目的是降低证明者的计算开销。Binius能降低证明开销的原因是使用了$F_2$以及扩展域。
$F_2$以及扩展域
如果一个域K属于域L,则域L称为域K的扩展,域K称为域L的子域。如果域K是域F的扩展,用 K/F表示。如果p(x)是一个在域K上不可约减的多项式,则$L = K[X]/(p(X))$为域K的扩展,并且L中包含多项式p(X)的根。不可约减多项式指的是在某个域上没有根。
举个例子,$F_2$是一个域,其中只有两个值:0和1。通过$F_2[X]/(X^2+X+1)$可以获得域$F_4$,其中包括四个值:0,1,$\alpha$以及 $1+ \alpha$。该域上的加法(+)和乘法(.)计算表如下:
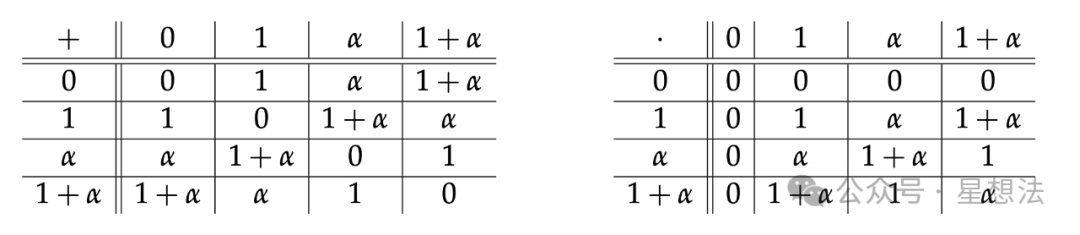
表格来自:https://www.math.uci.edu/~ndonalds/math120b/4extension.pdf(第五页)
以$\alpha (\alpha + 1)$的计算为例,$\alpha (\alpha + 1) = \alpha + \alpha^2 = \alpha - (\alpha + 1) = 1 $(因为 $1+\alpha + 1 = \alpha$)。
理论证明,通过上述指定不可约减多项式的方式,$F_2$域存在扩展域$F_2*n$。这种域的扩展,一层套一层,也称为“塔”。
线性编码(Linear Code)
对一个有限域F来说,如果一个编码中的“码字” (codeword)是$F^n$的子集,则这个编码是线性的。也就是说,线性编码中的码字的线性组合还是在这个编码中。编码中的“不相交”码字的个数称为编码的维度。举个例子,编码{00, 01,10,11}的维度是2,因为不相交的码字是{01,10}。码字之间的海明距离(Hamming distance)指的是码字间不同元素个数的最小值。
通常用{n, k, d}来表示一个线性编码,表示一个编码维度是k,码字长度为n,码字间的距离为d。强调一下的是,Reed–Solomon编码也是线性编码。其编码由n点组成,维度为k(k < n) (多项式的阶)。
Binius的多项式承诺方案
Binius的论文提供了多项式承诺方案的两个版本,一个是简单版本(3.7),一个是通用版本(3.11)。通用版本,基于$F_2$以及扩展设计。简单版本,基于一个小域和域扩展设计。讲讲简单版本,容易理解设计思路。简单版本的设计如下:

整个设计包括如下几个阶段:
-
设置( Setup ):原始数据基于域K,其长度为$2^l$。数据将分为两个部分(类似矩阵),两部分的长度分别是$m_0$和$m_1$。一个编码[n, m_1, d],将$m_1$维度的数据扩展到长度n。
-
承诺( Commit ):输入数据$t = (t_0, ..., t^{2^l-1})$,分成两部分,形成大小为$m_0 x m_1$的矩阵$(t_i){i=0}^{m_0 -1}$。每一行的数据,进行设置中的编码,生成$u_i$。对$u_i$,进行Merkle承诺,其承诺值为c。也就是说,所有编码后的“矩阵”数据承诺为c。
-
打开( Open ):用部分分支信息尝试打开承诺,并确认和扩展后的数据的距离小于$d/2$。
-
证明和验证( Prove & Verify ):通过Fiat-Shamir,生成随机挑战信息,证明者需要证明: $t(r_0, ..., r{l-1}) = s$。注意,其中的$r_0, ..., r{l-1}$ 属于域L。
-
证明者需要提供: 1/ $\gamma$ 个Merkle分支的证明信息 2/ 一个矩阵和向量的乘积结果t'
-
验证者首先验证随机挑选出的Merkle分支,是否是正确的编码(Enc)结果(编码后的线性组合的结果应该和线性组合后的编码结果相同)。并通过上表中的最后一个公式计算出正确的s结果,并和证明者提供的s值进行比较。
直观上,该多项式承诺方案,将一个大的多项式,切割成多个小的多项式,并通过编码进行扩展。通过随机检查部分编码结果的方式,确保这些小多项式是低次多项式(Proximity)。通过这些多项式的拉格朗日集,巧妙地计算出最后的多项式结果。
熟悉MLE(多线性多项式)的小伙伴,一眼可以看出t'的计算采用了MLE形式。

对于$2^v$个值来说,$X_w$展开为:
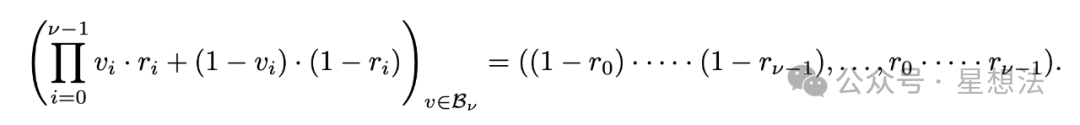
在Binius的多项式承诺方案中,因为t(x)的$2^l$个取值按照矩阵排列(m_0*m_1),则多线性扩展后的t(r)取值也分成两部分,横/竖各算一次。
Vitalik博客的一张图,更直观形象地描述了多项式承诺的流程:
https://vitalik.eth.limo/images/binius/binius.drawio.png
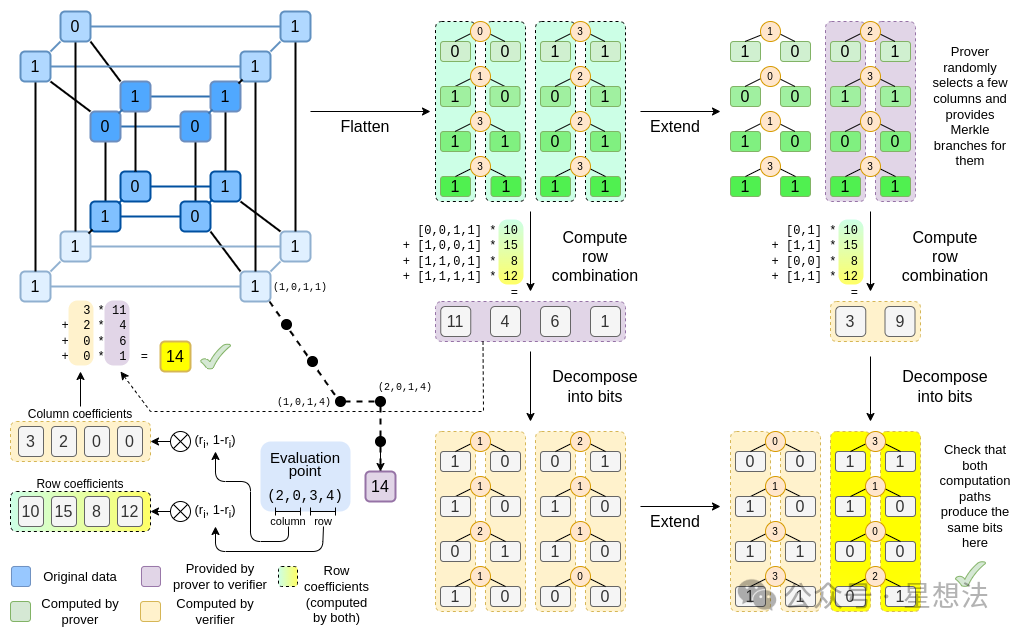
其中,(11,4,6,1)为t',s=14。
基于该多项式承诺方案,Binius在PLONK算术化的基础上设计了完整的零知识证明算法。感兴趣的小伙伴可以自行查看论文第5章。
Binius性能数据
在域大小“差不多”的情况下,$F_2$的塔式扩展域的计算资源是其他域的1/5。
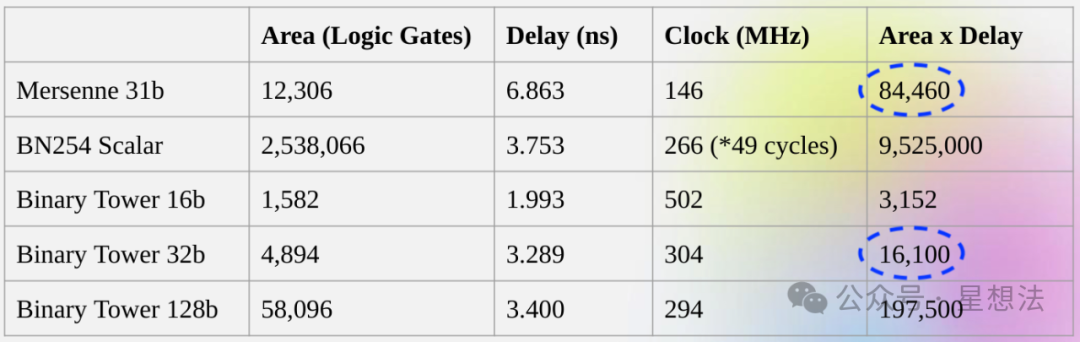
得益此,Binius多项式承诺方案的证明性能差不多是FRI(基于Goldilocks-64,Poseidon算法)性能的22倍。具体的测试方法和测试环境请查看论文第六章。Binius改善了证明生成时间,但是,验证时间也显著变长并且变量个数在$2^32$,证明的大小在M级。
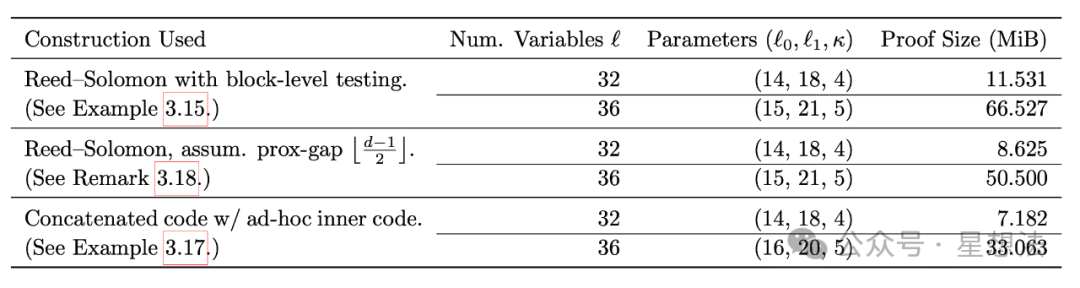
当然,验证时间和证明大小的问题,可以通过“连接”其他SNARK/STARK证明系统改善。
总结:
Binius是一种新型的零知识证明系统。Binius基于$F_2$以及扩展域,结合编码实现多项式承诺方案,证明性能显著提高,但是,验证时间显著变长,证明大小在M级。
参考资料:
0/https://eprint.iacr.org/2023/1784
1/https://blog.lambdaclass.com/climbing-the-tower-field-extensions/
2/https://vitalik.eth.limo/general/2024/04/29/binius.html
3/https://blog.lambdaclass.com/snarks-on-binary-fields-binius/
4/https://blog.lambdaclass.com/binius-part-2/

- zERC20 在 Arbitrum 上线:最完备 L2 的原生隐私 59 浏览
- 零知识编年史:群 33 浏览
- 以太坊执行层优化:状态树与虚拟机 165 浏览
- 首批 ZK 漏洞利用事件已发生,但它们并非我们所预期 167 浏览
- 首次 ZK 攻击发生,且出乎意料 193 浏览
- Vitalik: 以太坊量子抵抗路线图 143 浏览
- zkMesh:2026年2月回顾 184 浏览
- 失效的 Groth16 `delta == gamma == G2 生成元` 148 浏览
- 量子可恢复的 Zcash 164 浏览
- ZK编年史:哈希登场 242 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 441 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 364 浏览

