Web3
深入解析 Uniswap V2 的手续费计算:公式推导与代码详解
- 寻月隐君
- 发布于 2024-07-31 15:22
- 阅读 4501
深入解析UniswapV2的手续费计算:公式推导与代码详解UniswapV2的手续费计算
Uniswap V2 的手续费计算
1. 通过增发 share 的方式把手续费给项目方
$$ x \cdot y = k $$
$$ L = \sqrt{x \cdot y} = \sqrt{k} $$
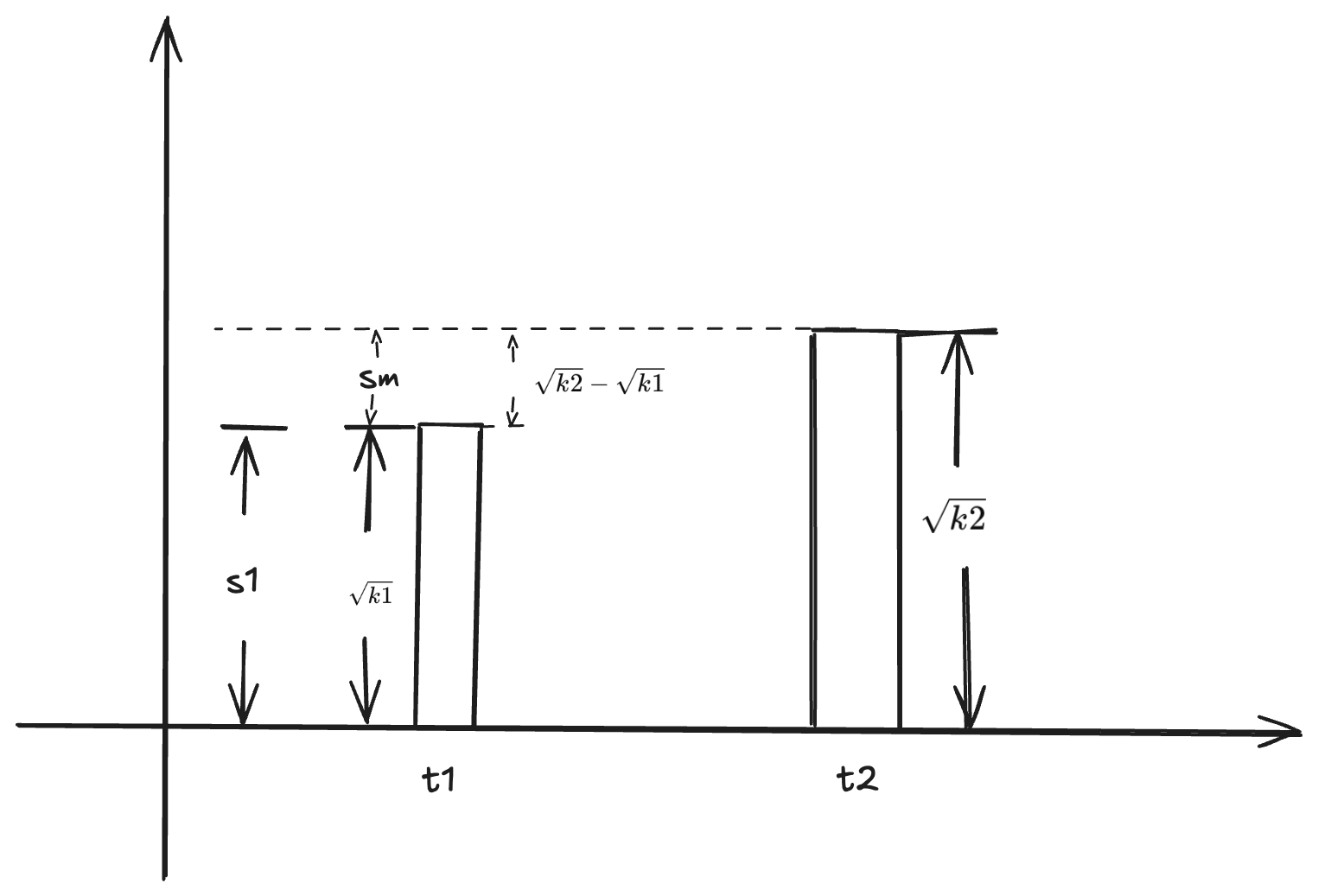 $$
\frac{Sm}{Sm + S1} = \frac{\sqrt{k2} - \sqrt{k1}}{\sqrt{k2}}
$$
$$
\frac{Sm}{Sm + S1} = \frac{\sqrt{k2} - \sqrt{k1}}{\sqrt{k2}}
$$
求 Sm
我们需要从方程
$$ \frac{Sm}{Sm + S1} = \frac{\sqrt{k2} - \sqrt{k1}}{\sqrt{k2}} $$ 中解出 Sm。
解题步骤
-
整理方程:
从方程中我们可以得到: $$ \frac{Sm}{Sm + S1} = \frac{\sqrt{k2} - \sqrt{k1}}{\sqrt{k2}} $$
-
交叉相乘:
将分数的两边交叉相乘,得到: $$ Sm \cdot \sqrt{k2} = (\sqrt{k2} - \sqrt{k1}) \cdot (Sm + S1) $$
-
展开右侧:
展开右侧的括号: $$ Sm \cdot \sqrt{k2} = (\sqrt{k2} - \sqrt{k1}) \cdot Sm + (\sqrt{k2} - \sqrt{k1}) \cdot S1 $$
-
将 ( Sm ) 相关项移到一边:
将含 ( Sm ) 的项移到方程的一侧: $$ Sm \cdot \sqrt{k2} - (\sqrt{k2} - \sqrt{k1}) \cdot Sm = (\sqrt{k2} - \sqrt{k1}) \cdot S1 $$
-
提取 ( Sm ):
提取 ( Sm ): $$ Sm \cdot (\sqrt{k2} - (\sqrt{k2} - \sqrt{k1})) = (\sqrt{k2} - \sqrt{k1}) \cdot S1 $$ 简化括号中的表达式: $$ \sqrt{k2} - (\sqrt{k2} - \sqrt{k1}) = \sqrt{k1} $$ 所以: $$ Sm \cdot \sqrt{k1} = (\sqrt{k2} - \sqrt{k1}) \cdot S1 $$
-
解出 Sm :
通过除以$\sqrt{k1}$解出Sm:
$$ Sm = \frac{(\sqrt{k2} - \sqrt{k1}) \cdot S1}{\sqrt{k1}} $$
最终结果
$$ Sm = \frac{(\sqrt{k2} - \sqrt{k1}) \cdot S1}{\sqrt{k1}} $$
2. 通过使 S1 增值的方式把手续费给 LP
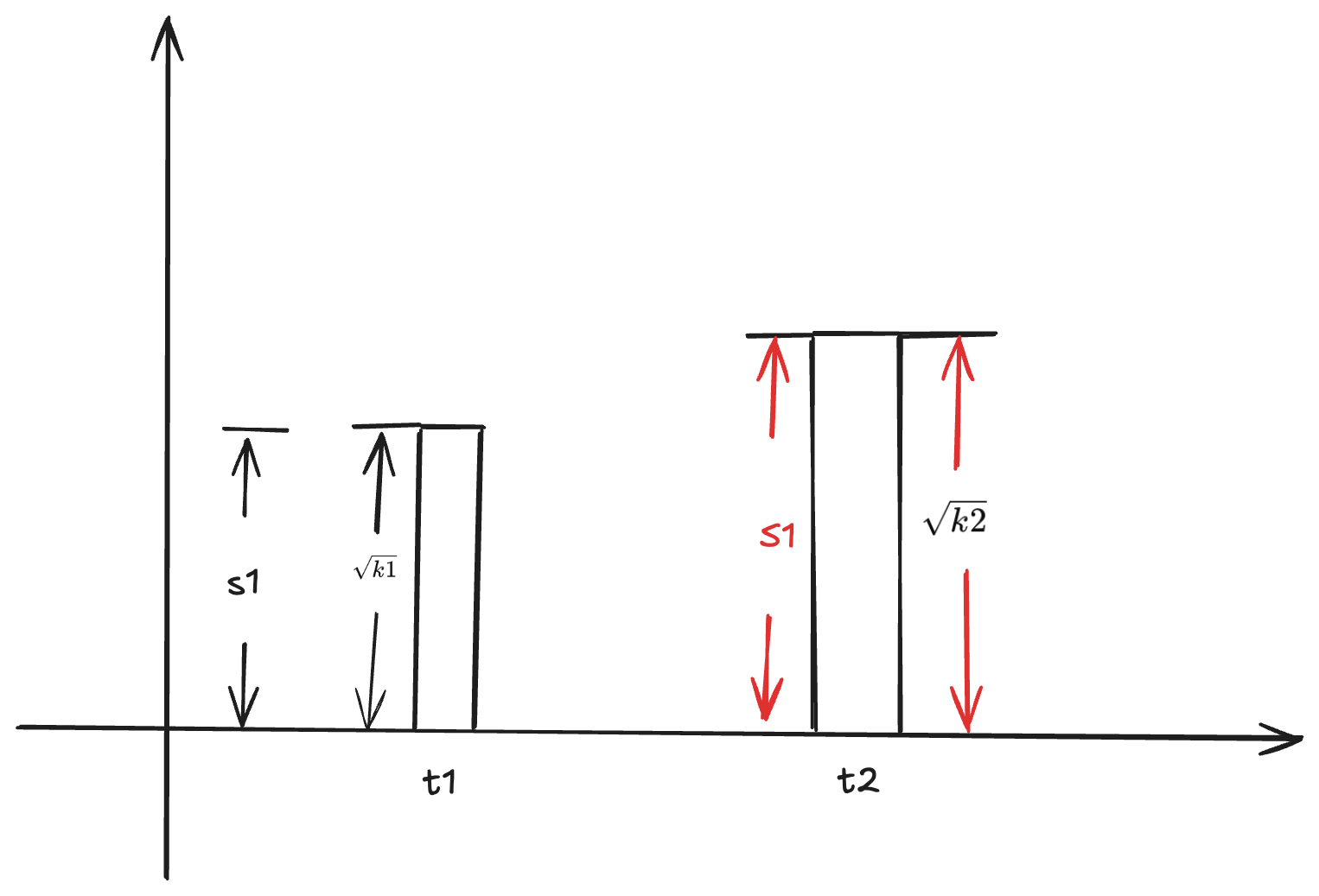
原来 S1 => $\sqrt{k1}$
现在 S1 = $\sqrt{k2}$
增值比例 $$ \frac{\sqrt{k2} - \sqrt{k1}}{\sqrt{k1}} $$ LP Token
1 LPT => $(1 + \frac{\sqrt{k2} - \sqrt{k1}}{\sqrt{k1}})$ $\sqrt{k2}$ > $\sqrt{k1}$
1 LPT => 1 token A => $(1 + \frac{\sqrt{k2} - \sqrt{k1}}{\sqrt{k1}})$ token A
1 LPT => 1 token B => $(1 + \frac{\sqrt{k2} - \sqrt{k1}}{\sqrt{k1}})$ token B
3. 项目方想分走手续费里的一定比例,该比例用 $\Phi$ 表示
Uniswap V2 的手续费计算
增值又增发
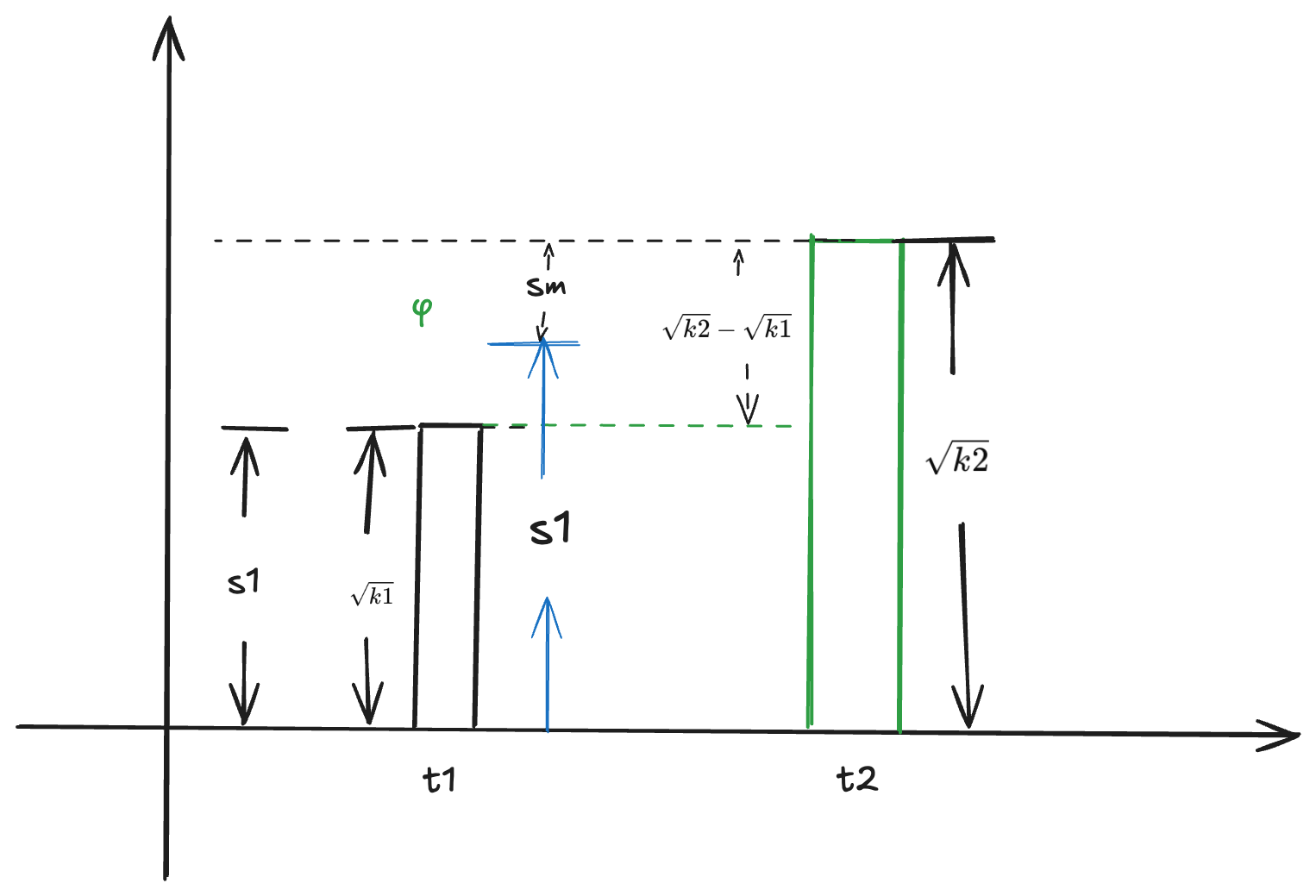
$$ \frac{Sm}{Sm + S1} = \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1})}{\sqrt{k2}} $$
求 Sm
我们通过以下步骤来推导:
原始公式
原始公式是:
$$ \frac{Sm}{Sm + S1} = \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1})}{\sqrt{k2}} $$
交叉相乘
首先,将公式两边交叉相乘以消除分母:
$$ Sm \cdot \sqrt{k2} = \phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot (Sm + S1) $$
展开和重新排列
展开右侧的表达式:
$$ Sm \cdot \sqrt{k2} = \phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot Sm + \phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot S1 $$ 将包含 ( Sm ) 的项移到一边:
$$ Sm \cdot \sqrt{k2} - \phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot Sm = \phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot S1 $$ 提取 ( Sm ):
$$ Sm \cdot \left(\sqrt{k2} - \phi \cdot (\sqrt{k2} - \sqrt{k1})\right) = \phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot S1 $$
简化
分母部分可以简化为:
$$ \sqrt{k2} - \phi \cdot \sqrt{k2} + \phi \cdot \sqrt{k1} $$ 进一步简化为:
$$ \left(1 - \phi\right) \cdot \sqrt{k2} + \phi \cdot \sqrt{k1} $$
求解 ( Sm )
将分母形式替换回公式中,得到:
$$ Sm = \frac{\phi \cdot (\sqrt{k2} - \sqrt{k1}) \cdot S1}{\left(1 - \phi\right) \cdot \sqrt{k2} + \phi \cdot \sqrt{k1}} $$
将分母部分进行化简
我们需要将分母部分调整成适当的形式。可以通过对分母进行重新表达来实现这一点:
$$ (1 - \phi) \cdot \sqrt{k2} + \phi \cdot \sqrt{k1} $$ 首先,我们从分母部分开始:
$$ (1 - \phi) \cdot \sqrt{k2} + \phi \cdot \sqrt{k1} $$ 为了将其变形为$ \frac{1}{\phi} - 1$ 的形式,我们可以使用以下变换:
- 计算 $\frac{1}{\phi} - 1$:
这两个表达式相等的原因可以通过简单的代数变换来解释。我们将证明以下等式:
$$ \frac{1}{\phi} - 1 = \frac{1 - \phi}{\phi} $$
证明过程
-
开始于左侧表达式:
$$ \frac{1}{\phi} - 1 $$
-
将 1 变成分母为 $\phi$的分数:
我们知道 1 可以写成 $\frac{\phi}{\phi}$。因此,我们有:
$$ \frac{1}{\phi} - 1 = \frac{1}{\phi} - \frac{\phi}{\phi} $$
-
合并分数:
为了合并这两个分数,我们需要它们具有相同的分母。现在它们都有分母 (\phi),可以合并为一个分数:
$$ \frac{1 - \phi}{\phi} $$
总结
通过代数变换,我们可以看到:
$$ \frac{1}{\phi} - 1 = \frac{1 - \phi}{\phi} $$ 这说明这两个表达式是相等的。...
