【Uniswap V2】| 详解 TWAP 价格预言机和使用举例

什么是价格

在 Uniswap 中，价格被定义为一种比率，即流动性池中一种资产的储备量与另一种资产的储备量之比。通常，我们更关注的资产会放在分母的位置。

例如，如果一个流动性池中包含 2 个 ETH 和 5000 个 USDT，我们想要计算 ETH 的价格，就将 ETH 的储备量放在分母，即：

$\frac{5000 \, \text{USDT}}{2 \, \text{ETH}} = 2500 \, \frac{\text{USDT}}{\text{ETH}}$

那么相对来说，USDT 的价格为：

$\frac{2 \, \text{ETH}}{5000 \, \text{USDT}} = 0.0004 \, \frac{\text{ETH}}{\text{USDT}}$

Uniswap 使用有着 112 位精度的定点数库来表示价格，“小数部分”存储在最右边的 112 位，“整数部分”存储在最左边的 112 位，总共占用 224 位。通常我们都是使用 18 位精度来表示十进制的定点数，大约对应的是二进制的 60 位精度，那么为什么我们要使用 UQ112x112 类型来存放价格呢？

因为两个资产的价格是“对称的”，当有个资产占用整数位数很多时，那么另一个资产占用的小数相当来说就很多，所以采用整数和小数存放精度一致的定点数类型。

想更多了解定点数的运算，可以看我之前发的文章 Solidity 中定点数的运算 。

设计 TWAP（时间加权平均价格）的原因

如果一个合约仅依赖于 Uniswap 合约中的瞬时价格来执行业务，就容易受到闪电贷攻击。这种攻击允许攻击者通过闪电贷在单笔交易中引发价格剧烈波动，从而执行对其有利的逻辑。

Uniswap V2 的预言机通过以下两种方式来防御这种攻击：

1. 价格获取采用先前时间段价格的平均值。
2. 计算平均价格时，不包括当前块中的价格。

然而，这并不意味着基于 TWAP 的预言机对价格操纵攻击完全安全。如果资产流动性不足，或计算平均值的时间窗口较短，攻击者仍然可以长期操控价格。

TWAP 实现原理

TWAP 根据价格在某一水平上维持的时间来加权计算。

通常，TWAP 的公式为：

$\text{time-weighted average price} = \frac{P_1 T_1 + P_2 T_2 + \cdots + P_n Tn}{\sum{i=1}^{n} T_i}$

其中，$T$ 表示一个持续的时间段，而不是时间戳，代表价格维持在某个水平的时长。

由于不同用户关注的平均价格时间段不同，Uniswap V2 合约仅存储公式中的分子部分。当流动性比例发生变化时（例如在 mint、burn、swap 或 sync 操作后），合约会更新 price0CumulativeLast 和 price1CumulativeLast 这两个变量。

contract UniswapV2Pair {
  ...
  uint32 private blockTimestampLast;
  uint public price0CumulativeLast;
  uint public price1CumulativeLast;
  ...
  // update reserves and, on the first call per block, price accumulators
  function _update(uint balance0, uint balance1, uint112 _reserve0, uint112 _reserve1) private {
    ...
    uint32 blockTimestamp = uint32(block.timestamp % 2**32);
    uint32 timeElapsed = blockTimestamp - blockTimestampLast;
    if (timeElapsed > 0 && _reserve0 != 0 && _reserve1 != 0) {
      // * never overflows, and + overflow is desired
      price0CumulativeLast += uint(UQ112x112.encode(_reserve1).uqdiv(_reserve0)) * timeElapsed;
      price1CumulativeLast += uint(UQ112x112.encode(_reserve0).uqdiv(_reserve1)) * timeElapsed;
    }
    blockTimestampLast = blockTimestamp;
    ...
  }
}

通过图像可以更直观地理解 TWAP 的原理。假设时间为横轴，价格为纵轴，那么每一秒钟的价格变化可以绘制成下图所示的矩形。此处我们假设出块时间一秒一块。

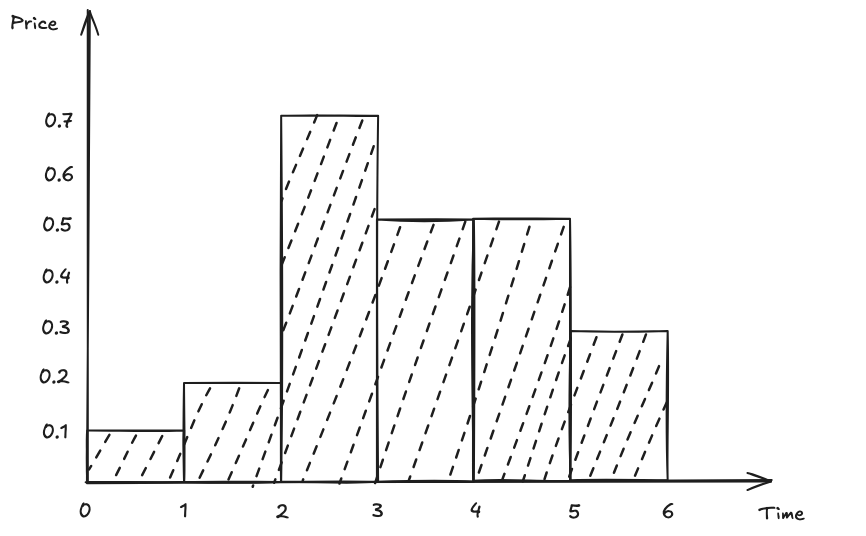
每个矩形的面积之和就是 TWAP 公式中的分子部分，即 price0CumulativeLast 或 price1CumulativeLast 的值。随着时间的推移，矩形面积不断累积，因此 price0CumulativeLast 和 price1CumulativeLast 也在持续增加。

当我们需要计算某一时间段的平均价格时，只需将该时间段内的矩形面积之和除以该时间段的长度。

从代码中可以注意到，每个区块内，累积价格仅更新一次，且只在区块内的第一笔触发 _update() 函数的交易时更新。此时的 _reserve0 和 _reserve1 是上一个区块的最后一笔触发 _update() 的储备量数据。因此，累积价格不包含当前区块的最新价格，而是基于上一个区块的价格，从而进一步防止价格操纵。

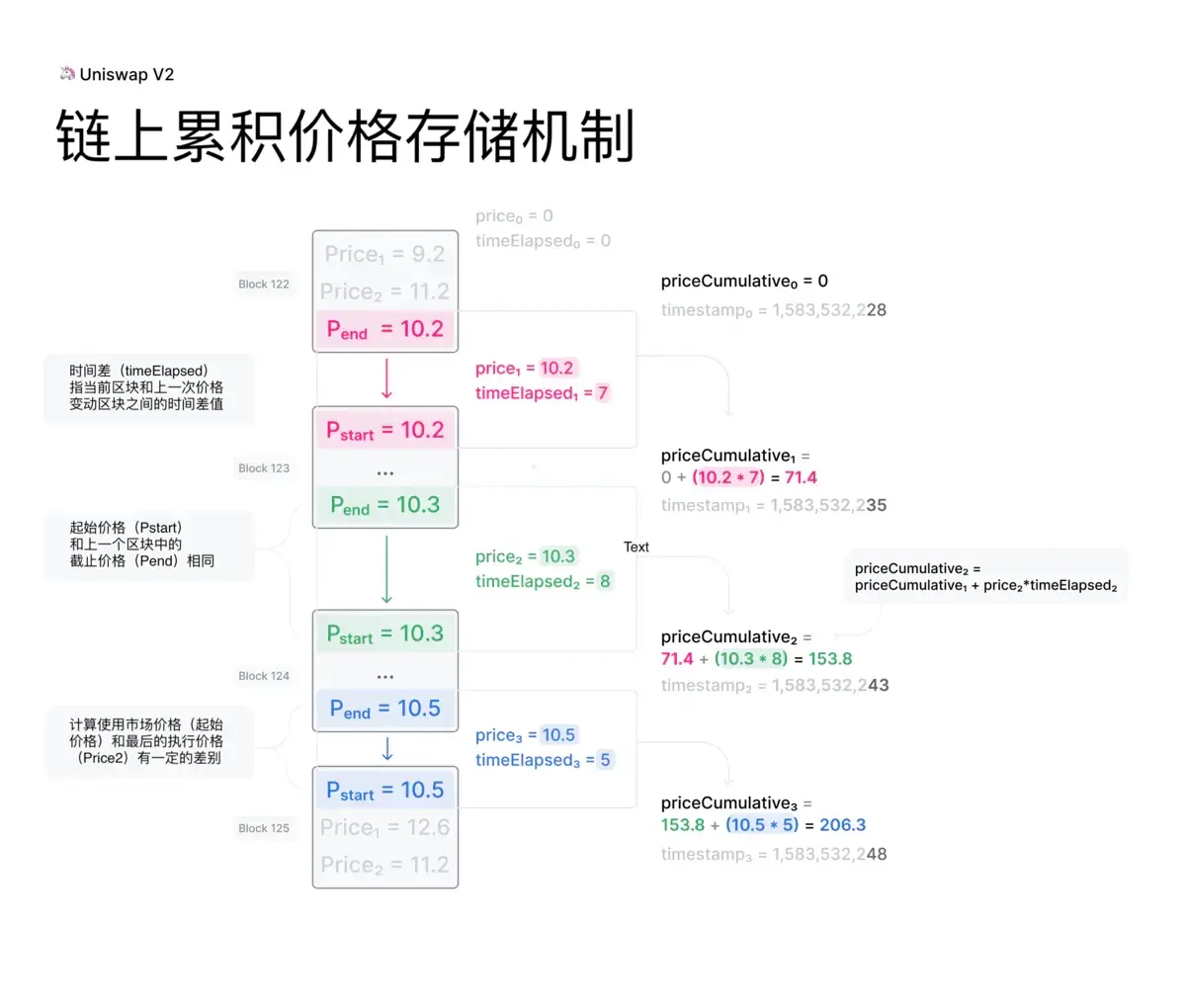
为什么 TWAP 必须跟踪两个价格比率

资产 A 相对于资产 B 的价格可以简单理解为 A / B 的比值，反之亦然。然而，在计算累积价格时，我们不能简单地通过“反转”一个价格比率来得到另一个。举个例子，假设价格累积的初始值为 2，并随后增加 3。如果试图通过取倒数来推导出另一个价格比率，结果将不正确：

$\frac{1}{2 + 3} \neq \frac{1}{2} + \frac{1}{3}$

这表明，两个价格比率需要各自独立累积，才能确保价格的精确跟踪。

固定时间窗口

固定时间窗口预言机的核心思想是通过两个时间点的累积价格快照来计算一段时间内的平均价格。具体做法是，先在某个时刻获取一次累积价格的快照，然后等待一段时间窗口（例如 24 小时），再获取一次累积价格。两次累积价格的差值除以这段时间的长度，就能得到这一时间段内的平均价格。

Uniswap 官方提供了一个使用案例，链接如下： ExampleOracleSimple.sol

案例中给出了怎么计算、保存和更新平均价格和平均价格的使用方式。

相信读者自行阅读代码能够理解，我们这里主要详细说下，UQ112x112 类型的平均价格的使用。再次建议先阅读我之前写的文章Solidity 中定点数的运算。

library FixedPoint {
    struct uq112x112 {
        uint224 _x;
    }

    struct uq144x112 {
        uint256 _x;
    }

    uint8 public constant RESOLUTION = 112;

    function mul(uq112x112 memory self, uint256 y) internal pure returns (uq144x112 memory) {
        uint256 z = 0;
        require(y == 0 || (z = self._x * y) / y == self._x, 'FixedPoint::mul: overflow');
        return uq144x112(z);
    }

    function decode144(uq144x112 memory self) internal pure returns (uint144) {
        return uint144(self._x >> RESOLUTION);
    }
}

import '@uniswap/lib/contracts/libraries/FixedPoint.sol';

contract ExampleOracleSimple {
    using FixedPoint for *;

    FixedPoint.uq112x112 public price0Average;
    FixedPoint.uq112x112 public price1Average;

    // note this will always return 0 before update has been called successfully for the first time.
    function consult(address token, uint amountIn) external view returns (uint amountOut) {
        if (token == token0) {
            amountOut = price0Average.mul(amountIn).decode144();
        } else {
            require(token == token1, 'ExampleOracleSimple: INVALID_TOKEN');
            amountOut = price1Average.mul(amountIn).decode144();
        }
    }
}

和 Uniswap V2 中保持一致，平均价格的保存类型为 uq112x112，在把数量和价格做乘法的时候，相当于一个整数乘以定点数，而我们知道整数乘以定点数是不需要额外计算操作的，直接相乘即可，只是此处 uq112x112 类型的整数部分会扩大转变成了 uq144x112 类型。最后进行 decode144() 操作，右移 112 位，去掉了 uq144x112 的小数部分，剩余的整数部分就是一个精度为 18 的定点数。

滑动时间窗口

Uniswap 提供的另一个示例是 ExampleSlidingWindowOracle.sol，这是一种利用滑动时间窗口计算平均价格的实现。

在这个合约中，只需要部署一个合约，就可以监控不同 pair 合约的累积价格。

首先，我们定义一个时间窗口大小 windowSize，例如 6 小时，这意味着我们获取的是过去 6 小时的平均价格。然后定义观测次数 granularity，例如 6 次，表示在 6 小时内进行 6 次观测。这样，每次观测的时间间隔 periodSize 就是 1 小时。

对于每个交易对，合约会维护 6 个 Observation 结构体，这些结构体依次更新，记录每次的价格快照。

    struct Observation {
        uint timestamp;
        uint price0Cumulative;
        uint price1Cumulative;
    }

通过 observationIndexOf() 函数，我们可以得到当前时间对应的 6 个观测点位中的对应的某个，也就是滑动窗口中的最新观测点。

getFirstObservationInWindow() 函数可以帮助我们找到当前滑动时间窗口中的第一个观测点。

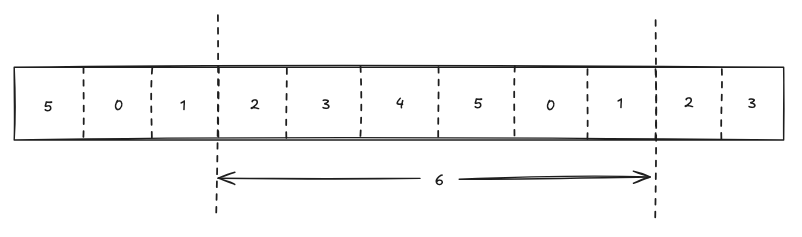
如上图所示，如果当前时间点对应的观测点处于区域 "1"，那么该时间窗口中的第一个观测点会处于区域 "2"。

update() 函数用于更新目前时间对应的观测点的 Observation 结构体。

最后，consult() 函数根据给定的代币数量，返回在当前平均价格下另一个代币的输出量。为了计算该输出量，合约首先使用 getFirstObservationInWindow() 函数获取当前时间窗口的第一个观测点的数据，并结合当前 pair 合约中的累积价格进行计算。

PriceCumulativeLast 会一直增加直到溢出，然后继续运行

Uniswap V2 是基于 Solidity 0.8.0 之前的版本构建的，因此在默认情况下，算术运算会发生溢出。在 0.8.0 之后的版本中，价格预言机需要使用 unchecked 代码块，以确保可以溢出。

当积累到一定程度，priceCumulativeLast 会溢出。当预言机计算价格变化时，结果将是一个负值。

然而，由于模运算规则，并不会产生影响。

为了简单说明，我们假设无符号整数的溢出点是 100。

当 priceCumulativeLast 为 80 时，我们做一个快照。在经过几笔交易/区块后，priceCumulativeLast 增加到了 110，但由于溢出，它变成了 10。此时我们用 10 减去 80，结果是 -70。但因为这个值是无符号整数，-70 mod 100 的结果是 30。这与没有溢出的情况的结果相同 (110 - 80 = 30)。

时间戳溢出

假设合约运行了几十上百年后，使用 uint32 来表示的时间戳，总有一天会溢出。但是和 priceCumulativeLast 一样，溢出是在预期中的，使用模运算，合约依旧能正常运行。为了简化，假设我们有一个在 100 溢出的时间戳。如果我们在时间 98 时做了快照，并且在时间为 4 时做了第二次快照，那么已经过去了 6 秒。(4 - 98) % 100 = 6，结果与预期一致。