Tornado Cash:开发者参考手册
- Krishang
- 发布于 2024-12-09 10:08
- 阅读 3184
Tornado Cash:开发者参考手册
- 原文链接:zk.bearblog.dev/tornado-cash...
- 译者:AI翻译官,校对:翻译小组
- 本文链接:learnblockchain.cn/article…
2024 年 12 月 02 日
本文由一位工程师爱好者撰写(嗨,我是 Krishang 👋🏽),献给同样是工程师和爱好者的你。
请在这个 tornado-cash-rebuilt 仓库中提出问题,以便指出任何代码问题。谢谢!
本文是对 零知识介绍 文章的后续内容。我们将详细介绍 Tornado Cash 的代码库。
我们的目标是让你了解整个开发周期,而不仅仅是 Solidity 智能合约。为此,我们将涵盖 [1] 架构概述, [2] Circom ZK 电路, [3] 智能合约以及 [4] 客户端的证明生成和验证(使用 Javascript)。
Tornado Cash 于 2019 年首次推出。自那时以来,ZK 工具的发展使得原始仓库有些过时。我们将通过 tornado-cash-rebuilt 仓库来重建 Tornado Cash,以现代的 Solidity 和 ZK 工具进行教育目的的重建。
概述
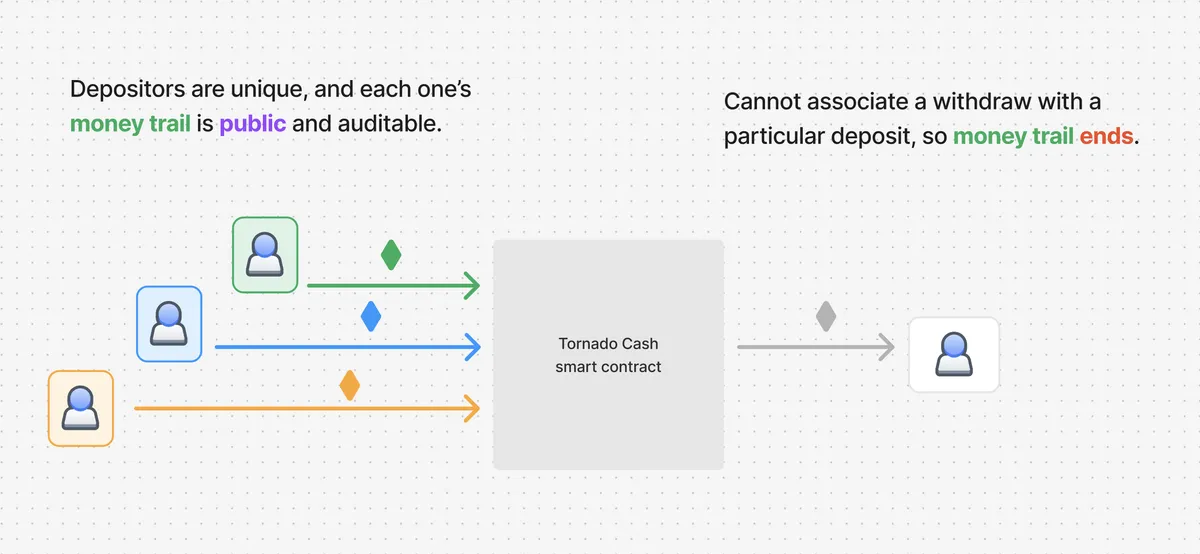
Tornado Cash 的目标是让一个账户(Alice)向其智能合约存入 1 以太,并允许另一个账户(Bob)提取 Alice 的存款,而不产生任何可识别的关联。
Tornado Cash 通过让存款人提交一个 commitment 以及他们的存款来实现此目标。这个承诺是两个值的哈希输出。
C=hash(n,s)
其中 C 被称为 commitment,n 和 s(nullifier 和 secret)是仅存款人所知的私有值。智能合约将仅在提取者证明他们知道 n 和 s 时,释放该存款金额给提取者。
为了证明这一点,如果提取者必须将 n 和 s(以直接或间接但可恢复的方式)暴露给智能合约,就可能在特定的存款和提取之间建立联系。这是因为我们可以从合约中所有存款中简单地查找承诺值 C,并检查哪个满足 C=hash(n,s)。
为了避免在存款和提取之间建立任何关联,Tornado Cash 使用零知识证明算法 Groth-16 来允许提取者证明他们对与特定存款相关的某些 n 和 s 的知识。
架构
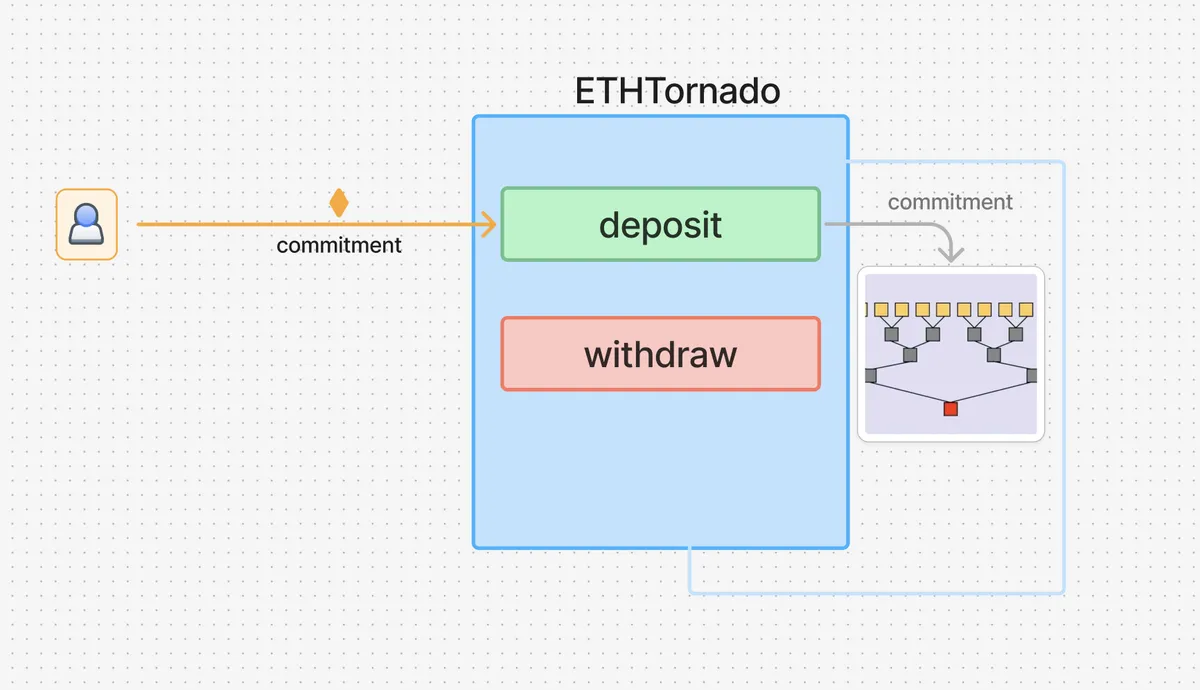
Tornado Cash 由两个智能合约 ETHTornado 和 Verifier 以及一个电路 Circuit 组成。
-
ETHTornado:用户通过此合约的deposit和withdraw函数进行交互。 -
Verifier:它的唯一目的就是验证为 Tornado Cash 电路生成的证明,并在每次提取时被调用。 -
Circuit:它在最开始时被用来生成Verifier智能合约。之后,每次提取时,提取者将私有值 nullifier n 和 secret s 作为输入提供给电路,并接收相关的零知识证明数据作为输出。
要向 Tornado Cash 存入 1 以太,存款钱包调用 ETHTornado 智能合约上的 deposit 函数,并发送一个合约存储在默克尔树中的 commitment。
要提取特定的存款,提取钱包调用 ETHTornado 智能合约上的 withdraw 函数。
为了防止在提取钱包和原始存款钱包之间创建可追溯的关联,合约要求提取者发送一个关于他们对与特定存款的承诺 C=hash(n,s) 相关的 nullifier n 和 secret s 的知识的 zero knowledge proof。
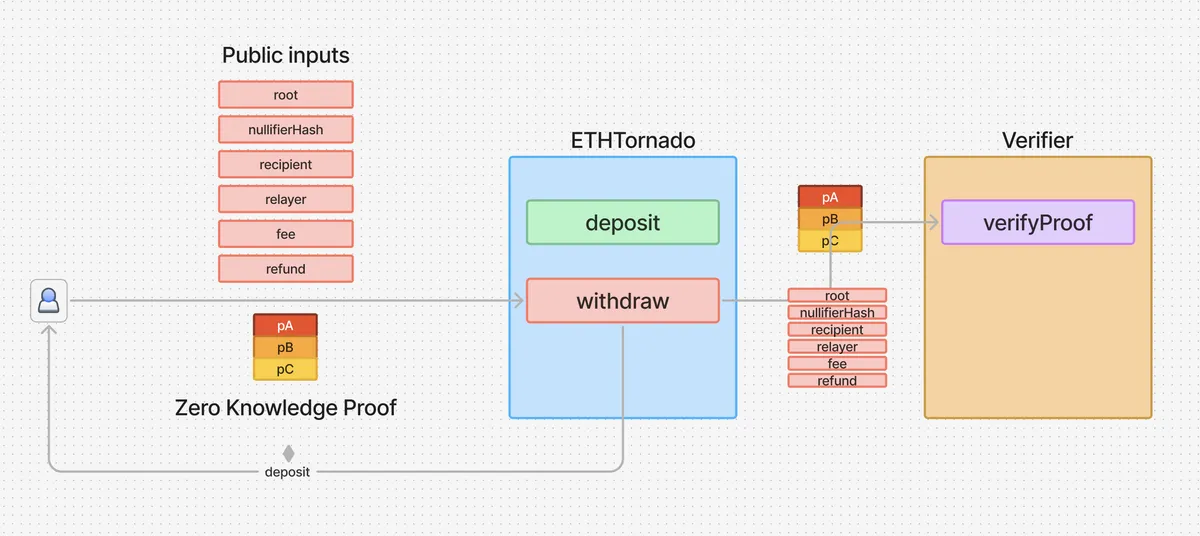
提取者将 [1] 证明和 [2] “公共输入” 发送到 withdraw 函数。这两个值都被发送到 Verifier 合约,如果提供的证明有问题,合约就会回退。
公共输入之所以称为公共,是因为提取者直接发送它们,没有任何加密或隐藏。
暴露这些输入对证明生成了重要的保证,而不妨碍零知识性质。例如,公共输入 recipient 是提取存款将要发送的地址。由于这个证明是以这个特定的 recipient 值作为输入生成的,因此没有人可以恶意地复制并在另一个提取交易中使用这个相同的证明,而该交易有一个不同的收件人地址。
提取者通过与 Circuit 交互生成关于他们对 nullifier n 和 secret s 的知识的零知识证明。
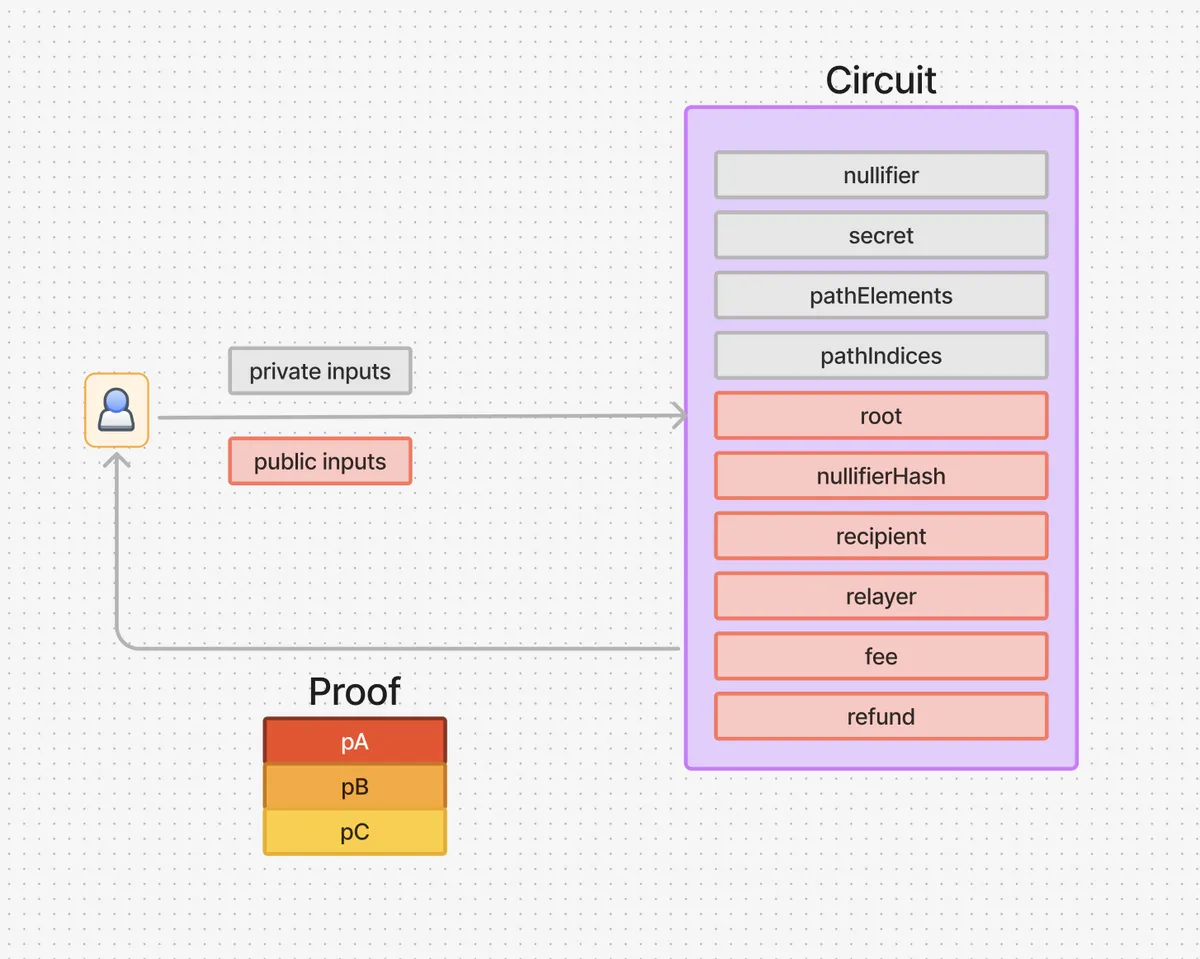
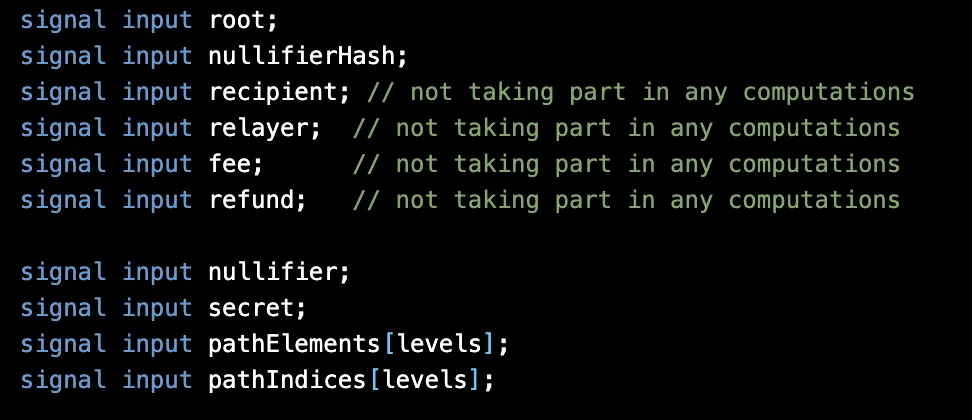
电路接受 [1] 公共输入和 [2] 私有输入。公共输入包括默克尔根 root,私有输入包括 nullifier、secret 和默克尔树路径元素。
电路对 nullifier 和 secret 进行哈希以计算出承诺,并使用这个承诺和路径元素,电路计算出一个默克尔根并检查它是否与公共输入 root 相同。
什么是默克尔树?
本节纯粹是自我满足。我只是想写一个简单、清晰且简短的默克尔树解释。
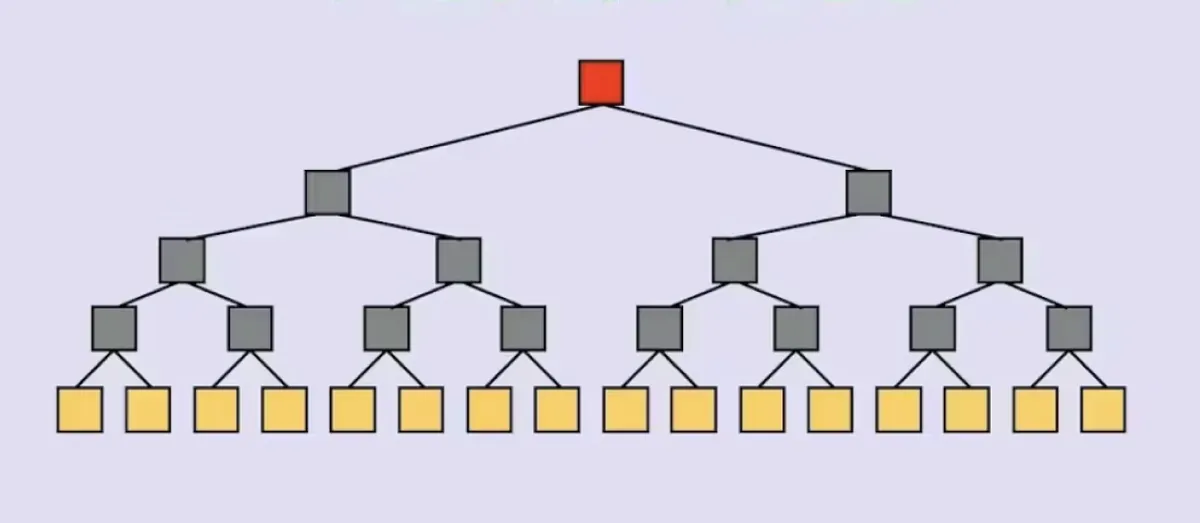
默克尔树是一种二叉树。它有一个根节点,根节点有两个子节点,每个子节点各有两个子节点,依此类推。
注意在根级别,树有 20^0=1 个节点。在Layer1,树有 2^1 个节点,在 Layer2 有 2^2 个节点 ... 在第 n 层,树有 2^n 个节点。
每个父节点是其两个子节点的哈希。因此,parent=hash(c1,c2)。这适用于所有节点,除了树的叶子节点(没有自身子节点的最底层节点)。
树的每个叶子是“原始数据”的一部分。如果一棵默克尔树有 n 层(不计算根作为层),这意味着它可以容纳 2^n 个原始数据。从这些叶子节点,可以构建整个默克尔树。
默克尔树的“超级能力”在于,如果树包含 2^n 个叶子,则只需 n 个数据即可证明某个数据是树的一个叶子。
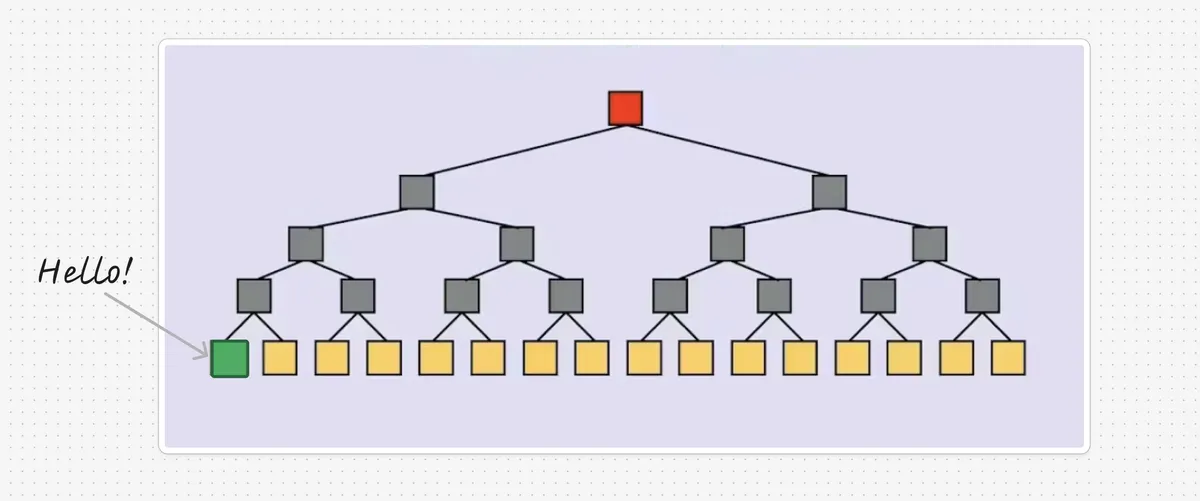
假设 Alice 有一棵包含 2^n 个叶子的默克尔树,其根为 R。Bob 有一段数据 d(图中的绿色节点),他想向 Alice 证明它是树的一个叶子。如果 Bob 将 d 发送给 Alice,而她盲目地将 d 与每个叶子进行比较,这会发生 2^n 次操作,这样做是非常麻烦的。
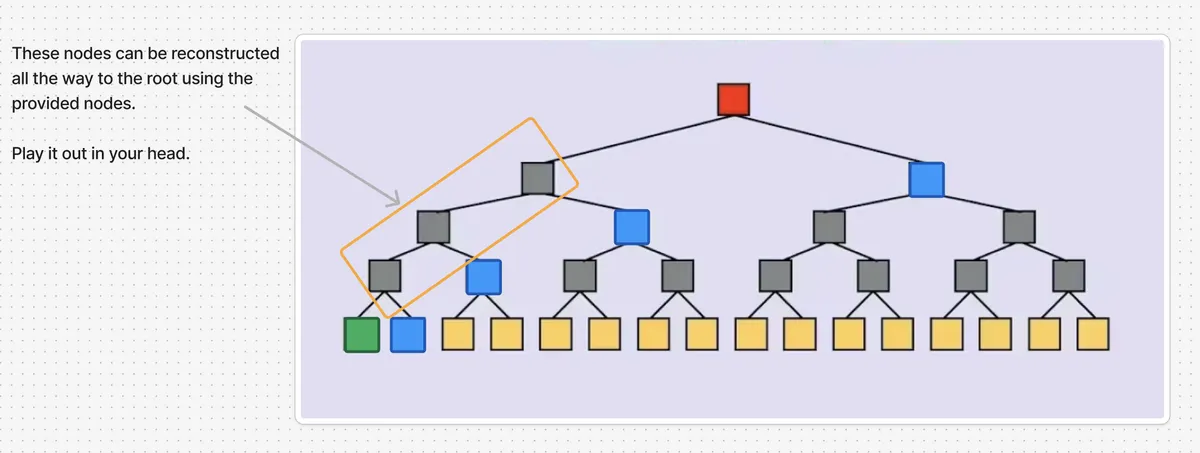
为了减少操作次数,Bob 将 d 与相关路径元素(即兄弟节点、父节点、祖父节点、曾祖父节点等树的节点,图中用蓝色标记)一起发送给 Alice。利用这 n 个节点,Alice 可以重建默克尔树根 R1,并检查它是否与她的默克尔树根 R 相同,以确定 d 是否是她的默克尔树的一个叶子。
代码
在本节中,我们将详细审查 Tornado Cash 背后的代码。我建议通过克隆 tornado-cash-rebuilt 仓库来跟随,并顺便给它一个星星。按照简单的 README 指示进行设置。
端到端流程
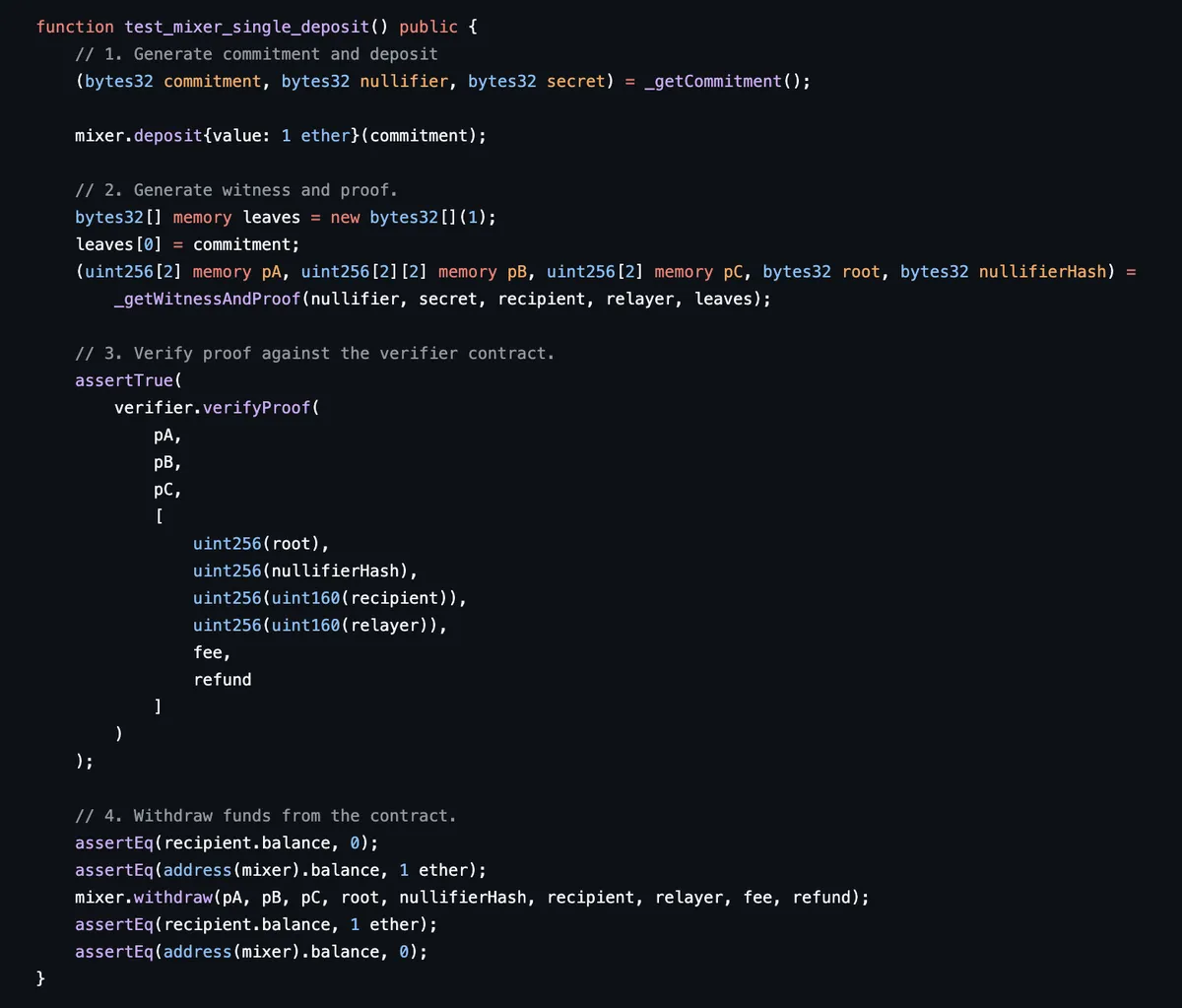
让我们首先查看 test_mixer_single_deposit 测试案例,以了解 Tornado Cash 的端到端流程。
在接下来的帖子中,我们将详细查看此测试案例的每个组件,以便对该端到端流程的内部运行有一个完整的低级理解。
-
我们生成两个随机的 bytes32 值
nullifier和secret。commitment只是这两个生成值的哈希。存入者调用deposit函数并传递承诺。 -
我们使用电路生成一个零知识证明(我们对 nullifier 和 secret 的知识)。
-
作为合理性检查,我们直接调用验证合约通过我们的证明来验证我们的证明是否合法。
-
提取者调用
withdraw函数并提供证明和公共输入以获取存款。
此测试本身应保证你 Tornado Cash 的存取款流程是一个类型化且具体的过程,我们可以逐步分解并完全理解。
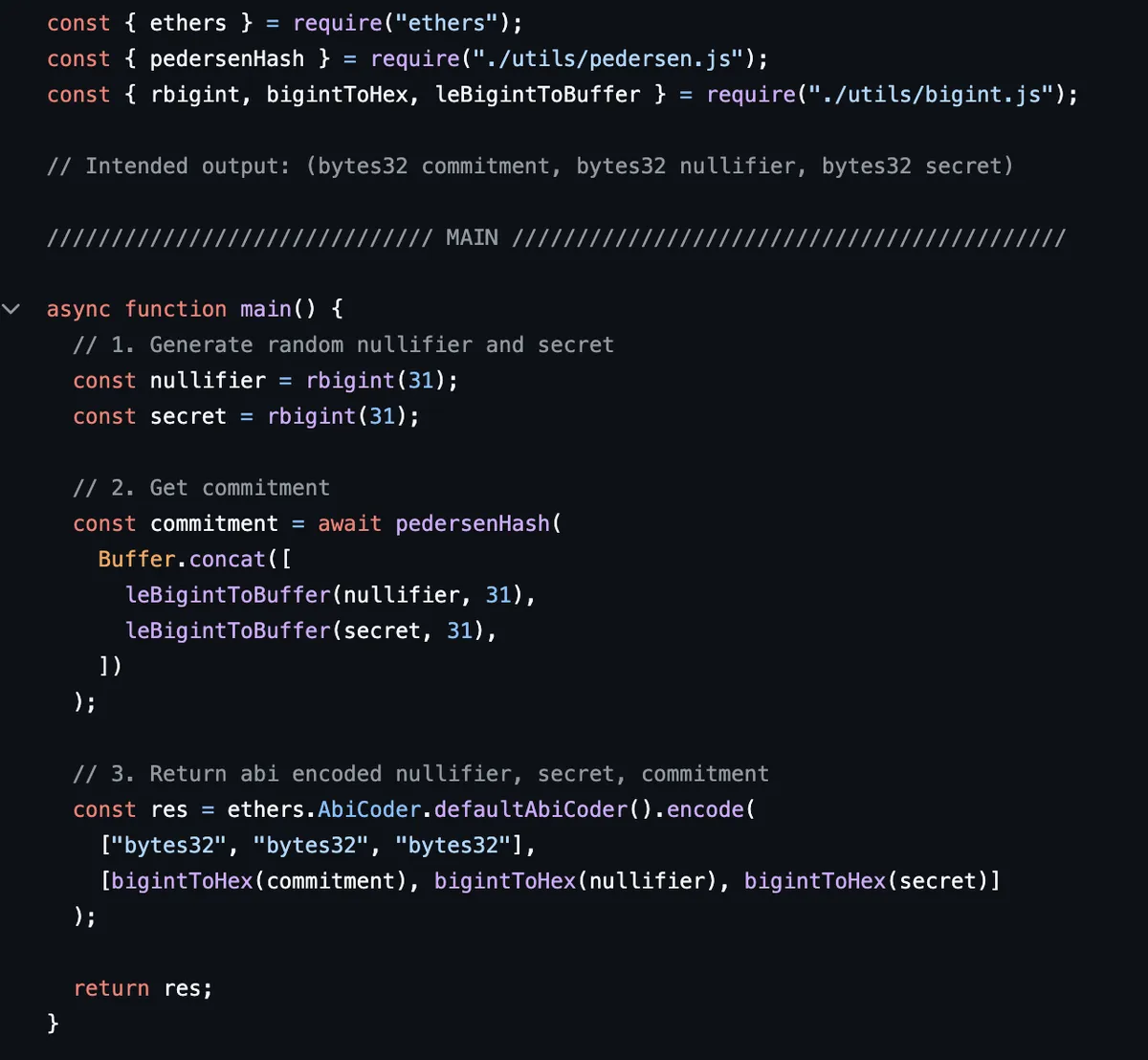
生成 nullifier 和 secret
步骤 [1] 中的 _generateCommitment 使用 forge vm.ffi API 调用 /forge-ffi-scripts/generateCommitment.js。
我们简单地生成两个随机数作为我们的 nullifier 和 secret,并将它们哈希在一起以创建我们的承诺。
pedersen 函数是一个哈希函数(就像 keccak256 是一个哈希函数),在零知识证明的上下文中效率很高。这意味着当我们在电路中使用它时,与其他哈希函数(例如 keccak 哈希函数)相比,它创建的算术约束较少。
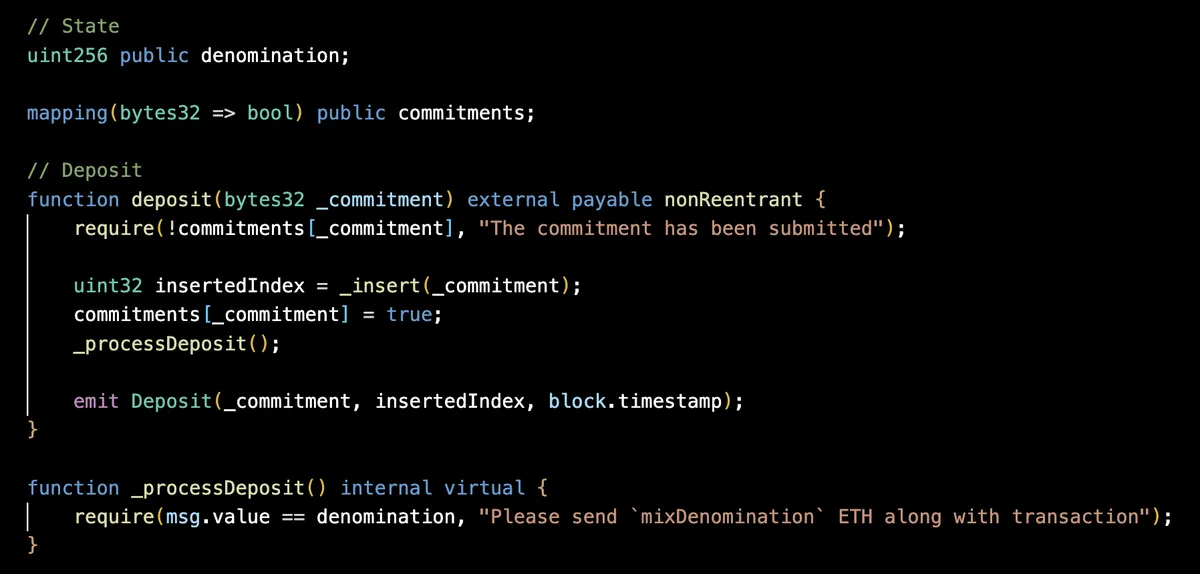
存入以太
存入者在 ETHTornado 合约上调用 deposit 函数 以存入以太。
合约将 commitment 标记为已使用,然后将其存储为默克尔树中的一个叶子,其 API 在 MerkleTreeWithHistory.sol 中定义。
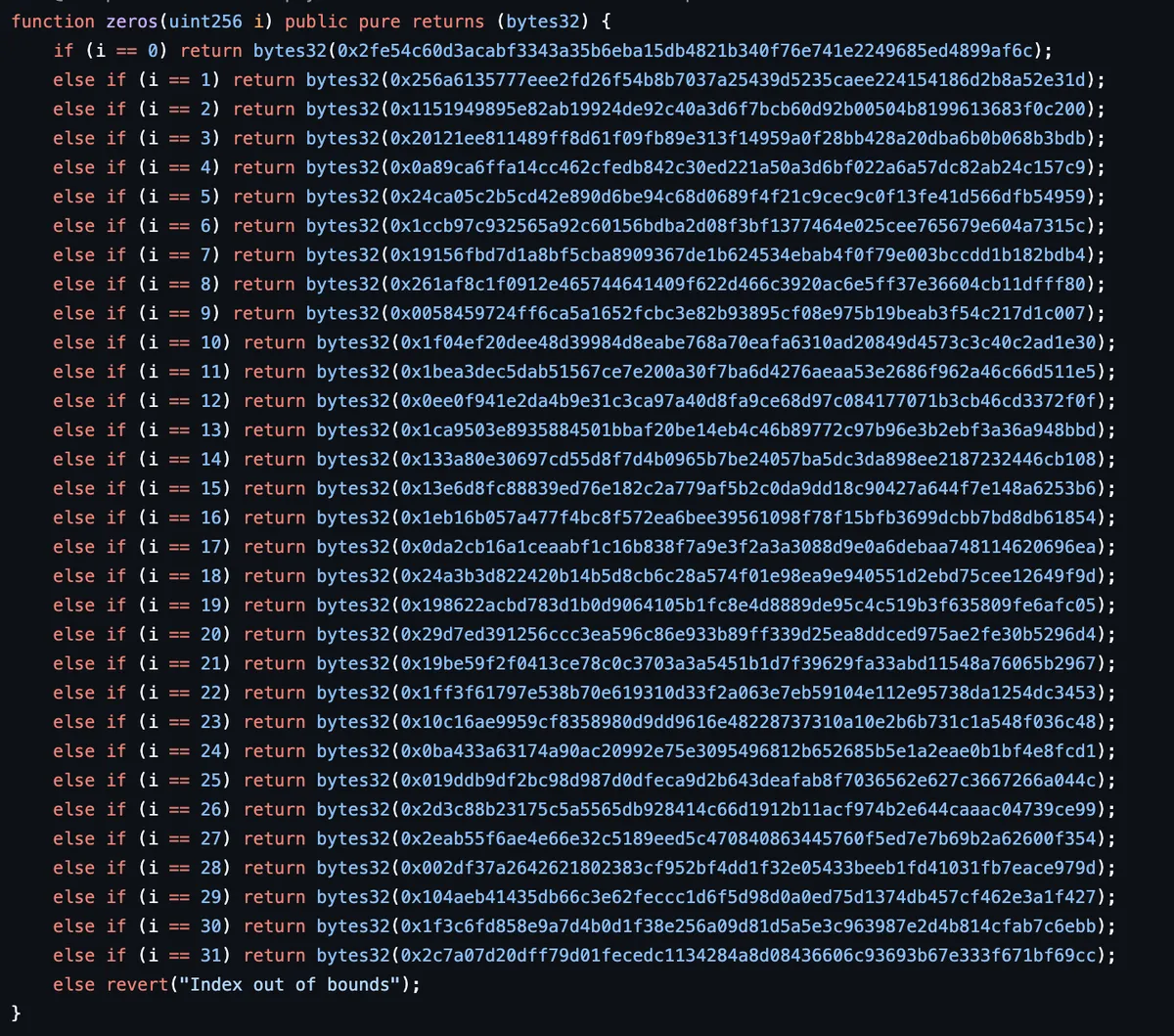
这是一个固定高度的默克尔树,并在每一层用 特定的零值 进行初始化。
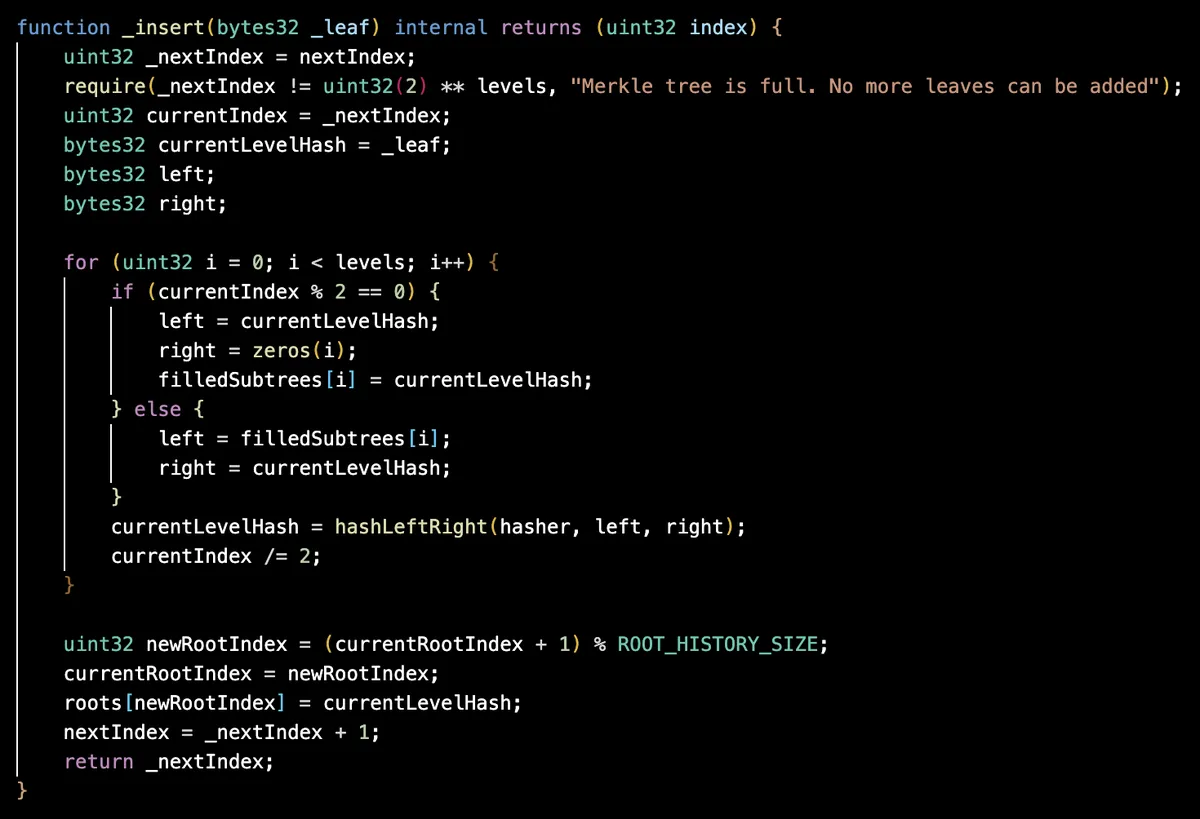
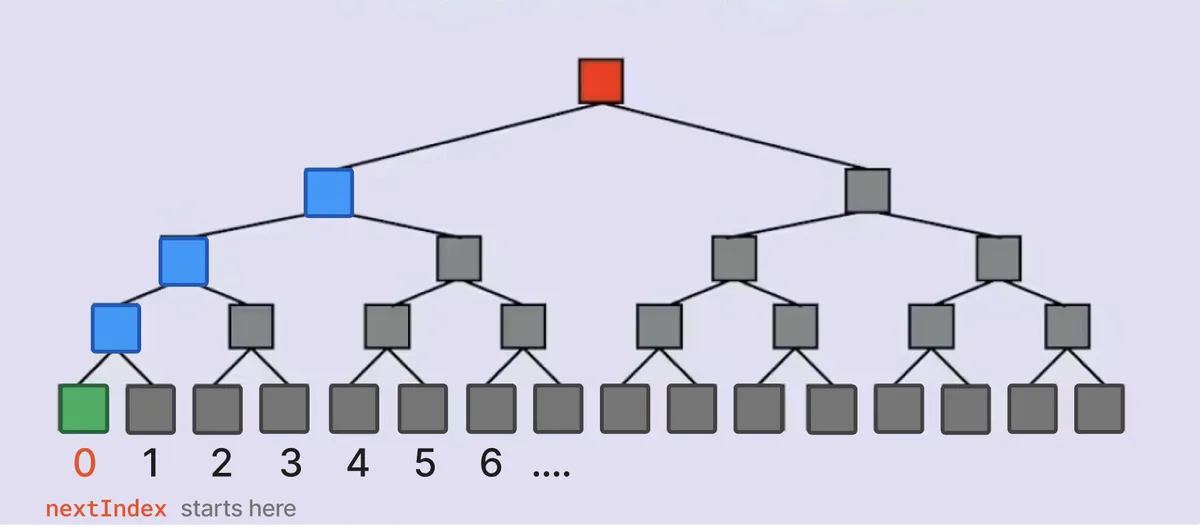
_insert 函数是一个用于从索引 0 到 2n 插入叶子到默克尔树并在每次插入时相应更新默克尔根的算法。
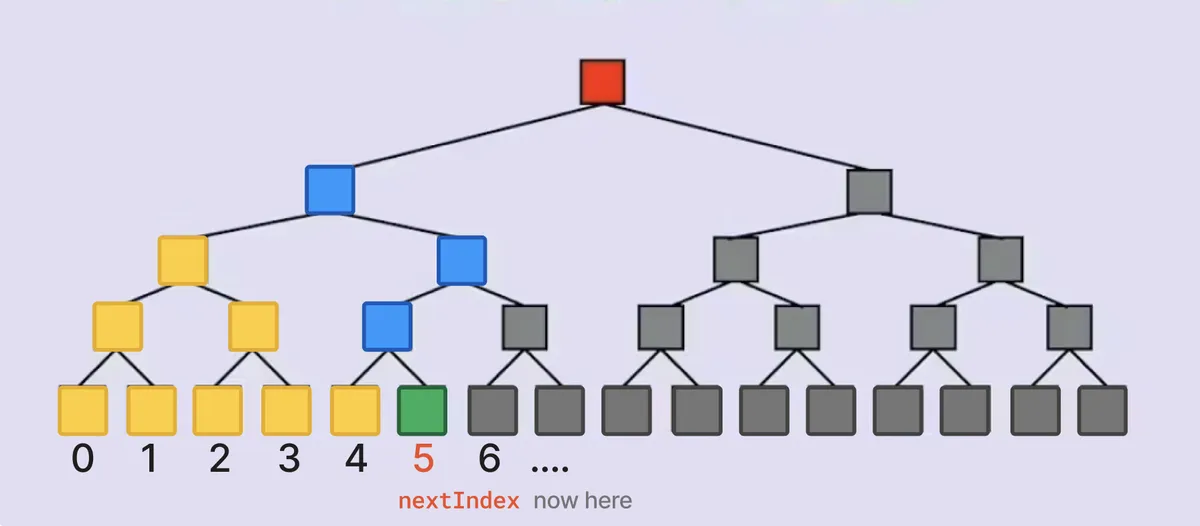
你可以像下图那样可视化插入操作。树的每个叶子都有索引。每层的灰色节点用该层的零值初始化。绿色节点表示我们在 nextIndex 处插入承诺的叶子,蓝色节点表示因此而更新的节点。黄色节点是先前插入中更新的非零节点。
最后,_processDeposit 调用确保所有存款金额相同,例如 1 个以太。这是因为如果某人存入确切的 0.30024 个以太,并使用另一个钱包提取相同金额,则存款和提取的金额在它们之间建立了关联,这是我们想要避免的。
生成证明 pA, pB, pC
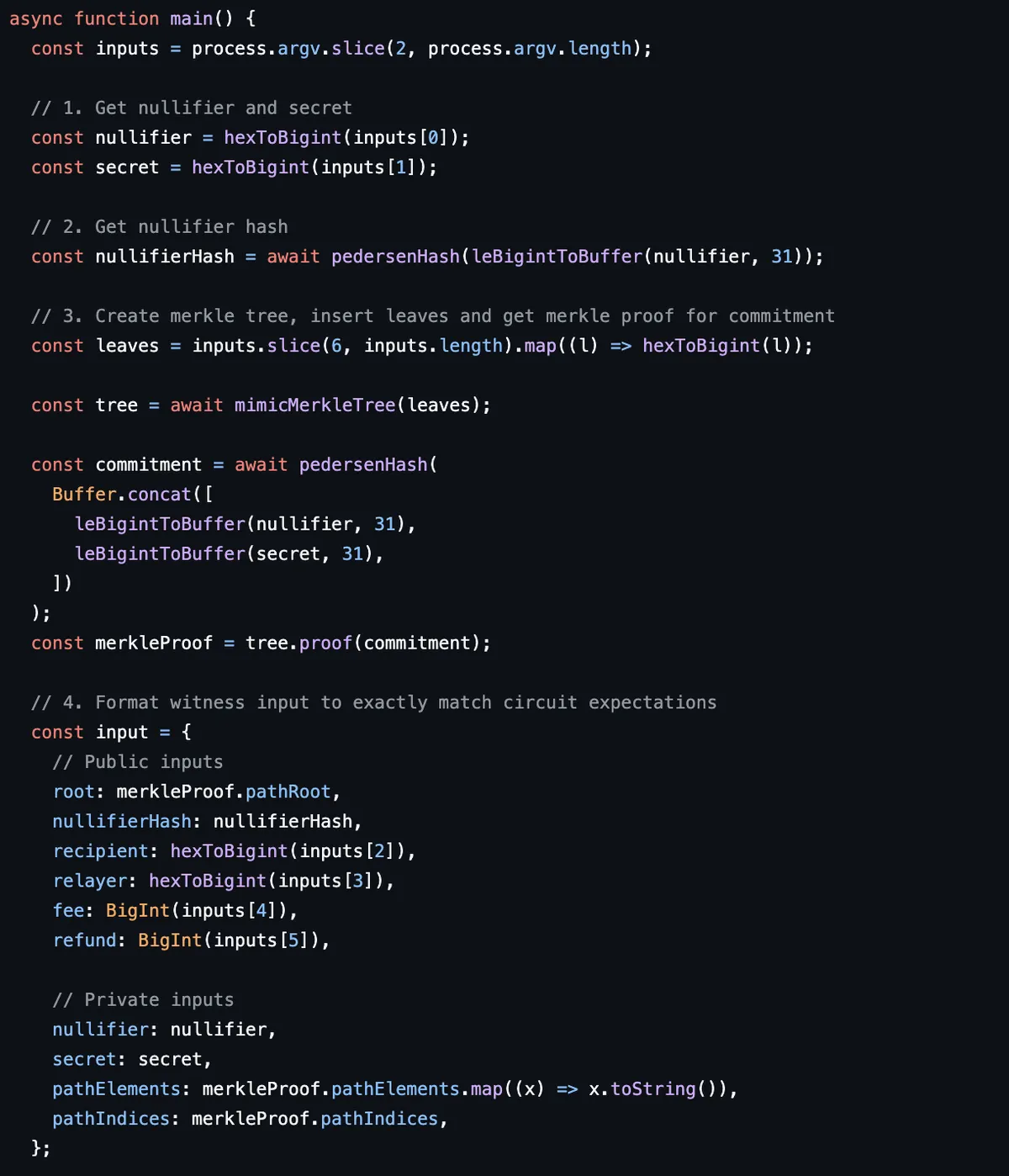
步骤 [2] 中的 _getWitnessAndProof 使用 forge vm.ffi API 调用 /forge-ffi-scripts/getWitness.js。
在这个脚本中,我们与电路进行交互以生成一个零知识证明。我们首先组装电路的输入(私有和公共)。
mimcMerkleTree 是 MerkleTreeWithHistory.sol 的 JavaScript 实现。默克尔树使用的哈希函数是 MiMC 哈希函数,这是另一个在零知识证明上下文中高效的哈希函数。
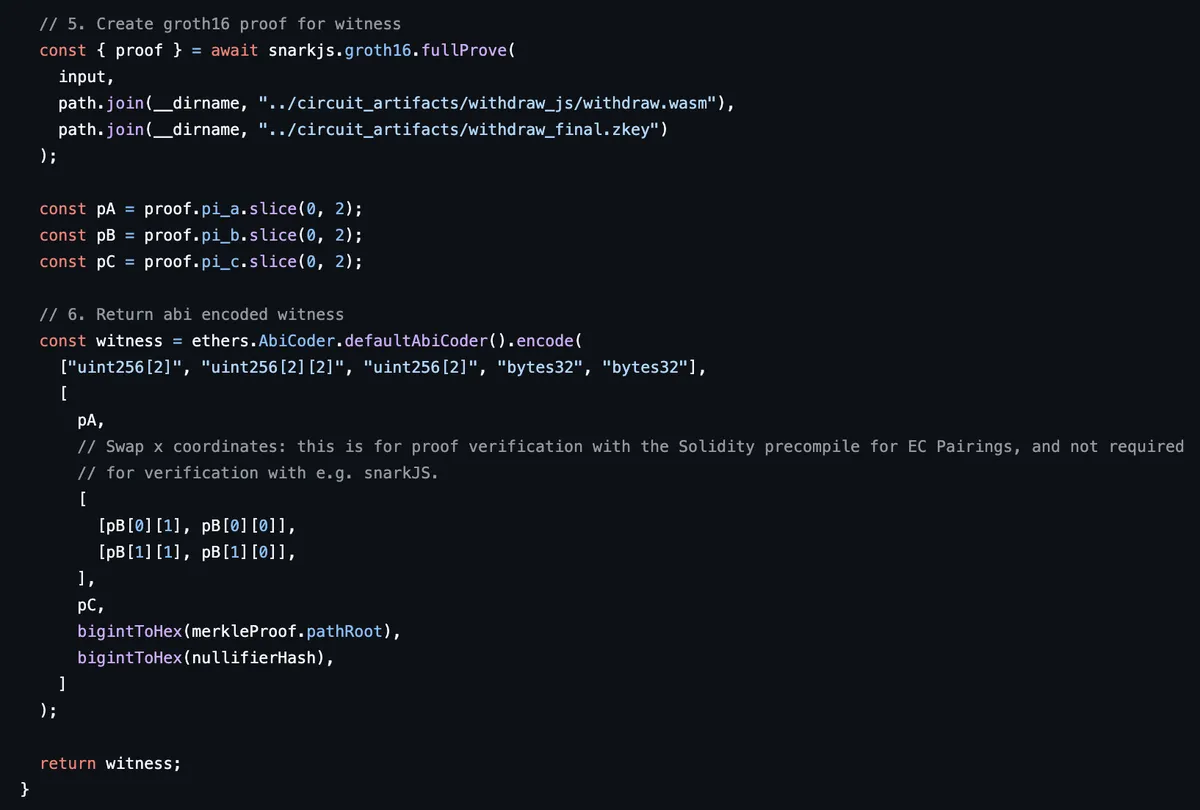
接下来,使用 snarkJS 库的 API,我们生成一个证明,并以所需格式返回。
Tornado Cash 电路:withdraw.circom 和 merkle.circom
“生成证明”或“与电路交互”等到底是什么意思?
本质上,电路接受输入并执行 assert 语句以检查输入是否满足某些条件。
Tornado Cash 的电路 接受以下输入:
电路首先断言:
hash( nullifier ) === nullifierHash
接下来,电路执行以下操作:
- 使用提供的 nullifier 和 secret 计算承诺
- 使用承诺和提供的路径元素计算默克尔根
- 最后,断言计算出的根和作为公共输入提供的根相同。
tree(commitment, path_elements).root === root
一旦你理解了这是电路的工作,阅读使用 Circom 编写的电路就不再是难事。
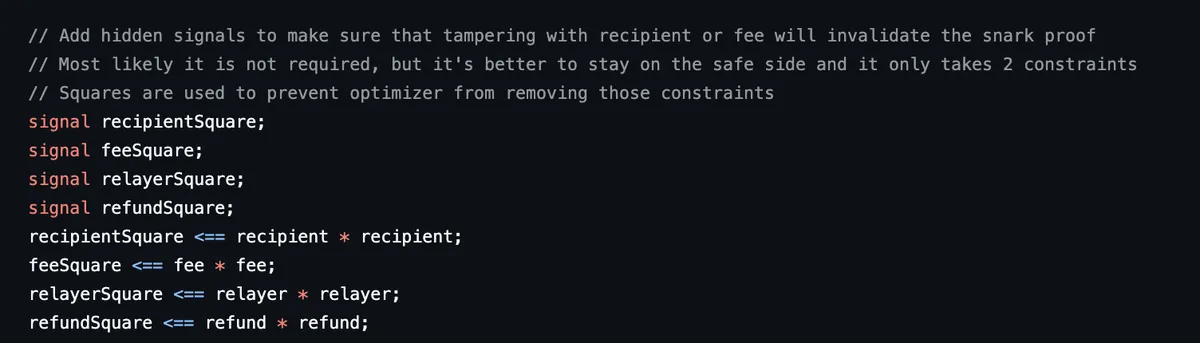
最后,你会注意到电路轻松使用了这些公共输入。
这些输入未参与上述的断言语句,但我们确实希望证明与这些输入严格相关。
举例来说,如果 Bob 以自己的钱包地址作为 recipient 生成了一个证明,我们并不希望恶意第三方能够简单地用自己的钱包地址重复使用 Bob 的证明。像这样的虚假断言:
(recipient * recipient) === (recipient * recipient)
确保为 Bob 的钱包作为收件人生成的证明只能与 Bob 的钱包作为 recipient 公共输入一起使用。
验证证明
一旦你克隆 tornado-cash-rebuilt,README 指示你运行 make all。
此设置说明涉及:
- 编译
/circuits中的 Tornado Cash 电路 - 本地提供熵(在“tau 庆典 ”中)
- 生成证明和验证密钥(你将在
/circuit_artifacts中找到) - 最后,生成
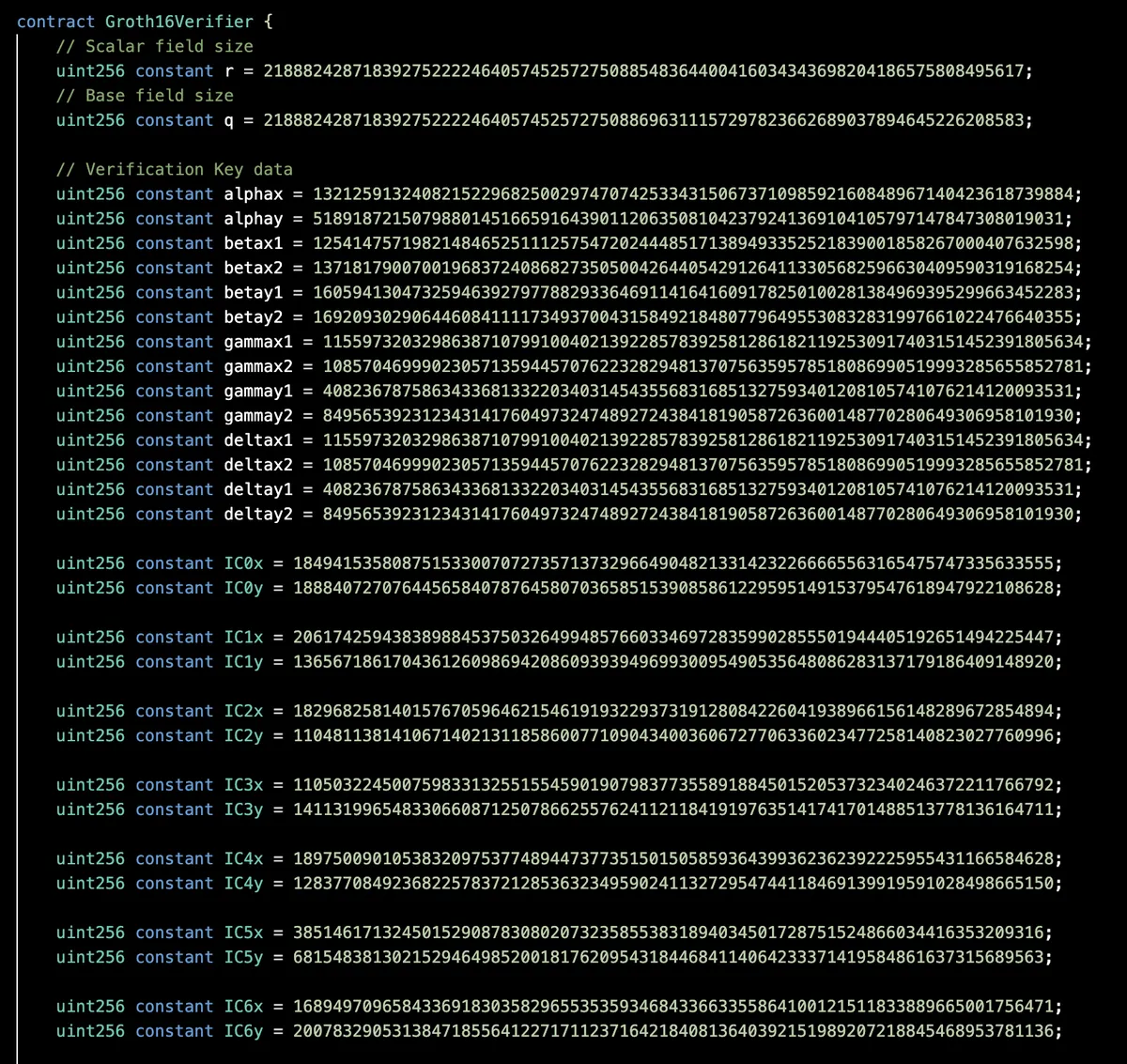
src/Verifier.sol合约。
该合约旨在验证我们为特定电路编译和生成证明/验证密钥的证明。
在我们的测试用例中,一旦生成了证明,我们通过直接调用 Verifier 合约的 verifyProof 函数来进行合理性检查,以检查我们是否生成了有效的证明。
我们以 pA、pB、pC 格式发送我们的证明,该格式是位于地址 0x08 的 Ethereum 预编译 所期望的。
// 在 `verifyProof` 中调用 0x08 的预编译
let success := staticcall(sub(gas(), 2000), 8, _pPairing, 768, _pPairing, 0x20)
关于证明生成和验证的数学和算法留待另一天讨论。(也许是下一篇文章?让我们拭目以待。)
提现资金
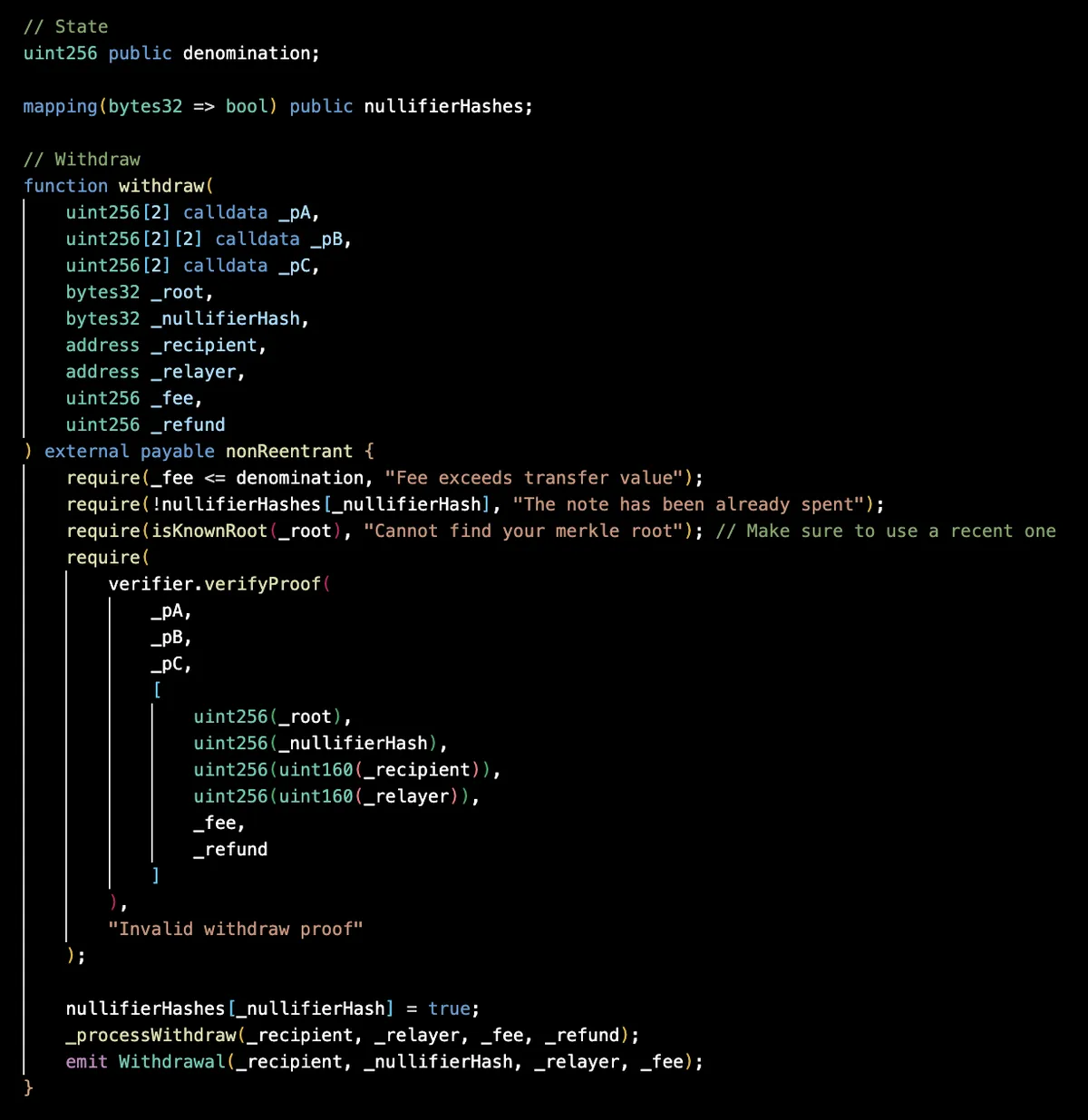
提取者在 ETHTornado 合约上调用 withdraw 函数 以提取特定存款。
合约通过确保 nullifierHash 未被使用来确保证明未被重放。然后,它确保提供的公共输入 root 是其默克尔树的(当前或过去 30 个)根之一,通过 isKnownRoot 进行验证。
最后,合约调用 Verifier 来验证提供的证明和公共输入。如果验证成功,合约将 nullifierHash 标记为已使用,并将存款释放到提供的接收地址。
就这些!
我们已经介绍了使用 Tornado Cash 的完整端到端流程中涉及的所有相关代码——从电路到合约和客户端代码。
这篇文章没有涵盖 Groth-16 零知识证明算法背后的数学,因此证明生成和验证的 如何 仍然可能对你来说是一个黑盒。这没关系。例如,你可能不知道哈希函数是如何工作的,但你仍然在使用它们。(当然,我不是发明这个比喻的人。)
如果你对本文中提到的 Tornado Cash 有任何问题或疑问,或想提出任何更正,请在 tornado-cash-rebuilt 仓库中提出问题,或在推特上 DM 我 @MonkeyMeaning。
- 翻译
- 学分: 77
- 分类: 零知识证明
- 标签: Tornado.cash Tornado
- 【视频】Tornado Cash 代码实践系列 3023 浏览
- 尝试用 Halo2 实现 Tornado Cash 4044 浏览
- 实现链上隐私的不同方法 3505 浏览
- SharkTeam:Tornado.Cash提案攻击原理分析 4652 浏览
- Tornado.cash: 一个关于匿名和zk-SNARKs的故事 6553 浏览
- 零知识证明-Mixer(混币)应用分析 14611 浏览