Diffie-Hellman问题、ECDH密钥交换和ElGamal加密协议

Diffie-Hellman 问题、ECDH 密钥交换和 ElGamal 加密协议。

在密码学中，Diffie-Hellman 问题在许多高级密码协议中发挥了关键作用。可以将它们视为密码学中的 公理。在深入研究数字签名方案等复杂的密码协议之前，我认为了解这些 公理 及其应用是值得的。在本文中，我旨在详细阐述 Diffie-Hellman 问题及其最重要的应用——椭圆曲线 Diffie-Hellman（ECDH）密钥交换和 ElGamal 加密协议。我希望这篇文章以及我之前关于 “高级密码学原语” 的文章能为进一步研究高级密码学奠定基础。让我们开始吧！

Diffie-Hellman 问题

与 Diffie-Hellman 相关的主要问题有三个，每个问题具有不同的难度和对密码安全性的影响：

离散对数问题 (DLP)

• 定义：给定一个素数 p、一个生成元 g（在 模 p 的乘法群 中），以及群中的一个元素 h，离散对数问题是找到整数 x，使得：

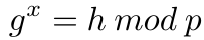
离散对数问题。

• 难度：DLP 被认为是困难的，这意味着目前没有已知的有效算法可以在一般情况下解决它，特别是在大素数的情况下。

计算 Diffie-Hellman 问题 (CDHP)

• 定义：给定一个素数 p、一个生成元 g 和两个元素 g^a 和 g^b（其中 a 和 b 是未知的），CDHP 是计算 g^ab。
• 与 DLP 的关系：解决 DLP 将允许解决 CDHP，但反之不一定成立。如果 DLP 是困难的，则假定 CDHP 也是困难的。

决策 Diffie-Hellman 问题 (DDHP)

• 定义：给定一个素数 p、一个生成元 g 和三个元素 g^a、g^b 和 g^c，DDHP 是判断是否 c = ab mod p。
• 安全影响：DDHP 用于确保对手无法区分真实的 Diffie-Hellman 交换和随机值。通常它被认为比 CDHP 更容易。

需要注意的是，上述问题被假定为困难，因此也称为 Diffie-Hellman 假设。然而，最近的 配对操作 已证明 DDHP 是易于解决的，而 CDHP 和 DLP 仍假定为困难。

Diffie-Hellman 问题是许多高级密码协议安全性的重要基础，尤其是数字签名方案。因为它们是一些假设，我喜欢将它们视为密码学的 公理。现在让我们探索这些 公理 的一个重要应用。

ECDH 密钥交换协议

椭圆曲线 Diffie-Hellman（ECDH）密钥交换协议用于在两方之间安全地交换加密密钥。一旦密钥成功且安全地交换，双方可以使用该密钥通过对称加密算法（如 AES）对发送的消息进行加密。通过利用椭圆曲线密码学中的 Diffie-Hellman 问题，两方之间的通信变得安全。然而，在深入协议之前，让我们在椭圆曲线的上下文中重申 Diffie-Hellman 问题。

椭圆曲线 Diffie-Hellman (ECDH) 问题

• 离散对数问题 (DLP)

给定在有限域 F_q 上的椭圆曲线 E 的点 X，生成元 G，在有限域 F_q 中寻找数字 x 是困难的，使得：

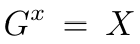
椭圆曲线上的 DLP

换句话说：

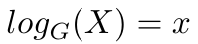
以对数形式表示的 DLP

• 计算 Diffie-Hellman 问题 (CDHP)

给定在有限域 F_q 上的椭圆曲线 E 的两个点 G^a 和 G^b，生成元 G，a 和 b 是有限域 F_q 中的未知数字，寻找点 G^ab 是困难的。

• 决策 Diffie-Hellman 问题 (DDHP)

给定在有限域 F_q 上的椭圆曲线 E 的两个点 G^a 和 G^b，生成元 G，a 和 b 是有限域 F_q 中的未知数字，区分 G^ab 和曲线上的随机点是困难的。

密钥交换协议

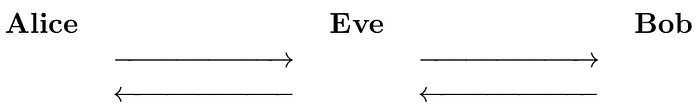
不安全通信上的密钥交换。

假设 Alice 想与 Bob 以安全的方式进行交流，以便 Eve（一个窃听者）无法理解 Alice 和 Bob 之间的消息。可以按照以下方式使用 ECDH 实现密钥交换协议：

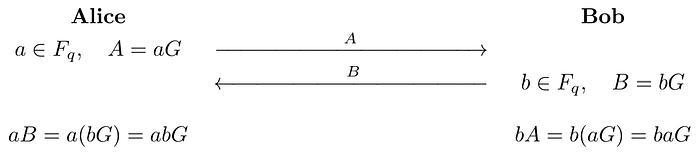
ECDH 密钥交换协议。

假设 Alice 和 Bob 预先达成协议，将使用某标准椭圆曲线 E，在有限域 F_q 上，生成元 G。Alice 从有限域 F_q 中生成一个随机私钥 a，计算她的公钥 A = aG 并将 A 发送给 Bob。Bob 也从有限域 F_q 中生成一个随机私钥 b，计算他的公钥 B = bG 并将 B 发送给 Alice。现在，Alice 计算 aB = a(bG) = abG，Bob 计算 bA = b(aG) = baG。我们注意到，Alice 和 Bob 计算出相同的结果 abG，而这就是他们可以用于加密消息的共享密钥。

安全分析

ECDH 密钥交换协议的安全性依赖于离散对数问题 (DLP) 和计算 Diffie-Hellman 问题 (CDHP)，这两者在椭圆曲线上都被认为是困难的。在 Alice 和 Bob 之间的通信中，Eve 仅知道公钥 A 和 B。根据 DLP，Eve 无法确定私钥 a 和 b。此外，根据 CDHP，Eve 也无法确定共享秘密 abG。因此，协议被证明是安全的。

主动攻击者与缓解

在前面的部分中，我们假设 Eve 被动窃听 Alice 和 Bob 之间的通信，因此无法确定秘密密钥。让我们改变这种情况；假设 Eve 主动干扰通信并冒充对方；即她冒充 Bob 对 Alice 和冒充 Alice 对 Bob。该攻击在下图中进行了说明。

类似主动攻击的示意图。

在这种攻击中，Eve 将 Alice 的公钥 A 发送给 Bob。类似地，Eve 将 Bob 的公钥 B 发送给 Alice。最终，Eve 与 Alice 建立了共享密钥 aeG，与 Bob 建立了共享密钥 beG。也就是说，Eve 可以解密来自 Alice 或 Bob 的 ciphertext。根本问题在于，Alice（或 Bob）在接收到另一方的公钥时，她（或他）无法知道公钥实际上来自对方。

为了缓解这一攻击，Alice 和 Bob 使用数字签名对他们的 ECDH 公钥 A 和 B 进行签名。

主动攻击缓解。

由于 Eve 无法代表 Alice 或 Bob 生成有效的签名，上述攻击将不再有效。

代码示例

以下是 ECDH 密钥交换的代码示例。

signature-schemes/ecdh/ecdh_key_exchange.py a

ElGamal 加密协议

ECDH 密钥交换的一个重要应用是 ElGamal 加密。基本思想是使用 ECDH 建立共享秘密并使用共享秘密来掩盖消息。

ElGamal 加密协议。

为了加密消息 m，我们创建一个在 E 上的点 P_m(x,y)，其 x 坐标为 m。当 Bob 收到 Alice 的公钥 A 时，他并不如在 ECDH 密钥交换中那样将他的公钥 B 发送给 Alice，而是发送 B 和 bA + P_m 给 Alice，即 (c1, c2) = (B, bA + P_m)。当 Alice 接收到 (c1, c2) 时，她计算：

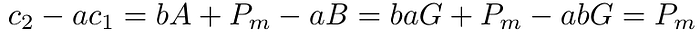
消息 m 是点 P_m 的 x 坐标。以下是代码示例。

signature-schemes/ecdh/elgamal.py

结论

尽管自 1976 年以来已发布，Diffie-Hellman 问题及其简单应用，如 ECDH 密钥交换和 ElGamal 加密，仍然是许多现代高级密码协议安全性的基础。然而，随着最近在密码学中的发展，如配对操作，其中一些问题已被攻破，特别是决策 Diffie-Hellman 问题 (DDHP)。在我看来，深入理解 Diffie-Hellman 问题的优缺点对于设计更安全的密码协议至关重要。在接下来的文章中，我们将深入研究更高级的协议，从数字签名开始。敬请关注！

如果你觉得这篇文章有启发，请关注我。这将让我非常开心，并激励我写更多高质量的文章。非常感谢你的支持 🙏

参考文献

1. 0xbarchitect — 高级密码学原语
2. Nguyen Thoi Minh Quan — 直观的高级密码学
3. 维基百科 — Diffie-Hellman 问题
4. Philipp Muens — 椭圆曲线 Diffie-Hellman
5. Andrea Corbellini — 我们能否使用椭圆曲线加密数据？
6. 维基百科 — ElGamal 加密

• 原文链接： medium.com/@barchitect/d...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～