Noir 的电路后端
- jtriley
- 发布于 2024-12-23 15:24
- 阅读 1783
Noir编程语言提供了一种熟悉的Rust风格的接口,用于编写自定义zk-SNARK程序。文章详细介绍了Noir编译器的工作原理,如何生成算术电路和适用于Aztec网络的智能合约字节码,并探讨了PLONK和其变体的约束系统。通过对电路的有效性和计算成本的思考,展示如何在使用Noir编写程序时优化电路性能。
引言
Noir 编程语言允许使用熟悉的、类 Rust 的接口来编写自定义 zk-SNARK 程序。
zk-SNARK 的灵活性使得几乎图灵完备的程序可以被证明一次,并以亚线性时间复杂度进行验证,且证明者与 verifier 之间没有交互。开发这些程序(也称为电路)通常很具挑战性,因为程序必须还原为一系列算术约束。由此,产生了两种不同的策略,一种使用 zk-SNARK 特定领域语言(DSL),依赖编译器将程序转换为可以被证明和验证的约束,而另一种则使用 zk-SNARK 虚拟机(zkVM)电路,该电路可以处理指令,然后证明和验证其执行轨迹。
历史上,zk-SNARK 的 DSL 由于其非常规的语法和编程范式而较为困难,尽管生成的电路能够比 zkVM 更快地被证明。zkVM 模型最成功地依赖于 RISC-V 等机器架构,因其精简的指令集、开放的规范以及作为 LLVM(和使用 LLVM 的语言)目标的支持。尽管历史上证明 zkVM 的速度要慢得多,但在写作时,证明性能已有了显著提高。
Noir 是前一种策略的近期补充,它将源代码编译成中间表示,该表示可以根据需要转换为适当的 zk-SNARK 后端。在写作时,Noir 将 UltraHonk 作为电路的目标,将 MegaHonk 作为 Aztec 网络上私有智能合约的目标。
Noir 编译器
Noir 并不直接证明电路,也并不完全合成约束系统。相反,Noir 可用于两个目的,要么生成算术电路,要么为 Aztec 虚拟机(AVM)生成智能合约字节码。出于本文的范围,我们将专注于前者,它用于可以在链外被证明,链外或链上可由自动生成的 Solidity 验证器验证,该验证器可以部署到以太坊虚拟机(EVM)上。
算术电路
Noir 编译器的输出不是电路本身,而是字节码。该字节码由算术电路虚拟机(ACVM)解释,它生成最终约束系统下的电路。这作为编译目标非常重要,因为这允许 Noir 输出指向任意的约束系统。由 ACVM 解释的字节码可分为两类,即算术电路中间表示(ACIR)字节码和 Brillig 字节码。ACIR 的操作码对应于最终电路中的约束,而 Brillig 的操作码对应于不受约束的计算。ACIR 操作码可以调用 Brillig 函数,但反之则不行。
在受限的 SNARK 中,一些计算的执行代价很高,尽管检查其正确性可能要便宜得多。因此,我们可以在 Brillig 函数中定义 SNARK 不友好的计算,从 ACIR 中调用这些函数,并在之后对 Brillig 函数的输出进行约束以确保正确性。
例如,电路中的除法是在域元素上执行的,要求使用一种昂贵的算法(通常是扩展欧几里得算法)来查找乘法逆元。我们可以将搜索的任务委派给 Brillig 函数,而不是在电路中查找逆元。Brillig 函数 应该 返回乘法逆元,但需要注意的是,在不受约束的环境中,恶意的证明者可能返回错误的值。因此,我们按如下方式约束该函数的输出。
fn div(x: Field, y: Field) -> Field {
let inv_y = unsafe { inverse(y) };
assert_eq(1, y * inv_y);
x * inv_y
}
unconstrained inverse(x: Field) -> Field {
// 扩展欧几里得算法
// -- 省略
}利用 n * inverse(n) == 1 的乘法逆元法则,我们可以通过一次乘法等式检查来约束 Brillig inverse 函数的输出是否正确,这对于算术电路而言是相当便宜的。
PLONK 的简史
关于耶稣会的非常非交互式知识证明的排列,即 PLONK,是第一种 PLONK 类 zk-SNARKs。PLONK 是 Groth16 的一次迭代,无论是在承诺方案还是约束系统上。特别是,约束系统被扩展以规定更复杂的代数逻辑。
TurboPLONK 通过添加任意自定义门扩展了 PLONK,也就是说,约束系统可以从 PLONK 扩展以容纳自定义逻辑;尤其是,TurboPLONK 添加了椭圆曲线点算术所需的约束。然而,TurboPLONK 已被 UltraPLONK 超越。
UltraPLONK 通过添加查找表扩展了 TurboPLONK,正式称为 Plookup。这使得查找表以高效可证明和可验证的方式替代更昂贵的 SNARK 不友好的约束。随着时间的推移,UltraPLONK 得到了改进,以封装自定义门和查找表。
Aztec 的 HONK 和类似的 EspressoSystems 的 HyperPLONK,通过改变约束系统插值到多项式的方式,显著提高了 PLONK 类证明生成的效率。对于应用开发者来说,这并不直接实用,但其名称在实际应用中会被频繁提及,因此进行了相应的解释。
Noir 将 UltraHONK 作为其电路后端,也就是说,它以具有自定义门、查找表的 PLONK 类约束系统为目标,并采用可在亚线性时间复杂度上进行证明的多元多项式承诺方案。
约束系统
约束系统的核心是构建输入向量(也称为见证)和电路矩阵,这些矩阵变换见证,从而可以检查正确性。承诺方案通常涉及将这些矩阵转换为多项式向量,以便所有相同的算术规则仍然适用,而且多项式可以在单个评估点上进行检查,而无需检查矩阵的每个元素。多项式插值超出了本文的范围,但我们将以 Groth16 约束系统作为 PLONK 约束系统的基础。
Rank 1 约束系统
Rank 1 约束系统,也称为 R1CS,是 Groth16 的约束系统,它是 PLONK 的著名前身。R1CS 要求电路是系列的 n 个等式约束 a * b = c。
$$
a1⋅b1=c1 \
a2⋅b2=c2 \
⋯ \
an⋅bn=cn
$$
给定这系列约束,我们推导出一组输入 i,输出 o,中间值 m,以及一个常量值 1,这个常量值俗称见证向量 w。
注意:常量项 1 可以在电路中乘以常数时使用,并非总是必要,也并不总是 1,但仍然包括在内。
$$ w→= [1i0⋯o0⋯m0⋯] $$
此外,我们将系列约束转换为维度为 m*n 的 'A'、'B' 和 'C' 矩阵,分别对应于约束数量和见证向量长度。
$$
\vec{w} = \begin{bmatrix} w_0 & w_1 & \cdots & w_n \end{bmatrix} $$
$$
A =
\begin{bmatrix}
a{00} & a{01} & \cdots & a{0n} \
a{10} & a{11} & \cdots & a{1n} \
\vdots & \vdots & \ddots & \vdots \
a{m0} & a{m1} & \cdots & a_{mn}
\end{bmatrix}
$$
$$
B =
\begin{bmatrix}
b{00} & b{01} & \cdots & b{0n} \
b{10} & b{11} & \cdots & b{1n} \
\vdots & \vdots & \ddots & \vdots \
b{m0} & b{m1} & \cdots & b_{mn}
\end{bmatrix}
$$
$$
C =
\begin{bmatrix}
c{00} & c{01} & \cdots & c{0n} \
c{10} & c{11} & \cdots & c{1n} \
\vdots & \vdots & \ddots & \vdots \
c{m0} & c{m1} & \cdots & c_{mn}
\end{bmatrix}
$$
最后,通过每个矩阵对见证向量进行线性变换,使得约束系统可以通过向量等式检查得到完全表示。
$$ A \vec{w} ∘B \vec{w} =C \vec{w} $$
虽然 Groth16 SNARK 在从 R1CS 变为完全成熟的 SNARK 时需要额外的变换,即将向量转换为多项式以适应多项式承诺方案,但这超出了本文的范围,因为重点在于开发者需要了解的实际目标。
示例
对于具体示例,我们将以下程序转换为 R1CS。
$$ z=x^2∗y $$
fn main(
x: pub Field,
y: pub Field
) -> pub Field {
let z = Field::pow_32(x, 2) * y;
z
}注意:
**操作符不是有效的 Noir 语法,因此我们在Field命名空间中使用pow_32内置函数。
首先我们将表达式简化为简单的乘法等式检查。
fn mul_only_main(
x: pub Field,
y: pub Field
) -> pub Field {
let x_sq = x * x;
let z = x_sq * y;
z
}接下来我们推导出我们的见证向量,其中必须包含所有输入,输出,中间值和 1。
w→=[1xyxsqz]
$$
\vec{w} = \begin{bmatrix} 1 & x & y & x_{sq} & z \end{bmatrix} $$
然后我们推导出 'A'、'B' 和 'C' 矩阵。将上述函数 mul_only_main 视为一系列 'a*b=c' 约束,我们得到如下。
$$ x \cdot x = x_{sq} \
x_{sq} \cdot y = z
$$

我们将 'A' 定义为:
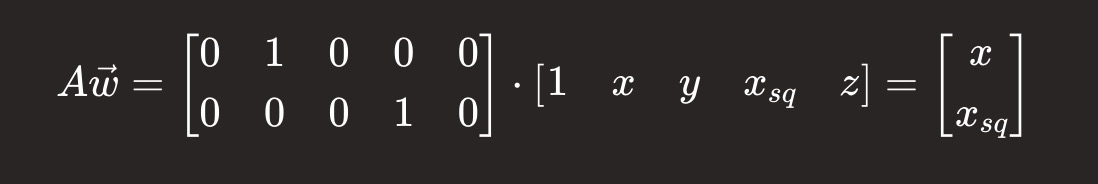
分别定义 'B' 和 'C':
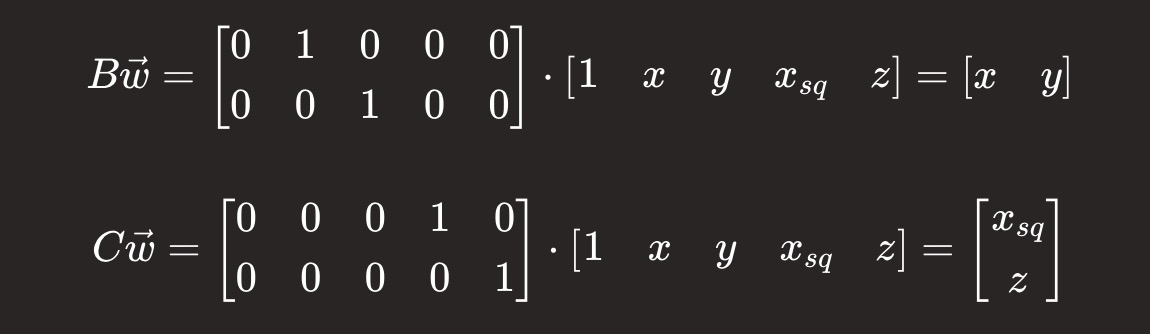 最后,我们可以约束条件为:
最后,我们可以约束条件为:
$$ A \vec{w} ∘B \vec{w} =C \vec{w} $$
关于 'A'、'B' 和 'C' 矩阵,一个有用的思路是将其视为选择器,定义了给定行上受约束的见证向量元素。
PLONK 类约束系统
PLONK 类约束系统同样要求电路是一系列约束,尽管每个约束中有更多的元素。
注意:我们称之为 PLONK 类,因为 PLONK 的变体使用相同的基础约束系统但具有各种扩展。
$$ q_L⋅a+q_R⋅b+q_O⋅c+q_M⋅ab+q_C=0 $$
我们视 'q' 值为选择向量,'a'、'b' 和 'c' 值为赋值向量。通过使用不同组合的选择器,我们可以在不修改约束系统的情况下约束几种不同的属性。
乘法(a * b = c):
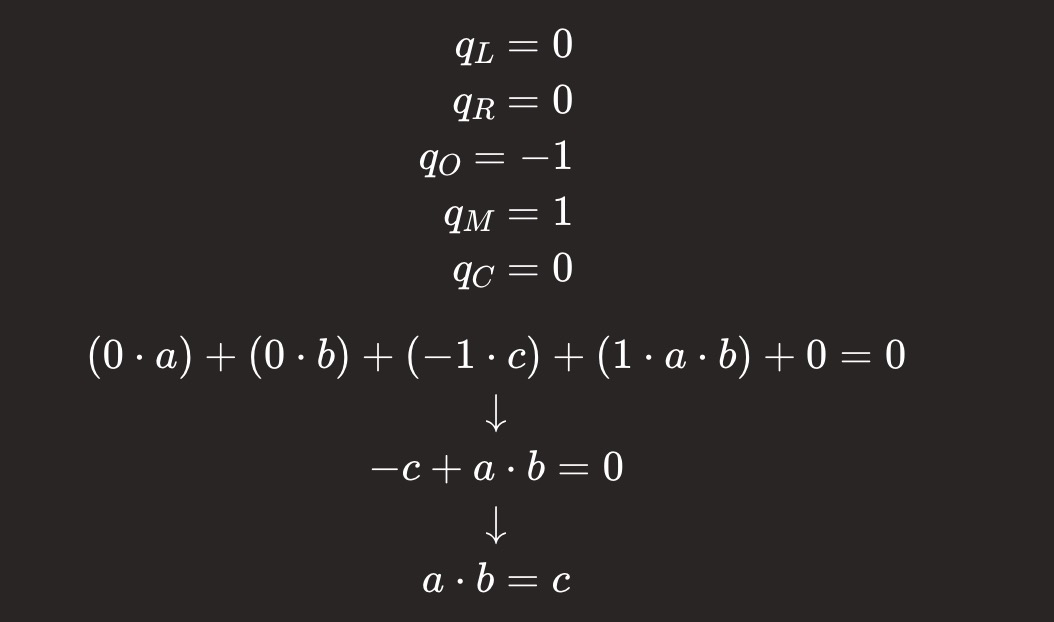
加法(a + b = c):
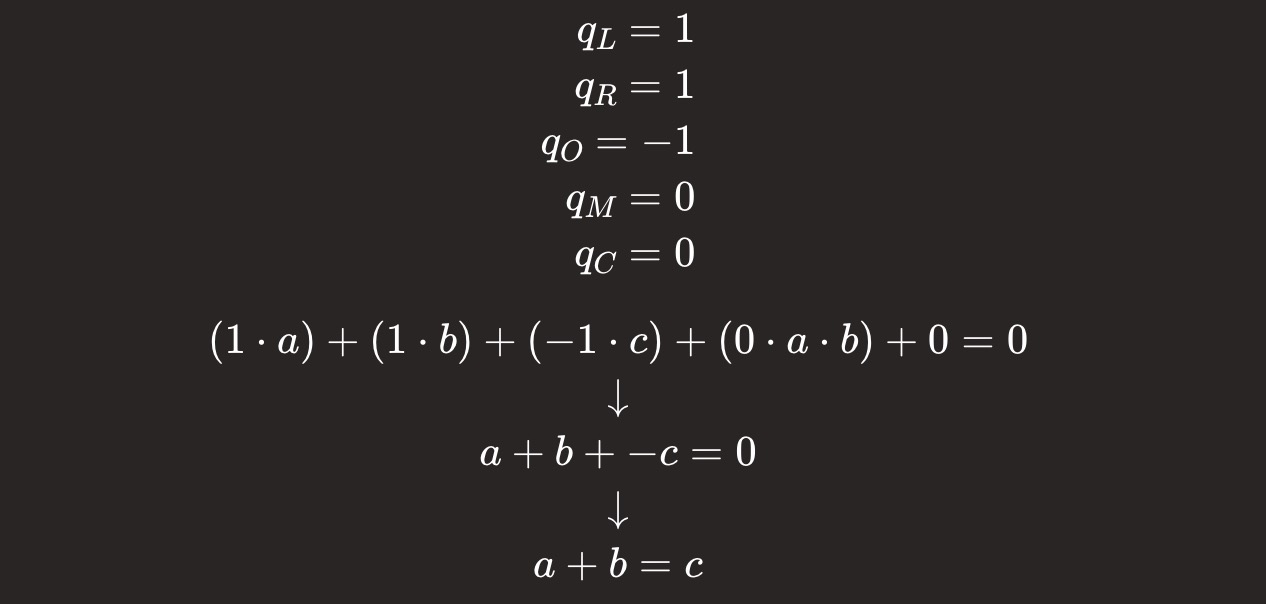
布尔性(a = 0 || a = 1):
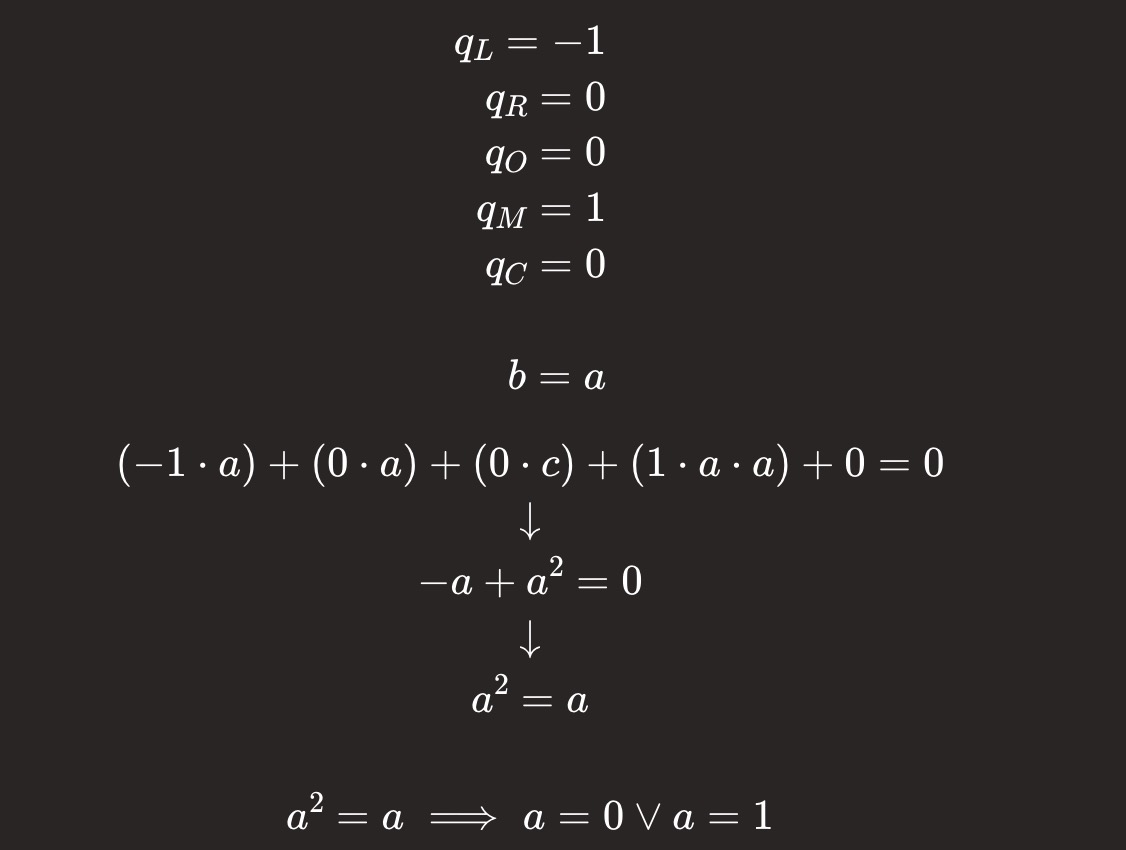
常量(a = 5):
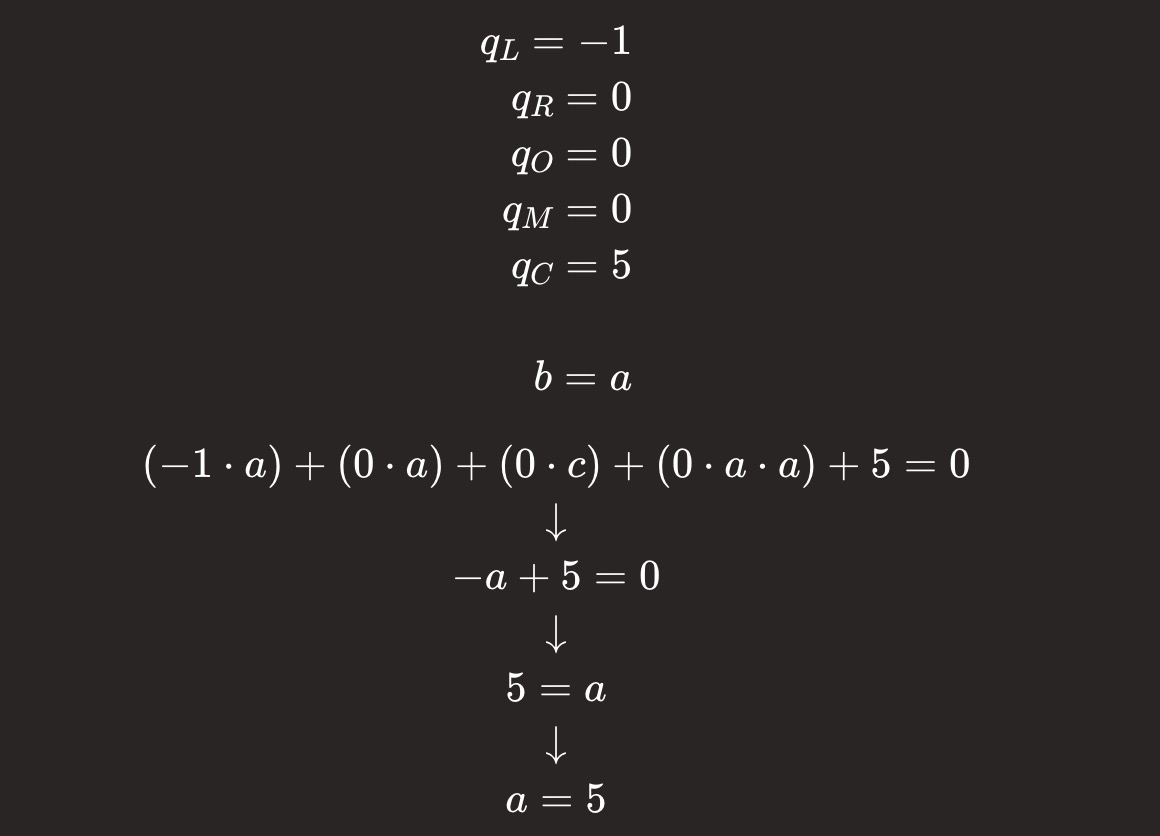
同样,我们定义赋值向量 'a'、'b' 和 'c' 以及选择器向量 'qL'、'qR'、'qO'、'qM' 和 'qC',使得以下条件成立。
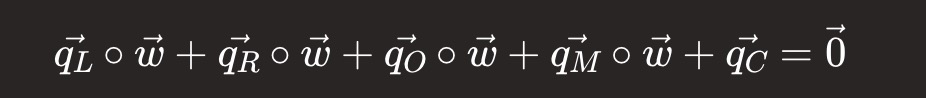
示例
作为具体示例,我们将以下程序转化为 PLONK 约束系统。
$$ z=x^2∗y+5 $$
首先,我们将表达式拆分为可以通过 PLONK 的某一行证明的行。
fn main(
x: pub Field,
y: pub Field
) -> pub Field {
let z = Field::pow_32(x, 2) * y + 5;
z
}
fn plonk_main(
x: pub Field,
y: pub Field
) -> pub Field {
let x_sq = x * x;
let z = x_sq * y + 5;
z
}注意:
**操作符不是有效的 Noir 语法,因此我们在Field命名空间中使用pow_32内置函数。
将上述函数 plonk_main 视作为一系列 PLONK 约束,我们将每个表达式转换为 PLONK 类约束。
let x_sq = x * x;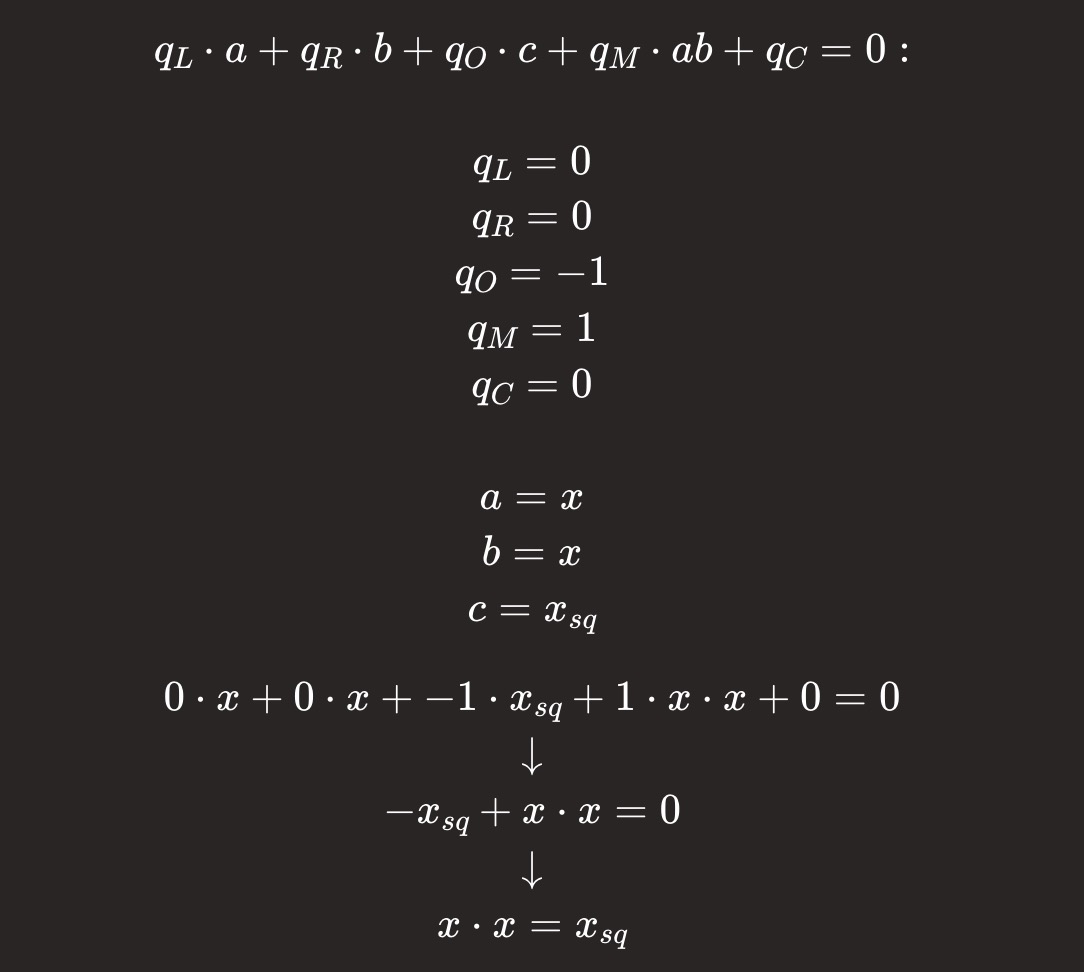
let z = x_sq * y + 5;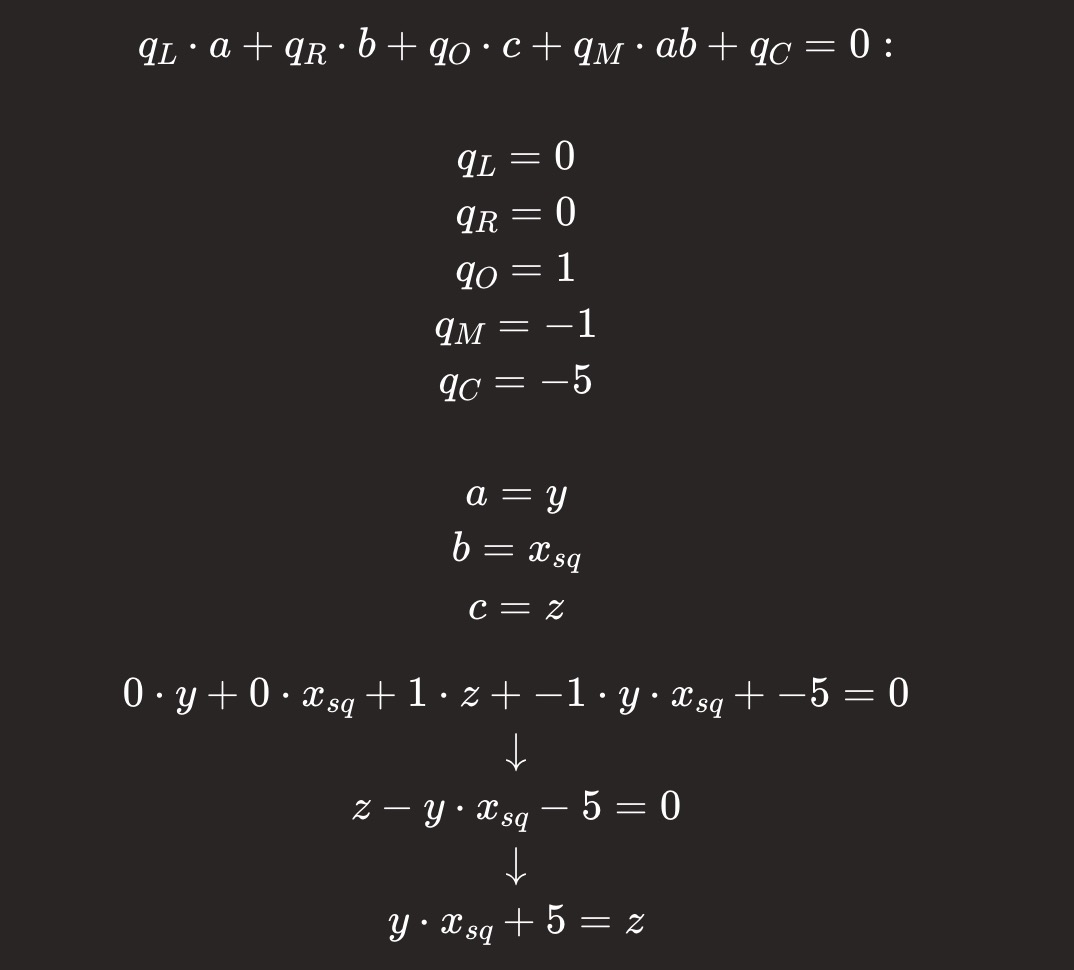
然后将它们组合成向量:
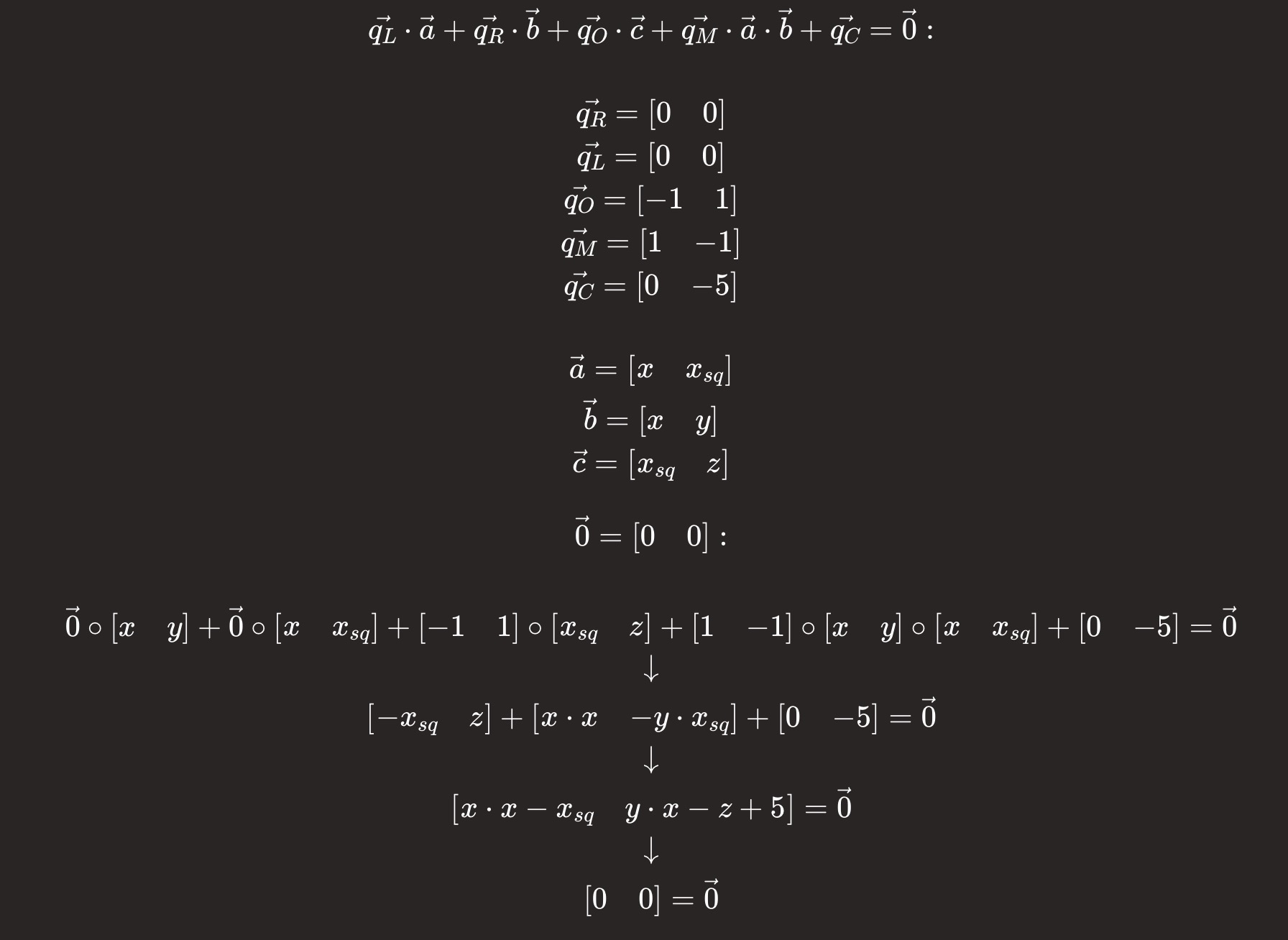
然而,左侧只有在所有约束被满足时才减少到零向量。
Noir 输出
鉴于 PLONK 约束示例,我们将审查以下 Noir 程序的编译阶段,以确保其与我们在示例部分展示的相匹配。
fn main(
x: pub Field,
y: pub Field
) -> pub Field {
let z = Field::pow_32(x, 2) * y + 5;
z
}我们将使用打印 ACIR 的选项编译代码。
nargo compile --print-acir这打印出以下内容。
编译的 ACIR 适用于 main(未优化):
func 0
当前见证索引:3
私有参数索引:[ ]
公共参数索引:[0, 1]
返回值索引:[2]
EXPR [ (1, _0, _0) (-1, _3) 0 ]
EXPR [ (-1, _1, _3) (1, _2) -5 ]主函数的 ID 为 0。
3 的当前见证索引表示见证中有四个值(在被 ACVM 解释时将转化为 ‘a’、‘b’ 和 ‘c’ 赋值向量)。
没有私有参数,但有两个公共参数,其见证索引分别为 0 和 1;这对应于我们的输入 x 和 y。
有一个返回值索引,2,对应于 z。
尽管我们没有明示确认 x_sq 在元数据中的存在,但可以推断出见证向量是:
w→=[xyzxsq]
$$
\vec{w} = \begin{bmatrix} x & y & z & x_{sq} \end{bmatrix} $$
接着我们有两个 EXPR 表达式。检查 ACIR 存储库 中的 ACIR 操作码,我们发现唯一一处 Expression 出现在 Opcode::AssertZero(Expression) 中,它似乎在它自己的模块中定义。
pub struct Expression<F> {
pub mul_terms: Vec<(F, Witness, Witness)>,
pub linear_combinations: Vec<(F, Witness)>,
pub q_c: F,
}mul_terms 字段包含一系列三元组,每个三元组包含一个选择器和两个见证值('a' 和 'b'),而 linear_combinations 字段包含一系列元组,每个元组包含一个选择器和一个见证值('c'),最后 q_c 字段包含常量值('qC')。
利用这些信息,我们可以重建表达式如下。
let witness = [x, y, z, x_sq];
// 0*x + 0*x + 1*x*x - x_sq + 0 = 0
//
let expr_0 = Expression {
mul_terms: vec![(1, witness[0], witness[0]),],
linear_combinations: vec![(-1, witness[3])],
q_c: 0
};
// 0*x + 0*x - 1*y*x_sq + 1*z + 5 = 0
//
let expr_1 = Expression {
mul_terms: vec![(-1, witness[1], witness[3])],
linear_combinations: vec![(1, witness[2])],
q_c: -5
};这与我们的 PLONK 约束是一致的!
结论
为了简洁起见,自定义门和查找表将在此暂时留白。然而,作为 Noir 电路后端的 PLONK 类约束系统的基础应该有助于建立对编译器行为的直观认识,以及如何通过将耗时的计算任务委派给 Brillig 不受约束环境来优化电路。
期待未来有更多类似内容,因为还有许多内容未涵盖。
- 原文链接: jtriley.substack.com/p/n...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 在浏览器中生成零知识证明, 今天就可以 643 浏览
- 在 ZK 电路中发现健全性错误的实用指南 957 浏览
- ZK编年史:电路(第一部分) 965 浏览
- Circom 常见陷阱及规避方法 — 第二部分 675 浏览
- Privacy Pool 隐私池的设计 2587 浏览
- GKR 教程 - 加速零知识证明的密码学方案 - Vitalik 1355 浏览
- zkVM、电路与优化博弈 2121 浏览
- Passkey ECDSA 验证的 ZKP 系统基准测试 1560 浏览
- UltraGroth 原理分析 909 浏览
- ZK 月报:2025年8月回顾 1681 浏览
- 旋风路:使用WHIR作为多项式承诺方案的多线性STARKs 484 浏览
- 构建安全Noir电路的开发者指南 293 浏览

