Stwo 中的递归证明：第二部分

在 第一部分 的文章中，我们提供了递归证明的背景，以及它们在 Stwo 中扩展到无界计算的重要性。我们与 StarkWare 合作构建了 Stwo 的递归系统，该系统由两个组件组成：Plonk 和 Poseidon。

我们已经介绍了 Plonk 组件的细节，以及它如何用于表示不同类型的算术关系，因此可以用于验证各种计算。在本文中，我们将重点关注另一个组件 Poseidon，它确实具有更棘手和更复杂的设计。

Stwo 的完整递归证明生成已经完成，可以在 GitHub 中找到相关的源代码：

• 证明系统: https://github.com/Bitcoin-Wildlife-Sanctuary/stwo-circle-poseidon-plonk

• 递归电路: https://github.com/Bitcoin-Wildlife-Sanctuary/recursive-stwo

• 比特币验证器: https://github.com/Bitcoin-Wildlife-Sanctuary/recursive-stwo-bitcoin

现在让我们深入了解证明系统的 Poseidon 组件的细节。

哈希函数在 STARK 中的作用

我们刚刚提到，已经在第一部分文章中讨论过的 Plonk 组件可以表示各种计算，这当然也包括 Poseidon 哈希函数。有人可能好奇为什么我们需要证明系统中一个专门的 Poseidon 组件，因为可以直接使用 Plonk 来处理相同的计算。

原因是 Plonk 中验证 Poseidon 的成本。在作为递归一部分的整个 STARK 证明验证过程中，有几个地方涉及哈希函数，如下图所示。

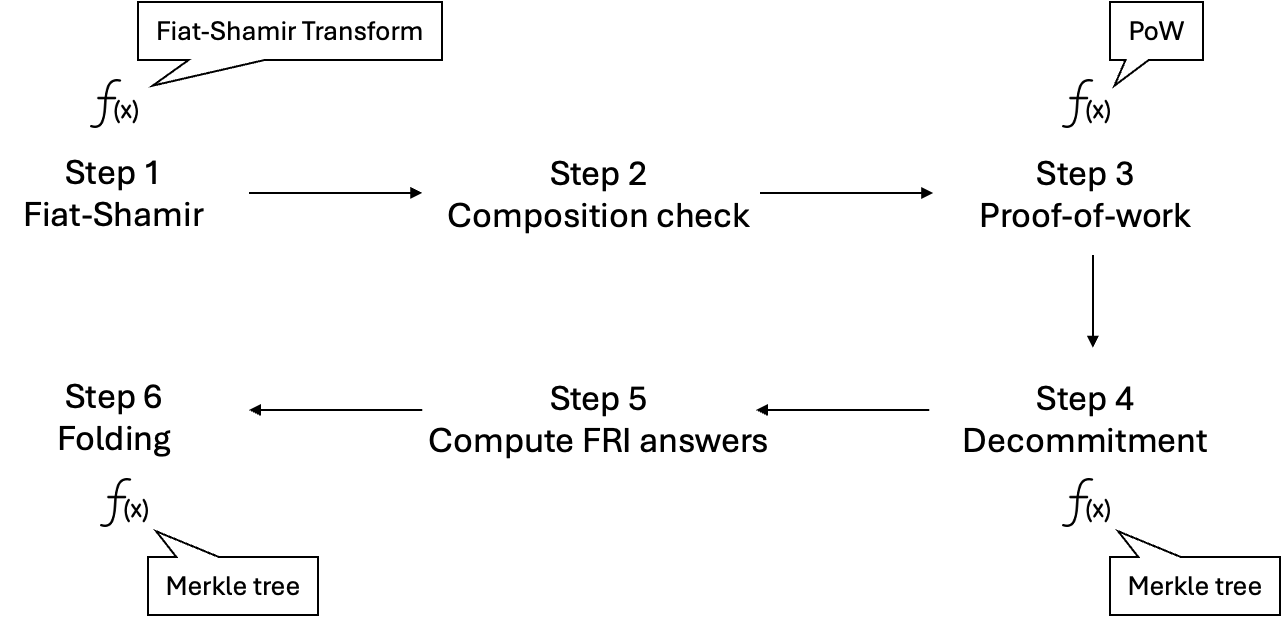
STARK 使用 Fiat-Shamir 变换，用于在零知识证明中生成随机性。此变换使用哈希函数的输出来获得这种随机性。Fiat-Shamir 变换的具体过程与证明系统和电路的“大小”有关。当正在递归验证的证明系统有很多列时，Fiat-Shamir 变换最终可能会多次调用哈希函数。

然后，STARK 还使用工作量证明（也称为 grinding）作为验证者的优化。这也将要求验证者计算哈希函数，但通常只有一次。

Fiat-Shamir 变换和工作量证明之后的所有内容都与 Merkle 树 有关——在 STARK 证明生成期间，一些数据被提交到 Merkle 树中，并且验证者在随机位置打开 Merkle 树以检查数据是否匹配。这将构成涉及哈希函数的大部分开销，因为 STARK 证明验证需要打开多个 Merkle 树，并且由于需要在许多随机位置进行检查，因此该过程会重复几次。

实验表明，在进行递归证明验证时，涉及哈希函数的开销很容易成为主要的开销。这需要加以处理，因为我们最终希望在比特币或以太坊上验证 Stwo 证明，这要求我们能够将更大的证明递归成一个小的证明。如果递归电路过于复杂，可能会遇到递归最终会增加验证开销的问题，因为递归电路比我们关心的应用要大。

既然我们已经讨论了为什么 Poseidon 需要更多的专门工作，而不是直接使用 Plonk 来计算 Poseidon 哈希函数，我们想谈谈它的开销，以及专门的列如何帮助更快地验证 Poseidon 哈希函数。

Poseidon 哈希函数

我们使用的哈希函数是 Poseidon2。今天，这是一个经过充分验证的哈希函数，几乎成为了王储，特别是因为许多其他 ZK 友好的哈希函数，包括 Griffin、Arion、Anemoi、Rescue，都已被证明比最初预期的 更弱，并且需要更大的参数（参见 [1], [2], [3]）。

我们在 Mersenne-31 域上实例化 Poseidon2 哈希函数。每个输入或输出都包含以下 sponge 结构 的两个部分：一个称为 rate，预计是公开的，另一个称为 capacity，预计保持私有。

为了实现 128 位的安全性，每个 rate 和 capacity 都需要至少（大约）256 位，因此我们将 rate 和 capacity 设置为各自包含 8 个 M31 元素。也就是说，哈希函数的输入或输出将有 16 个 M31 元素，如下所示。

Poseidon2 将对输入执行一系列转换以生成输出。在较高的层面上，它从一些线性变换开始预处理输入，然后继续进行 4 轮完整轮、14 轮部分轮，然后进行 4 轮完整轮。

请注意，完整轮是这种变换的前 4 轮和后 4 轮。这就是它也获得“外部”轮的名称的原因，因为它们封装了中间的 14 轮部分轮，因此也被称为“内部”轮。

完整轮与部分轮的不同之处在于，完整轮执行更繁重的计算，而部分轮更轻量级——尽管如此，部分轮的数量更多。由于我们需要详细了解我们的 Poseidon 组件，因此现在应该讨论完整轮和部分轮的工作方式。

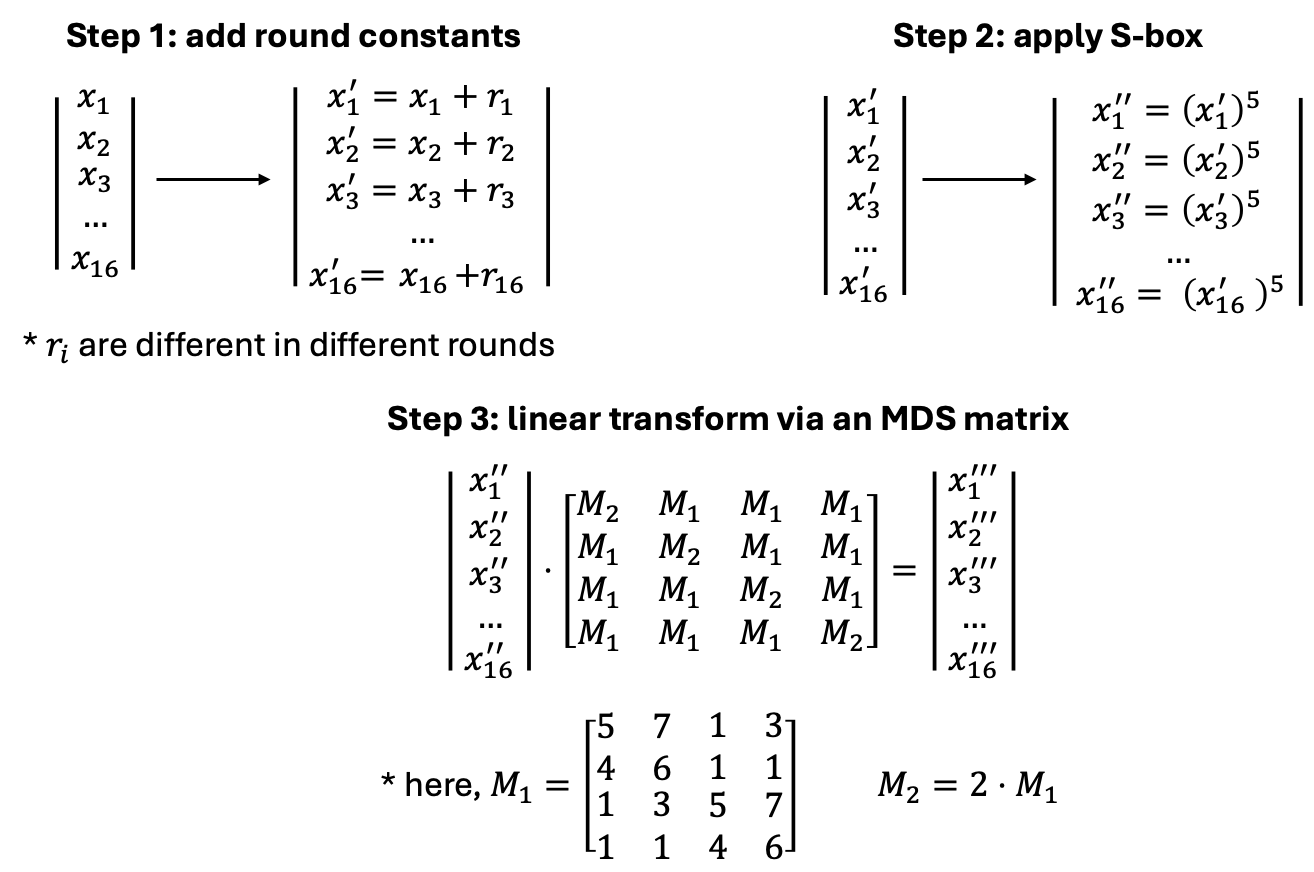
完整轮。 在 Poseidon2 中，完整轮执行三个步骤。

• 将当前状态（rate 和 capacity，总共 16 个元素）与轮常量相加，轮常量是特定于轮的、固定但随机的 M31 元素。

• 将 S 盒应用于状态的每个元素。在我们的例子中，S 盒将 x 映射到 x^5。

• 使用 16x16 MDS 矩阵执行线性变换。

第一步和最后一步是线性变换（已知和固定常数的加法和乘法），在 ZK 电路中表示它们非常简单。第二步涉及 5 次算术变换。

以前，如果我们使用 Plonk 来表示这种关系，我们会遇到这样的问题：Plonk 组件中的每一行只能执行一次加法或一次乘法，因此，完整轮会生成多行。

• 第一步，添加轮常量，基本上会生成 16 行，而每一行都会将状态中的一个元素加上一个相应的常量。

• 第二步，应用 S 盒，将贡献 48 行，而每三行负责将一个元素从 x 映射到 x^5。

• 最后一步，执行 MDS 矩阵，可能是最昂贵的，因为它会贡献 120 行。

这加起来每轮完整轮需要 184 行。我们将在本文后面展示如何在 Poseidon 组件的一行中完成 2 轮的完整轮。

部分轮。 完整轮中的计算被称为“完整”，因为状态中的每个元素（总共 16 个元素）都获得了 S 盒。由于 S 盒比其余操作消耗更多的计算资源，因为它涉及乘法，而其余操作可以通过加法来实现，因此研究人员决定在保持安全性的前提下减少 S 盒的使用，但代价是需要更多的轮（更频繁的“扩散”）。

因此，在 Poseidon2 中，除了开头和结尾的 4 轮完整轮之外，还有 14 轮部分轮位于它们之间（因此称为内部轮）。它也有三个步骤，但每个步骤的计算要轻得多：

• 将*第一个元素*与轮常量相加，而其余 15 个元素保持不变。

• 仅将 S 盒应用于*第一个元素*，同时保持其余元素不变。

• 执行轻量级矩阵的线性变换。

在 Plonk 中实现部分轮是可能的，成本会低于完整轮，但仍然很高。

• 第一步仅生成一行。

• 第二步仅生成三行。

• 最后一步涉及 47 行。

这加起来每轮部分轮需要 51 行，并且有 14 轮这样的轮。但是，我们可以做得更好。我们稍后将展示如何在 Stwo 中使用 Poseidon 组件在一行中完成 14 轮部分轮。

优化思路

在我们介绍 Poseidon 模块的构造之前，我们首先要讨论如何从基线（使用 Poseidon）进行优化，以及为什么这种优化是可能的。

请记住，在第一部分文章中，prover的开销是由列数乘以行数（换句话说，证明系统中单元格的数量）决定的。

当我们使用 Plonk 证明系统来表示计算时，请记住每一行都可以执行一次加法或一次乘法，并且每一行都有 10 + 12 + 8 = 30 列。根据我们上面的计算，整个 Poseidon 评估需要 2186 行，相应地需要 65580 个单元格。

这与我们稍后将展示的构造形成对比，后者在 Poseidon 组件中使用 6 行，其中 Poseidon 组件有 96 列。这仅使用 576 个单元格，使 prover 时间至少提高了 114 倍。

导致基线方法速度变慢的原因有很多，但我们可以将其概括为两个方面：

• 当运行 Poseidon 函数时，Plonk 证明系统有太多未得到充分利用的列。

• Plonk 证明系统无法有效地表示 Poseidon 函数中的线性运算。

未得到充分利用。 请记住，我们讨论的 Plonk 证明系统使用 QM31 作为元素。但是，我们使用的 Poseidon2 哈希函数是在 M31 上定义的。这已经意味着在 12 个“trace”列中，有 9 个是虚拟的，并且都为零。

然后，请记住，Plonk 证明系统的其余部分负责将变量从一行传递到另一行。实际上，许多列都用于此目的。例如，在 10 个预处理列中，“a_wire”、“b_wire”、“c_wire”这三列用于为 A、B、C 变量提供标识符，而“mult_a”、“mult_b”、“mult_c”这三列用于 logUp 参数。对于每一行，我们还有 8 个用于 logUp 的交互列。

这意味着，当我们对 16 个元素执行加法时，我们需要 16 行，并且每一行都需要独立和专用的 logUp 列。但是，实际上，这些 16 个元素通常是分批处理的，并且作为哈希函数计算的中间变量，它们不会在证明系统的其他地方使用，而只是立即被后续轮（Poseidon 函数中的 4+14+4 轮）消耗。使用 logUp 参数将变量传递到证明系统中任何其他行（任意次数）的能力是过度的。

可以将 Plonk 证明系统视为非常通用的 CPU，它具有随机访问存储器——数据可以被读取或写入任意次数，在程序的任何位置——并且还具有高的 CPU 字长，可以同时处理 4 个元素，但我们在评估 Poseidon 哈希函数时通常只使用一个元素。此 CPU 不了解我们正在执行的批处理操作，并且它获取和放置批处理中的每个元素，并将它们视为无关的。

我们通过将 Poseidon 证明系统设计为专用 CPU 来解决这种未充分利用的问题，该 CPU 可以批量执行操作，包括批量访问内存，并且还通过在每次访问之间执行更多计算步骤来减少对内存的访问。它每行处理 16 个元素。在它使用 logUp 参数之前，它要么在该行中应用 2 轮完整轮，要么在该行中应用 14 轮部分轮，而以前甚至一轮可能需要 51 到 184 行。

我们很快将介绍详细信息，但是可以看出，消除 Plonk 证明系统的冗余和未充分利用可以大大降低 prover 的成本。

效率低下。 速度变慢的另一个原因是它没有以最有效的方式表示线性关系。例如，考虑一轮完整轮。如果我们使用 Plonk 证明系统来实现完整轮，则完整轮的所有三个步骤——添加轮常量、应用 S 盒和执行线性变换——都会导致行数增加，并且我们知道线性变换贡献最大。这些行会导致单元格增加，从而导致 prover 效率低下。根据我们之前的计算，一轮完整轮会导致 5580 个单元格。

但是，如果我们只关注与完整轮相关的计算，以最纯粹的形式，这似乎可以用 48 个单元格来完成：16 个单元格用于轮常量，16 个单元格用于输入，16 个单元格用于输出。请注意，轮常量是 prover 不需要每次都提交的预处理列。

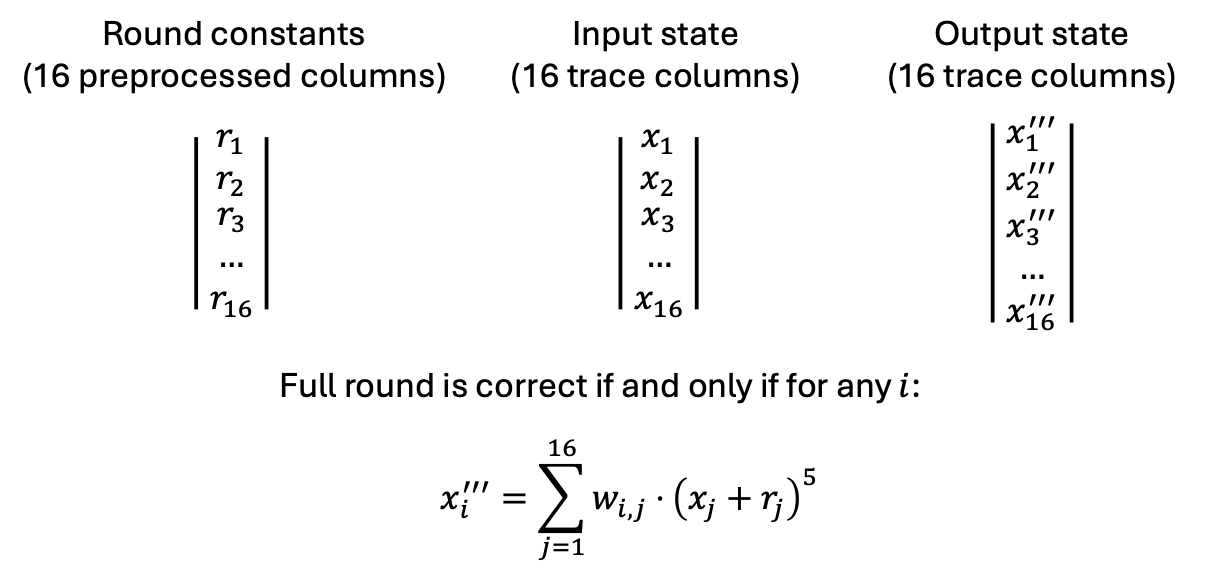
当然，这些列之间的等式更复杂——它是 5 次的，涉及很多变量，但它的确很容易验证。

• 加法计算起来非常高效。

• 所有权重（图中的 w_{i,j}）都是非常小的值，并且有算法可以非常有效地评估它（MDS 矩阵）。

通过使用这些等式来整体处理 16 个元素，计算中涉及的单元格数量显着减少——在上面的示例中，你可以看到添加轮常量不会引入额外的列（除了 prover 不需要计算的轮常量预处理列），并且通过 MDS 矩阵的线性变换也不会导致列增加。

这也适用于部分轮。应用相同的经验法则，我们知道对于每个部分轮，添加轮常量（仅涉及*第一个元素*）仅需要一个预处理列，但没有其他列，并且线性变换将不涉及任何列。这样，处理 14 轮只需要大约 14 + 16 + 16 = 46 列。

由于 46 小于 48，因此我们实际上可以让完整轮和部分轮共享列。有些行用于“完整轮”，因此这些列用于完整轮计算，而另一些行用于“部分轮”，其中相同的列反而用于部分轮计算。

我们的构造

我们在这里介绍 Poseidon 组件的总体构造，但我们跳过了有关 logUp 参数的详细信息，这我们在第一部分文章中已经讨论过了。我们将介绍一个简化的版本，想要了解完整版本的读者可以查看我们在 GitHub 上的实现 这里。

每次调用 Poseidon 哈希函数都会在 Poseidon 组件中创建 6 行。有两个控制列：“First round?” 和 “Full round?”，它们在这 6 行中发生变化，并且它们直接影响输入、中间、输出的 48 列的使用方式。

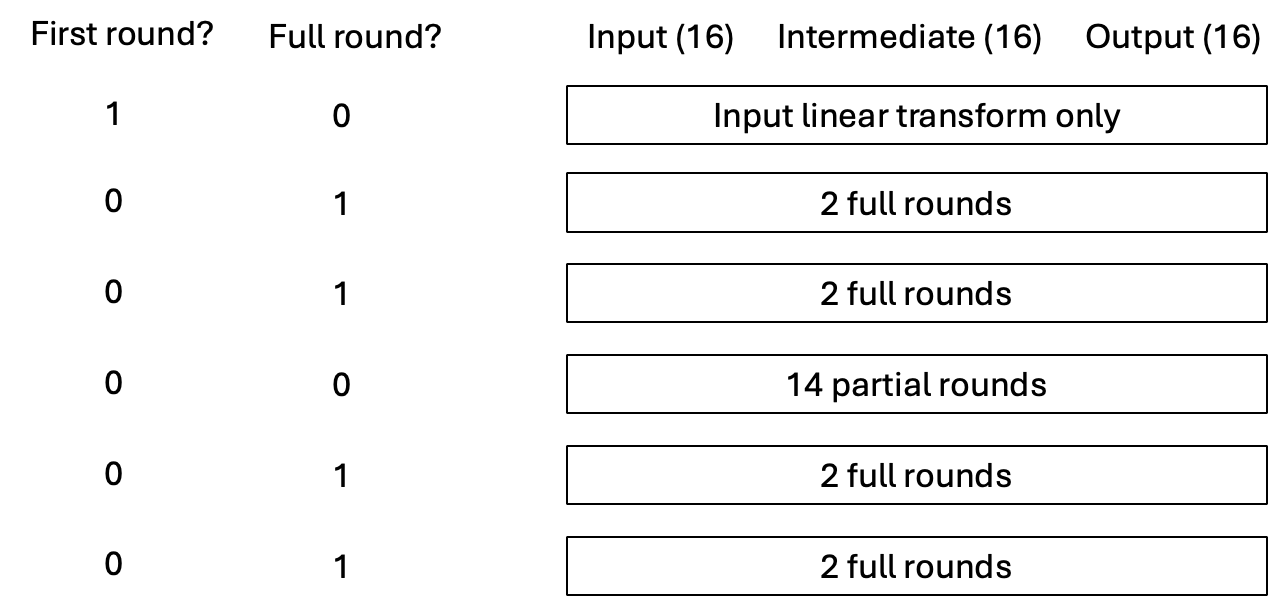
第一行对输入执行线性变换（MDS 矩阵），跳过 S-Box 或轮常量。这是 Poseidon2 中一个标准且必要的预处理步骤。近年来，这样做对于安全性而言非常重要。

在第一行之后，我们有第二行和第三行用于前 4 轮完整轮，其中每一行负责处理总共两轮完整轮。每行中，

• 第一轮完整轮应用于 16 个输入列，并将其输出写入 16 个中间列。

• 第二轮完整轮应用于 16 个中间列，并将其输出写入 16 个输出列。

我们在这里跳过的 logUp 参数负责将第一行的输出（线性变换后的输入）连接到第二行的输入，依此类推。

第四行，其 “First Row?” 和 “Full round?” 都设置为零，将完成所有 14 轮部分轮。我们将前 4 轮完整轮后的结果存储在输入中，并将 14 轮部分轮后的结果存储在输出中。至于中间列，由于这样做的一些技术必要性，我们使用其中的 14 个（总共 16 个）来存储每轮中 S-box 之后的第一个元素。

然后，我们继续进行另外两行，每一行负责 2 轮完整轮。这样，我们就完成了 Poseidon 哈希函数的 4 + 14 + 4 轮的所有轮。

在我们的实现中，Poseidon 组件中还有一些其他的列和逻辑，我们在这里没有介绍：它们负责行之间以及与 Plonk 组件之间的输入和输出（通过在 Part1 文章中讨论的 logUp 参数）。我们还让 Poseidon 组件负责在给定一位的情况下交换输入的前半部分和后半部分，这主要用于 Merkle 树路径验证。这种扩展的详细信息可以在代码中找到，但每次 Poseidon 评估仍然只贡献 6 行。

编写递归电路

用于 Stwo 中递归证明验证的完整证明系统是 Plonk 组件和 Poseidon 组件的组合。我们主要在 Plonk 组件中进行编程，只有当我们使用 Poseidon 哈希函数时，才会在两个组件中进行编程。

我们使用类似于我们用来编写比特币脚本的 DSL（我们在 之前的一篇文章 中讨论过）在 Rust 中编写递归电路。此 DSL 允许我们将 StarkWare 的 Stwo 库中的现有 Rust 代码转换为电路的 DSL 代码。

例如，在 Poseidon 组件中，我们需要在一轮完整轮中执行线性变换，StarkWare 的 Stwo 库中的相应 Rust 代码（这里）如下所示。这段 Rust 代码接收四个字段元素（x[0]、x[1]、x[2]、x[3]），执行一系列加法，并将一些值作为结果输出（t6、t5、t7、t4）。

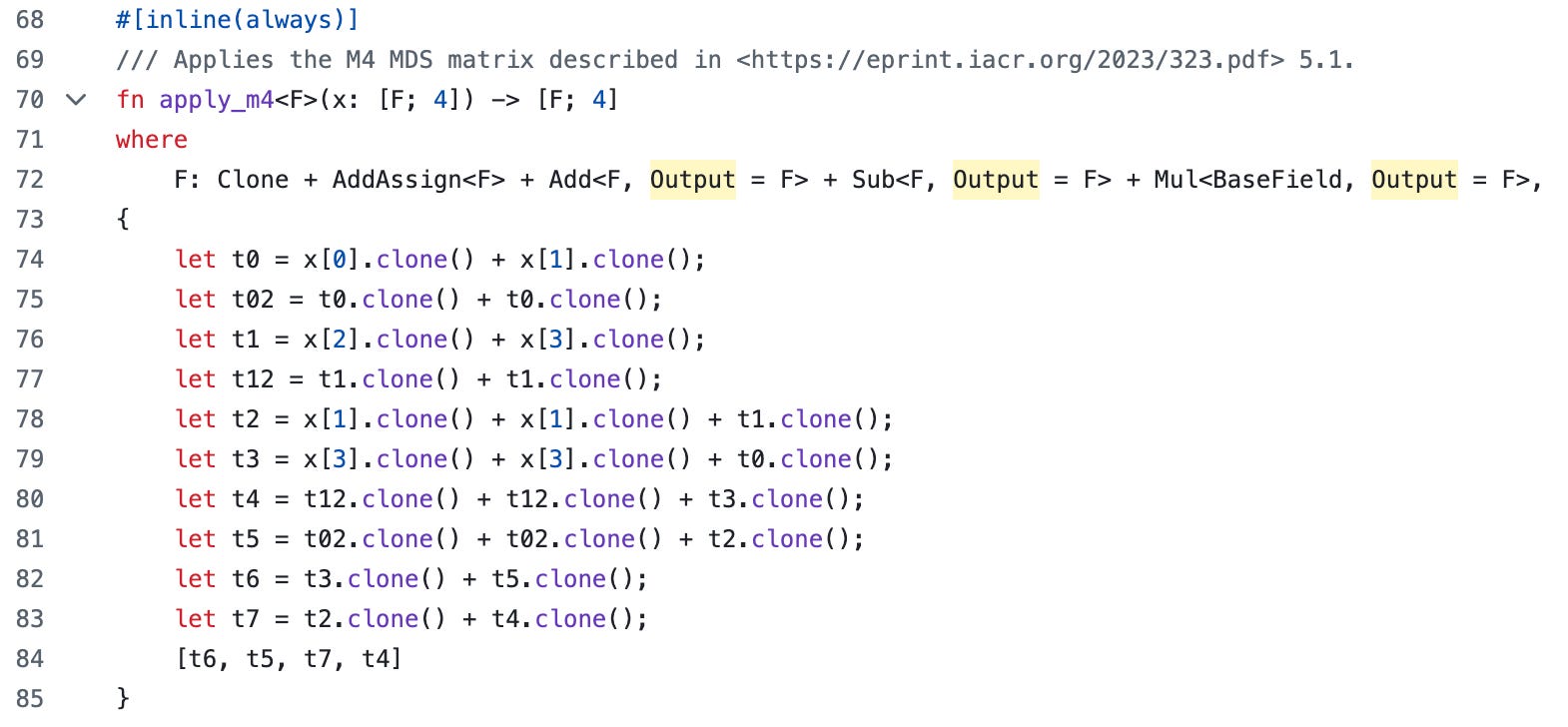
当我们编写递归电路时，我们基本上采用相同的代码，只进行一些机械编辑，如下所示。机械编辑包括对变量使用“QM31Var”，这是一种由 DSL 驱动的数据结构，能够记录 DSL 的操作，并将“clone”更改为按引用传递。

此 DSL 还允许我们将 StarkWare Stwo 库中的现有数据结构和数组镜像到由 DSL 驱动的数据结构和数组中。

例如，在 Stwo 中，我们有一个 “ColumnSampleBatch”，用于将评估点和列排列在一起。我们可以在 DSL 中创建一个一一对应的映射，称为“ColumnSampleBatchVar”，并且当我们直接从 Stwo 调整代码时，我们可以使用它来代替 “ColumnSampleBatch”。

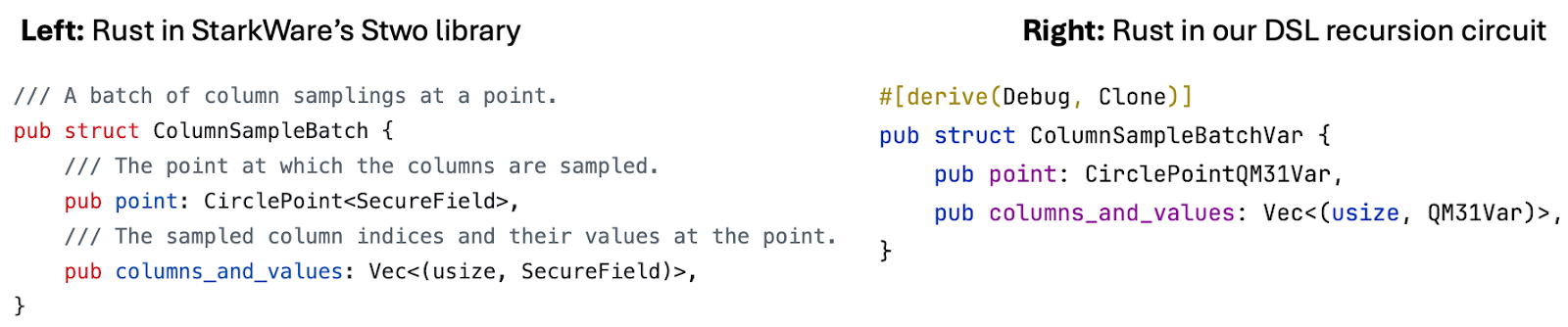
我们按照此过程在 DSL 中实现整个 STARK 验证器。在我配备 M3 Max 芯片（由 Starknet 空投资助）和 14 个内核的 2023 MacBook Pro 上，递归一个适度大小的证明大约需要 1 秒到 3 秒。

为了给出一个具体的数字，我们使用以下配置运行了一个基准测试。

• 递归电路验证一个证明，该证明也是一个递归电路，Plonk 组件中有 2^16 行，Poseidon 组件中有 2^16 行。

• 被验证的证明针对 prover 效率进行了优化，并牺牲了 verifier 效率（这是使用递归的典型示例），方法是使用 2 的 blow-up 系数。

• 上述验证总共重复 5 次。

以下是 Stwo STARK 证明验证的每个步骤在一次验证（五次重复中的一次）中行数的分解。

• Fiat-Shamir: Plonk 组件中有 1189 行，Poseidon 组件中有 840 行。

• Composition: Plonk 组件中有 2063 行，没有 Poseidon 行。

• 计算 FRI 答案和去承诺: Plonk 组件中有 176947 行，Poseidon 组件中有 42720 行。

• Folding: Plonk 组件中有 51682 行，Poseidon 组件中有 120480 行。

在我的笔记本电脑上生成这样的证明需要 14.27 秒。平均而言，每次递归验证一个证明需要 2.85 秒。

请注意，如果证明适用于更大的电路，或者如果证明使用更高的 blowup 系数（这将显着降低验证开销），则递归时间将有所不同。具体来说，如果我们把 blowup 系数从 2 增加到 4，计算 FRI 答案和 folding 的工作量将减半。

我们预计使用具有更多内核的机器将进一步提高延迟——但这可能不应该是优化的重点。正如我们在第一部分文章中提到的，递归的力量在于允许将非常大的计算任务（例如，验证以太坊中的一个区块）切片成许多小块，并分配给大量的实例，其中每个实例负责一个或几个块。

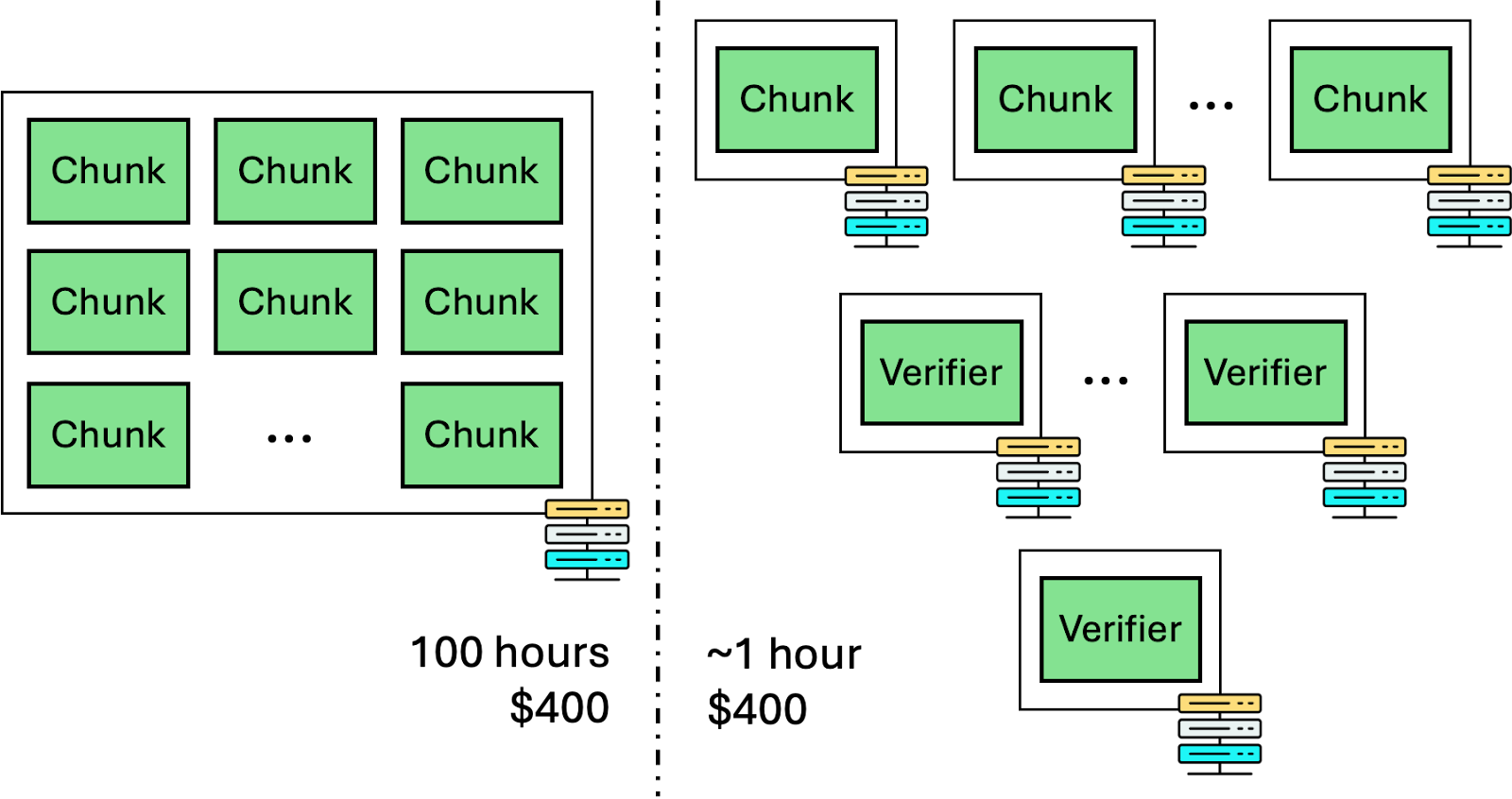
然后，当实例完成每个块的证明生成时，它们使用递归将证明合并在一起。

让我们做一个具体的计算。假设原始计算需要大约 100 个小时才能完成。将其切片成 100 个块，我们可以让 100 台机器在一小时内完成相应的块。

然后，我们使用 20 台机器，每台机器通过上述递归电路将 5 个证明合并成一个证明，这可能需要 15 秒，并产生 20 个证明。然后，我们使用 4 台机器并重复相同的过程，这又需要 15 秒，并且只会产生 4 个证明。我们只需要使用一台最终的机器来合并证明，这大约需要 12 秒。这只会给原始计算增加不到 1 分钟的额外开销。

正如第一部分文章所说，这从根本上改变了我们扩展 ZK 证明的方式。以前，我们可能会尝试通过使用具有数百个内核的强大机器来优化单台机器的 prover 效率。在实践中，已经表明使用多个内核不会线性地提高性能——你可能已经将内核数量从 16 个增加到 192 个，但性能提升小于 2 倍。

这在实践中非常常见，并且通常限制了 ZK 的单个证明生成的可扩展性。递归一直是打破这种限制的唯一方法。与使用更大的机器相比，让多台较小的机器更加高效和经济。

在比特币 STARK 验证器中的使用

我们构建的递归验证器也用于比特币 STARK 验证，它将更适合 prover 的 ZK 证明转换为更适合 verifier 的 ZK 证明。通过多次重复此步骤，我们可以获得一个非常适合 verifier 的证明，该证明适合比特币验证。

我们的比特币 STARK 验证器实际上比我们在本文中介绍的要多得多优化。在这里，我们为感兴趣的读者概述它们，但它们都属于使用递归将证明从 prover 高效转换为 verifier 高效的想法。

切换哈希函数。 我们使用 Poseidon 哈希函数生成第一个 Plonk 证明，这对于递归来说很好，但是在比特币上评估 Poseidon 哈希函数（即使使用 OP_CAT）的效率不是很高。

我们所做的是，在最后一个证明中，这是多层递归的结果，我们不再使用 Poseidon，而是切换到使用 SHA-256 作为哈希函数。因此，比特币 STARK 验证器（用比特币脚本实现并使用比特币执行环境）可以简单地使用比特币中可用的 SHA-256 操作码（取决于 OP_CAT 的可用性，如果没有它，这些操作码就不会那么有用）。

尽管我们一直专注于 OP_CAT，并且现有的构造依赖于 OP_CAT，但这种切换哈希函数的能力对于在 BitVM 中验证 STARK 证明也很有用。目前，在 BitVM 中，我们主要使用 Blake3 哈希函数，因为在比特币脚本中实现它证明是最简单的。递归还可以直接将哈希函数从 Poseidon 更改为 Blake3。

增加 blowup 系数。 我们之前在这篇文章和第一部分文章中提到过，人们可以在prover效率和verifier效率之间进行权衡，并且可以通过多种方式来实现。最简单的方法是增加 blowup 系数。

例如，为了获得最高效的 prover，我们使用低至 2 的 blowup 系数。这将需要在 STARK 证明验证协议中进行大约 80 个 FRI 查询，以达到所需的安全性级别。但是，我们可以在保持相同安全级别的情况下更改此系数。

• 如果我们将 blowup 系数从 2 增加到 4，我们只需要 40 个 FRI 查询。

• 如果我们将其增加到 8，我们需要 34 个 FRI 查询。

• 如果我们将其增加到 16，我们需要 20 个 FRI 查询

• 如果我们将其增加到 32，我们需要 16 个 FRI 查询。

• 如果我们将其增加到 512，我们只需要大约 9 个 FRI 查询。

尽管 verifier 效率取决于许多因素，但从大致数字来看，FRI 查询的数量越少，verifier 就越快。请注意，这是以 prover 速度变慢为代价的。例如，当我们使用 512 的 blowup 系数时，与 2 的 blowup 系数相比，prover 的工作量是 256 倍——这仅在我们专门平滑证明以使其非常适合 verifier 时才有用——例如，在以太坊或比特币上将其验证为最后一层。在这些情况下，由于链上验证可能涉及昂贵的费用，因此从经济上来说，值得增加 prover 时间（仅在最后的递归证明中）以获得更好的性能。在实践中，这只需要大约几百秒的计算时间。

没有 Poseidon 的最后一层递归。 请注意，verifier 成本取决于许多因素。但是，证明系统中列的数量也是其中之一。

在第一部分文章中，我们介绍了我们的递归证明系统，该系统由 Plonk 组件的 30 列和 Poseidon 组件的 96 列组成。一个自然的问题是我们是否可以在最后一层删除 Poseidon 组件（知道这将使 prover 速度变慢，作为成本），以便减少列数。

这正是我们为比特币 STARK 验证器所做的事情，在最后一层，我们仅使用 Plonk 组件，但是此 Plonk 组件有额外的修改（可以在 这里 找到），以便在没有 Plonk 的情况下更有效地处理 Poseidon。当然，这样做会增加 Plonk 组件中的行数，并且它会随着整个证明验证过程中哈希函数调用次数的增加而增长——正如我们所看到的，主要是来自去承诺和 folding 中使用的 Merkle 树。

Poseidon 操作的数量可能会成为 prover 效率的瓶颈，实际上，也会成为 verifier 效率的瓶颈。因此，我们使用一种新技术将大部分哈希操作委托给比特币脚本，这在评估某些哈希函数（如 SHA-256）时可能更有效——当然，不是 Poseidon。因此，我们将再次切换哈希函数，使“倒数第二个”证明使用 SHA-256 而不是 Poseidon，然后，当最后一层验证此证明时，它会将 SHA-256 哈希操作委托给比特币。我们发现，这种方法有助于我们更好地管理比特币 STARK 验证成本。

值得指出的是，这种方法也有助于以太坊上的 STARK 验证器。

结论

在本文中，我们从上一篇文章继续，并描述了我们用于 Stwo 的递归证明系统的 Poseidon 组件。我们展示了为什么专用的 Poseidon 组件可以带来更好的性能，并用具体的评估来支持它。

我们正在与 StarkWare 合作，将本文构建的递归证明技术 (用于比特币 STARK 验证器) 集成到 StarkWare 的 Stwo 证明系统中，以便结算到以太坊和比特币，包括基于 BitVM 的比特币桥。

在 l2iterative.com 和 Twitter @ l2iterative 查找 L2IV

作者：Weikeng Chen，L2IV 研究合伙人

• 原文链接： l2ivresearch.substack.co...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～