用四种不同语言编写零知识证明和电路 - 两个向量的点积

概述

我们将使用 Zero Knowledge Proofs (ZKP) 在 Circom 和 Halo2 中实现两个大小为 N 的向量的点积。根据 k12.libretexts.org，两个大小为 N 的向量 A 和 B 的点积为：

A.B = a1*b1 + a2*b2 + ... + aN*bN

• 概述
• 零知识证明的流程
• 两个向量的点积的 Circom 电路
  • Circom 设置和安装
  • Circom 安装依赖
  • 安装 Circom
  • 安装 Snarkjs
  • 实现两个向量的点积的 Circom 电路
• 两个向量的点积的 Halo2 电路
  • Halo2 设置和安装
  • 实现两个向量的点积的 Halo2 电路
  • 什么是可信设置，为什么在现实应用中是必要的？
• 两个向量的点积的 Noir 电路
  • 安装 Noir
  • 实现两个向量的点积的 Noir 电路

零知识证明的流程

以下图描述了创建零知识证明系统的典型流程。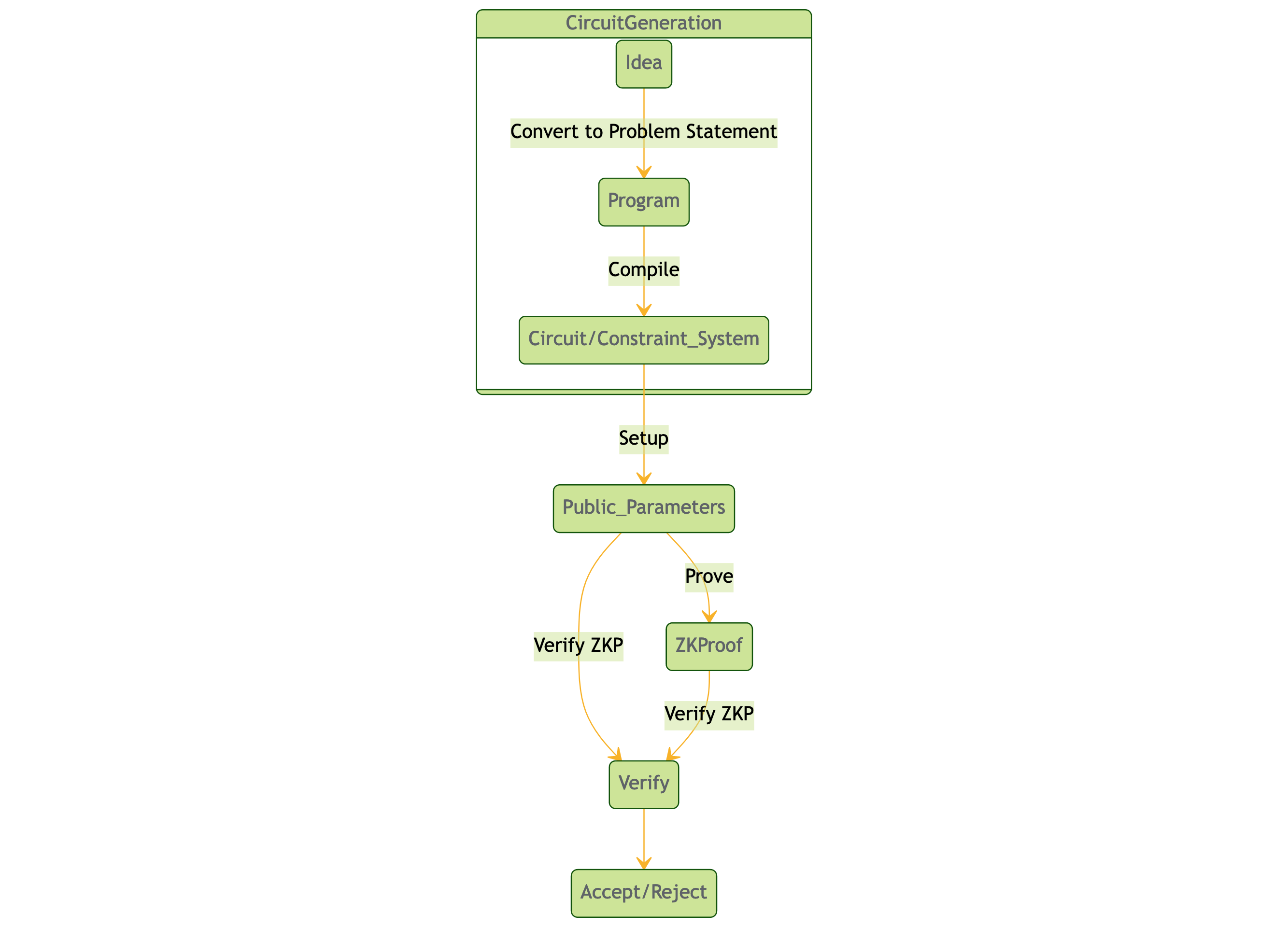

要使用不同的库（如 Circom、Noir 和 Halo2）创建零知识证明和电路，请遵循以下步骤：

1. 定义问题：确定要使用零知识证明来证明的问题。例如，证明你是前100个Uniswap流动性提供者的成员，而没有透露任何额外信息，或者证明你在智能合约中发现了一个关键错误而没有透露任何额外信息。
2. 选择合适的 ZKP 库：选择适合你需求的库，例如 Circom、Noir 或 Halo2 等。每个库都有自己的一套功能和权衡：
   • Circom：旨在以简单直观的方式创建电路的特定领域语言（DSL）。它对创建 zk-SNARK 电路很有用。有关 Circom 的更多详细信息，请访问 官方文档。
   • Noir：一种高层次、通用的零知识证明语言。它易于理解，并且生态系统正在不断发展。有关 Noir 的更多详细信息，请访问 官方文档。
   • Halo2：一种构建无可信设置的 zk-SNARKs 的库，提供比其他某些库更安全和更高效的替代方案。有关 Halo2 的更多详细信息，请访问 官方文档。
3. 创建电路：使用所选库设计表示问题的电路。这涉及定义输入、输出和必须满足的限制条件，以确保证明有效。
4. 生成证明：使用库的工具生成零知识证明，以证明该语句是真实的，而不公开任何额外信息。
5. 验证证明：实现验证过程，以确保证明有效且语句真实，而不泄露任何额外信息。

两个向量的点积的 Circom 电路

在这个例子中，我们将研究如何为两个向量的点积编写 Circom 电路，创建零知识证明并验证证明而不透露任何额外信息。

Circom 设置和安装

有关安装 Circom 生态系统的完整最新文档，请访问 这里。较旧版本的 Circom 也可以从 旧版本 Circom 存储库 安装。

Circom 安装依赖

Circom 编译器是用 Rust 编写的。要使 Rust 在你的系统上可用，可以安装 rustup。如果你使用的是 Linux 或 macOS，请打开终端并输入以下命令：

curl --proto '=https' --tlsv1.2 https://sh.rustup.rs -sSf | sh

你还需要安装最新版本的 Node.js（或 yarn）。可以从 这里 安装它们。

安装 Circom

首先，克隆 circom 存储库：

git clone https://github.com/iden3/circom.git

进入 circom 目录并使用 cargo build 进行编译：

cargo build --release

安装过程大约需要 3 分钟。当命令成功完成时，它会在 target/release 目录中生成 circom 二进制文件。可以按如下方式安装此二进制文件：

cargo install --path circom

之前的命令会将 circom 二进制文件安装在 $HOME/.cargo/bin 目录中。

安装 Snarkjs

你可以使用以下命令安装 snarkjs：

npm install -g snarkjs

实现两个向量的点积的 Circom 电路

要在 Circom 中实现两个向量的点积，我们可以遵循以下步骤：

1. 定义两个大小为 N 的向量 A 和 B。
2. 定义一个变量来存储点积。
3. 通过将 A 和 B 对应组件相乘并相加来计算点积。
4. 输出点积。

以下是 Circom 中的代码示例：

template DotProduct(N: number) {
    signal A[N];
    signal B[N];
    signal result;

    component multiply[N];
    component add[N-1];

    for (i = 0; i < N; i++) {
        multiply[i] A[i] * B[i] -> add[i];
    }

    for (i = 0; i < N-1; i++) {
        add[i] + add[i+1] -> add[i+1];
    }

    add[N-2] -> result;
}

在上述代码中，我们定义了两个输入信号 A 和 B，大小为 N，它们表示这两个向量。我们还定义了一个输出信号 result，用于存储点积。

接下来，我们定义了两个组件 multiply 和 add。multiply 组件将 A 和 B 的对应组件相乘，而 add 组件将它们相加。我们使用循环将 multiply 组件的输出连接到 add 组件的输入。我们还使用循环将 add 组件的输出相互连接，直到到达最终的输出信号 result。

要使用此模板，我们可以简单地实例化它并为 A 和 B 信号提供值：

template Main() {
    signal A[4] = [3, -5, 4, 2];
    signal B[4] = [2, 6, 5, 1];
    signal result;

    DotProduct(4)()
        .A(A)
        .B(B)
        .result(result);

    print(result);
}

在上述代码中，我们定义了两个输入信号 A 和 B，大小为 4，并定义了一个输出信号 result。然后我们实例化 DotProduct 模板，大小为 4，并将其 A 和 B 信号连接到相应的输入信号。我们还将其 result 信号连接到我们的输出信号。最后，我们打印 result 信号。

两个向量的点积的 Halo2 电路

在这个例子中，我们将研究如何为两个向量的点积编写 Halo2 电路，创建零知识证明并验证证明而不透露任何额外信息。

Halo2 设置和安装

Halo2 需要最新版本的 Rust。有关使用 Halo2 进行开发的更多信息，请访问 Halo2 官方文档。

实现两个向量的点积的 Halo2 电路

要在 Halo2 中实现两个向量的点积，我们首先需要在 Halo2 中定义我们的电路。以下是此代码：

use halo2::{
    circuit::{Layouter, SimpleFloorPlanner},
    plonk::{Circuit, ConstraintSystem, Error},
    poly::Rotation,
};

// 定义电路结构
#[derive(Debug)]
struct DotProduct<'a> {
    a: &'a [u64],
    b: &'a [u64],
    result: &'a mut [u64],
}

// 实现电路特征
impl<'a> Circuit<SimpleFloorPlanner> for DotProduct<'a> {
    type Config = ();
    type FloorPlanner = SimpleFloorPlanner;

    fn without_witnesses(&self) -> Self {
        DotProduct {
            a: self.a,
            b: self.b,
            result: &mut [0; N],
        }
    }

    fn configure(
        _config: Self::Config,
        meta: &mut ConstraintSystem<SimpleFloorPlanner>,
    ) -> Result<(), Error> {
        // 定义输入信号 A 和 B
        let a = meta.advice_column();
        let b = meta.advice_column();

        // 定义用于乘法的中间信号
        let mul = (0..N)
            .map(|_| meta.advice_column())
            .collect::<Vec<_>>();

        // 定义用于加法的中间信号
        let add = (0..N - 1)
            .map(|_| meta.advice_column())
            .collect::<Vec<_>>();

        // 定义输出信号 result
        let result = meta.advice_column();

        // 将输入信号限制为提供的值
        for (i, &value) in self.a.iter().enumerate() {
            meta.enable_constant(a[i], value.into())?;
        }
        for (i, &value) in self.b.iter().enumerate() {
            meta.enable_constant(b[i], value.into())?;
        }

        // 将乘法信号限制为 
        // A 和 B 的相应组件的乘积
        for i in 0..N {
            meta.multiply(
                Rotation::prev(),
                &[a[i], b[i]],
                mul[i],
            )?;
        }

        // 将加法信号限制为 
        // 相应乘法信号的和
        for i in 0..N - 1 {
            meta.add(
                Rotation::cur(),
                &[mul[i], mul[i + 1]],
                add[i],
            )?;
        }

        // 将输出信号限制为最后一个加法信号
        meta.copy(
            Rotation::cur(),
            add[N - 2],
            result,
        )?;

        // 将输出信号限制为提供的值
        for (i, &value) in self.result.iter().enumerate() {
            meta.constrain_equal(result, value.into())?;
        }

        Ok(())
    }
}

在此代码中，我们定义了电路结构体 DotProduct，其中包含输入信号 a 和 b，以及一个输出信号 result。我们还为我们的电路实现了 Circuit 特征，定义电路的构造和约束方式。

我们使用 meta.advice_column() 定义输入信号 a 和 b，它在电路中创建一个新的建议列。我们还定义了中间信号 mul 和 add，用于执行乘法和加法操作。最后，我们定义了输出信号 result。

我们使用 meta.enable_constant() 限制输入信号为提供的值，接着使用 meta.multiply() 限制乘法信号，确保 a 和 b 的相应组件的乘积限制到相应的乘法信号。然后我们使用 meta.add() 限制加法信号，将相应的乘法信号的和限制为相应的加法信号。最后，使用 meta.copy() 将输出信号限制为最后一个加法信号，并使用 meta.constrain_equal() 将其限制为提供的值。

要使用此电路，我们可以实例化它并提供 a 和 b 的值，以及一个空向量作为 result。然后，我们可以使用 Prover::prove() 创建一个证明，并使用 Verifier::verify() 验证该证明。以下是示例：

use halo2::{
    dev::MockProver,
    plonk::{Circuit, ConstraintSystem, Verifier},
};

// 定义我们向量的大小
const N: usize = 4;

// 定义我们的主函数
fn main() {
    // 定义输入信号 A 和 B
    let a = [3, 5, 4, 2];
    let b = [2, 6, 5, 1];

    // 定义输出信号 result
    let mut result = [0; N];

    // 实例化电路
    let circuit = DotProduct {
        a: &a,
        b: &b,
        result: &mut result,
    };

    // 创建证明
    let prover = MockProver::run(N, &circuit, vec![]).unwrap();
    let proof = prover.proof;

    // 验证证明
    let verifier = Verifier::new(N, &circuit, &proof).unwrap();
    assert!(verifier.verify().is_ok());

    // 打印结果
    println!("{:?}", result);
}

在此代码中，我们定义了输入信号 a 和 b 以及输出信号 result。然后实例化 DotProduct 电路并提供这些值。我们使用 MockProver::run() 创建证明，这模拟了电路执行并生成一个证明。接着使用 Verifier::new() 和 verify() 验证证明。最后，打印 result。

请注意，在此示例中，我们使用 MockProver 来生成和验证证明。在实际应用中，我们将需要使用可信设置来生成证明和验证密钥，并使用这些密钥生成和验证证明。我们还需要确保电路的输入和输出被正确加密和解密，以防止信息泄露。然而，这些细节超出了本示例的范围。

什么是可信设置，为什么在现实应用中是必要的？

可信设置是某些零知识证明系统（包括 Halo2）中使用的一个过程，用于生成生成和验证证明所需的密钥。可信设置涉及一组受信任的个人或实体，他们共同生成并销毁用于生成密钥的秘密值。在生成密钥后，秘密值被销毁，这样没有人可以获取并使用它生成假证明。

在实际应用中，可信设置是必要的，因为它确保证明和验证密钥的生成方式是安全且不偏不倚的。如果没有可信设置，攻击者可能会潜在地生成他们自己的密钥，并使用这些密钥生成被系统接受的假证明。可信设置确保密钥的生成与攻击者无关，并且攻击者无法获取用于生成密钥的秘密值。

在 Halo2 中，可信设置涉及生成电路列的随机排列，并使用此排列生成密钥。该排列是使用多方计算协议生成的，其中每个参与者贡献一个随机值，这些值组合以生成最终的排列。该排列能够确保电路的列混合在一起，以防止攻击者通过观察密钥获知电路的任何信息。

一旦可信设置完成，证明和验证密钥将分发给系统的用户，用户可以使用这些密钥生成和验证证明。用户不需要信任彼此或系统，因为这些密钥是以安全和不偏不倚的方式生成的。然而，用户必须确保电路的输入和输出被正确加密和解密，以防止信息泄露。

总之，可信设置是用于为零知识证明系统生成证明和验证密钥的一个过程，在实际应用中是必需的，确保以安全和不偏不倚的方式生成密钥。

两个向量的点积的 Noir 电路

在这个例子中，我们将研究如何为两个向量的点积编写 Noir 电路，创建零知识证明并验证证明而不透露任何额外信息。

有关 Noir 编程语言的更多详细信息，请访问 官方文档。

安装 Noir

Noir 是基于 Rust 的语言。你可以访问官方文档以获取 安装说明。

实现两个向量的点积的 Noir 电路

要在 Noir 中实现两个向量的点积，我们首先需要在 Noir 中定义我们的电路。以下是代码示例：

// Noir 没有内置的点积函数，因此我们创建一个
fn dot_product(vect_A: [field], vect_B: [field]) -> field {
    let mut result: field = 0;
    let N = vect_A.len();

    for i in 0..N {
        result += vect_A[i] * vect_B[i];
    }

    return result;
}

// 示例用法
fn main() {
    let vect_A: [field] = [1, 2, 3, 4];
    let vect_B: [field] = [5, 6, 7, 8];

    let result: field = dot_product(vect_A, vect_B);

    // 结果应该是 70 (1*5 + 2*6 + 3*7 + 4*8)
    assert_eq!(result, 70);
}

1. 定义了 dot_product 函数，接收两个输入参数 vect_A 和 vect_B，这两个参数都是 field 类型的数组（field 是 Noir 中代表有限域元素的类型）。该函数返回一个 field。
2. 在 dot_product 函数内部，初始化一个可变变量 result，其值为 0，并将 vect_A 的长度存储在变量 N 中。
3. 使用循环遍历两个输入数组的索引，从 0 到 N-1。在每次迭代中，将两个数组的对应元素相乘并累加到 result 中。
4. 函数返回 result 作为 dot_product 函数的输出。
5. 主函数演示了如何使用 dot_product 函数。定义了两个数组 vect_A 和 vect_B，并通过 dot_product 函数计算它们的点积。
6. 最后，使用断言检查 result 是否等于 70，这是预期的点积值 (1*5 + 2*6 + 3*7 + 4*8)。

以下步骤将构建 ZKP 程序并创建证明，验证证明而不透露任何额外信息。

• 构建: nargo check
• 证明: 在 Prover.toml 中输入输入并运行 nargo prove p -v。或者运行 nargo prove --show-output p 显示打印日志。
• 验证: nargo verify p

• 原文链接： github.com/thogiti/thogi...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～