如何在不 REKT 情况下优化Gas消耗 第一部分
- Certora
- 发布于 2023-04-27 16:27
- 阅读 1247
本文探讨了去中心化金融(DeFi)领域中的智能合约安全性问题,并介绍了一种新的工具——等价检查器(Equivalence Checker),旨在帮助开发者在安全性、开发时间和Gas消耗之间取得更好的平衡。文章深入分析了智能合约开发面临的三大挑战以及使用等价检查器进行对比验证的实例,以确保代码的功能等价性。
简介:分布式金融三难问题
越来越多的人达成共识,去中心化金融(DeFi)领域必须克服的关键障碍之一是智能合约的安全问题。
事实上,当关于欺诈和损失的报道主导新闻周期时,更广泛的主流采用仍然是一个遥不可及的前景,更不用说与目前的金融服务和投资银行巨头如 Visa、J.P. Morgan 和 Goldman Sachs 进行真正的竞争。
与社区外的许多人所说的相反,这个问题并不只是因为过度炒作的项目有着极端的截止日期或是一种 cowboy coding 文化的创业公司。
这些众所周知的因素在某些情况下确实存在,并且它们无疑会造成影响,但将责任完全归咎于它们的脚下是完全荒谬的,任何在区块链社区中的人都可以告诉你。
其实情况要糟糕得多,远远更糟。
这是因为开发 DeFi 产品是一个欺骗性的深度工程问题——用 Solidity 撰写一个(大致上)符合你需求的智能合约是容易的,但要做到这一点得当却很难。就像 Vitalik Buterin 著名的 区块链三难问题 一样,智能合约开发的过程也受到三个独立且经常相互冲突的目标的指导:

- 最小化 gas 消耗。 就像在高频交易中,似乎“微不足道”的优化可能会对 gas 成本产生深远的影响,从而影响可用性。在用尽常规的“把戏”后,改进各种操作的 gas 成本通常需要用汇编语言而不是 Solidity(或 Viper)编写,或找到一种聪明的技巧来计算非线性和计算开销大的功能的近似值。
- 最大化安全性。 像硬件一样,智能合约在设计上是不可变的,这意味着在开发过程中引入的任何漏洞都将长期存在。诚然,存在可升级合约并可以绕过不可变性。然而,它们的存在引入了另一种权衡:用户永远无法确定他们交互的合约不会改变,每次升级都伴随着引入新漏洞的风险。加上 DeFi 协议处理大量资金的现实和 EOA 地址与现实身份的固有解耦(以及“代码即法律”的理念),这些现实可能使代码中的任何漏洞都变得极其危险且代价高昂。尤其是,这意味着必须对舍入错误、边缘情况和数学设计问题非常小心。

- 最小化上市时间。 这是任何软件项目中一个紧迫的问题,但在极具竞争力和高度波动的去中心化金融世界中尤为如此。不幸的是,即使一个人同时实现了 gas 优化和安全性的目标,明显地,在每一步施加的额外检查也会大大减缓开发过程。

开发周期中的形式验证
为了帮助开发者在不妥协任何这三项要求之间达到更好的平衡,Certora 开发了一种名为 Equivalence Checker 的新工具。与专注于测试和安全性的 Certora Prover 不同,这种轻量级形式验证允许 DeFi 程序员比较用以下方式编写的相同数学公式的不同版本:
- 低级(Yul 或汇编)
- 高级(Solidity)
- 纯逻辑(编码在 Certora Verification Language 或简称为 CVL 中)
并表明它们是 等价的(有关更多信息,请参见下文)。它旨在作为一项快速开发工具,贯穿项目的整个生命周期,并有助于安全性、开发时间和 gas 消耗。
本文的其余部分将演示此新工具在实际案例中的工作流程。我们解释 Equivalence Checker 的不同模式,并演示它如何能够立即检测出一个著名的旧漏洞以及一个新的、以前未发现的漏洞(注:读者应注意,这个选择的是一个_低严重性_的漏洞,仅用于教学目的。在这篇博客的续集中,我们将揭示并分析一个更复杂的案例,其中检测到使用 Equivalence Checker 的 高严重性 漏洞——请继续关注!)
但首先,
“功能等价性”究竟是什么意思?
一个 Solidity/Yul 函数被称为 纯 如果它不读取或修改状态(但是它可以在发生错误时回滚潜在的状态变化)。它可以有多个输入和输出值。例如,以下函数是纯的:
function safeAdd(uint a, uint b) public pure returns (uint c) {
c = a + b;
require(c >= a);
}我们将说两个纯函数 f(…) 和 g(…) 是 等价的,如果:
- 它们具有相同的输入/输出变量。
- [假设 1 成立:] 对于给定的输入值元组 -
(a) f 仅在 g 回滚时回滚。
(b) [假设 f 和 g 没有回滚:] f 和 g 的返回值是相同的。
当然,这一定义可以扩展到 EVM 字节码的适当片段,并在以太坊 黄皮书 的形式中进行精确定义。(纯函数和逻辑公式之间的等价性相似,但稍微更微妙,通过下面的第二个例子解释最好)。
现在我们已经正确定义了等价性,是时候开始认真讨论了。
背景:实现定点除法
众所周知,以太坊虚拟机(EVM)原生只支持两种数据类型:256位 字和 8位 字节。此外,大多数 EVM 操作码一次处理的是字大小的数据块,包括所有的数学操作。因此,以太坊中基本上只有两种数值数据类型:
- 有符号的 256 位整数。
- 无符号的 256 位整数,
它们分别在 Solidity 中用 uint256 和 int256 数据类型表示。
这很不幸,因为几乎任何金融应用都需要实现对分数算术的某种支持。处理这种问题的方法有几种,但在 DeFi 应用中(绝大多数)最流行的是定点数。这基本上是分母为预定义常数的简单分数,通常是 2(“二进制”)或 10(“十进制”)的幂。在十进制情况下,标准分母选择是 10¹⁸(称为“wad”)或 10²⁷(称为“ray”)。因此,现有的 Solidity 定点库通常将 wad 表示为 256位整数。这在加法和减法时相对简单,但在执行乘法或除法时,必须重新缩放结果以获得正确的答案。
例如,
1.5 * 2.7 == 4.05
// 普通整数算术会增加数量级:
150 * 270 == 40500
// Wad 算术并不会增加数量级:
wadMul(1.5 ether, 2.7 ether) == 4.05 ether考虑以下测试用例。我们想编写一个函数 wadDiv,将两个 wad 相除,将半 wad 及以上 四舍五入 到最接近的 wad。这类算术函数在 DeFi 中非常常见。它们有必要考虑整数算术的正常行为和十进制算术的实际工作方式之间的差异。
第 1 步:测试代码
首先,我们考虑以下在 Solidity 中编写的 wadDiv 参考实现:
uint256 internal constant WAD = 1e18;
function wadDivSol(uint256 a, uint256 b) public pure returns (uint256 c)
{
c = (a * WAD + (b/2)) / b;
return c;
}为了优化它,我们稍微尝试了一下汇编,并创建了以下暂时的 Yul 版本:
function wadDivAsm(uint256 a, uint256 b) public pure returns (uint256 c)
{
assembly
{
if iszero(iszero(gt(a, div(sub(not(0), div(b, 2)), WAD))))
{ revert(0, 0) }
c := div(add(mul(a, WAD), div(b, 2)), b)
}
}确实,我们看到 gas 成本大幅降低:Solidity 版本计算所需的 ~860 gas,而汇编版本仅消耗 ~140 gas。
问题。 这有效吗(即这两个函数是等价的吗)?
与其绞尽脑汁寻找回答,Equivalence Checker 的通用规则模板立即产生以下两个规则,使用 CVL( Certora Verification Language)写成,并提交给 Prover 进行形式验证。
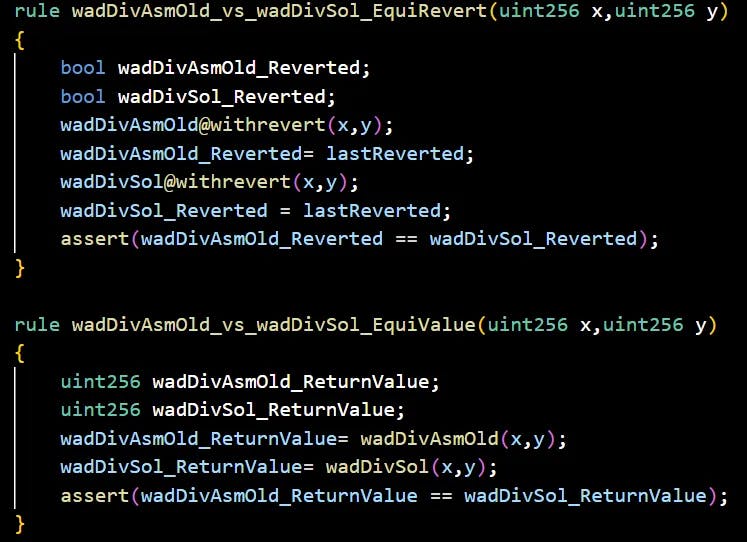
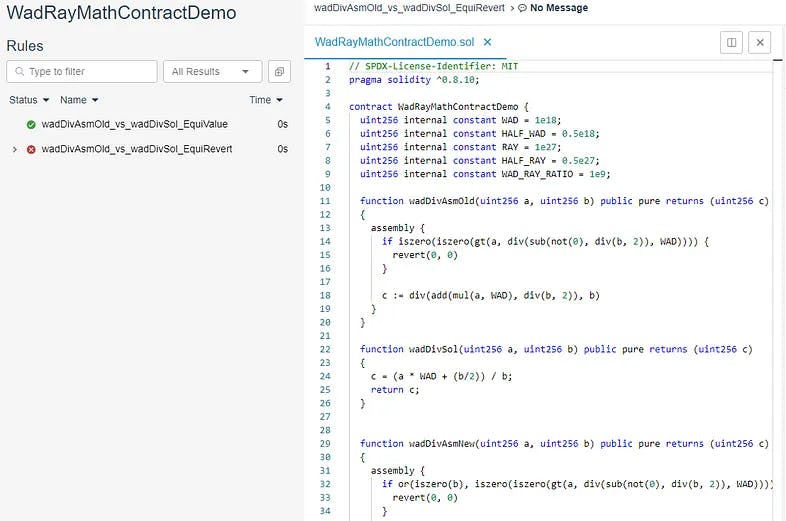
几乎立刻,prover 检测到两个回滚条件之间的差异:
并得出以下反例:
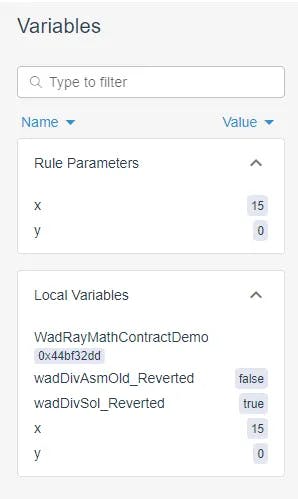
(为什么?因为 Yul 中的除零返回零而不是回滚!请查看链接的 推特线程 以获取详细讨论)
第 2 步:测试逻辑
假设我们现在修复了这个漏洞并编写了一个新的 Yul 版本:
function wadDivAsmNew(uint256 a, uint256 b) public pure returns (uint256 c)
{
assembly
{
if or(iszero(b), iszero(iszero(gt(a, div(sub(not(0), div(b, 2)), WAD)))))
{ revert(0, 0) }
c := div(add(mul(a, WAD), div(b, 2)), b)
}
}问题。 我们完成了吗?
好消息: 运行 Equivalence Checker 现在表明它与 Solidity 版本相同!
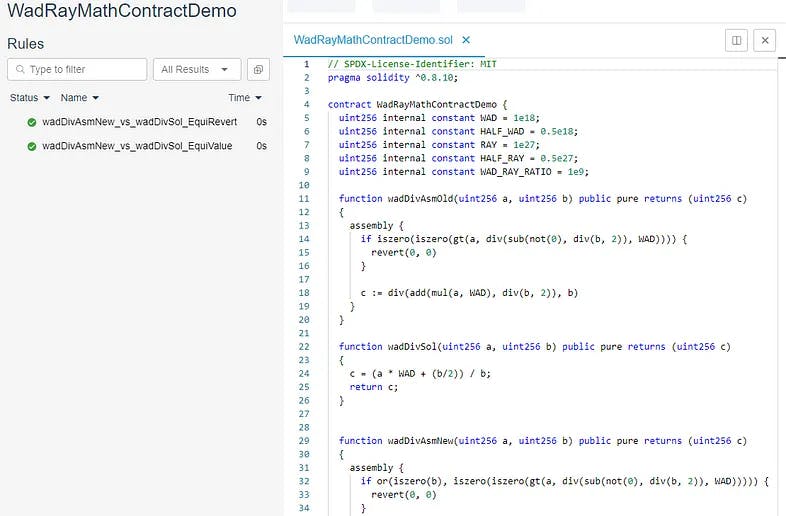
坏消息: 等等……因为我们最初的 Solidity 版本是错误的。
要看到这一点,我们需要在不同的配置中运行 Equivalence Checker。在前一段中,我们解释了如何使用 Equivalence Checker 比较代码( wadDivAsmOld)与代码( wadDivSol/wadDivAsmNew)。
现在我们需要比较一段代码( wadDivSol),它在 EVM 上执行某一特定的数学计算,与描述其行为的两个数学函数:
- _
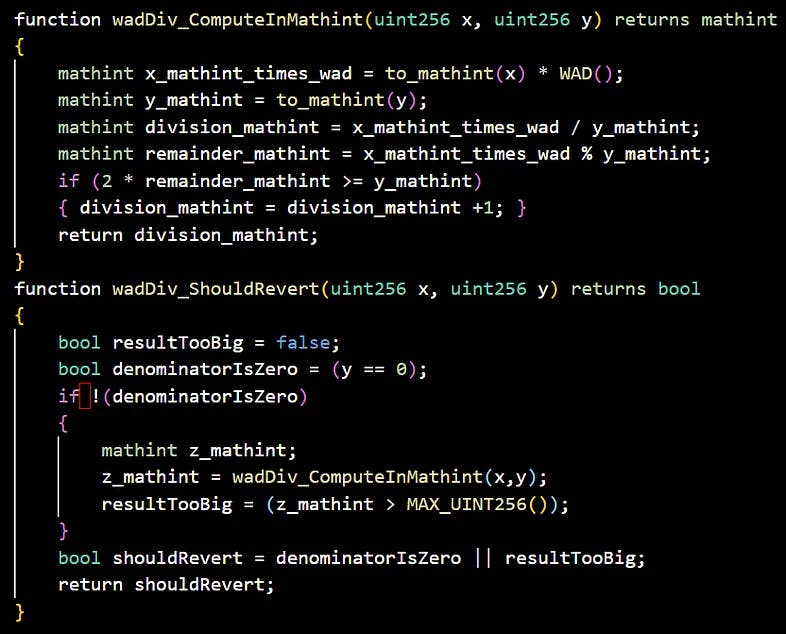
wadDiv_ShouldRevert_ —— 编码期望的 回滚条件,即这是一个布尔值函数,接受与wadDivSol相同的输入参数,并且当且仅当 连执行wadDivSol的 EVM 结果应该为回滚时返回 true。在我们的情况下,我们希望wadDivSol仿佛仅当分母为零或结果大于2²⁵⁶-1(可以存储在uint256中的最大整数)时发生回滚,从而导致整数溢出。 - _
wadDiv_ComputeInMathint_ —— 其接受与wadDivSol相同的输入参数,并对输出进行编码,作为在整数上计算的公式。
用 CVL 编写,这两个函数的规范为 -
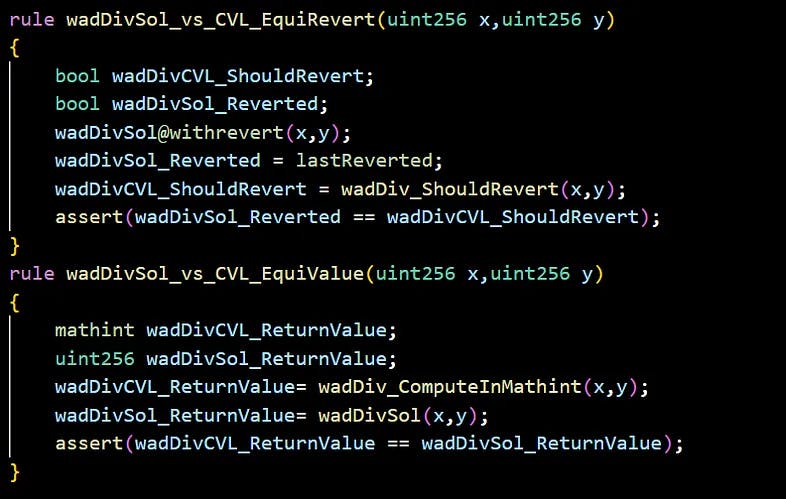
在这种情况下,等价性测试由检查以下两个规则是否成立:
它们意味着什么?
- 呃,第一个规则正是它看起来的那样。它说明 _
wadDiv_ShouldRevertreverts当且仅当wadDivSolreverts_。 - 第二个规则稍微微妙一点。它声明在相同的输入下,
wadDivSol和wadDiv_ComputeInMathint返回相同的uint256值 前提是wadDivSol未回滚(注意第二条规则中缺乏 @withrevert 修饰符)。
运行 Prover 结果为反例:
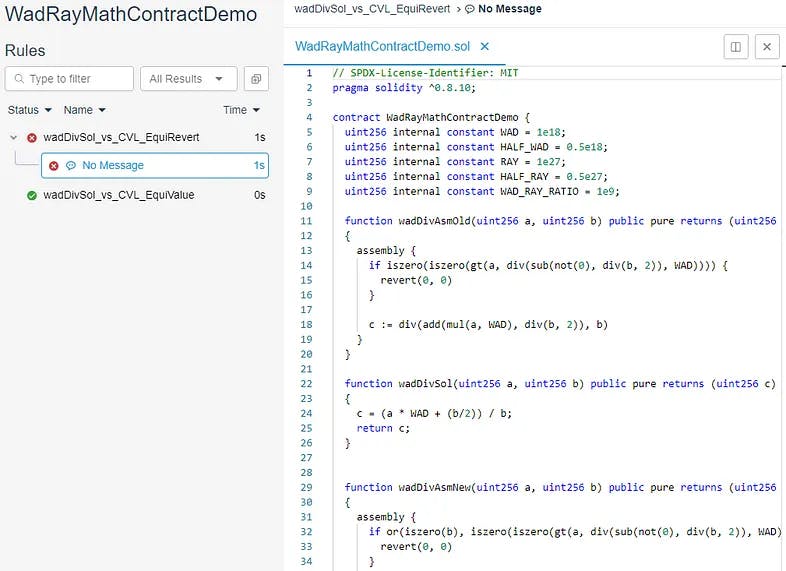
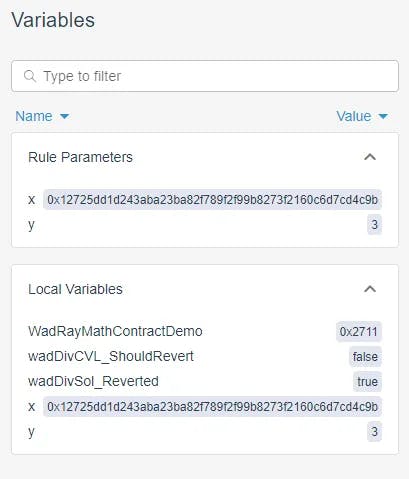
实际上,在将这些值转换为十进制后,我们得到:
X (作为 WAD) = 1766847064778384331350144565521302847.177628462396921805
Y (作为 WAD) = 0.000000000000000003
=> X/Y (作为 WAD) = 588949021592794777116714855173767615725876154132307268.333333333333333333这仍然在范围内,可以用 uint256 类型表示。因此,我们发现我们写的 Solidity 版本回滚“过于急躁”,即我们选择的实现方式导致了不必要的回滚。
结论
Equivalence Checker 是一个灵活、易于使用的 CLI 工具,它允许用户比较两段代码或实现与规范之间的功能等价性。其目的是在不妥协安全性的情况下,加快代码开发并提高 gas 效率。当前原型版支持 Yul、Solidity 和 CVL。预计将于2023年第二季度发布。

未来规划的版本可能允许 Solidity/Yul 和 Vyper(甚至 Cairo)之间的比较。
我希望你喜欢这个教程并探索工具的能力。我们非常希望得到开发者和用户的反馈和改进建议。如果你有任何问题或建议,请在下面评论。
最后,正如我们所提到的,这篇博客仅仅是一个系列的第一部分,因此请继续关注更多内容!
- 原文链接: certora.com/blog/optimiz...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- Uniswap v3 白皮书与代码解析 43 浏览
- 使用 OpenZeppelin 开发安全的智能合约 124 浏览
- 使用OpenZeppelin Contracts设置Solidity智能合约项目 115 浏览
- OpenZeppelin Skills 发布 200 浏览
- 在 Arbitrum 上使用 Stylus 智能合约项目 117 浏览
- OpenZeppelin Contracts for Stellar 项目设置 122 浏览

