宇宙中的电子数量比512位质数多吗?
- asecuritysite
- 发布于 2025-03-22 12:14
- 阅读 1616
文章探讨了宇宙中电子数量与不同位数的质数数量的对比,指出质数的数量远大于电子的数量,特别是在密码学中使用的2048位质数。文章介绍了评估质数数量的方法,包括使用Sieve of Eratosthenes算法和Riemann R函数,并提供了Python和PowerShell代码示例来生成和测试质数,强调了质数在公钥加密中的重要性以及生成大质数的必要性。

宇宙中的电子比 512 位素数更多吗?
答案是否定的!
宇宙中大约有 8.37x10⁷⁷ 个电子。而且,虽然这个数字可能看起来很大,但估计的 512 位素数(大约 160 位数字)的数量是 [ 这里]:
18906370642694533330255267422559435438516148269380861172414282021437571915512683767157742768034244490543655250659082340701872652735175220791902826659840
也就是 1.5x10¹⁵¹。事实上,对于 RSA,我们可以使用 2,048 位素数来用于 4096 位 RSA,并且作为估计,素数的总数是 [ 这里]:
11385172270258672953764793456388645214256740287188220237389104580032209792659193924101416597006335941813038755260878001567334933908725291403697392808828239764599609819731878152305734495554617798558938055499227953935671432466474597689981539404264108325526516247781591774691266828619629734180673225660241271543591391989708758169413624895421128195230477399212718531210499701272562448816178087091221785420932500650269661768355526533958545122702304553518111237381614796970882146854046586446112589627992086028076057005913397168273375915681546605655773788353223659319186860982233577649003599445529974508879522956597788672
大约是 1.1x10¹⁰²³。因此,宇宙中的素数比电子多。
我们的许多公钥方法都依赖于素数,因为它们具有出色的属性,包括对数字执行数学运算的方式,但使用有限域来约束它们(我们的最大数字是小于素数的数字)。例如,RSA 的难点在于将 N 的值分解为创建 N 的两个素数。如果找到这些素数,我们可以很容易地找到与加密密钥关联的解密密钥 [这里]。
希腊数学家欧几里得证明了没有“最大”素数,我们可以无限延伸,永远找不到最后一个素数。
因此,如果我们选择一个特定大小的素数,我们如何知道入侵者必须搜索多少个素数才能找到我们使用的一个(或多个)?如果我们选择一个小的值,例如 0 到 15 之间(4 位),则不会很困难,因为素数将是:
2, 3, 5, 7, 11, 13, 17 和 19
但是,如果我们选择 10⁵⁰,我们如何估计有多少个素数呢?嗯,在密码学中,我们可以使用 pi ( x) 函数来估计 0 到 x 之间的素数数量。
计算 π(x) 最简单的方法之一是生成它们并计数。以下代码是一个筛选法,源自希腊数学家埃拉托斯特尼定义的方法。通过这种方法,我们过滤掉每个素数的倍数 [这里]:
## https://asecuritysite.com/encryption/nprime
import sys
from mpmath import *
start = 0
end = 100
if (len(sys.argv)>1):
start=int(sys.argv[1])
if (len(sys.argv)>2):
end=int(sys.argv[2])
def sieve(n):
"""
Generate the primes less than or equal to n using the sieve of
Eratosthenes.
"""
primes, sieve = [], [True] * (n + 1)
for p in range(2, n + 1):
if sieve[p]:
primes.append(p)
for i in range(p * p, n + 1, p):
sieve[i] = False
return primes
def pi(x):
"""Calculates the number of primes less than or equal to x."""
return len(sieve(x))
print ("Range from",start,"to ",end)
est= pi(end)-pi(start)
print ("Estimation of primes:\t\t\t",est)
print ("Possibility of finding prime (%):\t",est/float(end-start)*100)
print ("\n----- Using Riemannr method to estimate")
print ("Estimation is:\t",int(riemannr(end)))
print ("\nRange\tEst number of primes")
val=1
for x in range(1,31):
val=val*10
print ("10^",x,"\t","{:,}".format(int(riemannr(val))))使用的一种方法是使用 Schoenfeld 不等式计算素数计数函数 π(x):
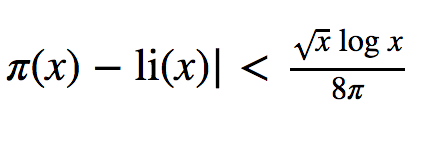
一种可以用来估计素数数量的方法是 Riemann R 函数。这是 π(x) 的一个平滑近似。该函数使用快速收敛的 Gram 级数定义:
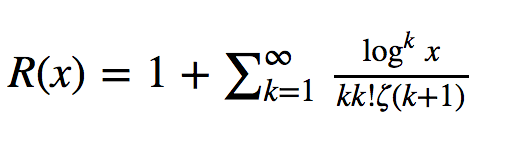
一个示例运行是 [ 这里]:
Range from 0 to 1000000
Estimation of primes: 78498
Possibility of finding prime (%): 7.8498
----- Using Riemannr method to estimate
Estimation is: 78527Range Est number of primes
10^ 1 4
10^ 2 25
10^ 3 168
10^ 4 1226
10^ 5 9587
10^ 6 78527
10^ 7 664667
10^ 8 5761551
10^ 9 50847455
10^ 10 455050683
10^ 11 4118052494
10^ 12 37607910542
10^ 13 346065531065
10^ 14 3204941731601
10^ 15 29844570495886
10^ 16 279238341360977
10^ 17 2623557157055978
10^ 18 24739954284239496
10^ 19 234057667300228928
10^ 20 2220819602556027136
10^ 21 21127269485932298240
10^ 22 201467286689188773888
10^ 23 1925320391607837261824
10^ 24 18435599767347541311488
10^ 25 176846309399141946490880
10^ 26 1699246750872419937812480
10^ 27 16352460426841662628560896
10^ 28 157589269275973244548022272
10^ 29 1520698109714271704874745856
10^ 30 14692398897720432138328735744在这种情况下,如果我们随机选择一个 0 到 1,000,000 之间的数字,那么我们找到素数的概率是 7.84%。通常,当我们选择一个随机素数时,我们从一个随机数开始,然后不断地从该值中减 1,并测试它,直到找到一个素数。
因此,如果我们的攻击者每秒尝试 10 亿个素数,那么如果我们选择一个在 1⁰⁵⁰ 范围内的素数,那么尝试所有素数大约需要 29,800 秒,也就是 8 小时。因此,我们需要确保素数大小足够大,以便入侵者有太多的素数要查找才能破解密钥。
如果你有兴趣,1⁰³⁰ 相当于 99 位。通常,对于 RSA,我们使用 2,048 位,因此入侵者必须搜索大量的素数。这是我的一个小小的 Python 代码,可以将 1⁰³⁰ 转换为位:
>>> import math
>>> y=10**30
>>> print math.log10(y)/math.log10(2)
99.6578428466寻找跳跃
在生成给定比特大小的随机素数时,我们只需以数字方式(以及给定的比特数)生成一个随机数。然后我们把它变成一个奇数,然后可以使用 Miller-Rabin 方法来确定它是否是素数。如果不是,我们增加 2,然后再测试。我们将继续,直到找到一个素数。因此,如果找到素数的概率是 10%,我们有 1/5 的机会找到素数,因此我们很可能平均需要递增 5 次才能找到素数。
然后,我们可以生成一个随机奇数,然后测试它的素性,如果它不是素数,我们可以增加 2,然后重新测试,直到我们找到一个素数 [这里]:
"== Random Prime with Miller-Rabin Test == "
$randBytes=16
$randBytes = [int]$Args[0]
$val=GetRandomBigInteger($randBytes)
if ($val -le 0) { $val=-$val}
if (($val % 2) -eq 0) { $val=$val+1}
"Random prime size: "+$randBytes+ " Bytes, Bits: "+$randBytes*8
"`nStarting value:`t"+$val$flag=$False
$jumps=0for ($i=0;$i -le 2000; $i=$i+1) {
$is_prime = isItPrime $val 4
if ($is_prime -eq $True) {
$flag=$True
$jumps=2*$i
break
}
$val=$val+2}if ($flag -eq $True) {"Random prime:`t"+$val
"Jump to find:`t"+$jumps如果你有兴趣,这里有一些数学方法可以确定在给定范围内找到素数的概率:
https://asecuritysite.com/primes/nprime
作为一个例子,我已经用 PowerShell 编写了代码[ 这里]:
function GetRandomBigInteger($size) {
$rand = [Security.Cryptography.RandomNumberGenerator]::Create()
$r = [byte[]]::new($randBytes)
$rand.GetBytes($r)
$val = [Numerics.BigInteger]::new($r)
return ($val)
}
function PrimeRabinMiller($d, $n) {
$a = GetRandomBigInteger 2 ($n - 1)
$x= [System.Numerics.BigInteger]::ModPow($a, $d, $n);
If (($x -eq 1) -or ($x -eq ($n - 1))) {
return $True
}
While ($d -ne ($n-1)) {
$x = ($x * $x) % $n;
$d = $d*2
if ($x -eq 1) { return $False }
if ($x -eq ($n-1)) {
return $True
}
}
return $False
}
function isItPrime($n, $k) {
if ($n -eq 2 -or $n -eq 3 -or $n -eq 5 ) { return $True }
$d = $n - 1;
while (($d % 2) -eq 0) {
$d = $d/2;
}
for ($i = 0; $i -lt $k; $i=$i+1) {
$rtn=PrimeRabinMiller $d $n
if ($rtn -eq $False) {
return $False;
}
}
return $True;
}
"== Random Prime with Miller-Rabin Test == "
$randBytes=16
$randBytes = [int]$Args[0]
$val=GetRandomBigInteger($randBytes)
if ($val -le 0) { $val=-$val}
if (($val % 2) -eq 0) { $val=$val+1}
"Random prime size: "+$randBytes+ " Bytes, Bits: "+$randBytes*8
"`nStarting value:`t"+$val
$flag=$False
$jumps=0
for ($i=0;$i -le 2000; $i=$i+1) {
$is_prime = isItPrime $val 4
if ($is_prime -eq $True) {
$flag=$True
$jumps=2*$i
break
}
$val=$val+2
}
if ($flag -eq $True) {
"Random prime:`t"+$val
"Jump to find:`t"+$jumps
}一个示例运行是 [ 这里]:
== Random Prime with Miller-Rabin Test ==
Random prime size: 128 Bytes, Bits: 1024Starting value: 74694127609839394531423695066683807367213906691835690628010806941823113116341160452233302154382226520304305016921580485423591227892665244629327378091261259183162478412317239748423133148888508256284739076437146819181993895696424719945351704588366388739351351476790041575981862249517999445249166915727466313195
Random prime: 74694127609839394531423695066683807367213906691835690628010806941823113116341160452233302154382226520304305016921580485423591227892665244629327378091261259183162478412317239748423133148888508256284739076437146819181993895696424719945351704588366388739351351476790041575981862249517999445249166915727466314951
Jump to find: 1756对于一个 512 位的素数:
== Random Prime with Miller-Rabin Test ==
Random prime size: 64 Bytes, Bits: 512Starting value: 1570047489143950971158469706647749642676906610685433069032127727599272773500362380171988197033189544118765224161943698783713549815590440492717110990773387
Random prime: 1570047489143950971158469706647749642676906610685433069032127727599272773500362380171988197033189544118765224161943698783713549815590440492717110990773583
Jump to find: 196对于一个 256 位的素数:
== Random Prime with Miller-Rabin Test ==
Random prime size: 32 Bytes, Bits: 256Starting value: 678561933854231032073566346504160285991810520328758260539775958564099341129
Random prime: 678561933854231032073566346504160285991810520328758260539775958564099341417
Jump to find: 288跳跃值与从随机数开始查找素数有关。在上面的例子中,我们递增 288 以从我们的起点找到下一个素数。一般来说,素数越小,跳跃次数就越少。因此,大数通常需要更长的时间才能生成,因为可能会进行更多的测试。
结论
为了你的在线安全,随机数很重要。如果这些数字在某种程度上不是随机的,你的安全可能会受到损害。但是,素数的空间越大,我们就必须搜索越多,这就是生成大素数在 CPU 时间方面成本高昂的原因,但对于你的安全却如此重要。因此,对于 2K RSA,我们生成 1K 素数,这些素数应该是随机的。
- 原文链接: medium.com/asecuritysite...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 翻译
- 学分: 6
- 分类: 密码学
- 标签: 质数 RSA 密码学 Miller-Rabin测试 Riemann R函数 Sieve of Eratosthenes
- 以太坊协议研究学习小组 - 2026 启动 86 浏览
- 神奇的 Zig、C 和 OpenSSL 132 浏览
- Shamir份额的魔力:BLS门限签名 388 浏览
- zkMesh:2026年1月回顾 396 浏览
- FRI (and friends) 使用 Lean4 形式化验证 FRI(及相关内容) 393 浏览
- ZK 编年史:电路(第二部分) 396 浏览
- 有限域之美与力量 (以及 Zig) 491 浏览
- 扳手攻击:发生与预防 524 浏览
- zkEVM 安全性概览 588 浏览
- 基于哈希函数的签名(三):多次签名 668 浏览
- 基于哈希函数的签名(二):少量次数签名 836 浏览
- Zig 签名(Ed25519 和 ECDSA) 1174 浏览

