当密文等于消息时：RSA中的消息隐藏

当密码等于消息：RSA 中的消息隐藏

想象一下，你创建了一个密码，有时当你加密时，密码实际上就是原始消息。例如，当你进行字母移位，并将字母移动 26 个位置时，最终会得到“a”到“A”，“b”到“B”等等的映射，这种情况就可能发生。

现场演示

我喜欢在密码学中进行现场演示，并且尽可能用观众选择的参数来演示关键原理。我最喜欢的两个是 Diffie-Hellman 方法和 RSA 公钥加密方法 —— 而且我知道无论观众选择什么，我总是能得到正确的结果。大多数时候，这些方法都非常有效，而且我可以揭示正确的答案。但是，有时，我最终得到的密码与消息相同 —— 显然，这不是很安全！所以，昨天在去伦敦的路上，我设法在我的 iPad 上运行了 Python，并且能够确定我应该避免的值，以及对于给定的 RSA 方法中的素数集合，我找到一个非隐藏值的概率。

RSA 方法

我们首先生成两个素数（p，q），然后计算模数（N）：

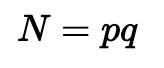
这个模数（N）是 RSA 安全性的核心，并且必须难以确定给定模数值的素数。因此，我们的素数必须具有难以分解的大小，并且必须是随机生成的。接下来，我们计算 ϕ(N)，它是：

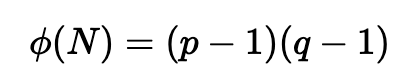
然后我们选择 e，使其不与 ϕ(N) 共享一个因子：

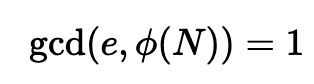
其中 gcd 是最大公约数。在实践中，e 通常具有 65,537 的值（这是一个素数，所以是安全的）。加密密钥现在是 (e,N)。Bob 然后将其发送给 Alice，让她使用此公钥加密消息。我们用以下公式确定解密值 (d)：

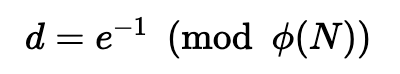
为此，我们使用逆模函数来确定 d。在下面的代码中，我们使用：

d=pow(e,-1,PHI)

要加密消息 (M)，我们使用：

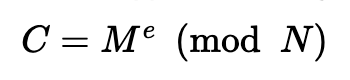
解密：

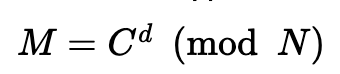
消息隐藏

对于 RSA，将存在一些消息值映射到相同的密文，并且消息将不会被隐藏。例如，如果我们有一个整数消息 13，那么在我们应用公共指数 (e) 和模数值 (n) 之后，加密消息也可能是 13。在下面，我们可以使用小素数来揭示不会被隐藏的值 [ 这里]：

import math
import sys

p=13
q=7
e=3

if (len(sys.argv)>1):
        p=int(sys.argv[1])
if (len(sys.argv)>2):
        q=int(sys.argv[2])
n=p*q
PHI=(p-1)*(q-1)
while (math.gcd(e,PHI)!=1):
 e=e+2
d=pow(e,-1,PHI)
print(f"e={e}, d={d}, n={n}, p={p}, q={q}, PHI={PHI}")
for m in range(0,n):
 c=pow(m,e,n)
 if (c==m): print(f"{m} {c}")

unconceal=(1+math.gcd(e-1,p-1))*(1+math.gcd(e-1,q-1))

print(f"Unconcealed = {unconceal}")
print(f"Percentage = {round(unconceal/n*100,1)}%")

使用 11 和 31 的素数，我们得到 [ 这里]：

e=7, d=43, n=341, p=11, q=31, PHI=300
e=7, d=43, n=341, p=11, q=31, PHI=300
0 0
1 1
32 32
56 56
67 67
87 87
88 88
98 98
99 99
154 154
155 155
186 186
187 187
242 242
243 243
253 253
254 254
274 274
285 285
309 309
340 340
Unconcealed = 21
Percentage = 6.2%

其中有 21 条消息将创建与明文值相同的密文。这包括 M =340 和 M =154。我们实际上可以计算未隐藏值的数量为：

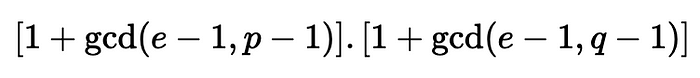
在现实生活中，我们将有一个 e 为 65,537 和一个 1,024 位的素数。如果我们尝试一个相当小的素数 2^{255}-19，我们只会得到 25 个未隐藏的值：

>>> import math
>>> e=65537
>>> p=2**255-19
>>> q=2**255-19
>>> unconceal=(1+math.gcd(e-1,p-1))*(1+math.gcd(e-1,q-1))
>>> print (unconceal)
25

你可以在这里尝试一些例子：

https://asecuritysite.com/rsa/rsa_conceal

• 原文链接： medium.com/asecuritysite...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～