惠普发布量子安全打印机

HP发布了首款量子安全的打印机，使用了基于哈希的数字签名方法，如LMS和W-OTS。LMS使用Winternitz一次性签名方案，并利用Merkle树来验证私钥。文章还提供了使用Bouncy Castle库在C中实现LMS的示例代码，并展示了不同参数设置下的密钥和签名长度。

惠普发布量子安全的打印机

所以，准备好迎接支持“量子安全”标签的设备，将其作为一种营销工具吧。最近，三星发布了带有后量子密码芯片的新款 S25 智能手机，现在惠普发布了一款支持后量子数字签名的打印机 [ here]:

不管你喜不喜欢，由于量子计算机的进步，我们很可能要告别所有现有的公钥方法，包括 ECDH 和 RSA（用于密钥交换）以及 RSA、ECDSA、EdDSA 和 ElGamal（用于数字签名）。替代方案是什么？嗯，一种替代数字签名的方法是使用基于哈希的方法，我们创建大量的私钥，然后将这些私钥哈希到 Merkle 根。然后，根哈希是验证我们所有私钥的公钥。在 NIST 的 PQC（Post Quantum Cryptography，后量子密码学）竞赛中，SPHINCS+ 方法获得批准，并在 FIPS 205 标准中定义，与 Dilithium (ML-DSA — FIPS 204) 和 Falcon 一起。总的来说，该方法使用 Winternitz 一次性签名方案 (W-OTS)，并提供相对较小的私钥和公钥以及相当小的密文大小。

IETF 和 NIST 提出的支持 PQC 数字签名的方法是 LMS ( Leighton-Micali Hash-Based Signature，Leighton-Micali 基于哈希的签名) [1]，并在 RFC 8554 中定义 [ here]:

与 SPHINCS+ 一样，LMS 使用 WOTS 一次性签名方案。那么让我们实现 LMS 方法。

总的来说，我们生成许多私钥并将它们哈希成 Merkle 树，根哈希就是与所有这些私钥关联的公钥。如果根公钥的节点编号为 1，那么它的子节点的节点编号将为 2 和 3。如果我们定义我们有一个 h 层并且位于节点 N，那么左子节点将是 2*N，右节点将是 2*N+1。因此，每一层将有叶子节点 2^h,(2^h)+1, (2^h)+2, …, (2^h)+(2^h)-1:

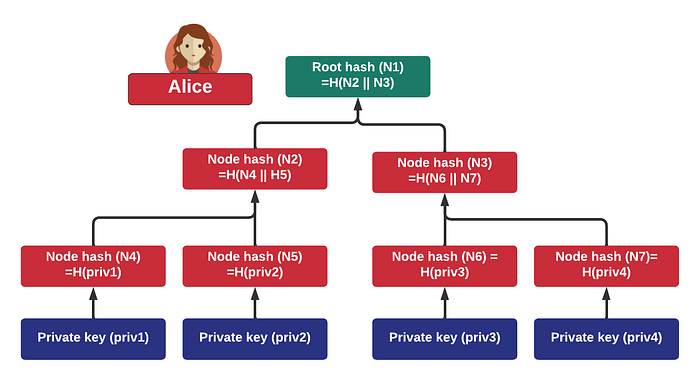
Winternitz 一次性签名方案 (W-OTS)

W-OTS 方法由斯坦福大学数学系的 Robert Winternitz 提出。它使用相对较小的密钥和签名大小，并且被认为是量子安全的。总的来说，它生成 32×256 位的随机私钥。然后我们将这些私钥哈希多次，由参数 (w) 定义。如果我们使用 w=8，我们哈希 (2w) 次私钥。这将创建 32×256 位的公钥。通过一次取八位来创建签名，然后从 256 中减去 8 位二进制整数 (n)，并且私钥被哈希 256-n 次。然后，签名是由随机私钥派生的 32 个哈希值。为了验证签名，接收者解析签名哈希（一次使用 8 位并提取 8 位整数 n）。然后，签名从签名中导出。

该方法是：

  • 最初，我们创建 32 个 256 位随机数。这 32 个值将是我们的私钥。
  • 然后，我们将每个值哈希 256 次。这 32 个值将是我们的公钥。
  • 现在我们获取消息并使用 SHA-256 对其进行哈希处理。这将生成 32 个 8 位值（N1、N2 … N32）。
  • 对于签名。我们获取消息哈希中的每个 8 位值，然后哈希 256-N 次（其中 N 是 8 位值的值）。
  • 为了证明签名，我们获取消息并使用 SHA-256 对其进行哈希处理，然后获取每个 8 位值。然后，我们将 8 位签名值哈希消息哈希值定义的次数（N1、N2..）。每次操作的结果应等于公钥值。

如下图所示：

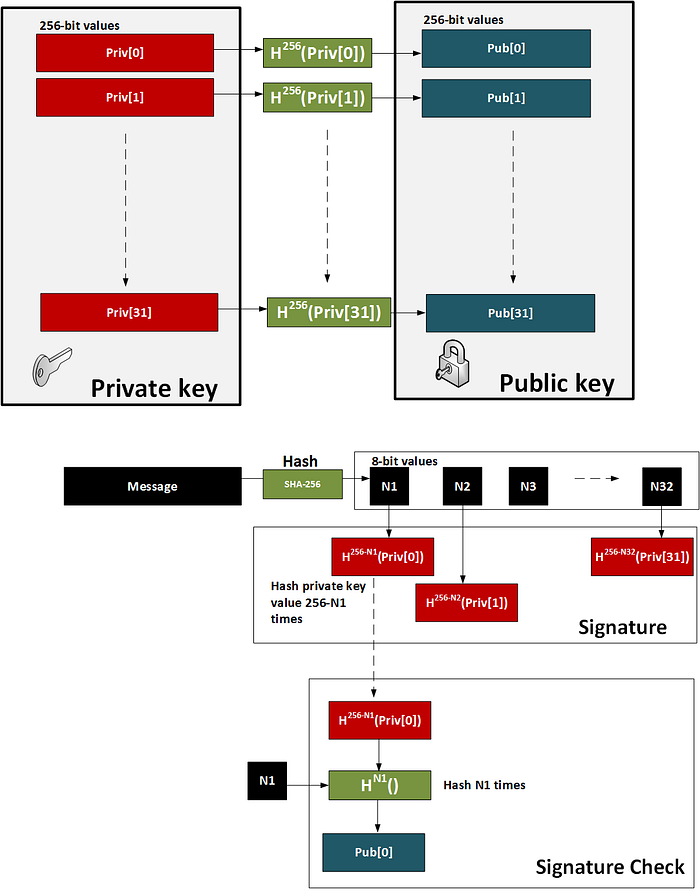
一个示例运行，显示了前几个私钥和第一个公钥 [ here]：

Hashing number: 256
==== Private key (keep secret) =====
Priv[0]:  bd344c6110628aa38c9b5ca6458bed7b78425b2e82efa0624a578031562f82ee
Priv[1]:  20670af5b1663fa9fad49fab6a692ae5989cff77439f98d2288f173b17a8d99f
Priv[2]:  625aa290fd1f88c930451ff743d5d9ef90e7064368fb23a18c9fd048474818f2
Priv[3]:  ee0e1363cbd5f61017ba27bfe91ec53969d28d143ed59a99efb020941bc4990f
Priv[4]:  ce94d7282ee3f7b05b99768695ff224b5994900c6182dfb89d596d8b7b405ec6
Priv[5]:  d0c59651e951b0bb8d5a2d7b93f6739c9ce4a0c0c0f63bfce23b331b947eb285
==== Public key (show everyone)=====
Pub[0]:  45fdac6339e80cadd1331cce026cd0364ea84146a36f6f3f2449b66fb55a217a
Pub[1]:  184cf92f22072fef078fa4a93ec2044f07ac8b12e326509474209312cace8a5a
Pub[2]:  a47548d4537bd284e7d7f935f41570866d9c6a72c463bb2a2b10c8c7907621f0
Pub[3]:  60395e575522cacb70d866211c64e8a74e562c79d1fffce224d1013d088bf66f
Pub[4]:  8be7b53d5b56e698b8798f2a707fba7b8e417554fd489d74cc40fe8574d7589e
Pub[5]:  9fac35971dae3a5c77ae7b5c720a72f90ee53852668c96c78e095cbb52af20a1
==== Message to sign ===============
Message:    The quick brown fox jumps over the lazy dog
SHA-256:    d7a8fbb307d7809469ca9abcb0082e4f8d5651e46d3cdb762d02d0bf37c9e592
==== Signature =====================
Sign[0]:    45cb53c5c33af9b20426fd0233fd63d92bf0c2ded367163e6f2f93588a33c6d8
Sign[1]:    e8c35987101f2d11d7056a2fe78069d3ed73aee315ebef8c2d40e04973301c26
Sign[2]:    59220d80b7c958957b28511f4081341cc4a00a0d6d5e1d05351be7dec3ca8aaa
Sign[3]:    72a906d719be18e1592314bf6f6c521a325a9de2b5b9e9e13117bf01b0157f5c
The signature test is  True

该方法的演示在此处给出 here。

LMS

在 WOTS 实现中，我们有许多参数，这些参数会改变我们实现的安全级别：

|------------------------------------------------------------|
  | Parameter Set Name  | H      | n  | w | p   | ls | sig_len |
  |------------------------------------------------------------|
  | LMOTS_SHA256_N32_W1 | SHA256 | 32 | 1 | 265 | 7  | 8516    |
  |                     |        |    |   |     |    |         |
  | LMOTS_SHA256_N32_W2 | SHA256 | 32 | 2 | 133 | 6  | 4292    |
  |                     |        |    |   |     |    |         |
  | LMOTS_SHA256_N32_W4 | SHA256 | 32 | 4 | 67  | 4  | 2180    |
  |                     |        |    |   |     |    |         |
  | LMOTS_SHA256_N32_W8 | SHA256 | 32 | 8 | 34  | 0  | 1124    |
  |------------------------------------------------------------|

在这种情况下，n 是哈希大小（32 字节 - 256 位），p 是 n 字节字符串元素的数量。然后我们有 n 乘以 p 个密钥可以使用，其中签名长度是 n 乘以 p + 4 + 32 字节。表中最小的签名长度是 LMOTS_SHA256_N32_W8，长度为 1,124 字节。

在 RFC 中，我们用 m 表示与每个私钥关联的字节数，h 表示 Merkle 树的高度。然后，一个 LMS 私钥被定义为 2^h 个 OTS 私钥：

+--------------------+--------+----+----+
| Name               | H      | m  | h  |
+--------------------+--------+----+----+
| LMS_SHA256_M32_H5  | SHA256 | 32 | 5  |
|                    |        |    |    |
| LMS_SHA256_M32_H10 | SHA256 | 32 | 10 |
|                    |        |    |    |
| LMS_SHA256_M32_H15 | SHA256 | 32 | 15 |
|                    |        |    |    |
| LMS_SHA256_M32_H20 | SHA256 | 32 | 20 |
|                    |        |    |    |
| LMS_SHA256_M32_H25 | SHA256 | 32 | 25 |
+--------------------+--------+----+----+

那么私钥的数量是 2^h * ((n*p)+4)。对于 LMS_SHA256_M32_H5，我们将得到 ²⁵ *((32*34) + 4) = 34 944 字节 ~ 34 KB。请注意，无需存储私钥，因为我们可以根据需要随时计算树。这导致更多的处理但更少的内存存储。与其他方法相比，密钥大小的比较是：

Method                           Public key size    Private key size   Signature size  Security level
------------------------------------------------------------------------------------------------------
LMS_sha256_n32_h5                        56                 72              2,348
LMS_sha256_n32_h10                       56                 72              2,508
LMS_sha256_n32_h15                       56                 72              2,668

RSA-2048                                256                256                256
ECC 256-bit                              64                 32                256
Crystals Dilithium 2 (Lattice)        1,312              2,528              2,420         1 (128-bit) Lattice
Crystals Dilithium 3                  1,952              4,000              3,293         3 (192-bit) Lattice
Crystals Dilithium 5                  2,592              4,864              4,595         5 (256-bit) Lattice
Falcon 512 (Lattice)                    897              1,281                690         1 (128-bit) Lattice
Falcon 1024                           1,793              2,305              1,330         5 (256-bit) Lattice
Rainbow Level Ia (Oil-and-Vineger)  161,600            103,648                 66         1 (128-bit) UOV
Rainbow Level IIIa                  861,400            611,300                164         3 (192-bit) UOV
Rainbow Level Vc                  1,885,400          1,375,700                204         5 (256-bit) UOV
Sphincs SHA256-128f Simple               32                 64             17,088         1 (128-bit) Hash-based
Sphincs SHA256-192f Simple               48                 96             35,664         3 (192-bit) Hash-based
Sphincs SHA256-256f Simple               64                128             49,856         5 (256-bit) Hash-based
Picnic 3 Full                            49                 73             71,179         3 (192-bit) Symmetric
GeMSS 128                           352,188                 16                 33         1 (128-bit) Multivariate
GeMSS 192                         1,237,964                 24                 53         1 (128-bit) Multivariate

现在，让我们使用 Bouncy Castle 库实现 LMS [ here]：

namespace LMS
{
    using Org.BouncyCastle.Pqc.Crypto.Lms;
    using Org.BouncyCastle.Security;
    class Program
    {
        static void Main(string[] args)
        {
try {

                var msg="Hello"; // 信息
                 var method="lms_sha256_n32_h5"; // 方法
                if (args.Length >0) msg=args[0];
                if (args.Length >1) method=args[1];
                var random = new SecureRandom();
                var keyGenParameters = new LmsKeyGenerationParameters(new LmsParameters(LMSigParameters.lms_sha256_n32_h25, LMOtsParameters.sha256_n32_w4),random);
                if (method=="lms_sha256_n32_h5") keyGenParameters = new LmsKeyGenerationParameters(new LmsParameters(LMSigParameters.lms_sha256_n32_h5, LMOtsParameters.sha256_n32_w4),random);
                else if (method=="lms_sha256_n32_h10") keyGenParameters = new LmsKeyGenerationParameters(new LmsParameters(LMSigParameters.lms_sha256_n32_h10, LMOtsParameters.sha256_n32_w4),random);
     //           else if (method=="lms_sha256_n32_h15") keyGenParameters = new LmsKeyGenerationParameters(new LmsParameters(LMSigParameters.lms_sha256_n32_h15, LMOtsParameters.sha256_n32_w4),random);
     //           else if (method=="lms_sha256_n32_h20") keyGenParameters = new LmsKeyGenerationParameters(new LmsParameters(LMSigParameters.lms_sha256_n32_h20, LMOtsParameters.sha256_n32_w4),random);
      //          else if (method=="lms_sha256_n32_h25") keyGenParameters = new LmsKeyGenerationParameters(new LmsParameters(LMSigParameters.lms_sha256_n32_h25, LMOtsParameters.sha256_n32_w4),random);
                var keyPairGen = new LmsKeyPairGenerator();
                keyPairGen.Init(keyGenParameters);
                var keyPair = keyPairGen.GenerateKeyPair();
                var pubKey = (LmsPublicKeyParameters)keyPair.Public;
                var privKey = (LmsPrivateKeyParameters)keyPair.Private;
                // Signing  // 签名
                var aliceSign = new LmsSigner();
                aliceSign.Init(true, privKey);
                var signature = aliceSign.GenerateSignature(System.Text.Encoding.UTF8.GetBytes(msg));
                // verify signature  // 验证签名
                var bobVerify = new LmsSigner();
                bobVerify.Init(false, pubKey);
                var rtn = bobVerify.VerifySignature(System.Text.Encoding.UTF8.GetBytes(msg), signature);
                Console.WriteLine("Message:\t{0}",msg);
                Console.WriteLine("Method:\t\t{0}",method);
                Console.WriteLine("\nPublic key (length):\t{0} bytes",pubKey.GetEncoded().Length);
                Console.WriteLine("Alice Public key :\t{0}",Convert.ToHexString(pubKey.GetEncoded()));
                Console.WriteLine("\nPrivate key (length):\t{0} bytes",privKey.GetEncoded().Length);
                Console.WriteLine("Alice Private key:\t{0}",Convert.ToHexString(privKey.GetEncoded()));
                Console.WriteLine("\nSignature (length):\t{0} bytes",signature.Length);
                Console.WriteLine("Signature (first 50 bytes):\t\t{0}",Convert.ToHexString(signature)[..100]);
                Console.WriteLine("\nVerified:\t{0}",rtn);
            } catch (Exception e) {
                Console.WriteLine("Error: {0}",e.Message);
            }
        }
    }
}

一个使用 lms_sha256_n32_h5 的示例运行给出 [ here]：

Message:    Post Quantum Crypto
Method:     lms_sha256_n32_h5
Public key (length): 56 bytes
Alice Public key : 0000000500000003A1FC28853207AEA5B5A6B92093CF0F0B678452F69AC8F343A1A4BC3A08A14130AAF07CF46C2D4717D640B0746B8B0292
Private key (length): 72 bytes
Alice Private key: 000000000000000500000003A1FC28853207AEA5B5A6B92093CF0F0B000000010000002000000020212CF1DB290D1EFD36F43290B18C58912D251A74E5CB070DBF79B54F51B4484B
Signature (length): 2348 bytes
Signature (first 50 bytes):  00000000000000039E2822055561084B6B8567F4122C8F6970651DD985476AFA21410F5A3E4854E6F67F2479203E3B4F1BD0
Verified: True

Lms_sha256_n32_h10 [ here]:

Message:    Post Quantum Crypto
Method:     lms_sha256_n32_h10
Public key (length): 56 bytes
Alice Public key : 00000006000000036776613E88BAB931143A8657120F40BD0E909CF2D085979E22B3DF4B56D9D93D386218BA54A1AE563153A489DCCA10FD
Private key (length): 72 bytes
Alice Private key: 0000000000000006000000036776613E88BAB931143A8657120F40BD0000000100000400000000209A8104C4C968E7F9F07585F733BB1C3275268FD3C05380B5878D752469AC11DD
Signature (length): 2508 bytes
Signature (first 50 bytes):  00000000000000033E1E15A47125291359291E973C84A9A2083FEA6D67092CED1DF33AF317739D7E5ACCAD311326E63785F0
Verified: True

还有 lms_sha256_n32_h15：

Message:    Post Quantum Crypto
Method:     lms_sha256_n32_h15
Public key (length): 56 bytes
Alice Public key : 0000000700000003D4754AAC03B588E4A21723267711F2C25F9BDFA9EF7A3A07D64D580F07BFD17FFF2EDDA266248E765DF13A066CD1AEEB
Private key (length): 72 bytes
Alice Private key: 000000000000000700000003D4754AAC03B588E4A21723267711F2C2000000010000800000000020E900DC335DE013AC77B42B3523B05548A923859FCE254CD7FFF89DC62B7AD763
Signature (length): 2668 bytes
Signature (first 50 bytes):  0000000000000003C8DBA13DDDFF10554839ECA3073526564C4E59C0BCBF93EC393108EC8D6E4E336277E13A054A0C936BBF
Verified: True

参考文献

[1] McGrew, D., Curcio, M., & Fluhrer, S. (2019). RFC 8554: Leighton-Micali hash-based signatures.

  • 原文链接： billatnapier.medium.com/...
  • 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～
点赞 0
收藏 0
分享
本文参与登链社区写作激励计划 ，好文好收益，欢迎正在阅读的你也加入。

0 条评论

请先 登录 后评论
asecuritysite
asecuritysite
江湖只有他的大名，没有他的介绍。

asecuritysite

如果觉得我的文章对您有用，请随意打赏。你的支持将鼓励我继续创作！