从理论到实践--门限共享秘密算法详解

Dapplink
发布于 2025-03-31 10:55
阅读 22

本文将带领大家去理解共享秘密相关的一些技术，希望大家从中能学到一些共享密码的知识。

密码学的发展可以追溯到公元前 400 年前，人类使用密码学的历史几乎和文字的历史一样长。公元前 400 年前，斯巴达人发明了 “塞塔式密码“。在中国古代，也出现过密码学的影子的，中国古代的藏头诗大家应该都知道，这也属于密码学的使用范畴。在密码学的发展过程中，战争起到了很大的作用，从古至今，军方使用的技术都是世界上最先进的，包括密码学也一样。密码学体系在当今时代已经是一个完善的学科体系，全世界有很多专家学者终其一生为密码学的发展添砖加瓦。我们现在所熟知的对称密码，非对称密码，数字签名，单项散列函数，PKI 体系，共享密码等都可以是一个值得深入研究的方向。本文将带领大家去理解共享秘密相关的一些技术，希望大家从中能学到一些共享密码的知识。

## 一.共享密钥的发展历程

秘密的共享是信息安全研究的一个重要的分支，密码主要是为了对重要信息进行加密，保证信息的安全性，而秘密共享却可以保证密钥的安全性，它为密码学的发展提供了一个崭新的思路。秘密共享的原理是将秘密分成若干份，交给不同的人去保管，设定管理秘密的一定数量的人贡献出自己持有的秘密，就可以恢复秘密了。

### **1.1.秘密共享的产生**

秘密共享的概念最早由著名密码学家 Shamir 和 Blakley 于 1979 年分别独立提出并给出了各自的方案。Shamir 的( t，n) 门限方案基于 Lagrnage ( 拉格朗日) 插值法来实现，Blakley 的( t，n) 门限方案是利用多维空间点的性质来建立的。

秘密共享的概念一经提出，受到专家学者们的极大的关注与研究。 这些年取得的成果颇丰。大致可以分为如下几类。

#### **1.1.1.门限秘密共享方案**

在(t，n) 门限秘密共享方案中，任何包含至少 t 个参与者的集合都是授权子集，而包含 t-1 或更少参与者的集合都是非授权子集，实现( t， n) 门限秘密共享的方法除了 Shamir 和 Blakley 的方案外，还有基于中国剩余定理的 Asmuth-Bloom 法以及使用矩阵乘法的 Karnin-Greene Hellman 方法等。

#### **1.1.2.一般访问结构上秘密共享方案**

门限方案是实现门限访问结构的秘密共享方案，对于其它更广泛的访问结构存在局限性， 如在 甲 、乙 、丙 、丁 四 个成员中共享秘密，使甲和丁或乙和丙合作能恢复秘密，门限秘密共享方案就不能解决这样的情况. 针对这类问题，1987 年密码学研究人士提出了一般访问结构上的秘密共享方案。1988 年有人又提出了一个更简单有效的方法—单调电路构造法，并且证明了任何访问结构都能够通过完备的秘密共享方案加以实现。

#### **1.1.3.多重秘密共享方案**

只需保护一个子秘密就可以实现多个秘密的共享，在多重秘密共享方案中每个参与者的子秘密可以使用多次，但是一次秘密共享过程只能共享一个秘密。

#### **1.1.4.多秘密共享方案**

多重秘密共享解决了参与者的子秘密重用 的问题，但其在一次秘密共享过程中只能共享一个秘密。

#### **1.1.5.可验证秘密共享方案**

参与秘密共享的成员可以通过公开变量验证自己所拥有的子秘密的正确性，从而有效地防止了分发者与参与者，以及参与者之间的相互欺骗的问题。可验证秘密共享方案分为交互式和非交互式两种。交互式可验证的秘密共享方案是指各个参与者在验证秘密份额的正确性时需要相互之间交换信息；非交互式可验证的秘密共享是指各个参与者在验证秘密份额的正确性时不需要相互之间交换信息。在应用方面，非交互式可验证秘密共享可以减少网络通信费用，降低秘密泄漏的机会，因此应用领域也更加广泛。

####

#### **1.1.6.动态秘密共享方案**

动态秘密共享方案是 1990 年提出，它具有很好的安全性与灵活性，它允许新增或删除参与者、定期或不定期更新参与者的子秘密以及在不同的时间恢复不同的秘密等等. 以上是几种经典的秘密共享方案. 需要说明的是，一个具体的秘密共享方案往往是几个类型的集合体。

#### **1.1.7.其他秘密共享**

量子秘密共享、可视秘密共享、 基于多分辨滤波的秘密共享、基于广义自缩序列的秘密共享。

## **二.经典秘密共享方案介绍**

### **1.Shamir 门限秘密共享方案**

Shamir 门限秘密共享方案是最经典和最广泛应用的秘密共享算法之一，由著名密码学家 Adi Shamir 于 1979 年提出。

### **2.基本思想**

该方案基于 拉格朗日插值 多项式的数学原理，将一个秘密分成 n 份，分发给 n 个参与者。设定门限值 t，只有当 t 个或以上的参与者联合，才能恢复原始秘密；t−1 个或更少的参与者无法恢复任何有意义的信息。

###

### **3.数学基础：有限域 + 拉格朗日插值**

所有计算在一个素数有限域 Fp 中进行，p 是一个大素数。

使用一个 t−1 次多项式

$f(x) = a_0 + a_1x + a_2x^2 + ... + a_{t-1}x^{t-1}$，其中常数项 $a_0 = s $就是要共享的秘密。

###

### **4.算法步骤**

#### **4.1.初始化与分发阶段（由分发者 Dealer 执行）**

- 输入参数：
  - 秘密：s
  - 总参与者数：n
  - 门限值：t
  - 素数$ p >max(n,s)$

- 生成多项式：
  - 随机选择 t−1个系数 $a_1, a_2, ..., a_{t-1}∈F_p$
  - 构造多项式 $f(x) = s + a_1x + a_2x^2 + ... + a_{t-1}x^{t-1}$

- 生成份额：
  - 对每个参与者$ i∈1,2,...,n$，选定公开的 $xi≠0$
  - 计算$ y_i = f(x_i) \mod p$
  - 将份额$ (x_i, y_i $发送给参与者 $P_i$

#### **4.2.恢复阶段（参与者联合执行）**

当至少 t个参与者拿出他们的份额$ (x_1, y_1), ..., (x_t, y_t)$：使用 拉格朗日插值 恢复出多项式 f(x) 的常数项，即：

$s = f(0) = \sum_{j=1}^{t} y_j \cdot \lambda_j \mod p$

其中 λj 是拉格朗日系数：

$$
\lambda_j = \prod_{\substack{1 \leq m \leq t \\ m \neq j}} \frac{x_m}{x_m - x_j} \mod p
$$

#### **4.3.示例**

设秘密 s=1234，门限 t=3，参与者总数 n=5，素数 p=2089

- 构造多项式：f(x) = 1234 + 166x + 94x^2
- 分发份额：
  - $x_1=1 \Rightarrow y_1=f(1)=1494$
  - $x_2=2 \Rightarrow y_2=f(2)=1910$
  - $x_3=3 \Rightarrow y_3=f(3)=1607$
  - $x_4=4 \Rightarrow y_4=f(4)=986$
  - $x_5=5 \Rightarrow y_5=f(5)=47$

- 任取任意 3 个份额（如前 3 个）可以恢复出$ f(0)=1234$

#### **4.4.Shamir 共享秘密算法的优缺点**

- 优点
  - 信息论安全：任意 t−1 个或更少份额无法获取任何关于秘密的信息
  - 灵活性高：可动态添加新参与者，只需用原多项式计算新份额。
  - 支持扩展：可结合可验证机制、防篡改机制使用。

- 缺点
  - 分发者必须完全可信（否则可以恶意发送错误份额）
  - 重构阶段需要精确计算，防止恶意参与者提交无效份额
  - 每个参与者必须通过安全通道接收自己的子密钥

### **5.基于中国剩余定理的门限共享秘密算法**

中国剩余定理秘密共享方案（CRT-SSS）由 Asmuth 和 Bloom 于 1983 年提出，是一种基于模运算的秘密共享方案。该方案通过将秘密嵌入一个模数系统中，再利用中国剩余定理进行重构，具有良好的计算效率和信息论安全性。

#### **5.1.中国剩余定理简介（CRT）**

中国剩余定理描述的是：设 m_1, m_2, ..., m_n 是两两互素的整数，对于任意整数序列 a_1, a_2, ..., a_n，存在唯一整数 x 使得：

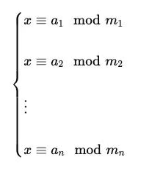
![image.png](https://img.learnblockchain.cn/attachments/2025/04/q9a2qhYw680d88c035027.png)

并且该 x 在模 $M = m_1 \cdot m_2 \cdots m_n $意义下是唯一的

#### **5.2.CRT-SSS 算法流程**

- 初始化阶段,设定以下参数：
  -  s：秘密，$0 \leq s < p$
  - p：大素数，$p > s$
  - $d_1 < d_2 < \dots < d_n$：n 个两两互素的正整数（作为模数）
  -  t：门限值
  - 满足条件：$d_1 d_2 \cdots d_t > p \cdot d_{n - t + 2} \cdots d_n$
  - 该条件保证任意 t 个份额可恢复出唯一解，而少于 t 个则不够信息恢复。

- 密钥分发阶段（由分发者执行）
  - 选择一个随机整数 $r \in [0, \left\lfloor \frac{N}{p} \right\rfloor - 1]$，其中 $$N = d_1 \cdots d_t$$
  - 计算：$s' = s + rp$
  - 对每个参与者 $P_i$，计算其份额：$x_i = s' \bmod d_i, \quad \text{for } i = 1, 2, \dots, n$
  - 将$ (x_i, d_i) $分发给参与者 P_i，其中 d_i 是公开的。

- 秘密重构阶段（由至少 t 个参与者协同完成）
  - 给定 t 个份额 $(x_{i_1}, d_{i_1}), ..., (x_{i_t}, d_{i_t})$，利用中国剩余定理计算 $$s'$$：

$$
\begin{cases}

s' \equiv x_{i_1} \pmod{d_{i_1}} \\\\

s' \equiv x_{i_2} \pmod{d_{i_2}} \\\\

\vdots \\\\

s' \equiv x_{i_t} \pmod{d_{i_t}}

\end{cases}
$$

- 恢复出 s' 后，再恢复出秘密：$s = s' \bmod p$

#### **5.3.案例分析**

设：

- 秘密 s=9，门限 t=3，总份额数 n=5
- 选素数 p=17
- 选择模数：$$d_1 = 5, d_2 = 7, d_3 = 9, d_4 = 11, d_5 = 13$$
- 选随机数 r=2

则：

$s′=9+2⋅17=43￥

- 各份额：
  - $x1=43mod5=3$
  - $x2=43mod7=1$
  - $x3=43mod9=7$
  - $x4=43mod11=10$
  - $x5=43mod13=4$

- 任取任意三个份额（如 x1,x2,x3），通过 CRT 可恢复出 $s′=43$，再恢复出 $s=43mod17=9$

#### **5.4.优缺点分析**

- 优点
  - 重构效率高，不涉及多项式插值，只用整数模运算安全性强，信息论安全，少于 t 个无法推断
  - 抗恶意修改性强，与验证机制结合后可防篡改

- 缺点
  - 参数设计复杂，模数需满足严格约束条件
  - 拓展性较差，不能轻易添加新参与者

## **三.门限共享秘密算法实际案例**

### **1.直接使用门限共享秘密算法做一个秘密拆分和恢复**

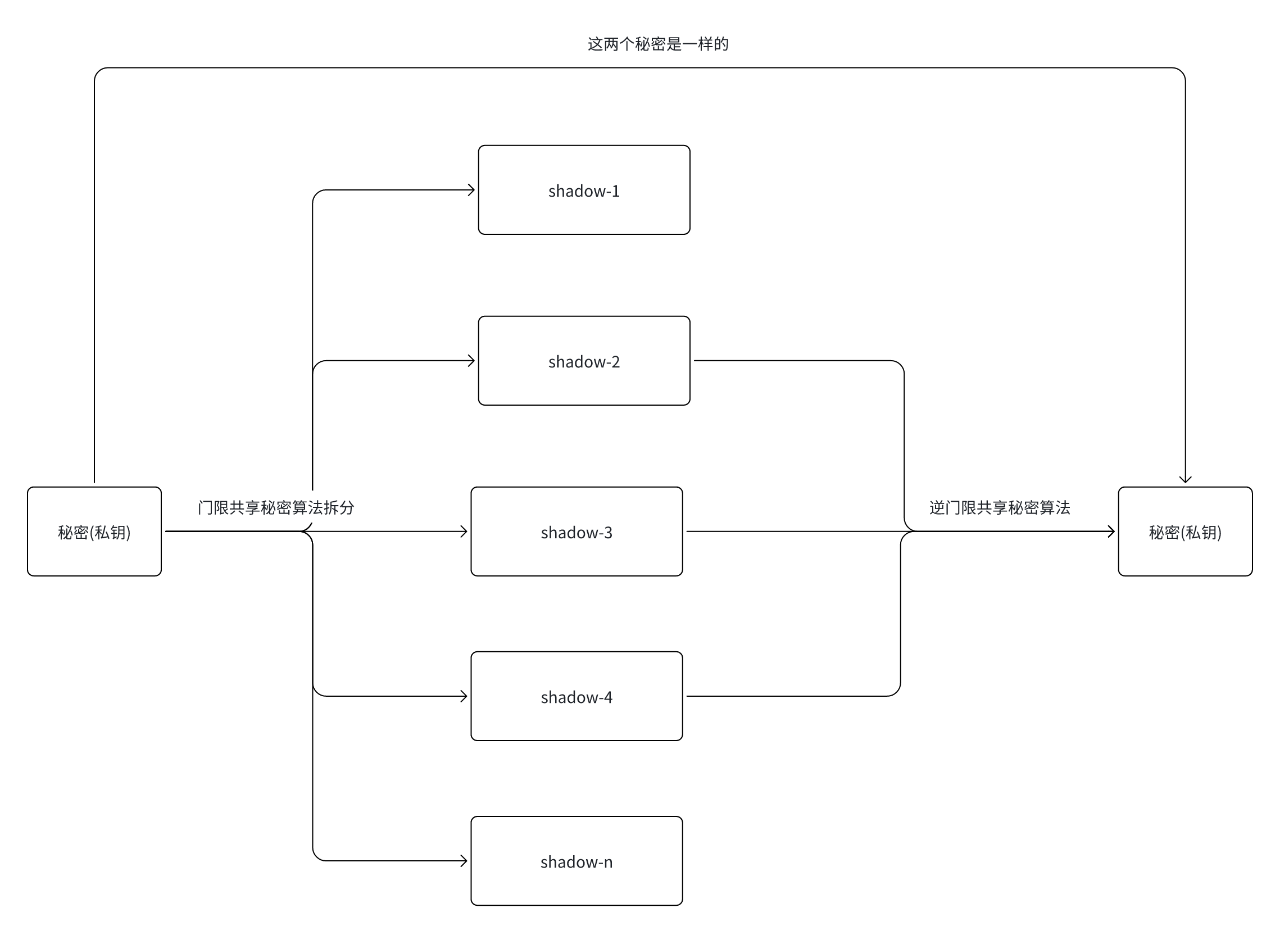
在 n 份 shadow 可以设置 k 恢复出完整的秘密(n >=k), k 就是门限值，下图将秘密拆分成 5 个 shadow, 设置 3 个可以恢复出秘密，任意选择 5 任意 3 做逆门限共享秘密算法可以恢复出完整的秘密(私钥)。

![6f718808ea8103058325aa169d6c4a58.png](https://img.learnblockchain.cn/attachments/2025/04/L2E17frQ680d8935cae34.png)

- 初始状态：私密信息（例如：私钥）
- 秘密拆分：
  - 使用门限秘密共享算法（如 Shamir Secret Sharing）
  - 将私密信息拆分成 n 份，分别称为 shadow-1、shadow-2、...、shadow-n
  - 说明：拆分的参数为 (t, n)，意思是总共 n 份，只需要任意 t 份即可还原出原始秘密。

- 秘密分发：将这些 shadow 分别交给不同的参与者/节点保管
- 秘密还原：
  - 收集任意 t 个 shadow（图中为 shadow-2、shadow-3，shadow-4）
  - 通过 逆门限秘密共享算法进行计算，成功还原出原始秘密（私钥）

- 还原后的私钥与原始私钥完全一致（图中注释：“这两个秘密是一样的”）

### **2.云端可干扰的抗秘密丢失的解决方案**

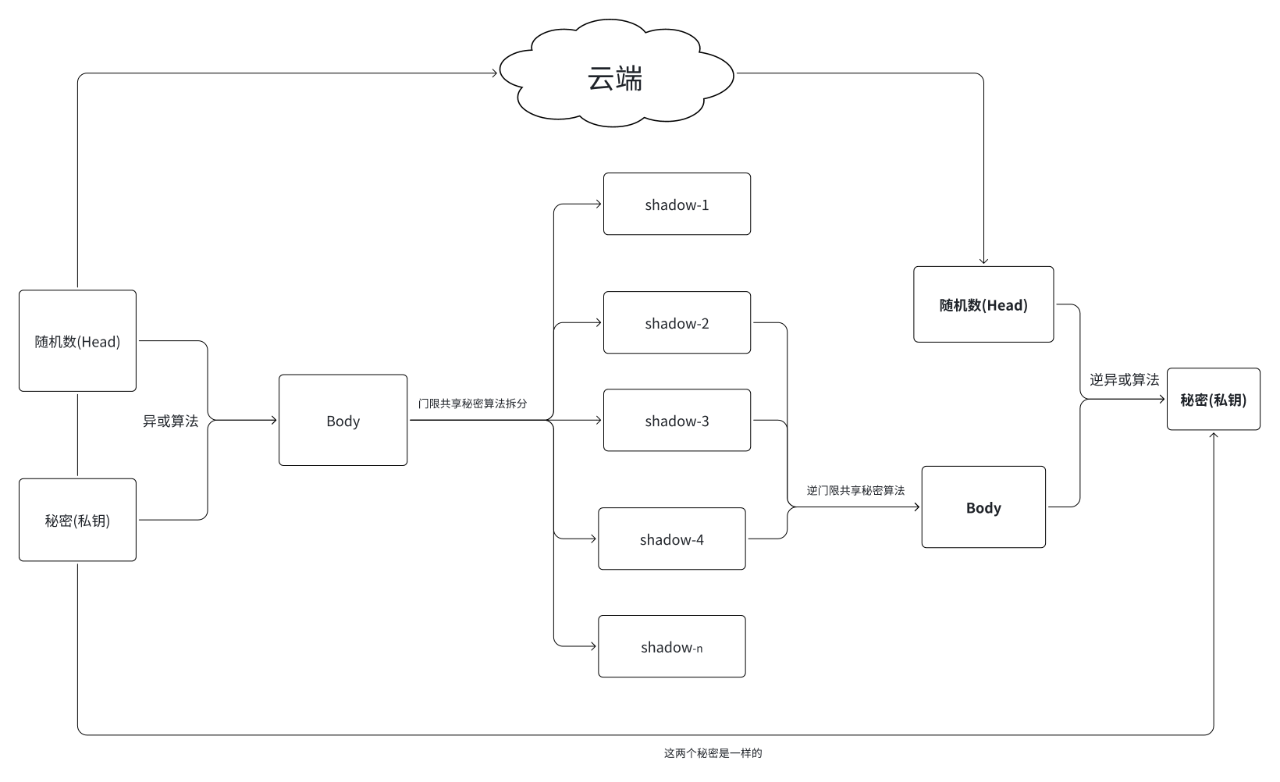
![814bd493fce6095b1e15d6780a51691d.png](https://img.learnblockchain.cn/attachments/2025/04/aKiiWIDj680d893e13e12.png)

#### **2.1.分片流程**

- 原始数据输入：原始私钥（秘密）
- 随机数（Head） ← 随机生成
- 异或计算：使用异或算法对“私钥”和“随机数（Head）”进行计算得到 Body
- Head 上传云端：将 Head 上传到云端
- 分片阶段：
  - 使用门限秘密共享算法（如 Shamir）对 Body 进行拆分
  - 拆分成多个 shadow 份额，如：shadow-1、shadow-2、...、shadow-n

- shadow 分发阶段：

- 将所有 shadow 分发给不同的人或者平台存储

#### **2.2.还原流程**

- 数据拉取
  - 从云端获取 Head
  - 从不同的人或者平台拿到 t 份 shadow

- 恢复 Body：使用逆门限秘密共享算法组合 t 个 shadow 还原出加密体 Body
- 逆异或算法：使用逆异或算法，通过 Body 和 Head 恢复出原始私钥
- 最终输出：成功恢复出与初始完全一致的私钥

###

### **3.代码**

- java 版本： https://github.com/dapplink-labs/beeKey_java
- nodeJs 版本：https://github.com/dapplink-labs/dapplink-secret

## **三.本节小结**

本节深入讲解了门限共享秘密算法的发展历程、核心原理与两种经典实现方式，并结合实际场景与可视化流程图，帮助读者全面理解如何利用该类算法保障私钥等敏感数据的安全性。

我们首先回顾了密码学的发展历史，从古代的塞塔式密码到现代复杂的公钥体系，再到今天的共享秘密算法，密码学始终围绕着“信息安全”这一核心目标演进。其中，“秘密共享”技术为密钥的安全管理提供了全新的解决方案：即通过“将一个秘密分成多份，设定门限值 t，只要收集到 t 份或以上，就可以还原出原始秘密”的方式，构建出具有高度鲁棒性和灵活性的密钥保护机制。

在秘密共享的发展历程中，最经典的就是由 Shamir 提出的 (t, n) 门限秘密共享方案，它基于拉格朗日插值法，通过构造一个 t-1 次多项式将秘密编码进常数项，并生成 n 个点分发给不同的参与者。只要收集 t 个或以上的点，就可以通过插值法恢复出原始多项式及其常数项，即秘密本身。该方法具备信息论安全性：少于 t 个份额无法获取任何关于原始秘密的信息。

本节还介绍了另一种经典方案 —— 基于中国剩余定理（CRT）的秘密共享方案，它通过整数模运算实现秘密嵌入和恢复，避免了多项式插值计算，重构效率更高，在某些场景下具备更好的性能优势。

在实际应用方面，我们展示了两种典型案例：

基础版本：私钥的 Shamir 分片与恢复 —— 使用 (t, n) 分片技术拆分私钥，确保在多方参与者中，即使部分节点离线或丢失数据，仍可安全恢复；

进阶版本：引入随机数 Head 的抗篡改设计 —— 使用随机数与私钥异或加密得到 Body，并将 Head 与 Body 分开存储（如 Body 被分片存储于多方，Head 存于云端），即便某一方数据泄露，也难以重构出原始秘密，从而进一步增强了安全性和抗攻击能力。

本节还简要提及了多个扩展方案，例如支持动态参与者变更的动态秘密共享方案、一次共享多个秘密的多秘密共享与多重秘密共享方案，以及具备验证能力的可验证秘密共享（VSS）等。这些方案分别从不同维度扩展了秘密共享算法的适用场景与安全边界。

一.共享密钥的发展历程

1.1.秘密共享的产生

秘密共享的概念一经提出，受到专家学者们的极大的关注与研究。这些年取得的成果颇丰。大致可以分为如下几类。

1.1.1.门限秘密共享方案

1.1.2.一般访问结构上秘密共享方案

门限方案是实现门限访问结构的秘密共享方案，对于其它更广泛的访问结构存在局限性，如在甲、乙、丙、丁四个成员中共享秘密，使甲和丁或乙和丙合作能恢复秘密，门限秘密共享方案就不能解决这样的情况. 针对这类问题，1987 年密码学研究人士提出了一般访问结构上的秘密共享方案。1988 年有人又提出了一个更简单有效的方法—单调电路构造法，并且证明了任何访问结构都能够通过完备的秘密共享方案加以实现。

1.1.3.多重秘密共享方案

1.1.4.多秘密共享方案

多重秘密共享解决了参与者的子秘密重用的问题，但其在一次秘密共享过程中只能共享一个秘密。

1.1.5.可验证秘密共享方案

1.1.6.动态秘密共享方案

1.1.7.其他秘密共享

量子秘密共享、可视秘密共享、基于多分辨滤波的秘密共享、基于广义自缩序列的秘密共享。

二.经典秘密共享方案介绍

1.Shamir 门限秘密共享方案

Shamir 门限秘密共享方案是最经典和最广泛应用的秘密共享算法之一，由著名密码学家 Adi Shamir 于 1979 年提出。

2.基本思想

该方案基于拉格朗日插值多项式的数学原理，将一个秘密分成 n 份，分发给 n 个参与者。设定门限值 t，只有当 t 个或以上的参与者联合，才能恢复原始秘密；t−1 个或更少的参与者无法恢复任何有意义的信息。

3.数学基础：有限域 + 拉格朗日插值

所有计算在一个素数有限域 Fp 中进行，p 是一个大素数。

使用一个 t−1 次多项式

$f(x) = a_0 + a_1x + a2x^2 + ... + a{t-1}x^{t-1}$，其中常数项 $a_0 = s $就是要共享的秘密。

4.算法步骤

4.1.初始化与分发阶段（由分发者 Dealer 执行）

输入参数：
- 秘密：s
- 总参与者数：n
- 门限值：t
- 素数$ p >max(n,s)$
生成多项式：
- 随机选择 t−1个系数 $a_1, a2, ..., a{t-1}∈F_p$
- 构造多项式 $f(x) = s + a_1x + a2x^2 + ... + a{t-1}x^{t-1}$
生成份额：
- 对每个参与者$ i∈1,2,...,n$，选定公开的 $xi≠0$
- 计算$ y_i = f(x_i) \mod p$
- 将份额$ (x_i, y_i $发送给参与者 $P_i$

4.2.恢复阶段（参与者联合执行）

当至少 t个参与者拿出他们的份额$ (x_1, y_1), ..., (x_t, y_t)$：使用拉格朗日插值恢复出多项式 f(x) 的常数项，即：

$s = f(0) = \sum_{j=1}^{t} y_j \cdot \lambda_j \mod p$

其中 λj 是拉格朗日系数：

$$ \lambdaj = \prod{\substack{1 \leq m \leq t \ m \neq j}} \frac{x_m}{x_m - x_j} \mod p $$

4.3.示例

设秘密 s=1234，门限 t=3，参与者总数 n=5，素数 p=2089

构造多项式：f(x) = 1234 + 166x + 94x^2
分发份额：
- $x_1=1 \Rightarrow y_1=f(1)=1494$
- $x_2=2 \Rightarrow y_2=f(2)=1910$
- $x_3=3 \Rightarrow y_3=f(3)=1607$
- $x_4=4 \Rightarrow y_4=f(4)=986$
- $x_5=5 \Rightarrow y_5=f(5)=47$
任取任意 3 个份额（如前 3 个）可以恢复出$ f(0)=1234$

4.4.Shamir 共享秘密算法的优缺点

优点
- 信息论安全：任意 t−1 个或更少份额无法获取任何关于秘密的信息
- 灵活性高：可动态添加新参与者，只需用原多项式计算新份额。
- 支持扩展：可结合可验证机制、防篡改机制使用。
缺点
- 分发者必须完全可信（否则可以恶意发送错误份额）
- 重构阶段需要精确计算，防止恶意参与者提交无效份额
- 每个参与者必须通过安全通道接收自己的子密钥

5.基于中国剩余定理的门限共享秘密算法

5.1.中国剩余定理简介（CRT）

中国剩余定理描述的是：设 m_1, m_2, ..., m_n 是两两互素的整数，对于任意整数序列 a_1, a_2, ..., a_n，存在唯一整数 x 使得：

并且该 x 在模 $M = m_1 \cdot m_2 \cdots m_n $意义下是唯一的

5.2.CRT-SSS 算法流程

初始化阶段,设定以下参数：
- s：秘密，$0 \leq s < p$
- p：大素数，$p > s$
- $d_1 < d_2 < \dots < d_n$：n 个两两互素的正整数（作为模数）
- t：门限值
- 满足条件：$d_1 d_2 \cdots dt > p \cdot d{n - t + 2} \cdots d_n$
- 该条件保证任意 t 个份额可恢复出唯一解，而少于 t 个则不够信息恢复。
密钥分发阶段（由分发者执行）
- 选择一个随机整数 $r \in [0, \left\lfloor \frac{N}{p} \right\rfloor - 1]$，其中 $$N = d_1 \cdots d_t$$
- 计算：$s' = s + rp$
- 对每个参与者 $P_i$，计算其份额：$x_i = s' \bmod d_i, \quad \text{for } i = 1, 2, \dots, n$
- 将$ (x_i, d_i) $分发给参与者 P_i，其中 d_i 是公开的。
秘密重构阶段（由至少 t 个参与者协同完成）
- 给定 t 个份额 $(x_{i1}, d{i1}), ..., (x{it}, d{i_t})$，利用中国剩余定理计算 $$s'$$：

$$ \begin{cases}

s' \equiv x_{i1} \pmod{d{i_1}} \\

s' \equiv x_{i2} \pmod{d{i_2}} \\

\vdots \\

s' \equiv x_{it} \pmod{d{i_t}}

\end{cases} $$

恢复出 s' 后，再恢复出秘密：$s = s' \bmod p$

5.3.案例分析

设：

秘密 s=9，门限 t=3，总份额数 n=5
选素数 p=17
选择模数：$$d_1 = 5, d_2 = 7, d_3 = 9, d_4 = 11, d_5 = 13$$
选随机数 r=2

则：