密码学家族：Blum, Blum和Blum

来源: [ 维基百科]

家族密码学：Blum、Blum 和 Blum

我们口袋里的智能手机背后是几十年扎实的研究进展。而这些研究的背后是人。而且，这些人充满热情地解决实际问题并分享他们的知识。而且，有时这项工作是家族式的。

所以，昨天我发表了一篇关于 Lenstra 兄弟对数学和密码学的贡献的文章[ 这里]，所以让我们看看另一个家族：Blum 家族。

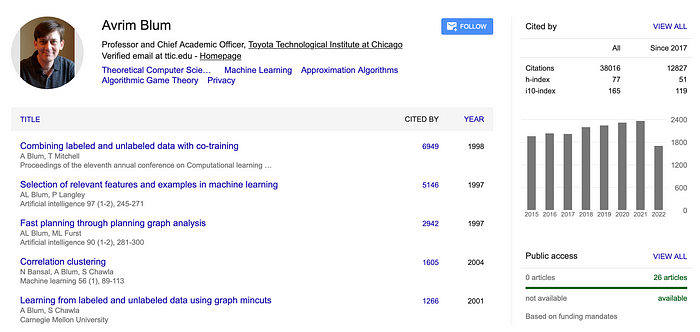
Manuel Blum 和 Lenore Blum 这对夫妇都是卡内基梅隆大学的教授。但是，他们两人都在 2018 年辞职，以抗议研究项目中的性别歧视待遇。Avrim（他们的儿子，也包含在本文顶部的照片中）也遵循了家族路线，成为卡内基梅隆大学的计算机科学教授。事实上，他的博士导师是密码学天才 Ron Rivest。

像他的父母一样，Avrim 在复杂性理论和机器学习的许多领域都取得了进展[ 这里]：

就像他们的儿子一样，Manuel 和 Lenore 为研究领域提供了很多伟大的东西。其中包括 Blum 整数、Blum-Blum Shub 随机数生成器、Blum-Goldwasser 公钥加密系统和 CAPTCHA 的发明。而且，Manuel 也是许多博士生的杰出导师，包括 Len Adleman、Shafi Goldwasser 和 Silvio Micali。这是 Silvio 和 Manual 共同撰写的一篇经典论文：

他是一位鼓舞人心的博士生导师，你可以看出他非常关心他的学生 [ 这里]：

在攻读博士学位时，你必须专注于一个非常狭窄的主题，以便能够完全理解它。一开始，你似乎在研究一根谚语中的针，它是世界的一小部分，是一颗微小的晶体，美丽但从整个事物来看，却是微不足道的。与它一起工作。你越是与它合作，你就越深入地了解它，你就越会发现你的工作，你的主题，包含着整个世界。随着时间的推移，你将会看到你沙粒中的世界。
在一粒沙子里看到一个世界
或在野花中看到天堂，
在你的手掌中握住无限
并在一个小时内握住永恒。
威廉·布莱克 (1757-1827)"

以及不断写作（和学习）的重要性：

我记得麻省理工学院的一位数学教授，
名字叫 BERTRAM KOSTANT，
每当他在办公室时，他都会敞开门，而且他总是坐在书桌前写作。
写作。一直在写作。
他是在写他的研究吗？也许吧。
他是在写他的想法吗？也许吧。
我个人认为他是在阅读，并在写他所阅读的内容。
至少对我来说，写下我所阅读的内容是学习复杂材料最愉快和最有益的方式之一。

我个人认为这是一个很好的建议，因为我写书和我的网站，是因为我正在学习这些主题。

Blum 和 Blum

Manuel 和 Lenore 的第一篇合作论文之一发表于 1975 年 [ [这里](http://Toward a mathematical theory of inductive inference)][1]：

但是，在 1986 年，Lenore 和 Manuel 概述了现有的最好的可证明伪随机数生成器之一……Blum Blum Shub (BBS) 方法 [ 这里]：

它使用的形式是：

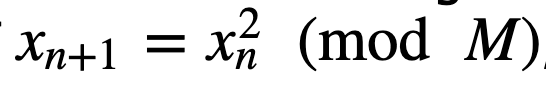
其中 x_0 是一个随机种子。M 的值等于 pq，其中 p 和 q 是素数。p 和 q 的这些值都与 3 模 4 同余（p = q = 3 (mod4) ）。这意味着什么？ 好吧，当我取 p 或 q 的值并将其除以 4 时，我将得到余数 3。

所以，p=7 是可能的（因为 7 除以 4 是 1，余数是 3），p=11 也是可能的（因为 11 除以 4 是 2，余数是 3）。13 的值是不可能的，因为它将是 3，余数是 1。让我们在 Python 中尝试一个简单的例子 [ 这里]：

>>> p=7
>>> q=11
>>> M=p*q
>>> x0=5
>>> x1=(x0**2)%M
>>> x2=(x1**2)%M
>>> x3=(x2**2)%M
>>> x4=(x3**2)%M
>>> print (x1,x2,x3,x4)
25 9 4 16

在本例中，我们使用 p=7 和 q=11，然后使用种子 x_0=5，随机序列是 25、9、4 和 16。我们通常只取最低有效位，所以输出将是“1100”。

该方法的安全性涉及分解 M 的难度。总的来说，它很慢，但它是经过验证的最强大的随机数生成器。对于每个步骤，我们从 x_n +1 中提取一些信息，这些信息通常是最低有效位。它不会在密码应用程序中使用，但可以在密钥生成中使用。

使用的代码是 [ 这里]：

import sympy
import random
import re
import sys
x = 3*10**10
y = 4*10**10
seed = random.randint(1,1e10)

def lcm(a, b):
    """Compute the lowest common multiple of a and b"""  # 计算 a 和 b 的最小公倍数
    return a * b / gcd(a, b)
def gcd(a,b):
    """Compute the greatest common divisor of a and b""" # 计算 a 和 b 的最大公约数
    while b > 0:
        a, b = b, a % b
    return a
def next_usable_prime(x):
        p = sympy.nextprime(x)
        while (p % 4 != 3):
            p = sympy.nextprime(p)
        return p
p = next_usable_prime(x)
q = next_usable_prime(y)
M = p*q
N = 1000

if (len(sys.argv)>1):
    N=int(sys.argv[1])

print "\np:\t",p
print "q:\t",q
print "M:\t",M
print "Seed:\t",seed
x = seed
bit_output = ""
for _ in range(N):
    x = x*x % M
    b = x % 2
    bit_output += str(b)
print bit_output
print "\nNumber of zeros:\t",bit_output.count("0")  # 零的数量
print "Number of ones:\t\t",bit_output.count("1")  # 壹的数量
xi=''
print "\nPredicting 1st 10 with Euler's Theorem:" # 使用Euler定理预测前 10 个
for i in range(10):
    xi += str((seed ** (2**i % lcm((p-1),(p-1))) % M) %2)
print xi

一个示例运行是 [ 这里]：

p:  30000000091
q:  40000000003
M:  1200000003730000000273
Seed:   2188162291
1011001011011110101101110001011000110001000010110110010100011110011010011100000001011111101100100101
Number of zeros:    49
Number of ones:     51

这是我的解释：

Blum 整数

让我们看看 Blum 整数的魔力——它是以 Manuel 的名字命名的。这些与以下形式的求解有关：

y = x² mod n

我们需要为不同的 x 值以及给定的模数 (n) 找到 y 值。例如，如果我们有：

4 = x² (mod 15)

x 的有效值是 2、7、8 和 13。但有时没有解决方案，例如 x=3。

Blum 整数是通过将两个素数（p 和 q）相乘而创建的，其中 p=3 (mod 4) 且 q = 3 (mod 4)：

n=p * q

因此，我们取素数（p 和 q）并将它们除以 4，如果我们得到 3 的答案，我们就得到了所需的值。例如，7 是一个可能的值，因为当我们除以 4 时，我们得到 3。可能的素数是：3、7、11、19 等。然后 Blum 整数变为：21、33、57、69、77、93、129、133、141、161、177、201、209、213、217、237、249、…。

现在，这些具有有趣的属性。首先是当我们确定一个值的模平方根时，我们得到四个平方根。让我用一个例子来说明这一点。假设我有 p=47 和 q=43：

47 = 3 (mod 4) [因为这是 15 r 3]

43 = 3 (mod 4) [因为这是 14 r 3]

我们发现 N 为：

N = 47*43 = 2,021

接下来，我们发现对于 0 到 N 之间的每个值，都有四个平方根值。让我们选择一个值 y =4。为此，4= x²(mod 2021) 中 x 的解是：

1976^2=4 (mod 2021)
  2^2=4 (mod 2021)
  2019^2=4 (mod 2021)
  45^2=4 (mod 2021)

例如，1,972²² = 3,904,576，然后如果我们取 (mod 2,021)，我们得到 4。因此，我们的 Blum 整数总是给出我们四个模平方根。这是一个计算其中一些的小程序 [ 这里]：

import sys
import libnum

p=0
q=0
bitsize=8
if (len(sys.argv)>1):
        bitsize=int(sys.argv[1])

while ((p%4)!=3):
  p=libnum.generate_prime(bitsize)
while ((q%4)!=3):
  q=libnum.generate_prime(bitsize)
print ("\nPrime (p): %d. Length: %d bits, Digits: %d" % (p,libnum.len_in_bits(p), len(str(p)) )) # 素数(p)：%d。长度：%d 位，位数：%d
print ("\nPrime (q): %d. Length: %d bits, Digits: %d" % (q,libnum.len_in_bits(q), len(str(q)) )) # 素数(q)：%d。长度：%d 位，位数：%d

n=p*q
print ("N=",n)
print ("The first few values:") # 前几个值：
for x in range(2,12):
  if (libnum.has_sqrtmod(x,{p: 1,q:1})):
    res=libnum.sqrtmod(x,{p: 1,q:1})
    y=next(res)
    print ("  %d^2=%d (mod %d)" % (y,x,n))
    y=next(res)
    print ("  %d^2=%d (mod %d)" % (y,x,n))
    y=next(res)
    print ("  %d^2=%d (mod %d)" % (y,x,n))
    y=next(res)
    print ("  %d^2=%d (mod %d)" % (y,x,n))
    print ()

这是代码：

blum02 - Python Repl \ \ Skip to content This is Booogle 3. On Booogle 3 you can make notes/tasks, play games and also check the time and more…\ \ replit.com

Blum-Goldwasser 概率加密

使用公钥加密，Alice 可以发送给 Bob 两个可能的消息（“0”或“1”）。如果 Eve 知道可能的消息（“0”或“1”），她将使用 Bob 的公钥对每个消息进行加密，然后将结果与 Alice 发送的密码消息进行匹配。因此，Eve 可以确定 Alice 发送给 Bob 的内容。为了克服这个问题，Blum-Goldwasser 方法是一种公钥算法，它使用概率公钥加密方案 [ 这里][2]：

加密方法使用 Blum-Blum-Shub (BBS) 技术来生成密钥流[ 这里]。最初，我们创建两个素数（p 和 q），然后计算 N：

N = pq

公钥是 N，私钥是 p 和 q，其中 p 和 q：

p (mod 4) = 3

q (mod 4) = 3

例如，我们可以选择 p= 239、q= 179，因为当我们执行 (mod 4) 运算时，两者都会给我们 3：

>>> p=239
>>> q=179
>>> p%4
3
>>> q%4
3

维基百科定义的基本方法是：

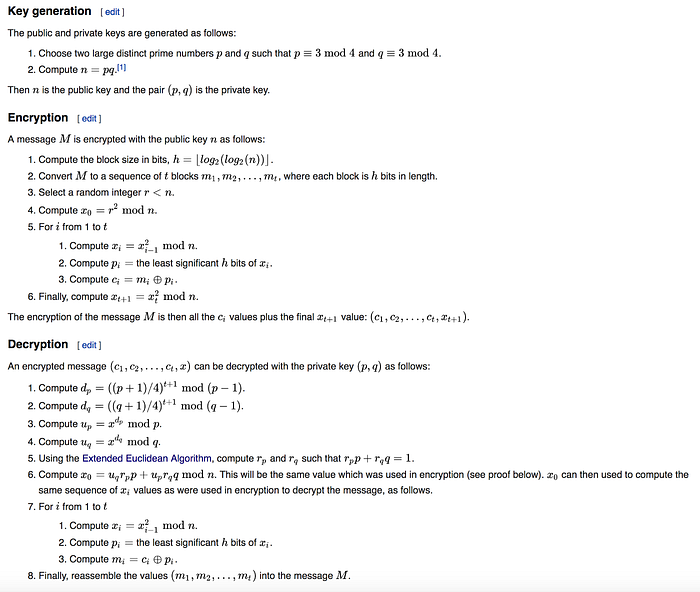
代码如下[ 这里]：

import numpy as np
import binascii
import Crypto.Util.number
from Crypto import Random
import sys
import random

def xgcd(a, b):
    """return (g, x, y) such that a*x + b*y = g = gcd(a, b)""" # 返回 (g, x, y) 使得 a*x + b*y = g = gcd(a, b)
    x0, x1, y0, y1 = 0, 1, 1, 0
    while a != 0:
        (q, a), b = divmod(b, a), a
        y0, y1 = y1, y0 - q * y1
        x0, x1 = x1, x0 - q * x1
    return b, x0, y0

# Method from https://stackoverflow.com/questions/7396849/convert-binary-to-ascii-and-vice-versa
def to_bits(text, encoding='utf-8', errors='surrogatepass'): # 来自 https://stackoverflow.com/questions/7396849/convert-binary-to-ascii-and-vice-versa 的方法
    bits = bin(int(binascii.hexlify(text.encode(encoding, errors)), 16))[2:]
    return bits.zfill(8 * ((len(bits) + 7) // 8))

def from_bits(bits, encoding='utf-8', errors='surrogatepass'):
    n = int(bits, 2)
    return int2bytes(n).decode(encoding, errors)

def int2bytes(i):
    hex_string = '%x' % i
    n = len(hex_string)
    return binascii.unhexlify(hex_string.zfill(n + (n & 1)))

# Derived from https://github.com/coenvalk/blum-goldwasser-probabilistic-encryption/blob/master/blumgoldwasser.py
def BGW_enc(p, q, x, m): # 来源于 https://github.com/coenvalk/blum-goldwasser-probabilistic-encryption/blob/master/blumgoldwasser.py
    n = p * q
    # assert p%4 == 3 and q%4 == 4    
    k = int(np.log2(n))
    h = int(np.log2(k))    
    t = len(m) / h    
    xi = x
    c = ''
    for i in range(t):
        mi = m[i*h:(i + 1)*h]
        xi = (xi ** 2) % n
        xi_bin = bin(xi)
        pi = xi_bin[-h:]        
        mi_int = int(mi, 2)
        pi_int = int(pi, 2)        
        ci = pi_int ^ mi_int
        ci_bin = format(ci, '0' + str(h) + 'b')
        c += ci_bin    
    xt = (xi ** 2) % n
    return c, xt

def BGW_dec(p, q, a, b, xt, c):
    assert a*p + b*q == 1
    n=p*q
    k = int(np.log2(n))
    h = int(np.log2(k))    
    t = len(c) / h    
    d1 = (((p + 1) / 4)**(t + 1)) % (p - 1)
    d2 = (((q + 1) / 4)**(t + 1)) % (q - 1)    
    u = pow(xt,d1,p)
    v = pow(xt,d2, q)    
    x0 = (v*a*p + u*b*q) % n    
    xi = x0
    m = ''
    for i in range(t):        
        ci = c[i*h:(i + 1)*h]
        xi = (xi**2) % n
        xi_bin = bin(xi)
        pi = xi_bin[-h:]
        ci_int = int(ci, 2)
        pi_int = int(pi, 2)        
        mi = pi_int ^ ci_int
        mi_bin = format(mi, '0' + str(h) + 'b')
        m += mi_bin    
    return m

p = 499
q = 547
bits=10
msg='Hello'
if (len(sys.argv)>1):
        bits=int(sys.argv[1])
if (len(sys.argv)>2):
        msg=(sys.argv[2])

while True:
 p=Crypto.Util.number.getPrime(bits, randfunc=Crypto.Random.get_random_bytes)
 if (p%4==3): break

while True:
 q=Crypto.Util.number.getPrime(bits, randfunc=Crypto.Random.get_random_bytes)
 if (q%4==3): break

m=to_bits(msg)
a=1
b=1
_,a,b=xgcd(p,q)
r= random.getrandbits(bits)
x0 = (a*p*r + b*q+r) % (p*q)

c, xt = BGW_enc(p, q, x0, m)

print ("Message: %s" % msg) # 消息：%s
print ("   %s" % m)

print ("\nNo of bits in prime is %d" % bits) # 素数中的位数是 %d
print ("p= %d" % p)
print ("q= %d" % q)
print ("a= %d" % a)
print ("b= %d" % b)
print ("r= %d" % r)
print ("x0= %d" % x0)
print ("ap+bq: %d" % (a*p+b*q))

print "\nCiphertext:", c
d = BGW_dec(p, q, a, b, xt, c)

print ("Decrypted: %s" % from_bits(d)) # 解密：%s

一个示例运行是 [ 这里]：

Message: Hello
   0100100001100101011011000110110001101111
No of bits in prime is 16
p= 65447
q= 34231
a= -7482
b= 14305
r= 37115
x0= 1908144401
ap+bq: 1

Ciphertext: 0011100101011111010000110011100011010010
Decrypted: Hello

CAPTCHA

当然，最后，我们来看看旨在区分人和机器人的在线系统 [3]：

这是将密码学和人工智能领域结合在一起的首批论文之一，Avrim 将继续研究该领域。

结论

研究领域非常感谢 Manuel、Lenore 和 Avrim。没有他们，我们的世界会更加复杂和缺乏信任。有时，密码学是与生俱来的。而对于研究？它存在于他们的 DNA 中：

并且：

参考文献

[1] Blum, L., & Blum, M. (1975). Toward a mathematical theory of inductive inference. Information and control, 28(2), 125–155.

[2] Blum, M., & Goldwasser, S. (1984, August). An efficient probabilistic public-key encryption scheme which hides all partial information. In Workshop on the theory and application of cryptographic techniques (pp. 289–299). Springer, Berlin, Heidelberg.

[3] Ahn, L. V., Blum, M., Hopper, N. J., & Langford, J. (2003, May). CAPTCHA: Using hard AI problems for security. In International conference on the theory and applications of cryptographic techniques (pp. 294–311). Springer, Berlin, Heidelberg.

• 原文链接： medium.com/asecuritysite...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～