二叉默克尔树的结构, Part-1
- EthFans
- 发布于 2020-10-19 15:02
- 阅读 4485
在设计十六进制 trie 时,一些设计选择在当时听起来很棒,但是经过 5 年的实践,被证明带来了很多复杂性。鉴于 ETH 1.x 想要转向二进制 trie,我们正好可以借此机会研究一下状态的存储方式。
过去几个月来,我一直致力于将 trie 从十六进制树结构过渡到二进制树结构。我已经写了一篇关于如何转换状态树格式的文章(中文译本),但是没有完全说明状态树的结构。我将撰写一系列文章来探讨设计新结构时需要做出哪些权衡。本文是该系列的第一篇。
在设计十六进制 trie 时,一些设计选择在当时听起来很棒,但是经过 5 年的实践,被证明带来了很多复杂性。鉴于 ETH 1.x 想要转向二进制 trie,我们正好可以借此机会研究一下状态的存储方式。
问题的根源
在重新设计存储格式时,我们至少可以从 5 个方面进行改进。
-
将账户 trie 和存储 trie 合并:维护多个结构会增加复杂性,典型的例子就是节点必须先遍历账户 trie,得到存储 trie 的根,然后再到存储 trie 上获取数据。
-
扩展节点(extension nodes):这是一种特殊的节点,负责给特定子树上的所有 key 加上前缀。这些节点的作用是能够限制需要被哈希的节点数量,但是也引入了复杂性,因为它们所涉及的 key 必须以特定方式打包。
-
RLP 编码格式旨在高效地对任意结构进行编码。由于其复杂性,它也带来了很多麻烦:必须费尽千辛万苦打包 key 块(pack key chunk)。另外,由于每个节点的结构相当固定,可以使用更简单的序列化方法来代替 RLP。
-
与前两个问题相关的是,十六进制的前缀也会带来复杂性和混乱。
-
十六进制 trie 的证明【即,“见证数据(witness)”】比二进制 trie 的证明大 4 倍左右。(欲知详情,请阅读这篇文章。(中文译本))
RLP —— Ramble, Lose yourself and Pester?
(译者注:“RLP” 是 “Recursive Length Prefix(递归长度前缀)” 的缩写,但作者这里使用了几个 R、L、P 开头的词 “漫无目的、迷失自我、喋喋不休”,就是批评之意。 )
本文我们会讨论怎么解决 RLP 问题。如果 RLP 被取代,绝大多数核心开发者都不会感到伤心。这是因为 RLP 过于复杂。实际上,我听过的唯一一个支持保留 RLP 的理由是:“RLP 实在太过复杂,不要再冒险选择新的格式了,以免重蹈覆辙。”
RLP 的基本原理是采用简单的 size + data 格式。这就是复杂性的由来。首先,size 可以是任何整数(实际上,它不可能超过 2 字节,但是从原则上来说是可以的,因此你必须确保能够支持超过 2 字节的 size)。我们如何知道 size 部分在哪里结束,data 部分在哪里开始?
-
在大多数情况下,开头会加上一个 header。这个 header 是一个值
h,然后再加上 size 值:因此,RLP 编码是[length(data)+h] [data] -
如果
length(data)+h < 256,则 RLP 编码如上所示。如果数据太大,加上h值后超过一个字节,该怎么办?没错,你还需要再增加一个字节,即,引入h'值来表示你正在使用第二种存储方案。在这种情况下,RLP 编码是[h'+length(length(data))] [length(data)] [data]。为 “方便” 起见,h'被选定为 56。 -
如果数据大小为一个字节,你发现自己必须在这个字节前再增加一个字节。有没有可能不这样做?部分情况下可以,但是会另外增加复杂程度!如果
data[0]< h,那就不需要增加 header。相应地,任何以小于h的值作为开头的字节负载必定只有一个字节。
还能再酸爽一点吗?当然可以了!RLP 涉及两类 “对象”:结构列表和字节数组。
- 字节数组:header=128,overflow_header=183
- 结构列表:header=192,overflow_header=247
请注意,data size 部分的最大规模是 8 bytes,也就是一个 64 bits (原文为 “64-bytes”,应有误)的数字。确实,无论什么数据,18014398509481984 KB 应该都够用了。
虽然还有很多棘手的细节有待深入,但要点看起来很清楚了:RLP 难以驯服。我们再来看看它是如何与状态树交织在一起的。
默克尔化规则(Merkelization rule)
我们怎么把 RLP 编码和它那令人厌烦的逻辑用到我们的默克尔化规则中?先从默克尔树底部的叶子节点开始说起。
叶子节点及其十六进制前缀
叶子节点保存了一个值(value),在这个值前面还有一个不知道多少位的键(key),这个键跟其它叶子节点的键肯定是不一样的。因此,我们有了一个元组 (key, value),这就是一个包含两个元素的列表,包含了 key 和 value,两个数据都是字节数组(byte array)。RLP 理论上应该能帮助我们编码这两个数据吧?不那么见得。
一棵十六进制树上的 key 是基于半字节(nibble-based)的,所以如果我们取出一个键的时候,它可能在半字节处就中止了,那问题就来了:我该怎么对齐数据呢?这里面必须要有一个设计抉择。结果是,我们使用一种叫做 “十六进制前缀(hex prefix)方法” 的函数来读取键数据,它会加入一个 header 来告诉我们所读的键的长度究竟是偶数个还是奇数个半字节。

- 十六进制前缀编码方法使用第一个字节(即上文的 “头字节”)中的前半个字节来存储该键的长度(是奇数还偶数个半字节)。 -
十六进制前缀方法还要求我们调整半字节的位置。举个例子,如果键的长度是奇数个半字节,那就把第一个半字节放到头字节的最后一个半字节的位置。
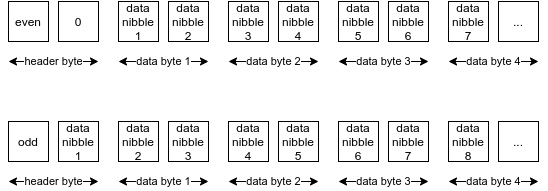
同样地,如果长度是奇数,但跟字节的终止位置对不齐(not byte-aligned),那么每一个半字节都必须位移,以使其能以少一个字节的长度来存储。
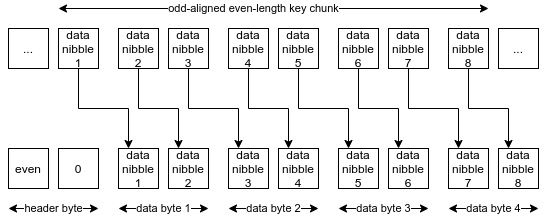
- 如果长度是偶数,但却是奇数对齐的(odd-aligned),那所有的半字节都要位移 4 个位。 -
所以,叶子节点最终是以 RLP(HP(key_chunk), value) 的形式来编码的。
分支节点和太小的子节点
一个分支节点(branch node)有 16 个子节点(childeren),每个字节点都占用半个字节。按照 RLP 的规则,分支节点只是一个其子节点哈希值的列表,也就是一个包含了 16 个字节数组的列表。如果某个子节点是空的,那就表示为一个空的数组(只是用一个独立的 128 来标注一个长度为 0 的数组)。世界上,列表中还有第 17 个条目,就是分支节点本身的值,但因为实践中都不使用它,所以列表的最后一个条目总是 128。
没错,正如你所料,这里又会产生很多麻烦。为了避免在数据库中为太小的对象创建条目,一个 RLP 编码值太小的节点就不会计算出哈希值。在这种情况下,其 RLP 编码会直接存储为一个原始数据的列表,而不是这个列表的哈希值。结果就是你在列表中鲜少找到数组开始的标记(128),反而常常找到另一个列表开始的标记(192),又给开发者出了很多难题。
如果一个分支节点的 RLP 的数据总大小大于 32,那它就会被算成哈希值。大部分时候都是如此,因为,如果没有算成哈希值,那就意味着一个子节点的 RLP 数据大小已达最大值:16 个字节。
延伸节点
状态树上还有第三种节点,叫做延伸节点(extension node),我们放在下一篇文章中集中讨论。幸好,幸好,在 RLP 编码这一点上,它没有给我们增加任何麻烦。
我们真的需要 RLP 吗?
所有这些优化都是有用的吗?不见得呀。
举个例子,假如我们不使用 rlp < 32 bytes 这条规则,需要多占用多少存储空间呢?

跟今天全同步节点所需的约 300 GB 的存储空间相比,简直是微不足道。
类似地,不使用十六进制前缀编码,也只会导致多占用 100 MB 的存储,也就是多占用 0.03%。只要仔细选择二进制 trie 的编码格式,这点差距就可以补回来。
二进制 trie:送 RLP 入土为安
在二级制 trie 上,分支节点会变得简单很多:一个节点最多只有两个子节点,可以由其哈希值来指出。一个 Keccak256/Sha256 的哈希值,也就是 32 个字节。
在当前,显然的事情是,我们根本不需要一个能编码任意长度的值的通用编码方案。举个例子,假设新的二进制树种的每个节点都具有下列的字段:
- 左子节点哈希值,用作指针;
- 右子节点哈希值,用作指针;
- 值(可选),即存储在用于寻得此节点的键中(stored at the key used to get to this node)的值
- 前缀(可选),目的是替换十六进制 trie 中的延伸节点
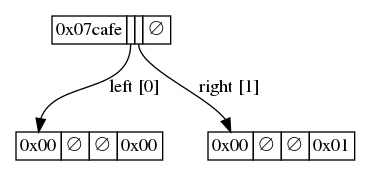
- 例子中的树存储着键值对 (0xcafe, 0x00) 以及 (0xcaff, 0x01):根节点以键数据 “0xcafe” 和一个数字作为前缀;该数字表示最后一个字节中仅有 7 个比特用于存储前缀。然后该节点有两个指针指向其两个子节点,同时不包含值。每一个子节点都以空值为前缀(以 0x00 为标记),都有一个值,都没有子节点。 -
客户端可以用只占两个字节的 header 来编码这个节点的数据:
 <center> 中间节点序列化头提案 </center>
<center> 中间节点序列化头提案 </center>
这个模式只需额外占用两个字节,相比之下,RLP 则至少需要 5 个字节。第一个字节包含下列标签:
- 如果 #7 bit 为有,则此 header 后面所跟随的数据的前 32 个字节即是左子节点的哈希值。如果该比特为空,则左子节点的哈希值也为空。
- 如果 #6 bit 为有,则跟着的 32 个字节表示右子节点的哈希值。如果该比特为空,则右子节点的哈希值也为空。
- 如果 #4 bit 为有,则该 header 会有一个额外的字节来给出前缀比特中的数字;前缀比特则跟着 左/右 子节点哈希值放置;
- 如果 #5 bit 为有,则 header 后载荷剩下的字节就用来表示该值
这个方法的一个重点是,它同样也覆盖到了十六进制前缀编码的功能,因此后者也可以取消掉了。
结论
我承认,在解释 RLP 的工作模式时,我一直在发泄使用 RLP 时累积的挫败感。
客观来说,这个设计其实并不差,而且在过去五年的使用中毫无疑问也达到了它的设计目的。但随着时间推移,变得越来越清楚的是,其复杂性是一个过于昂贵的代价,我希望能说服你,在与存储树相关的部分中,取代 RLP 是利大于弊的。
本文中所描述的存储树格式也远远称不上完备,我们会在日后介绍更多侧面。
非常感谢 Sina Mahmoodi 和 Martin H. Swende 的反馈。
原文链接: https://medium.com/@gballet/structure-of-a-binary-state-tree-part-1-48c587836d2f 作者: Guillaume Ballet 翻译&校对: 闵敏 & 阿剑
- 基于哈希函数的签名(四):XMSS 和 SPHINCS 597 浏览
- 基于哈希函数的签名(三):多次签名 757 浏览
- 64 字节长的比特币交易 1250 浏览
- 区块链密码学基础概念 2642 浏览
- 用于验证 Taproot 资产转移的虚拟机执行环境 1569 浏览
- Merkle Patricia Trie 简介 1613 浏览
- 不可重用证明1 985 浏览
- bips/bip-tap-proof-file.mediawiki,位于 bip-tap · Roasbeef/bips 1346 浏览
- 空投大杂烩 - 合约实现空投发放的三种方案 3602 浏览
- ariard/bips 的bips/bip-merklesub.mediawiki,提交版本号为ddb77158a8309f307faaaf643830e4d0f07b90d3 1682 浏览
- bips/bip-tap-universe.mediawiki,位于 Roasbeef/bips 的 Taproot 资产宇宙 1151 浏览
- 比特币 - bips/bip-tap-ms-smt.mediawiki,位于Roasbeef/bips - Roasbeef 1125 浏览

