随机性、签名脚本和交易可延展性
- enigbe
- 发布于 2022-04-20 17:39
- 阅读 1000
本文解释了比特币交易签名的基本数学原理,阐述了为什么不同的签名脚本可以应用于同一交易,以及隔离见证(SegWit)如何修复交易可延展性问题。文章分析了签名过程中随机数 k 的作用,以及恶意用户如何通过修改签名脚本来改变交易ID,最后说明SegWit通过将签名数据移至见证字段来解决此问题。
隔离见证伴随着它的激活带来了一系列的变化,包括修复交易可延展性——即一个交易的标识符(交易的 SHA256 哈希值)在底层交易没有变化的情况下发生变化的能力。一个交易对象通常包含以下字段:版本,交易输入(包含先前哈希值、先前索引、签名脚本和序列),交易输出(包含金额和公钥脚本),以及锁定时间。
除了签名脚本以外,这些字段在不使交易无效的情况下都无法更改。包含解锁脚本的字段在交易被哈希之前会被清空(签名不应该签署自身),因此可以在不使交易失效的情况下更改解锁脚本。由于这个原因,不同的解锁脚本可以代表同一个交易。这是怎么回事呢?最初,我认为这与签名的计算方式有关,因为随机性嵌入在用于签署交易的签名算法中。
从我的角度来看,理解签名过程的基本底层数学原理可以提供一些见解。因此,在本文中,我将解释我对签名基本数学原理的理解,不同的签名以及扩展的解锁脚本如何应用于同一交易,以及隔离见证如何修复交易可延展性。
签名的基本数学原理
签名是一种证明知晓和拥有一个秘密数字(即私钥/签名密钥 e)而不泄露这个数字的方式。我们知道在非对称加密系统中
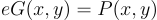
公式 1:从私钥和生成器点计算公钥
其中 G 是生成器点,P 是公钥。
为了签署一个交易哈希,选择一个随机数 k,使得
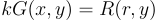
公式 2:计算签名的 r 值
我假设因为 G 位于椭圆曲线上,所以 R 也位于其上,因此曲线上两个点的总和将给出 R 的位置(加法在有限域中是封闭的)。这些点 (u, v) 可以由签名者选择,如下图所示。
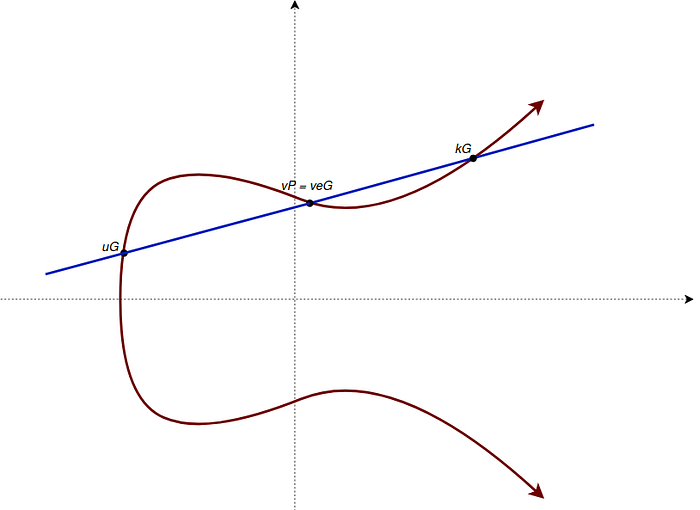
图 1:椭圆曲线上的 uG、vP 和 kG 点
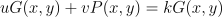
公式 3:离散对数问题 (DLP)
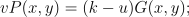
知道 eG = P,并重新排列
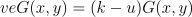
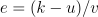
公式 4:签名的目标
公式 4 可以被认为是表示离散对数问题(DLP)的另一种方式,因为你要么知道 e,选择 k 使得 (k — u)/v 等于 e(从而解决 eG = P),要么尝试暴力破解方法,通过选择 (k, u, v) 的几种组合。
在为交易生成有效的签名 S(r,s) 时,我们:
- 对交易进行哈希以获得 z(交易哈希)——注意清空解锁脚本并附加适当的签名哈希标志,
- 选择一个随机的唯一的 k,
- 计算 kG = R(r,y) 并选择它的 x 坐标 (r),
- 并计算 s,以便通过选择如下所示的 u 和 v 将交易哈希 (z)和签名密钥 (e) 合并到签名中:
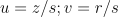
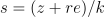
组合 r 和 s 可以为交易提供有效的签名。
为什么不同的签名脚本可以应用于同一个交易
可以看出,任何满足该等式的 k(对于签名必须是唯一的)、u 和 v 的组合对于给定的交易哈希 z 都是有效的。从签名者的角度来看,这很好。一个交易的签名者可以多次签署该交易,为该交易生成不同的有效签名。然后将该签名嵌入到交易的签名脚本中,然后广播到网络。
然而,网络上的一些恶意用户可以接收广播的交易,并以不同的方式修改它,以生成一个新的有效但可延展的交易,该交易本质上与最初广播的交易相同,只是具有不同的交易 ID。这些交易花费相同的输入,将相同的值转移到相同的输出,从而产生冲突,只有其中一个交易会被挖掘并添加到账本中。如果可延展的交易被挖掘,则引用原始交易输出的其他交易无法从中花费。
这种交易可延展性是如何实现的?恶意用户可以修改签名格式、向签名脚本添加额外的指令,或在签名脚本上使用加密技巧(Rosenbaum,2019)。基本上,通过更改交易的签名脚本(这会更改序列化的交易和交易标识符)。
隔离见证和修复交易可延展性
隔离见证提议将签名脚本数据移动到另一个字段——见证字段——该字段不用于计算交易 ID,因此对签名脚本字段的更改不会影响交易标识符。
结论
随机性和每个签名选择唯一的 k 值允许签名者改变交易对象。他们可以为一个交易生成不同的签名,尽管选择了一个并将其嵌入到解锁脚本中。在广播他们的签名交易时,在隔离见证之前,用户可能会遇到可延展性攻击,该攻击允许恶意用户修改广播交易的签名脚本字段并更改交易的标识符。通过隔离见证,将数据从签名脚本移动到一个不影响交易 ID 计算的字段中,消除了可延展性攻击向量。
注意:
我非常感谢你能提供的任何反馈。如果你觉得这篇文章有帮助/有用,或者发现事实上的错误陈述,请随时在此处或在 Twitter 上 @engb_os 发表评论或与我联系。
参考文献
- Antonopoulos, A. (2017). Mastering bitcoin: Programming the open blockchain
- Song, J. (2019). Programming bitcoin: Learn how to program bitcoin from scratch
- Rosenbaum, K. (2019). Grokking Bitcoin
- 原文链接: enigbe.medium.com/random...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- Solana 系统调用:sBPF 汇编中的日志记录 192 浏览
- 不要在家中存放加密货币 470 浏览
- 使用 Ecash 票据的谨慎日志合约 397 浏览
- Fiat-Shamir 启发式非交互式零知识证明之美(以及 Zig) 641 浏览
- DahLIAS:既非 ECDSA,也非 Schnorr 610 浏览
- 《比特币开发哲学》:扩容 953 浏览
- 《比特币开发哲学》:升级 1769 浏览
- 安全研究人员的数学指南 919 浏览
- 比特币是如何运行的 2544 浏览
- 构造与破解SIDH 1284 浏览
- 第4章:以太坊钱包 1678 浏览
- 椭圆曲线深入研究(第10部分) 1849 浏览

