关于区块提议者时序博弈与规模经济 - 经济学

关于提案者时序博弈和规模经济

时序博弈 是一种已知的现象（[1]，[2] 和 [3]）。 令人担忧的是，提案者时序博弈会对网络产生负面影响。

在下文中，我想展示参与提案者时序博弈的成功也是规模经济的一个函数。

主要发现是：

→ 拥有 30% 市场份额的实体可以比 5% 的实体延迟 0.8 秒。

→ 验证者市场份额每增加 1%，区块提议的延迟可以增加 0.03 秒，而不会面临额外的重组风险。

特别感谢 Anders、Mike 和 Caspar 的反馈！

介绍

提案者必须收集至少 40% 的选票，以确保他们的区块被接受，并且不会被随后的提案者重组。 这是 40%，因为那是提案者 boost 阈值。 证明少于 40% 的区块可能会被下一个利用提案者 boost 的提案者重组。 对于时序博弈参与者来说，挑战在于确定提议（或调用 getHeader）的最佳时间。 在经济上理性的验证者会希望尽可能地等待（为构建者提供尽可能长的时间窗口），而不会冒重组的风险。

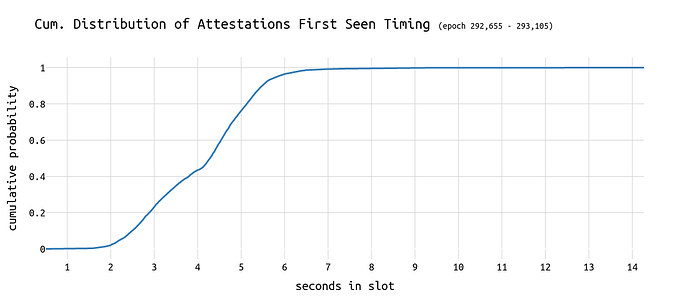
首先，让我们回顾一下来自 此分析 的以下图表：

\ 42fe46361f7b2a22bd61c0195f719a57df04d64d1200×530 27.5 KB

在 slot 中的第 5 秒之前，可以看到大约 80% 的所有证明。 40% 的阈值在 3.8 秒左右达到。 因此，假设零延迟，在 3.8 秒发布的区块应该仍然能够收到 60% 的证明。

在下文中，我们将此曲线称为 C(t)。

初始设置

核心思想是确定验证者在 slot 中累积投票的演变方式，以及提案者对这些验证者的一部分的控制如何影响其区块提案的最佳时机。

鉴于 C(t) 表示时间 t 之前投出的选票的累积百分比，提案者控制 x\% 的验证者，并且需要确保他们在提议时仍然可以达到至少 40%，我们从以下条件开始：

x + (1 - C(t)) \times (1 - x) \geq 0.4

在这个等式中：

• (1 - C(t)) \times (1 - x): 来自不受提案者控制的验证者的剩余未投出的选票，可以支持提案者的区块。

请注意，x \times C(t) 将是提案者的验证者已包含在 C(t) 中的选票部分。

需要强调两个假设：

• 协调：假设验证者在证明时进行协调，例如，使用提供命令的中央 oracle。
• 诚实验证者：在区块提议时尚未投票的所有验证者都将投票支持提议的区块（而不是父区块）。 请参阅 诚实验证者规范。

简化等式

我们重新排列初始等式以找到 C(t) 的阈值，即提案者必须采取行动之前可以投出的选票的累积百分比：

x + (1 - C(t)) \times (1 - x) \geq 0.4

展开并简化：

(1−C(t))×(1−x) = 1 - x - C(t) + C(t) \times x

1 - C(t) + C(t) \times x \geq 0.4

最后，求解 C(t)：

C(t) \leq \frac{0.6}{1 - x}

在此处查找完整的推导 此处。

解释

这个简化的等式 C(t) \leq \frac{0.6}{1 - x} 意味着，只要累积证明 C(t) 保持低于 \frac{0.6}{1 - x} 定义的阈值，提案者就可以安全地提议。

• C(t): 在时间 t 之前投出的选票的累积百分比。
• x \%: 提案者控制的总验证者的百分比。
• 0.4: 确保多数所需的 40% 阈值 (1-0.4=0.6)。

该等式确保提案者凭借其验证者份额，仍然可以通过在累积证明超过此阈值之前提出建议来有利地影响结果。

与小规模运营商相比，拥有许多验证者的节点运营商可以冒险多几秒钟，因为他们知道自己的验证者永远不会投票反对他们。

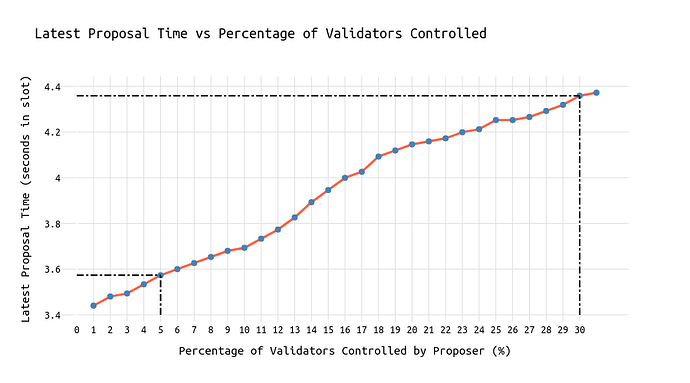
下图显示了规模经济的影响，并回答了以下问题：拥有 x% 市场份额的节点运营商最多可以等待多长时间，直到无法再收到至少 40% 的所有证明。

\ timing_games_proposer_share900×500 30.3 KB

y 轴上的“slot 中的秒数”值是 attestation_seen 时间戳，这些时间戳没有通过区块传播和验证所需的时间进行校正。 由于这些数字只是影响 y 轴上绝对值的常数，因此在使市场份额对时序博弈限制的相对影响可见方面，这无关紧要。

我们可以看到，拥有 30% 市场份额的节点运营商可能比拥有 5% 市场份额的节点运营商多等待 0.8 秒，同时冒着相同的风险。

在 Python 中

使用 Python，我们可以计算出不同验证者控制百分比的最新“安全”提议时间。 这是实现的关键部分：

import numpy as np
from scipy.interpolate import interp1d

## 提供的累积证明数据（秒，已投证明的百分比）
data = [\
     (0.791, 0.0005390835579514825),\
     # (为了简洁，省略了其他数据点)\
     (2.228, 0.05444743935309973),\
     (2.464, 0.10835579514824797),\
     (2.639, 0.16226415094339622),\
     (2.777, 0.21617250673854446),\
     (2.932, 0.27008086253369273),\
     (3.104, 0.323989218328841),\
     (3.308, 0.3778975741239892),\
     (3.627, 0.43180592991913747),\
     (4.069, 0.4857142857142857),\
     (4.25, 0.539622641509434),\
     (4.407, 0.5935309973045823),\
     (4.576, 0.6474393530997304),\
     (4.723, 0.7013477088948787),\
     (4.898, 0.7552560646900269),\
     (5.039, 0.8091644204851752),\
     (5.245, 0.8630727762803234),\
     (5.521, 0.9169811320754717),\
     (6.187, 0.9708894878706199)\
]

## 提取时间和累积证明百分比
times = np.array([point[0] for point in data])
cumulative_attestations = np.array([point[1] for point in data])

## 插入累积证明函数
cumulative_attestation_func = interp1d(times, cumulative_attestations, kind='linear', fill_value="extrapolate")

## 用于计算具有 x% 控制权的提案者可以安全地提议区块的最晚时间的函数
def calculate_latest_proposal_time(x):
    threshold = 0.5 / (1 - x)

    for t in np.linspace(times[0], times[-1], 1000):
        if cumulative_attestation_func(t) > threshold:
            return t
    return None

结论

通过理解和计算验证者市场份额与累积证明之间的关系，提案者可以优化他们的提议时序，从而最大限度地减少重组的可能性，同时最大限度地提高利润。

可以通过检查后续验证者运行的 CL 客户端，或者更简单地检查 epoch 中的 slot 索引来改进此类策略。 基于这些信息，可以更好地估计被重组的几率（例如，如果是 Teku、Nimbus、Lodestar 或 epoch 中的最后一个 slot，那么重组概率会显着降低，因为没有实现诚实的重组策略）。

将提案者时序博弈推向极限会对证明者产生负面影响，并且会产生连锁反应：如果验证者意识到由于他们过于频繁地投票支持错误的区块而错失了利润，他们可能会开始延迟他们的证明。

最终，将时序博弈推向极限可能会对网络产生不利影响。 此外，不应容忍/支持超出从单个节点运行多个验证者的验证者协调。 现在，重要的是关注/贡献区块构建研究，并找到降低时序博弈盈利能力或完全阻止它们的方法。

• 原文链接： ethresear.ch/t/on-propos...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～