区块构建不仅仅是背包问题!- 权益证明/区块提议者
- 以太坊中文
- 发布于 2024-06-20 17:58
- 阅读 772
本文对区块链中的区块构建问题进行了形式化建模,证明了区块构建至少是背包问题和最大独立集问题的结合,因此属于NP-hard问题。接着,提供了几种具有不同权衡的贪婪算法,并通过模拟结果验证了这些算法。结果表明,通过已知背包约束调整贪婪解,在费用收益方面优于当前使用的贪婪算法约15%。最后,讨论了这在以太坊中对区块构建者的实际意义,并提出了未来研究方向。
特别鸣谢 Gabearro Ventalitan Nerla Yun Qi 和 Surya 提供的所有氛围和讨论!
这个项目是上周在 IC3 训练营中完成的一个黑客马拉松项目。
TL;DR
我们提出了区块链中区块构建的正式模型。我们证明了区块构建至少是背包问题和最大独立集问题的结合,从而表明区块构建是一个 NP 难问题。接下来,我们提供了具有不同权衡的各种贪婪算法。然后,我们展示了模拟结果来证明算法和基准的合理性。我们的结果表明,通过已知背包约束的结果调整贪婪解决方案,在获得的费用方面优于当前使用的贪婪算法约 15%。最后,我们讨论了这在实践中与以太坊中的区块构建者的相关性以及未来的研究方向。
介绍
以太坊中的区块构建已经发展成为一个价值数百万美元的产业,尤其是在引入 MEV-Boost 之后。这大大增加了构建者获得的收入。但是,构建者选择交易和交易捆绑的算法还需要更多的研究。Mikerah(项目组长)与 Flashbots 合作,最近从事一个项目,该项目将区块构建的模型形式化为背包问题。该模型考虑了每笔交易的效用(交易提供的费用)和成本(交易使用的 gas),以及可以支付的最高价格的预算(区块的 gas 限制)。这项研究的实际意义是显而易见的,因为它解决了当前模型的一个重大限制,即并非所有交易都是彼此独立的。
问题
让我们深入探讨问题的核心,研究为什么交易不是独立的,这是区块构建中的一个关键挑战。
比特币区块链
中本聪区块链论文中描述的最关键的问题是捕捉双重支付。如果两笔交易试图花费相同的 UTXO,则只有其中一笔应该上链。因此,我们可以看到某些交易是相互依赖的。但是,这还不是全部。某些与比特币的 OP-Code 设计交互的交易也可能相互依赖。一个经典的例子是,在 HTLC 中,退款交易(通过显示哈希的预映像来发布)或付款(当交易上的时间锁过期时发布)都可以通过。如果这两个交易同时存在于 mempool 中,则这些交易会相互冲突。
以太坊区块链
以太坊继承了双重支付交易问题,但是由于其智能合约和 gas 费设计,它仅部分受到另一种冲突类型的影响,因为费用是根据使用的 gas 量支付的。这导致模型略有变化,即支付的费用和使用的 gas 量取决于其他链上交易。此外,在搜索者的存在下,某些交易被捆绑在一起,以使多个捆绑包包含相同的交易,因此不能同时将其包含在区块中。
模型
在描述数学公式之前,我们首先介绍我们所做的假设。
假设
- 相关的费用和 gas 难以建模,因为我们无法获得布尔表示形式。因此,我们仅考虑“冲突”,而涉及“依赖关系”。冲突是指交易不能同时发生的情况,而依赖关系是指一个交易需要另一个交易在其有效之前执行的情况。
- 我们进一步忽略了区块内交易的最佳排序。按特定顺序对交易进行排序可能会由于 MEV 而导致更高的利润,出于与上述相同的原因,我们忽略了这一点。
- 对于以太坊,在 EIP 1559 的条件下,所考虑的费用是高于基础费用的部分。任何具有负费用的交易都将被忽略。
鉴于这些假设,我们现在对具有约束和依赖关系的二进制分配问题建模如下:
令 TT 为交易集。TT 中的交易表示为 tx_itxi。
令 f_ifi 表示与交易 tx_itxi 相关的费用。
令 g_igi 表示与交易 t_iti 相关的 gas
令 BB 为最大区块 gas 限制。
那么,我们有以下优化问题
最大化
\sum_{i\in n} f_ix_i
主题是
\begin{align*} &\sum_{i\in n} x_ig_i \leq B \\ & x_i+x_j \leq C_{ij}, \forall i\neq j \in n\\ & x_j - x_i \leq M_{ij}, \forall i\neq j \in n\\ & x_i \in \{0,1\} \end{align*}
其中,
- 如果 t_iti 和 t_jtj 是冲突交易,则 C_{ij} = 1,否则为 2
- 如果 t_jtj 依赖于 t_iti 并且只能在 t_iti 之后分配,则 M_{ij} = 0,否则为 1
由于实际上,区块构建者很难在其订单流池中交易有限的快照中推断出第三个条件(而无需执行所有交易),因此我们可以省略第三个约束以简化问题。如果构建者遇到这样的交易,则该交易将被视为无效。
因此,我们可以获得以下简化的优化问题
最大化
\sum_{i\in n} f_ix_i
主题是
\begin{align*} &\sum_{i\in n} x_ig_i \leq BL \\ & x_i+x_j \leq C_{ij}, \forall i\neq j \in n\\ & x_i \in \{0,1\} \end{align*}
其中,
- 如果 t_iti 和 t_jtj 是冲突交易,则 C_{ij} = 1,否则为 2
规约
现在,我们提出正式的论点,说明为什么区块构建是背包问题和最大独立集问题的一个实例。
规约到背包问题
将上述问题规约到背包问题很容易理解。我们假设任何交易之间都不会发生冲突。在这种情况下,该问题与解决背包问题相同,实用性是交易支付的费用,占用的空间是交易使用的 gas,最后,区块的 gas 限制确定了背包的大小。因此,区块构建问题至少与背包问题一样困难。
规约到最大独立集问题
如果我们可以解决以上区块构建问题的实例,而没有任何限制多项式中区块大小的约束,则考虑以下实例,其中区块 gas 限制设置为 mempool 中所有交易的 gas 总和。这意味着有足够的空间容纳 mempool 中所有交易。现在,此问题等效于找到最大权重独立集,因为我们可以将所有交易都视为顶点,并且如果对应的交易冲突,则两个顶点之间存在一条边。以上规约创建了最大权重独立集问题的实例化,该问题再次被称为 NP-hard。
近似结果的算法
如上所述,区块构建是一个 NP 难问题,可以规约到背包问题和最大权重独立集问题。由于我们知道最大权重独立集问题没有 C 近似值,这意味着区块构建问题也没有 C 近似值。
因此,我们设计了几种贪婪算法,以便在实践中解决区块构建问题。
经典贪婪算法 (GC)
我们希望今天的构建者使用我们提出的第一个算法。它遵循最广泛使用的背包贪婪解决方案,其中所有对象都根据其效用成本比进行排序,然后贪婪地将空间分配给每个对象,直到你无法再分配更多空间为止。由于增加了冲突约束,因此构建者必须检查与已添加到区块的任何交易是否存在冲突。因此,该算法的工作方式如下:
算法输入: T = \{t_i\}, F = \{f_i\}, G = \{g_i\}
算法输出: gas 使用量小于 BL 的排序区块
算法描述:
Sort T by corresponding F/G
Let B := {}
Let BS := 0
For each t in T, f in F, g in G do:
if t has any conflict with tx in B: continue;
if g + BS < BL: B.append(t); BS += g
return B实际上,仅当按顺序模拟时才知道交易之间的冲突。我们对如何建模此冲突提出了两个约束。
- 如果交易不能一起执行,则两个交易 t_1t1 和 t_2t2 冲突。如果某个地址试图重复花费它拥有的一些资金,或者如果两个搜索者捆绑包试图从交易中提取 MEV,则可能发生这种情况。我们称这种冲突为“真实”冲突。
- 如果两个交易 t_1t1 和 t_2t2 与同一地址进行交互,则它们会冲突。我们称这种冲突为“全部”条件。这些交易不一定会使彼此无效。但是,由于此冲突比另一个约束(gas 大小操作)更容易确定(恒定大小操作),因此我们将其保留为潜在的冲突条件,因此对于基于所用计算时间进行优化的构建者来说,这可能会有所帮助。
注意:在解决方案模拟中,我们假设 “全部” 冲突中的 p=0.95p=0.95 交易不在“真实”冲突中。
根据冲突的定义,我们提出了两个基准贪婪解决方案,我们将其标记为 CG All 和 CG Real。
背包贪婪算法
上面描述的贪婪解决方案不是一个好的近似解决方案。回顾一下背包问题,通过比较上述经典贪婪算法与未分配的第一个对象的效用,我们获得了优于最佳解决方案的 1/2 近似值。
该算法首先运行经典贪婪算法的实例。然后,它找到收益最高的(最高的 f/g)交易并将其添加到区块中。添加此交易将需要修改区块,因为区块 (B) 中的某些交易与此交易冲突,或者由于空间不足而无法插入该交易。因此,我们删除与此新添加内容冲突的交易,然后腾出足够的空间以添加此交易。插入交易后,我们重复进行贪婪插入,直到区块再次满为止。我们重复上述算法,直到我们在贪婪解决方案中至少看到每个交易一次。
该解决方案的伪代码如下:
Sort T by corresponding F/G
Let B := {}
Let B_f:= {}
Let S := {}
Let BS := 0
while S != T:
let t := t in T, not in S, with maximum f/g:
remove any transaction from B that conflicts with t.
remove smallest f/g txs until there is space to insert t.
B.append(t)
S.append(t)
For each t in T, f in F, g in G do:
if t has any conflict with tx in B: continue;
if g + BS < BL: B.append(t); BS += g; S.append(t)
if sum(B.f) > sum(B_f.f): B_f = B
return B_f
## B.f is the fee corresponding to each transaction in B在此贪婪协议中,我们尝试每次都强制包含交易。它仍然不同于贪婪背包 1/2 近似值,但是它试图复制背包贪婪算法所完成的工作,但适用于贪婪算法未选择的所有项目。
此解决方案将优于其经典贪婪算法,因为它计算所有解决方案的最大值,其中之一是经典贪婪解决方案。与经典贪婪解决方案一样,当冲突为“真实”和“全部”时,我们会分析此解决方案。
经典贪婪信息解
与所有已知的 NP-Hard 问题(尤其是我们一直在施加的最大独立集条件)相比,解决背包问题非常容易。因此,我们允许构建者通过 BLP 求解器合理地准确和快速地解决背包问题。背包解决方案使构建者对如何构建区块有所了解,然后,当所选区块中存在冲突的交易时,便会丢弃“稍后”的交易。在此解决方案中,我们运行背包 LP 解决方案。在 LP 的输出上,我们基于 i) f/g 比率 ii) f,最后 iii) g 对输出进行排序。贪婪算法在此处的工作方式是,以度量的顺序选择交易,并且每当发生冲突时,都会重新调用 LP 求解器,但会删除对已添加交易和冲突交易的约束(对于所有已选择的交易,x_ixi 设置为 1,对于冲突交易,x_ixi 设置为 0)。重复此操作,直到区块已满。
Let B := {}
Let B_c:= {nil}
Let BS := 0
Let C := {}
while B_c != B:
B_c = LP.solve(sum(x.f), x.g <= BL, C)
Sort B_c by "heuristic"
for t in B_c:
if t has any conflict with tx in B:
C.add(x_t = 0)
break;
B.append(t)
C.add(x_t = 1)
return B
## Replace "heurestic" by f/g for standard,
f for high-value
## Sorting is in descending order我们将这些交易标记为 CGI-f/g 和 CGI-f。由于运行该算法的时间可能比其他贪婪算法更长,因此我们仅分析“全部”冲突。
模拟
由于我们处理该项目的时间有限,因此我们尝试合成地复制交易数据,而不是使用实际交易。为了正确地模拟以太坊 mempool 交易,我们选择了以下数据集:
数据集
我们在此分配下选择 2000 个交易。
- 80%: SMALL: g ~ N(24k, 3k) f/g ~ N(16,4) - 这些低 gas 消耗的交易智能合约交互最少,因此使用更少的 gas。在几乎所有情况下,这些交易的 gas 费都很小,因为它们通常不是优先级交易。
- 18% : LARGE1: g ~ N(200k, 20K) f/g ~ N(16,4) - 这些表示具有重要合约执行的交易。但是,在这种情况下,这些仍然不是优先级交易,因为用户可以等待一段时间才能执行合约。
- 2% : LARGE2: g ~ N(200k, 20K) f/g ~ N(40,10) - 这些是优先级交易。通常,这些交易具有很高的 gas 使用率,因为它们主要与 DeFi 合约交互,并且希望尽快执行。
我们通过随机选择交易来模拟这些交易之间的冲突,以使每个交易具有 \sigmaσ 个冲突。虽然我们的初步结果在所有类型的交易中都构成相同的 \sigmaσ,但实际上,较大的交易,尤其是高收益的交易,将具有更多冲突,因为通常会围绕它们构建提取 MEV 的捆绑包。
结果
我们对以上述方式创建的 mempool 中的 100 个区块进行了模拟。
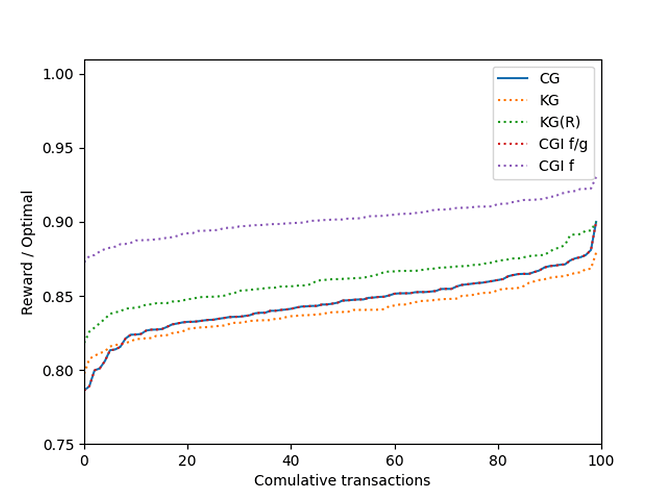
当我们考虑每个交易 \sigma=2σ=2 个冲突数时,我们看到以下结果:
每个交易的冲突数量的增加增加了问题的难度。因此,各种贪婪算法在性能上具有更大的分离度:
对于 \sigma = 10σ=10,
对于 \sigma = 20σ=20,
对于 \sigma = 40σ=40,
未来的研究方向
根据我们的结果,解决区块构建问题是一个 NP-Hard 问题,并且只要交易之间存在冲突,它仍然是一个复杂的问题。
但是,这并不意味着所有希望都破灭了。区块构建问题可能比最大独立集问题具有更大的潜力。将背包问题和最大独立集的空间结合在一起,可以为手头的问题找到令人满意的近似解决方案,从而缩小了搜索空间。
此外,对于搜索者的以太坊捆绑包,如果 tx_itxi 和 tx_jtxj 发生冲突,并且 tx_jtxj 和 tx_ktxk 发生冲突,则 tx_itxi 和 tx_ktxk 也极有可能发生冲突。由于在所有 2 个交易的图中,对于 MIS,你只需要选择效用最高的交易(也满足背包问题),因此这简化了对解决方案的约束。
另一要注意的是,我们的算法可以告知区块构建者如何在实践中构建区块。值得注意的是,经典贪婪信息算法(其中我们按最高费用对交易进行排序)最接近最佳解决方案。
话虽如此,对此研究最令人兴奋的扩展是将区块构建问题建模为作业排序问题,并以某种方式估计一个交易的效用(费用+MEV)如何影响在该交易之后排序的其他交易的效用。
在此说明,我们邀请潜在的合作者探索用于构建可最大化构建者效用的区块的新想法。
- 原文链接: ethresear.ch/t/block-bui...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 介绍 strawmap,一份由 EF 协议推出的概念路线图 90 浏览
- 深入探究 ENSv2 架构 95 浏览
- 什么是DeFi?去中心化金融指南 - CoW DAO 97 浏览
- L1 价值捕获的压缩 77 浏览
- 以太坊怎么了? 80 浏览
- DeFi和加密货币之间有区别吗?——CoW DAO 85 浏览
- 什么是DeFi聚合器?——CoW DAO 84 浏览
- 顶级DeFi交易所:理解去中心化交易基础设施 - CoW DAO 242 浏览
- 以太坊 2026年协议级更新确定 3 大方向 349 浏览
- 寻找底线:为什么我们为 Layer 2 构建了紧急提款出口( Exit Hatch) 235 浏览
- Solana的区块构建之战 264 浏览
- 如何去中心化构建区块? 325 浏览
 \
s2feeratio890×666 74.6 KB
\
s2feeratio890×666 74.6 KB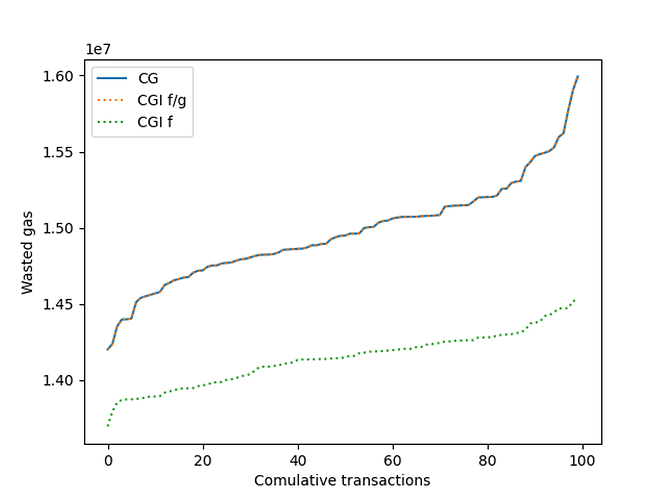 \
s2wastedgas890×666 56.3 KB
\
s2wastedgas890×666 56.3 KB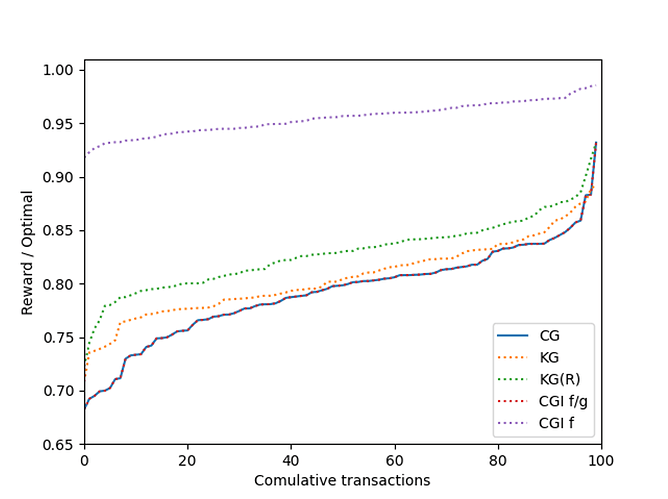 \
s10feeratio890×666 81.2 KB
\
s10feeratio890×666 81.2 KB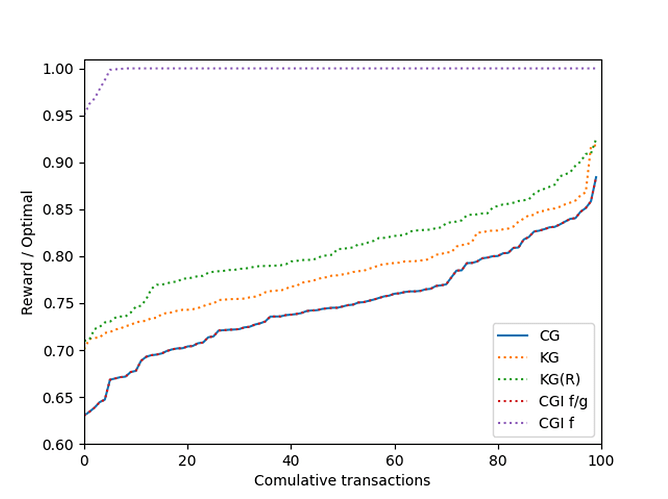 \
s20feeratio890×666 80 KB
\
s20feeratio890×666 80 KB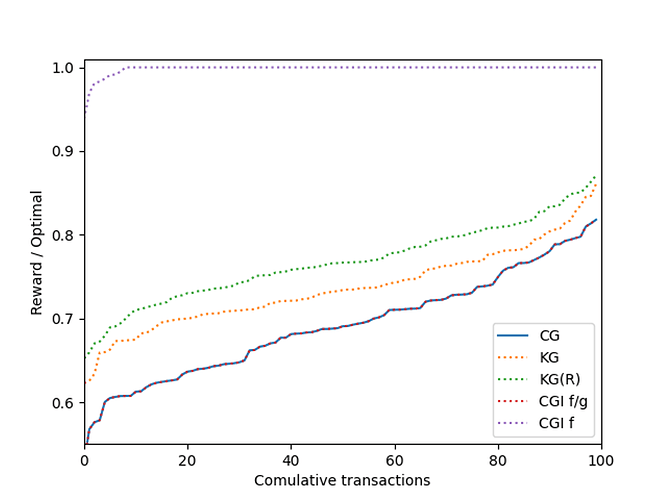 \
s40feeratio890×666 73.5 KB
\
s40feeratio890×666 73.5 KB
