具有圆形和螺旋最终性的Vorbit单Slot最终性:验证者选择和分配 - 权益证明
- 以太坊中文
- 发布于 2024-09-21 17:48
- 阅读 844
本文深入探讨了以太坊转向单Slot最终性(SSF)后的验证者管理和经济模型,提出了Vorbit方案,旨在通过快速轮换验证者委员会实现累积最终性。文章详细分析了Zipfian分布的验证者集合,以及在不同验证者整合水平和权益数量下,圆形和螺旋最终性对累积最终性的影响,并提出了优化辅助验证者选择和分配策略,以最小化aggregate finality gap。
_感谢 Francesco D’Amato 和 Barnabé Monnot 的反馈,以及 RIG + 朋友(1, 2)聚会的参与者,Orbit 的部分内容在此汇集——包括 Barnabé 的 finality stairwell。_
1. 简介
以太坊将过渡到 single-slot finality(SSF),以提供快速而强大的经济保证,保证包含在区块中的交易不会回滚。这需要升级共识算法(1, 2, 3, 4)和签名聚合方案(1, 2, 3),如 先前概述 的那样。第三个要求是升级以太坊的验证者经济学和管理,目前在 rotating participation 方面的进展已在 Orbit SSF 提案中提出。该领域的一些考虑因素包括如何激励验证者合并(1, 2),如何缓和权益数量(1, 2, 3, 4),以及如何选择活动集中的验证者。
有了 SSF,共识机制仍然由一个可用的链(例如,RLMD GHOST)和一个 finality gadget(例如,类似于 Casper FFG 或 Tendermint)组成。即使来自 EIP-7251 的验证者合并可以提供切实的改进,但所有验证者都能够参与每个插槽仍然是不太可能的。这意味着验证者必须被划分为委员会,每个委员会对可用链的头部进行投票和/或完成连续检查点。对可用链进行投票的委员会必须 rotate slowly,但这种严格的要求不适用于 finality gadget(在验证者完成其检查点之后)。
这篇文章将更仔细地研究当 finality 委员会快速或适度轮换时的累积 finality,提出验证者选择和分配的策略。即将发表的文章旨在审查较慢的验证者轮换的动态,重点是可用的链。为了正确地建模合并的影响,首先在 第 2 节 中给出了为特定数量的权益生成“纯 Zipfian”分布的方程,并以不同纯度级别生成了建模的 staking sets。然后在 第 3 节 中提出了一种在新类型的“epoch”中生成委员会的方法,并在不同的验证者合并和权益数量级别下分析了累积 finality——应用了各种委员会选择标准。一个好的评估指标是“aggregate finality gap”,它统计了一个区块在达到完全 finality 过程中的缺失 finality。事实证明,验证者的活动率不应该严格地由其大小决定。理想情况下,它会随着权益的数量和验证者集的组成而变化,因此称为“Vorbit”,表示可变的 Orbit。
当委员会被打乱时,累积 finality 会在 epoch 边界受到阻碍。因此,在 第 4 节 中提出了 circular finality,其中连续的 epoch 在更长的时代中重复,这样 finality 以循环方式累积。还引入了一种以螺旋方式打乱验证者集的机制,以改善打乱边界的 finality。第 5 节 分析了各种选择和分配方法的影响,并在 第 6 节 中展示了对 deposited stake 的 finality 的影响。第 7 节 回顾了预测最佳验证委员会数量的方法,第 8 节 回顾了与共识形成和权益风险相关的特征。
2. 用于建模的 Zipfian staking sets
2.1 纯 Zipfian 分布
为了建模基于委员会的 SSF,有必要定义验证者集中预期的合并级别,包括一个实际的范围。这个想法是在这个范围内生成验证者集,然后探索如何将每个集合最佳地划分为委员会。优化标准与累积 finality 相关。在即将进行的研究中,一个可实现的合并级别也可以作为探索合并激励措施的健康界限。
Vitalik 回顾了以太坊 早期 的 stakers 分布,并 确定 它大致是 Zipfian 的。然后规定,在“纯” Zipfian 分布下,staking deposit 大小 D 和 stakers 数量 N 之间的关系为 D=32N\log_2{N}。生成“纯” Zipfian staking set 的一个简单过程是将 stakers 的余额分配为
\frac{32N}{1}, \frac{32N}{2}, ..., \frac{32N}{N}.
当 N 很大时(如本例中),相关的调和级数
1 + \frac{1}{2} + ... + \frac{1}{N}
接近 \ln(N)+\gamma,其中 \gamma 是Euler-马斯切罗尼常数,约为 0.577。那么权益的总量是
D = 32N(\ln(N)+\gamma),
这接近 Vitalik 的近似值。附录 A.1 表明,N 因此可以确定为
N = e^{ W \left( \frac{D}{32} e^\gamma \right) - \gamma},
其中 W 表示 Lambert W function。这些方程为给定任何特定的 D 生成一个纯 Zipfian staking set 提供了蓝图。首先将方程应用于 D 以确定 N,然后使用涉及 N 的调和级数来创建分布。相应的两行 Python 代码在 附录 A.1 中提供。
2.2 建模的验证者集
图 1 显示了以青色显示的 staker 余额的最终分布。紫色是第二个分布(“1/2 Zipfian”),它是通过移除一半的 stakers(在排序集中,从第二大 staker 开始,每隔一个 staker)并将移除的 ETH 重新分配给 32-ETH 验证者来创建的。这旨在捕捉这样一种情况,即许多较大的 stakers 维护 32-ETH 验证者。即使他们最终合并,它仍然可以代表在未来几年内随着合并的缓慢进行,“名义” staker 集大小的中间分布。这篇文章使用了几个这样的分布,包括 9/10 Zipfian 分布(移除每十个 staker)、4/5 Zipfian 分布和 2/3 Zipfian 分布。
图 1. 在 D= 30M ETH 下,用于此文章建模的 staker 集大小分布的对数-对数图。青色中的集合大小遵循“纯” Zipfian 分布,紫色中的集合大小移除每隔一个 staker,并将权益重新分配给 32-ETH 验证者。
在 D= 30M ETH stake 下,纯 Zipfian 分布的 N\approx79\,000。以太坊的节点数量很难估计;爬虫程序只能提供下限。但是,对于这种假设分布,节点数量似乎略低于 staker 集大小。紫色中的 1/2 Zipfian 分布的 N\approx481\,000。这被认为是通往合并验证者集的一个点;然而,尚不确定进展的速度。
通过让拥有超过 2048 ETH 的 stakers(不包括那些已经重新分配给 32-ETH 验证者的人)将其权益划分为最大允许大小(s_{\text{max}}=2048)的验证者,这些 staking sets 被转换为验证者集 \mathcal{V},从而捕捉到理想的结果。此过程中的最后两个验证者被设置为小于 2048 的相等大小。例如,拥有 5048 ETH 的 staker 将拥有大小为 {2048, 1500, 1500} 的验证者。
在 Zipfian 分布下,大多数 stakers 拥有的 ETH 少于 2048,因此对于纯 Zipfian 分布,这仅增加了约 9000 个验证者,对于 1/2 Zipfian 分布,则增加了约 5000 个验证者。对于 Zipfian staking set,附录 A.2 表明,相应的 Zipfian 验证者集大小 V=|\mathcal{V}| 可以非常精确地估计为
V = \frac{N}{64} \left(63+\ln(N/64) + 2\gamma \right).
验证者计数和总和在合并级别上的分布如图 2 所示。
图 2. 在五个建模的验证者集中,30M ETH stake 下的验证者计数和总和的分布。轴是对数比例的。
3. 委员会、累积 finality 和 aggregate finality gap
3.1 委员会的生成
将 \hat{V_a} 定义为活动验证者集大小 V_a 的理想上限。该协议可以允许(并且希望)V_a 增加到 \hat{V_a},但不超过此限制。这篇文章将 \hat{V_a}=31250 设置为当 100 万个验证者被分成 32 个委员会时的委员会大小(大约反映了当前的委员会大小)。在使客户端能够处理更大的委员会方面取得了一些进展,但是 finality gadget 可能与今天略有不同(例如,使网络承受两倍的签名负载)。因此,如果需要,也可以使用相同的框架对 较小的委员会,例如 \hat{V_a}=4096 进行建模。
让 C 表示一种新型“epoch”中委员会的数量,该“epoch”构成了验证者集的完整轮换。首先将验证者集分成 C 个不相交的常规委员会,确保 V/C<\hat{V_a}。例如,D= 30M ETH 下的 4/5 Zipfian staking set 由大约 233000(k)个验证者组成。因此,一个 epoch 必须至少分成 C=8 个委员会,在这种情况下,每个常规委员会由大约 29100 个验证者组成。设置 C=8 留有在每个委员会中包含大约 V_{\mathrm{aux}}=\hat{V_a}-29\,100=2150 个 auxiliary 验证者的空间——这些验证者也已被分配参与其他常规委员会。一旦添加了这 2150 个验证者,最终的完整委员会将由 \hat{V_a} 验证者组成。
为了选择委员会的 auxiliary 验证者,大小为 s ETH 的每个验证者都会被分配一个权重 w。基线权重是
w(s)=\frac{s}{s_{\mathrm{max}}},
如前所述,其中 s_{\mathrm{max}}=2048。这类似于 Orbit SSF 的阈值操作,但它使用 s_{\text{max}} 而不是 1024。此更改区分了 1024-2048 范围内的验证者。Vorbit 在完全区分下表现最佳,并且此更改还使个人合并激励(在 第 8.3 节 中讨论)在 1024 以上合理。第 5.1 节 讨论了 Orbit 如何采用完全区分。大小为 s ETH 的验证者被抽选为下一个要包含在委员会中的 auxiliary 验证者的概率 P(s) 由下式给出:
P(s) = \frac{w(s)}{\sum_{v \in \mathcal{V}_{¢}} w(s_v)},
其中 v 表示不在委员会中的互补集 \mathcal{V}_{¢} 中的每个验证者,s_v 是验证者 v 的大小。然后,最小的验证者将倾向于参与大约 1/C 的 slots,而较大的验证者会更频繁地参与,结果取决于权益的数量和合并级别(另请参见图 22)。
3.2 累积 finality
图 3 显示了 4/5 Zipfian staking set 的 stepwise 基于委员会的 累积 finality,其中委员会完成连续的 slots。对于包含在区块 n 中的交易,aggregate finality 在委员会投票的 slot 结束时进行视觉统计。仅使用常规委员会时的 finality 使用虚线蓝色表示。由于每个常规委员会完全不相交并按比例反映整体分布,因此每个委员会都会向未完成的交易/区块添加相等的边际累积 finality。图 3 中的实线蓝色显示了当示例中的每个常规委员会都已由 auxiliary 验证者补充到 \hat{V_a} 时(“Full”)的累积完成。
图 3. 4/5 Zipfian staking set 的区块 n 的累积完成。finality gap(蓝色箭头)逐渐减小。aggregate finality gap 是所有 finality gaps 的总和,直到完全 finality(青色区域)。
3.3 Aggregate finality gap
让 D_f 表示已完成区块的 stake 的数量,D 表示为 staking deposit 的 stake 总量。finality gap F_g 是尚未完成区块的 stake 的比例:
F_g = \frac{D-D_f}{D}.
虽然 D_f 是单独衡量经济安全性的相关指标,但如果 D 未知,则 D-D_f 的用处较小。只要新的验证者参与到完成的委员会中,区块的 finality gap 就会随着每个新 slot 而下降。具有完整委员会的示例具有较低 的finality gap,这是由于 auxiliary 验证者提供的额外 finality 造成的。由于它们是以加权方式选择的,因此即使在此示例中仅添加了大约 2150 个额外的验证者,效果也非常明显。随着完全 finality 的临近,finality gap 的差异会减小。在这一点上,大多数验证者无论如何都将作为其常规分配的一部分出现,并且在这种比较中,重复验证者不会改善 finality(当重复验证者时,可能会提出更高的经济安全性的论点,但这超出了本文的范围)。
在处理累积 finality 时,一个有用的实用指标是区块在共识形成期间直到完全 finality 所承受的 aggregate finality gap \widetilde{F}_{\!g}。它由图 3 中的青色区域表示,并计算为
\widetilde{F}_{\!g} = C - \sum_{i=1}^{C} F_{g}(i).
3.4 Auxiliary 委员会
如果将 4/5 Zipfian set 分成 9 个委员会而不是 8 个,会发生什么?添加的 auxiliary 委员会 (C_{\mathrm{aux}}=1) 会导致每个委员会中包含 \hat{V_a}/9\approx3470 个 auxiliary 验证者,从而进一步减少 \widetilde{F}_{\!g}。图 4 显示了 8 个委员会(蓝色)和 9 个委员会(紫色)的 epoch 之间的比较。区块 n 的 finality gap 差 \Delta F_{\!g} 用绿色表示 gap 减少的 slots,用红色表示 gap 增加的 slots。累积 finality 首先会得到改善,这是由于额外的 auxiliary 验证者,并且这是最明显的效果。随着重复验证者的数量增加,减少的效果会减小。在 slot n+7 开始时,分为 8 个委员会的验证者集反而具有较低的 F_g,并且它会在一个 slot 之前,在 slot n+8 开始时达到完全 finality。
图 4. 4/5 Zipfian staking set 的区块 n 的累积完成。当添加 auxiliary 委员会时,每个委员会中有更多空间容纳具有高余额的 auxiliary 验证者(紫色线),因此 finality 在初始阶段积累得更快。
如图 5 所示,当添加更多的 auxiliary 委员会时,aggregate finality gap 继续下降。在 C_{\mathrm{aux}}=3 和 C_{\mathrm{aux}}=4 之间的比较中,\Delta F_{g} 从 slot n+5 开始变为负数,并一直下降到 slot n+12。因此,对于这两种配置,aggregate finality gap \widetilde{F}_{\!g} 大致相等。
图 5. 4/5 Zipfian staking set 的区块 n 的累积完成,比较了不同数量的 auxiliary 委员会之间的结果。
图 6 显示了纯 Zipfian staking set 的相同示例。在 C_{\mathrm{aux}}=4 时,几乎 20M ETH(2/3 的 stake)将在第一个 slot 中完成该区块。与之前的示例一样,添加 auxiliary 委员会的好处会随着添加的越多而减少(\widetilde{F}_{\!g} 停止下降并最终反转)。
图 6. 纯 Zipfian staking set 的区块 n 的累积完成,比较了不同数量的 auxiliary 委员会之间的结果。
图 7 显示了 1/2 Zipfian staking set 的结果。大约 48.6 万个验证者需要至少分为
\left\lceil \frac{486000}{\hat{V}_{\!a}} \right\rceil = 16
个委员会。在没有完整委员会的情况下,每一轮只有 187.5 万 ETH 会完成。这似乎存在问题,因为未能完成的委员会将 阻止 finality,直到委员会中有足够数量的 stake 通过非活动泄漏或类似机制被替换。在这种情况下,可以考虑加速非活动泄漏。但是,从问责制的角度来看,这种级别的 stake 已被认为 完全足够 。
图 7. 1/2 Zipfian staking set 的区块 n 的累积完成,比较了不同数量的 auxiliary 委员会之间的结果。
4. Circular 和 spiral finality
前一小节中的图都捕获了一个 epoch 的累积 finality,并且代表了一个 epoch 中第一个区块。在每个 epoch 中,都会迭代整个验证者集,因此在 epoch 结束时会达到完全 finality。但是,如果在 epoch 之间打乱验证者集,则只有 epoch 中的第一个区块才能在 epoch 结束时达到完全 finality。对于 epoch 中稍后 slots 的区块,直到下一个 epoch 结束时才能达到完全 finality。边际累积 finality 在 epoch 边界处显着降低,因为边界两侧的委员会将具有更多的验证者重叠(即使仅使用常规委员会)。因此,当声明 4/5 Zipfian staking set 可以在八个 slots 内达到完全 finality 时(如图 3-5 所示),这是一个有条件的声明。对于 epoch 的第二个区块,直到 15 个 slots 之后才能达到完全 finality(第一个 epoch 中的 7 个 slots 和后续 epoch 中的 8 个 slots)。回想一下,C 表示一个 epoch 中委员会的数量,因此也是常规操作期间一个 epoch 中 slots 的数量。那么达到完全 finality 的平均 slots 数 \bar{S}_{\!f} 变为
\bar{S}_{\!f}=C + \frac{C-1}{2}.
虽然完全 finality 可能更多的是一种概念上的担忧,但如果区块是在 epoch 的最后一个 slot 中提出的,那么从打乱开始的性能下降已经在第二个 slot/委员会中开始了。有两种方法可以改进这一点:circular finality 和 spiral finality。两者都从区块的第二个积累 finality 的 slot 开始提供好处。
4.1 Circular finality
最简单的解决方案是避免每个 epoch 都打乱验证者集。相反,验证者集是在 era 中打乱的,每个 era 可以由多个 epoch 组成。每个 era 的 epoch 数 E_{\text{era}} 由每个 era 所需的 slots 数 \hat{S}_{\text{era}} 和 C 确定,四舍五入到最接近的整数:
E_{\text{era}}=\lfloor\hat{S}_{\text{era}}/C\rceil.
通过此更改,era 的前 (E_{\text{era}}-1)C 个区块将在 C 个 slots 中完成,而最后 C 个区块将按照先前的等式 C + (C-1)/2 完成。此外,也许更重要的是,在 era 内跨越 epoch 边界时,累积 finality 不会降低。在 era 的 E_{\text{era}}\times C 个区块中,达到完全 finality 的平均 slots 数变为:
\bar{S}_{\!f}=\frac{C(E_{\text{era}}-1)C + C(C + (C-1)/2)}{E_{\text{era}}\times C},
简化为
\bar{S}_{\!f}=C + \frac{C-1}{2E_{\text{era}}}.
例如,设置 \hat{S}_{\text{era}}=64。没有 auxiliary slots 的 4/5 Zipfian staking set 将在 8 个 slots 中完成 64 个区块中的 57 个,剩余的每个区块分别在 9、10、11 个 slots 中完成,等等。此外,era 中只有最后 7 个 slots 中的 64 个会受到累积完成的降低,而如果没有 circular finality,则 64 个 slots 中的 56 个会受到影响。达到完全 finality 的平均 slots 数变为 \bar{S}_{\!f} \approx 8.4。相比之下,如果没有 circular finality,则结果为 \bar{S}_{\!f}=C+(C-1)/2 = 11.5。
4.2 Spiral finality
虽然 circular finality 在降低 \bar{S}_{\!f} 和降低具有降低累积 finality 的区块比例方面有效,但它不会降低达到完全 finality 的最大时间,该时间仍然为 S_{f} = 2C-1。此最大值适用于在 era 的最后一个 epoch 的第二个 slot 中提出的区块。一种减少此最大值的方法是 spiral finality,其中对验证者在被打乱时在 epoch 内可以向前移动多少个 slots 进行了限制。这由变量 C_{\text{shift}} 控制。设置 C_{\text{shift}}=2 意味着验证者只能向前移动两个 slots,但他们始终可以移回 epoch 的开头。然后,可以将 epoch \mathcal{C}_n 的第一个委员会中的常规验证者重新分配到委员会 \mathcal{C}_n 和 \mathcal{C}_{n+2} 之间,可以将委员会 \mathcal{C}_{n+1} 中的常规验证者重新分配到委员会 \mathcal{C}_n 和 \mathcal{C}_{n+3} 之间,等等。如果 \hat{V}_a 设置得相对较低,则可能需要对随机选择进行进一步的规定,以确保大小验证者的均匀分布。
可以将 cicular 和 spiral finality 组合起来,以实现较低的达到完全 finality 的平均时间,以及较低的上限。在此设置中,spiral finality 应用于 era 的最后一个 epoch。
5. 优化 auxiliary 验证者的选择和分配
本节回顾了两种不同的优化 auxiliary 验证者分配的方法。与以前一样,这些图将忽略 epoch 边界(假定 circular finality)。实际上,为了根据验证者选择过程中固有的随机性提供更稳定的结果,在本文中,所有累积 finality 图中都以循环方式评估 finality。这涉及计算所有 C 个不同起始位置的 C 个连续 slots 的结果。此外,该方法可确保验证者的间隔和分布与 epoch 边界不一致,并且在 [第 5.2 节](https://ethresear### 5.1 调整权重
最直接的修改是通过将幂 p 添加到原始等式来调整权重方案:
w(s)=\Big(\frac{s}{s_{\mathrm{max}}}\Big)^p.
如果 p>1,则较大的辅助验证器将比较小的验证器获得更高的优先级。这可能很有用,因为仍然保证较小的验证器包含在一个委员会中,并且 C 可以相对较小(短 epoch)。 当直接从权重中选择验证器,并且没有常规委员会时,Orbit 慢旋转范例的一个潜在变化是,p 可以设置为低于 1。这降低了阈值机制的“斜率”,允许以高于例如 1/32 或 1/64 的概率选择较小的验证器。 这可能对第 8.3 节中讨论的原因有利,并且将在涵盖慢速旋转验证器集的帖子中进一步探讨。
图 8 显示了当将 p 从 1 更改为 2 时,最终确定权益 \Delta D_{f} 方面的最终确定性差距的差异。 使用了五个验证器集(从 1/2 Zipfian 到完全 Zipfian)的平均结果。 读者可能还希望查看第 8.2 节中的图 22,该图显示了权重变化如何改变大小为 s 的验证器处于活跃状态的概率。
图 8. 在区块进展到完全最终确定性期间,当 p 从 1 更改为 2 时,30M 权益时的 D_{f} 变化。
显而易见的是,当 C_{\text{aux}} 在 3-4 之间时(这些线在图中有些重叠),第一个Slot的 D_{f} 平均高出近 5M ETH。 这是一个显着的改进,将第一个Slot的最终确定性差距减少了近 1/6。 然后,具有 2-4 个辅助委员会的示例从 n+5 开始略有减少。 这是因为具有最多权益的验证器几乎包含在每个委员会中:重复的验证器不会增加累积最终性,并且它们占据委员会中的空间,从而阻止新的验证器最终确定该区块。
5.2 相等间距
由于重复的验证器不会增加累积最终性,因此最好在整个 epoch 中平均间隔重复的辅助验证器,以便重复尽可能地分开进行。 然后可以稍微不同地进行辅助验证器的分配。 可以为权益为 s 的验证器设置辅助包含的数量 \lambda,如下所示
\lambda(s) = \frac{V_{\text{aux}}(C-1)w(s)-\widetilde{V}_{\!\text{aux}}}{\sum_{v \in \mathcal{V}} w(s_v)}.
在该等式中,\widetilde{V}_{\!\text{aux}} 对存在于每个Slot中的验证器在整个 epoch 中添加的辅助验证器实例求和。 它最初设置为零。 对于任何 \lambda_v > C-1 的验证器 v,迭代过程设置 \lambda_v = C-1,从 \mathcal{V} 中删除该验证器,将 C-1 添加到 \widetilde{V}_{\!\text{aux}},并重新计算其余验证器的 \lambda。 依赖于 \widetilde{V}_{\!\text{aux}} 的迭代过程是必要的,因为一个验证器在一个Slot中永远不能包含超过一次(\lambda \not > C)。
给定 \lambda,每个验证器都保证包含在 \lfloor \lambda \rfloor 个委员会中,剩余的任何分数都将在绘制将包含在一个额外的辅助委员会中的验证器时使用。 最终结果表示为 \lambda_f。 验证器的辅助包含以 C/(\lambda_f+1) 个Slot的间隔均匀间隔。 间隔过程从常规委员会位置开始,将计算出的距离四舍五入到最接近的整数,并使用模运算环绕 epoch 边界。
由于验证器分配中的随机性,使用此过程的Slot通常会略低于或高于 \hat{V}_a。 一般来说,这不应该是一个问题,因为 \hat{V}_a 通常会允许一些灵活性。 但是,为了与评估中的随机抽取保持一致,迭代过程将验证器从具有超过 \hat{V}_a 个验证器的委员会重新分配给验证器数量较少的委员会,仍然确保委员会内没有验证器重复。
令 \equiv 表示相等间距,\not\equiv 表示由于随机抽取而实现的间距。 在权益为 30M ETH 时的变化 \Delta D_f,计算为 D_f(\equiv) - D_f(\not\equiv),如图 9 所示。 变量 p 对于随机和等间距的验证器都设置为 2。
相等间距带来的最显着改进发生在区块提出后的第二个Slot中。 按照定义,第一个Slot无论如何都不会包含任何重复。 当辅助委员会较少时,改进最为明显,因为在这些情况下,2048-ETH 验证器几乎不包含在每个委员会中。
图 9. 在区块进展到完全最终确定性期间,当验证器在整个 epoch 中等间距时,权益为 30M 时的 D_{f} 变化。
使用 p=2 和相等间距的 4/5 Zipfian 权益集的outcome如图 10 所示。 它可以与图 5 中的上一个图进行比较,该图显示了 p=1 和随机间距的结果。 这些变化在 C_{\text{aux}} 为 3-4 时将第一个Slot的 D_f 从 15M ETH 增加到 20M ETH,在 C_{\text{aux}}=1 时将第二个Slot的 D_f 从 15M ETH 增加到 20M ETH。
图 10. 具有 p=2 和相等间距 \equiv 的 4/5 Zipfian 权益集区块 n 的累积最终确定性。
6. 跨 D 的分析
本节和下一节中的分析依赖于 p=2 和辅助验证器的随机分配 \not\equiv。 图 11 显示了对于 4/5 Zipfian 集,聚合最终确定性差距如何随 C_{\text{aux}} 在存款大小上变化。 在较低的权益数量下,C_{\text{aux}}=0 给出最低的 \widetilde{F}_{\!g}。 在较高的权益数量下,C_{\text{aux}}=5 给出所绘制的最低值。 但是,将 C_{\text{aux}} 一直增加到 7 将错误地给出高于 70M ETH 的最低结果。 但是,在更高的设置下,结果非常紧密地重叠(因此未绘制),这意味着就 \widetilde{F}_ {\! g} 而言,冒险高于 C_{\text{aux}}=4 不会带来显着的改进。
当由于 C 的变化而重新分配验证器时,会出现Characteristic shark fin-pattern。 随着 D 增加而分布保持固定,V 也增加。 每个“鳍”代表添加一个委员会。 此添加为更多辅助验证器提供了空间,当 C_{\text{aux}} 相对较低时,这会减少 \widetilde{F}_ {\! g}。 但是,如果对于给定的验证器集而言 C_{\text{aux}} 太高,则结果会反转,并且添加一个委员会反而会增加 \widetilde{F}_ {\! g}。 这在图 12 中很明显,图 12 放大了 D= 35M ETH 以下的结果。
图 11. 各种辅助委员会数量的 4/5 Zipfian 集在 D 上的聚合最终确定性差距。
图 12. 各种辅助委员会数量的 D\leq 35M ETH 的 4/5 Zipfian 集的聚合最终确定性差距。
将 \widetilde{F}^*_{\!g} 定义为在关联的最小辅助委员会 C^_{\text{aux}} 处实现的最小聚合最终确定性差距。 这对应于图 11-12 中任何特定 D 处的最低线。 图 13 绘制了所有五个权益集的 \widetilde{F}^ * _ {\!g}。 显而易见的是,有两种基本因素会降低基于委员会的累积最终确定性:更高的权益数量和更低的整合水平。
图 13. 跨权益的最小聚合最终确定性差距。 更高的权益数量和更低的整合水平都会降低快速最终确定性。
图 14 而是侧重于 \widetilde{F}^*_{\!g} 处的最佳委员会数量如何变化。 但是,最佳委员会数量会由于图 12 中明显的类鳍状模式而大大波动,并且它也是一个离散的度量。 因此,将抛物线插值(参见附录 B.3)应用于最小值周围的三个点,从而获得更平滑的总委员会表示,此处表示为 C^y。 随着权益数量的增加,聚合最终确定性差距和委员会总数都呈线性上升,保持分布固定。
图 14. 最大程度地减少聚合最终确定性差距的插值总委员会数量。
7. 预测最佳辅助委员会数量
7.1 概述
如果采用所建议的基于委员会的最终确定性变体,则应如何在运营期间确定辅助委员会的数量(或任何其他设置,例如 p)? 可以高亮显示五个选项:
- 生成委员会并计算 \widetilde{F}_ {\! g}(或一些更合适的度量,如附录 B.2中进一步讨论的那样),用于各种 C_{\text{aux}} 设置(例如,0-6),选择最小化 \widetilde{F}_ {\! g} 的设置。 如果有数十万个验证器,则此解决方案可能具有很高的计算负载。
- 仅为当前和相邻的 C_{\text{aux}} 设置运行该过程。 如果频繁执行分析,请存储结果并依靠滞后,仅当最近的大多数评估都赞成时才进行切换。 例如,可以使用过去一周的 80% 的阈值。
- 如果 (2) 中的计算负载仍然太高,则可以依靠缩减的验证器集 \mathcal{V}_ r,其中 \mathcal{V}_ r 中的验证器从有序的完整集 \mathcal{V} 中平均间隔抽取。 然后,应将 \hat{V_a} 的设置降低到与生成委员会之前验证器集减少成比例的程度。
- 计算与验证器集的一些简单特征,例如可变性,并基于这些特征确定适当数量的辅助Slot。
- 指定固定数量的辅助委员会,以便该机制在各种验证器集下表现良好,例如 C_{\text{aux}}=2。
在实施复杂性方面,所有选项都相当简单。 选项 1-3 的一个好处是客户端无论如何都需要实施将验证器分配给委员会的功能。 剩余的过程是附录 B.1中描述的评估函数。 此过程没有很高的时间复杂性,但如果有很多数十万个验证器,则它可能仍然在计算上过于密集。
然后,选项 2 相当有吸引力,与更新验证器的有效余额时如何利用滞后效应有一些相似之处。 选项 3 可以通过至少一个数量级 (10x),甚至最多两个 (100x) 来进一步降低计算要求。 然后一个问题是,如果验证器集减少到例如 |\mathcal{V}_ r| = 1000 或 |\mathcal{V}_ r| = 5000,则可以达到什么样的准确度。 第 7.2 节对此进行了研究。 当然,另一个问题是选项 4 的可行性,这可以进一步降低计算要求。 第 7.3 节对此进行了研究,并且在第 7.4 节审查了选项 5。 实验的结论在第 9 节中进行了扩展,即选项 2、3 或 5 似乎是最可行的,选项 5 是一个自然的起点。
用于建模的基本事实不是基于最佳辅助委员会数量 C_{\text{aux}},而是基于最佳辅助验证器数量 V_{\text{aux}},主要是为了规避图 11-12 中的类鳍状模式。 为了获得更平滑的目标,通过抛物线插值导出了相邻 V_{\text{aux}} 值之间的更精细点 V^{y}_{\text{aux}},如先前在图 14 中也针对 C^y 所示。 在插值之前进行了进一步的小调整,当应用相对于常规Slot数量的大量辅助Slot时,略微加权 \widetilde{F}_ {\! g}。 附录 B.2-3 解释了生成基本事实的完整过程。 附录 B.4 然后描述了生成额外的对数正态验证器集,以在评估的示例中提供更大的分布。 它在图 15-20 中以黄色显示。 为分析的六种不同分布中的每一种生成了一千个验证器集,D 的范围为 10M-80M ETH,总共给出了 6000 个示例。
7.2 使用缩减的验证器集进行预测准确性
如果 \mathcal{V}_r 仅包含 1000 或 5000 个验证器,则使用选项 3 中的缩减的验证器集 \mathcal{V}_r 可以获得多大的预测精度? 为了测试这一点,使用与在完整集上设置基本事实 V^{y}_{\text{aux}} 时相同的评估过程,在缩减的集上计算了预测的最佳值 V^{x}_{\text{aux}}(附录 B.1)。 结果如图 15 所示,对于 1000 个验证器(R^2=0.893),图 16 所示,对于 5000 个验证器(R^2=0.960)。 较宽的黑色对角线代表完美的预测,而较细的黑线表示预测落在 \hat{V}_{\!a} 范围内的范围。
图 15. 基于 1000 个验证器的缩减集,预测的最佳辅助验证器数量与基本事实相比。
图 16. 基于 5000 个验证器的缩减集,预测的最佳辅助验证器数量与基本事实相比。
显而易见的是,对于 V_{\text{aux}} 的较高值,预测变得越来越不准确。 这与图 11 中显示的现象有关,其中 \widetilde{F}_{\! g} 的相对差异在 C_{\text{aux}}(因此 V_{\text{aux}})的最佳设置之间不会那么大。 更广泛的含义是,C_\text{aux} 稍微错误不会有太大关系。 在另一方面,在左下角较低的 C_\text{aux} 处出错更令人担忧。 另请注意,只有 D> 40M ETH 的示例才有问题(查看图 20,了解基本事实范围 25M-35M)。
预测中的错误源于随机选择如何影响委员会的组成。 因此,重复该实验几次并平均结果将有助于提高准确性(如第 5.2 节中描述的等间距验证器)。 图 17 显示了 V_{r} = {1000, 2000, 3000, 5000} 的四个验证器集的平均结果的示例。 现在,所有预测都在 \hat{V}_a 边界内,并且 R^2=0.981。 还必须记住,虽然 V^{y}_{\text{aux}} 按照定义是基本事实的理想结果,但它本身也会反映在生成过程中验证器的随机划分。
图 17. 基于四个缩减集的平均值,预测的最佳辅助验证器数量与基本事实相比。
7.3 使用一般特征进行预测准确性
是否可以使用一般特征来确定最佳辅助验证器数量? 为了探讨这一点,为模拟的验证器集生成了特征,捕获了基本属性,例如验证器计数、存款大小以及各种可变性度量。 使用 2 次多项式特征扩展来生成原始特征的所有单项式,捕获交互和非线性关系。 然后使用多元线性回归进行预测。 通过半自动正向特征选择过程选择最终特征,手动选择顶级预测器中的预测器,以使那些更容易解释的预测器成为主要预测器(关键要求是一个简单的模型)。 此过程生成了一个由三个特征组成的线性回归模型:{V\sigma, V_w\delta, D^2}。
第一个特征是验证器数量 V 乘以验证器集的标准偏差 \sigma。 如果标准偏差很高,则辅助验证器对于减少最终确定性差距特别有用。 第二个特征将平均绝对偏差(表示为 \delta)乘以验证器的加权计数 V_w。 权重为 32 和 2048 的验证器分配权重为 1,然后在平均验证器大小 \bar{\mathcal{V}} 处,权重以对数线性方式降至 0。 具体来说,每个持有 s ETH 的验证器都会收到以下权重:
\text{加权计数}(s) = \begin{cases} 1 - \frac{\log(s) - \log(32)}{\log(\bar{\mathcal{V}}) - \log(32)} & \text{如果 } s \leq s_1 \\ 1 - \frac{\log(2048) - \log(s)}{\log(2048) - \log(\bar{\mathcal{V}})} & \text{如果 } s > s_1 \end{cases}.
V^{x}_{\text{aux}}<0 的预测设置为 0(辅助验证器的数量不能为负)。 预测的 R^2=0.975,如图 18 所示。 较低的左下角的更宽分散有些成问题,如前所述。 因此,选项 4 的结果比选项 3 稍微差一些。 另请注意,由于没有训练/测试拆分,因此可以假定存在相当多的过度拟合。 如果要认真地追求选项 4,则需要有一个测试集以及更多种类的训练示例。
图 18. 基于捕获一般特征的最佳辅助验证器数量与基本事实相比,例如,验证器集中的可变性。
7.4 使用固定数量的辅助委员会进行预测准确性
审查具有固定数量的辅助委员会的结果也可能很有趣。 将所有示例设置为固定 C_{\text{aux}}=2 时的结果如图 19 所示。 它在 \hat{V}_a 宽的垂直带中生成预测,与基本事实的偏差远远超出 \hat{V}_a。 图 20 而是侧重于 25-35M ETH 的范围。 在这种情况下,预测倾向于落在 \hat{V}_a 范围内,除了对数正态分布,该分布有几个示例,其中验证器余额几乎没有或没有可变性(在这种情况下,辅助Slot没有任何好处)。 这说明,如果 D 保持在较窄的范围内,则最佳辅助委员会/验证器的数量变化会大大减少。 因此,从固定数量的辅助委员会开始是一种可行的基准策略。
图 19. 具有固定 C_{\text{aux}}=2 的最佳辅助验证器数量与基本事实相比。
图 20. 对于范围 D= 25M-35M ETH 中的验证器集,具有固定 C_{\text{aux}}=2 的最佳辅助验证器数量与基本事实相比。
8. 与共识形成相关的属性
8.1 委员会轮换率
将委员会轮换率 R 定义为在最终确定后连续的委员会中替换的权益比例。 如果所有验证器都被替换,则 R=1;如果所有验证器都保留,则 R=0。 图 21 显示了在权益为 30M ETH 时,R 如何随 V_{\text{aux}} 变化。 除了与可用链的慢速轮换机制相关之外,先前还讨论了讨论用于利用 Casper FFG 的最终确定性小工具的上限。 该建议 R=0.25 用黑色水平线表示。 圆圈表示聚合最终确定性差距最小化的点 (V^*_{\text{aux}})。 这发生在相当适度的轮换率下,当然可以很容易地进行调整。 添加约 150k 辅助验证器实例(C_{\text{aux}}\approx5)后,轮换变得相对较慢,其中每次委员会最终确定和轮换时,90% 的权益都保留不变。
图 21. 辅助验证器之间的委员会轮换率 R。 圆圈表示聚合最终确定性差距最小化的点。
8.2 活动率
活动率 a 捕获验证器处于活动状态的委员会比例(在 Orbit 帖子中定义为 p)。 倒数 a^{-1} 捕获验证器参与其中一个委员会之前的平均Slot数,并将被称为验证器的“远点”——其轨道距离。
图 22 显示了当聚合最终确定性差距最小时(在图 21 中用圆圈标记的 V^*_{\text{aux}} 处),a 如何随验证器大小 s 变化。 显而易见的是,a(s) 不是跨验证器集的固定属性,并且会随整合水平和存款大小等因素变化。 利用可变轨道(“Vorbit”)似乎很自然,因为以太坊希望优化的众多特征会随验证器集的组成而变化(先前也提出了一个动态阈值)。
[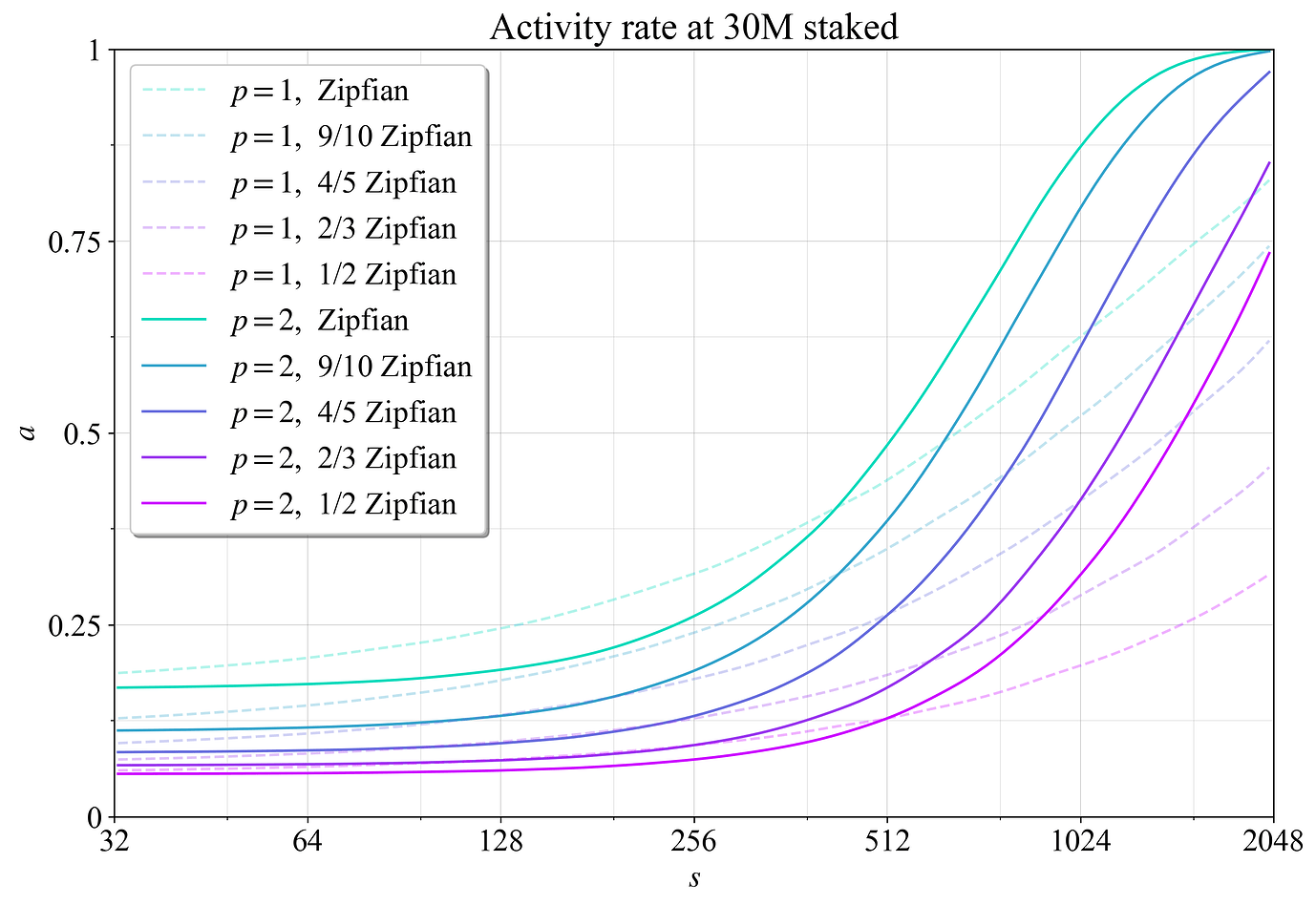 \
图 222641×1816 420 KB](https://ethresear.ch/uploads/default/original/3X/c/a活动比率 a_r = a(s_{\mathrm{min}})/a(s_{\mathrm{max}}) 捕捉了余额较小的验证者相对于余额较大的验证者活跃的频率。近拱点比率再次表示倒数 a^{-1}_r,有时可能更容易解释:a^{-1}_r=32 意味着小型验证者出现的频率比大型验证者低 32 倍。当 a_r 较小(因此 a^{-1}_r 较大)时,运行余额接近 s_{\mathrm{min}} 的验证者的质押者将比运行余额接近 s_{\mathrm{max}} 的验证者的质押者承担更低的惩罚风险。不活跃的验证者很难(错误或其他原因)做出可被惩罚的行为。因此,运行许多小型验证器的人可以及早发现错误的设置,从而使受影响的验证器比例更小。同样,小型验证器不太可能卷入一场灾难性的惩罚事件。即使这样的事件每 100 年才发生一次,它仍然会严重影响质押的预期价值,特别是如果未来总质押收益率下降的话。
\
图 222641×1816 420 KB](https://ethresear.ch/uploads/default/original/3X/c/a活动比率 a_r = a(s_{\mathrm{min}})/a(s_{\mathrm{max}}) 捕捉了余额较小的验证者相对于余额较大的验证者活跃的频率。近拱点比率再次表示倒数 a^{-1}_r,有时可能更容易解释:a^{-1}_r=32 意味着小型验证者出现的频率比大型验证者低 32 倍。当 a_r 较小(因此 a^{-1}_r 较大)时,运行余额接近 s_{\mathrm{min}} 的验证者的质押者将比运行余额接近 s_{\mathrm{max}} 的验证者的质押者承担更低的惩罚风险。不活跃的验证者很难(错误或其他原因)做出可被惩罚的行为。因此,运行许多小型验证器的人可以及早发现错误的设置,从而使受影响的验证器比例更小。同样,小型验证器不太可能卷入一场灾难性的惩罚事件。即使这样的事件每 100 年才发生一次,它仍然会严重影响质押的预期价值,特别是如果未来总质押收益率下降的话。
在慢速轮换机制中,鉴于验证者具有较高平均近拱点的质押者可以有更多时间来(例如)调整不活跃验证者的错误设置,然后再恢复活跃状态,因此 a_r 尤其重要。然而,a_r 在快速轮换机制中也相关。为了鼓励合并,相对于小型验证者,大型验证者承担了额外的风险,个人激励应该对此进行补偿。个人激励也可能与集体合并激励相结合。当 a_r 较小时,个人激励通常需要更高,因为运行小型验证器的益处会增加。因此,应尽可能使 a_r 接近 1。这可以最大限度地减少小型验证器和大型验证器之间的收益差异,从而减少质押者之间的“紧张关系”。在高收益差异下,这种紧张关系会出现,在这种情况下,以太坊将偏爱(或至少看起来偏爱)拥有更多资本的质押者。
即使额外的收益旨在补偿增加的风险,只有拥有高资本的质押者才能选择较高和较低的风险。如果拥有更多资本的质押者决定拆分其质押,他们也将不成比例地受益于调整其众多验证器之一中的错误设置的能力。因此,如果大型质押服务提供商 (SSP) 依靠小型验证器来降低其风险状况,并且集体激励因此降低了所有人的收益,那么也可能会出现紧张关系。例如,可能会有人呼吁攻击特定 SSP 的验证器,从而给共识形成带来不健康的动态。这与在使用英式拍卖时可能出现在 MEV 销毁 中的问题类型相似,在这种情况下,SSP 需要通过提前的构建者出价来专门针对彼此,以保持竞争力。
在图 22 中,对于 p=2 的 Zipf 分布质押集,a_r 大约为 1/6。具有 2048 ETH 的验证器始终存在,而具有 32 ETH 的验证器仅作为 epoch 的 6 个委员会之一的常规验证器存在。通常,这种情况比最小的验证器仅每 32 个插槽出现一次更好,就像 Orbit 阈值机制一样。但是,可以通过设置 p<1 来调整 Orbit 阈值机制。在后续文章中,为了解决可用链的慢速轮换问题,计划进一步探索这种途径,以及超出本文范围的其他相关共识问题。
允许 1-ETH 验证器将进一步降低活动比率,从而需要增加收益差异。因此,较小的验证器余额(如 1 ETH)将需要进行沟通,以解释为什么这些验证器获得的收益明显较低,以及为什么不能阻止大型质押服务提供商依靠 1-ETH 验证器来降低其风险状况(但当然可以通过公共论述来朝着相反的方向推动)。
9. 结论与讨论
已经在快速轮换的验证器委员会下审查了累积委员会最终性。评估累积最终性的一个良好衡量标准是聚合最终性差距 \widetilde{F}_{\!g},它聚合了一个块在完成完整最终性的过程中所产生的最终性差距。减少(改善)\widetilde{F}_{\!g} 的四个主要途径是:
- 除了所有验证器在一个 epoch 中进行一次投票所需的委员会之外,再添加一些辅助委员会(大约 2-4 个),
- 将最大的验证器包含在几乎每个委员会中,
- 均匀地间隔辅助验证器以最大限度地减少连续重复,
- 追求“循环最终性”(在一个较长的时代重复 epoch)和“螺旋最终性”(约束洗牌)以减轻洗牌期间累积最终性的降级。
分析中使用了五个验证器集,捕捉了不同级别的 Zipfianness。第 6 节 明确表明,验证器合并不足和更高数量的质押(保持分布固定)都会阻碍最终性,从而增加 \widetilde{F}_{\!g}。在考虑减少质押量时,一种观点是它会产生更高数量的小型验证器。无论这种理论的优点如何,都应注意,如 Figure 13 所示,更高数量的质押和很大比例的小型验证器相结合会导致累积最终性的最差条件。
审查了动态调整辅助委员会数量的方法。最好的方法是简单地模拟和评估具有相同或一个更多/更少辅助委员会的结果。如有必要,可以在简化的验证器集上执行此操作以提高性能。但是,辅助插槽的数量是否应动态更改并不是一个严格的要求。给定时间点的最佳设置可能会在很长一段时间内保持可行。
与共识形成相关的属性值得牢记。如 第 8 节 所示,委员会轮换率 R 随着添加辅助验证器的数量而迅速下降。从共识的角度来看,最好能够进一步描绘出 R 的更具体的要求,包括现有的链和最终性工具。在某些方面,与活动比率 a_r 相关的要求更容易理解;孤立地考虑时,更高的比率更好,因为它减少了紧张关系和收益差异。
如果范围进一步扩大,则纯 Zipfian 质押分布的假设将变得非常可疑。如果将最低质押余额从 32 ETH 降低到 1 ETH,则质押者的数量不一定会呈指数增长。原因之一是,随着质押余额的减少,运行验证器的固定成本最终会超过收益收入。例如,当仅关注固定成本时,如果运行 32-ETH 验证器需要 1% 的收益才能保持盈利,那么运行 1-ETH 验证器将需要 32% 的收益。在考虑允许 1-ETH 验证器的举措时,需要记住的另一点是它会降低活动比率 a_r。与此同时,允许资金较少的用户成为共识过程的积极参与者当然具有根本价值,并且是值得努力的方向。
附录 A:Zipf 分布
A.1 纯 Zipf 分布下的质押者数量
对于较大的 N,调和级数
1 + \frac{1}{2} + ... + \frac{1}{N}
接近 \ln(N)+\gamma,其中 \gamma 是Euler-马歇罗尼常数,约为 0.577。质押总量为
D = 32N(\ln(N)+\gamma)
现在的任务是在给定特定 D 的情况下推导出 N。令 u = \ln(N) + \gamma。那么 N = e^{u - \gamma},并且可以重新排列该等式,如下所示:
\frac{D}{32}e^\gamma = u e^{u}
使用 Lambert W 函数的定义,它给出 u = W(z),其中
z = \frac{D}{32} e^\gamma:
u = W \left( \frac{D}{32} e^\gamma \right)
回想一下 u = \log(N) + \gamma。将其代入得到
\log(N) + \gamma = W \left( \frac{D}{32} e^\gamma \right),
因此
\log(N) = W \left( \frac{D}{32} e^\gamma \right) - \gamma.
最后将两边取幂以求解 N:
N = e^{ W \left( \frac{D}{32} e^\gamma \right) - \gamma}
该等式提供了一种在给定 D 的情况下推导 N 的简单方法,以便可以根据先前的规范使用调和级数形式的基线 Zipfian 分布。以下两行 Python 代码为特定存款大小生成质押集 S,其中 eg=np.euler_gamma:
N = round(np.exp(scipy.special.lambertw(D*np.exp(eg)/(32))-eg))
S = 32*N/np.arange(1, N + 1)A.2 纯 Zipf 分布下的验证器数量
回想一下,质押者的数量如先前推导的那样
N = e^{ W \left( \frac{D}{32} e^\gamma \right) - \gamma}.
在这些 N 个质押者中,1/64 将拥有 2048 或更高的质押:
2048 = \frac{32N}{N_{h}},
N_{h} = \frac{N}{64}.
在理想情况下,该质押将被分为
V_{h} = \frac{1}{2048}\sum_{n=1}^{N_h} \frac{32N}{n} = \frac{32N}{2048} \cdot (\ln(N/64) + \gamma) = \frac{N}{64} \cdot (\ln(N/64) + \gamma)
个验证器。但是,由于将质押拆分为其最后一个验证器时的浪费(即,小数部分的累积效应),\frac{N}{64} 个质押者大约会向该数字添加预期的 \gamma 个验证器。有 63N/64 个质押者拥有的 ETH 少于 2048 个。因此,在纯 Zipfian 分布下,质押者最大程度地合并的验证器总数为
V=\frac{N}{64} \left(63+\ln(N/64) + 2\gamma \right).
该等式是一个相当精确的近似值。例如,在 30M ETH 时,概述的过程给出 88065 个验证器,并且该等式(在第一步中对 N 进行四舍五入后)给出 88065.385 个验证器。
附录 B:预测与评估
B.1 评估程序
通过一个布尔掩码来模拟一个块的累积最终性,该掩码迭代委员会,进入每个在特定插槽/委员会之前和包括该插槽/委员会在内的所有看到的验证器。因此,起点是第一个已处理插槽的委员会中所有验证器的二进制掩码。然后,该操作通过 epoch 的插槽进行,将先前未见过的验证器从委员会输入到适用于特定插槽的二进制掩码。然后在每个插槽中对最终确定的验证器进行求和,从中计算出 D_f,从而计算出 \widetilde{F}_ {\! g}。为了获得最佳精度,评估以循环方式执行,如先前所述。如果 S_{\text{ep}} 很高,则可以限制要评估的起始点的数量上限,例如,从每隔一个或每隔三个插槽开始。用于第 6 节的评估使用了十个不同起始点的限制。
一种潜在的优化方法是还计算一个单独的掩码(或索引列表),该掩码仅指定每个插槽新出现的验证器。该掩码/列表指定验证器是否存在于当前委员会中ANDNOT存在于计算到先前委员会的累积最终性掩码中。好处是只能对新添加的验证器进行求和,随后加上在先前插槽/委员会导出的累积和。
B.2 加权聚合最终性差距
聚合最终性差距 \widetilde{F}_ {\! g} 通常看起来像一个均衡的优化标准。但是,在某些情况下,可能需要优先考虑初始插槽中的高最终性(从而也减慢轮换速度),而在其他情况下,可能更喜欢整体上较短的达到完全最终性所需的时间(从而也增加第 8.3 节中讨论的活动比率)。因此,加权聚合最终性差距可能很有用。本文使用了一种加权,该加权提供了平均而言稍微较短的达到完全最终性的时间。这有助于解决对数正态集合(附录 B.4)中的边缘情况,在这些情况下,该机制非常接近完全最终性,但最终确定的最后一部分花费了几个插槽。但是,也可以朝着相反的方向进行探索,例如,考虑与轮换速度相关的要求。
定义一种可以在 2 个常规插槽中实现完全最终性的场景,但添加了两个辅助验证器,如 {2|4} 所示。加权旨在同等地影响以下结果:{2|4}、{4|7}、{10|15} 和 {21|28}。{a|b} 的加权为:
w = \frac{b\sqrt[3]{b-a}}{ka}.
常数 k 设置为 2^6,并且该权重应用于每个评估的辅助插槽数。这可以通过两种方式完成:\widetilde{F}_ {\! gw} = \widetilde{F}_ {\! g}(1+w) 或 \widetilde{F}_ {\! gw} = \widetilde{F}_ {\! g} \ +w,本文中使用了第一种方式。
B.3 插值后的实际值
用于建模的实际值不是辅助委员会 C_{\text{aux}},而是要添加的辅助验证器的数量 V_{\text{aux}}。C_{\text{aux}} 通常不适合作为实际值的主要原因是与图 11-12 中类似鳍状的模式有关。最佳 C_{\text{aux}} 将在常规委员会需要一个以上常规插槽的边界处移动,导致实际值随着 D 的增加而振荡。以辅助验证器为目标可以避免此问题。图 14 中显示的总委员会数 C 也可以使用,但这排除了将带有 \widetilde{F}_ {\! gw} 的抛物线插值用于常规委员会作为插值点之一。
剩余的问题是,最小化 \widetilde{F}_ {\! gw} 的 V_{\text{aux}} 被离散为步长为 \hat{V}_ {\!a} 的步长,因为最小值只能在 C_ {\text{aux}} 的整数处定义。将最小化 \widetilde{F}_ {\! gw} 的辅助委员会数定义为 C^*_{\text{aux}}。跨越三个相邻点执行抛物线插值,\widetilde{F}_ {\! gw}(C^*_{\text{aux}}-1), \widetilde{F}_ {\! gw}(C^*_{\text{aux}}) 和 \widetilde{F}_ {\! gw}(C^*_{\text{aux}}+1) 以得出相对位置:
w_{V} = \frac{\widetilde{F}_ {\! gw}(C^*_{\text{aux}}+1)-\widetilde{F}_ {\! gw}(C^*_{\text{aux}}-1)}{2(2\widetilde{F}_ {\! gw}(C^*_{\text{aux}}) - \widetilde{F}_ {\! gw}(C^*_{\text{aux}}-1) - \widetilde{F}_ {\! gw}(C^*_{\text{aux}}+1))}.
将 V_{\text{aux}}(C^*_{\text{aux}}) 定义为在最佳辅助委员会数下的辅助验证器数。实际值 V^{y}_{\text{aux}} 由相邻值的 w_{V} 加权平均值给出。因此,如果 w_{V}<0,则变为
V^{y}_{\text{aux}}=V_{\text{aux}}(C^*_{\text{aux}}-1)(1-w_{V}) + V_{\text{aux}}(C^*_{\text{aux}})w_{V},
如果 w_{V}>0,则应用相应的加权。第 7 节中辅助验证器数量的预测相应地定义为 V^{x}_{\text{aux}}。
B.4 生成对数正态分布的验证器集
为了提供更多种类的验证器集示例,生成了一个具有对数正态分布的附加集。首先从以 400 ETH 为中心且标准差为 128 ETH 的正态分布中抽取平均值 \mu_{\mathcal{V}},并将其限制在 s_{\text{min}} = 32 ETH to s_{\text{max}} = 2048 ETH 的范围内。接下来,对数正态分布的标准差 \sigma 从区间 [0, 3] 中均匀抽取。为了提供根本没有可变性的验证器集的边缘情况,任何低于 0.2 的 \sigma 都设置为 0。
给定选定的平均值 \mu_{\mathcal{V}} 和标准差 \sigma,对数空间 \mu 中对数正态分布的平均值计算为
\mu = \ln(\mu_{\mathcal{V}}) - \frac{\sigma^2}{2},
目的是使原始空间中的平均值接近 \mu_{\mathcal{V}}。然后,通过从由参数 \mu 和 \sigma 定义的对数正态分布中采样来生成最多所需质押量 D 的验证器,从而确保每个生成的验证器都保持在 s_{\text{min}} 到 s_{\text{max}} 的范围内。
- 原文链接: ethresear.ch/t/vorbit-ss...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 影响市场:解决预测市场衍产品的“如何”和“为什么” 371 浏览
- 证明者网络格局:Succinct和Boundless网络对比分析 2048 浏览
- 以太坊 - | ACP | 77提案 | 1719 浏览
- SIMD-228:一项关键分析 2742 浏览
- 释放SAS的下一个阶段:介绍svmBNB链 1839 浏览
- EigenLayer如何防止以太坊Electra升级中的关键验证者风险 1426 浏览
- DoubleZero :更快的互联网 2560 浏览
- 以太坊协议可能的未来 #1:The Merge 2574 浏览
- 探索Liquity V2:去中心化借贷 1910 浏览
- 应用代币的现金流:一种新模型 1895 浏览
- 单Slot最终性研究 1197 浏览
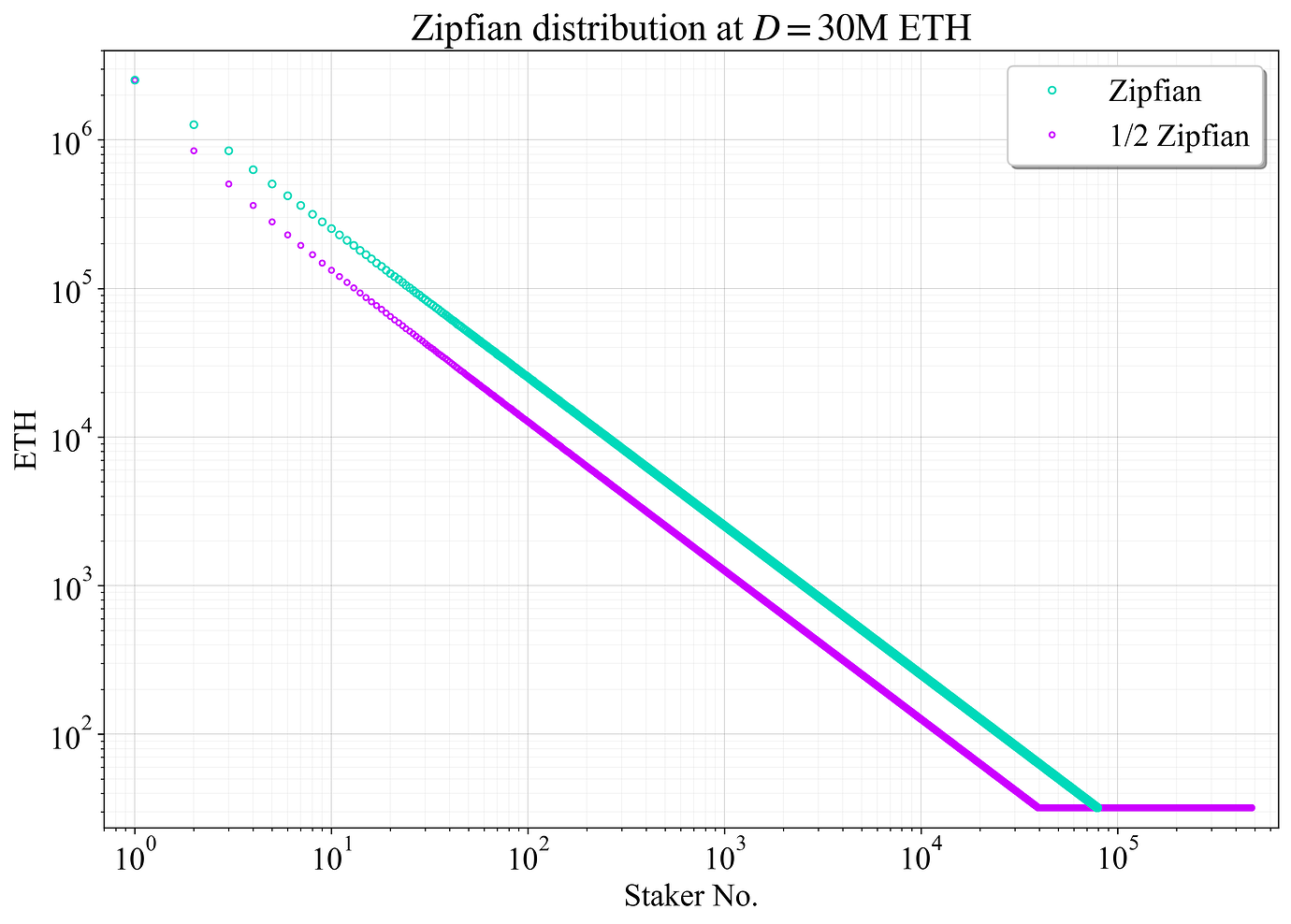 \
Figure 13067×2199 229 KB
\
Figure 13067×2199 229 KB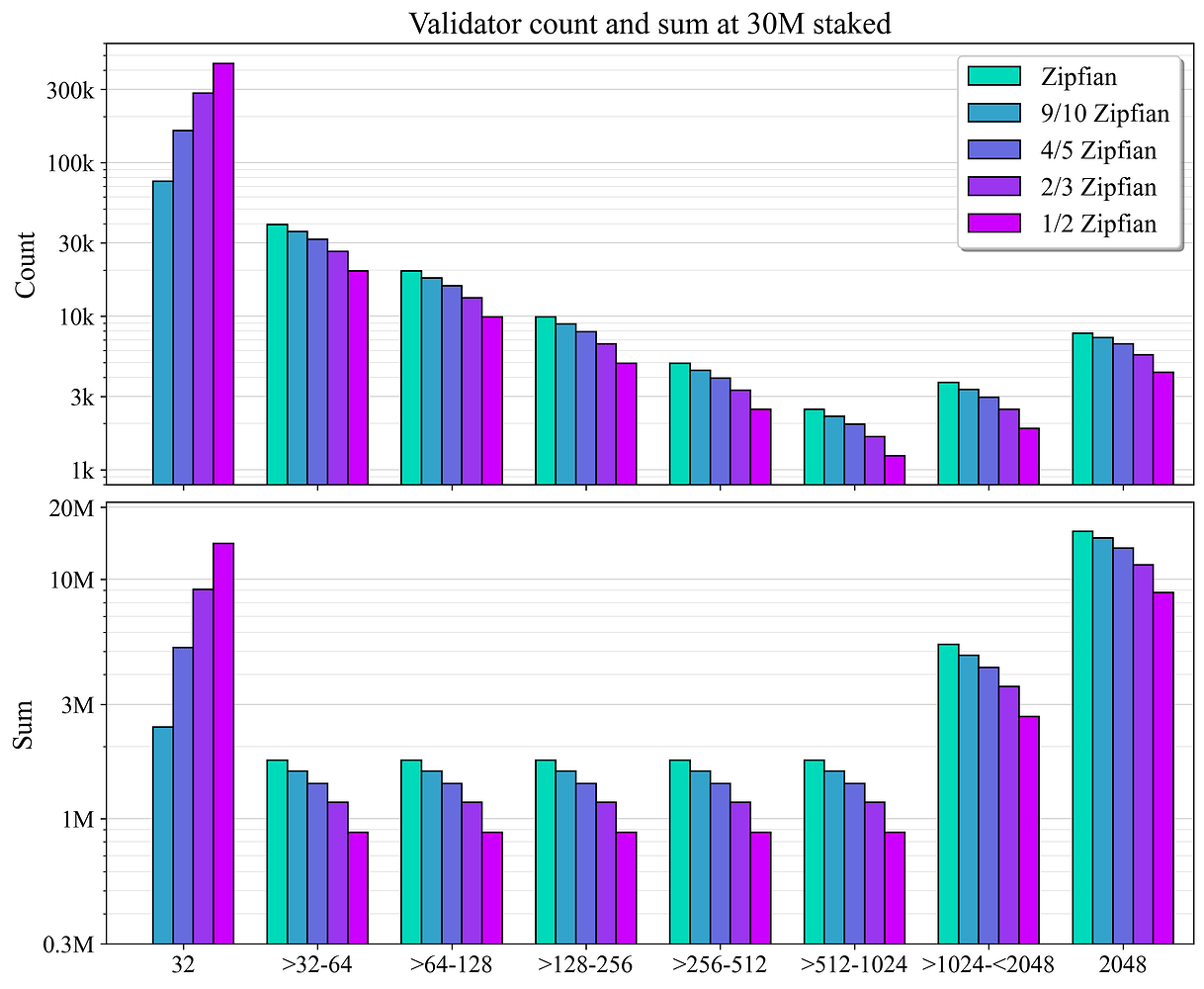 \
Figure 23094×2537 202 KB
\
Figure 23094×2537 202 KB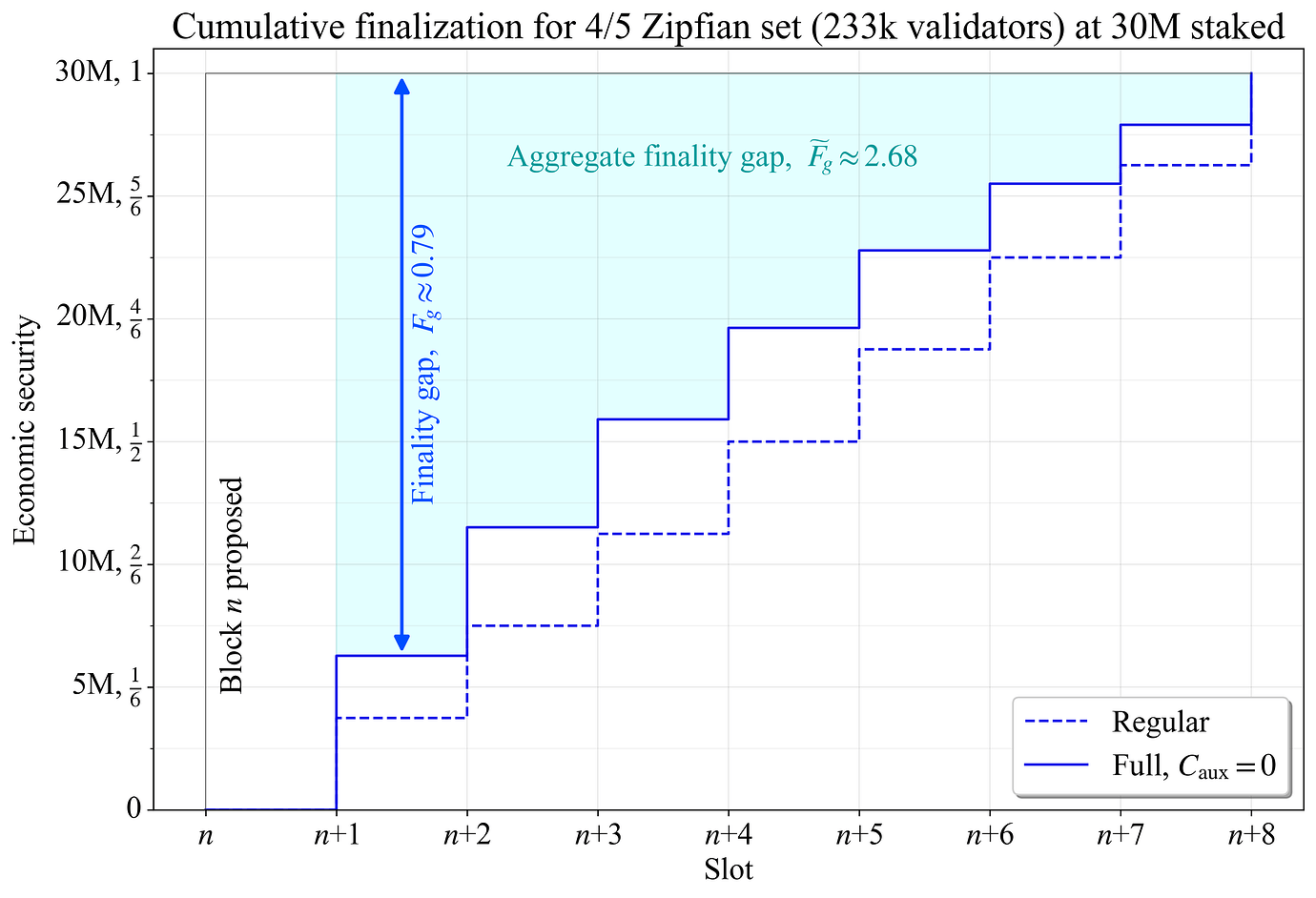 \
Figure 33192×2180 272 KB
\
Figure 33192×2180 272 KB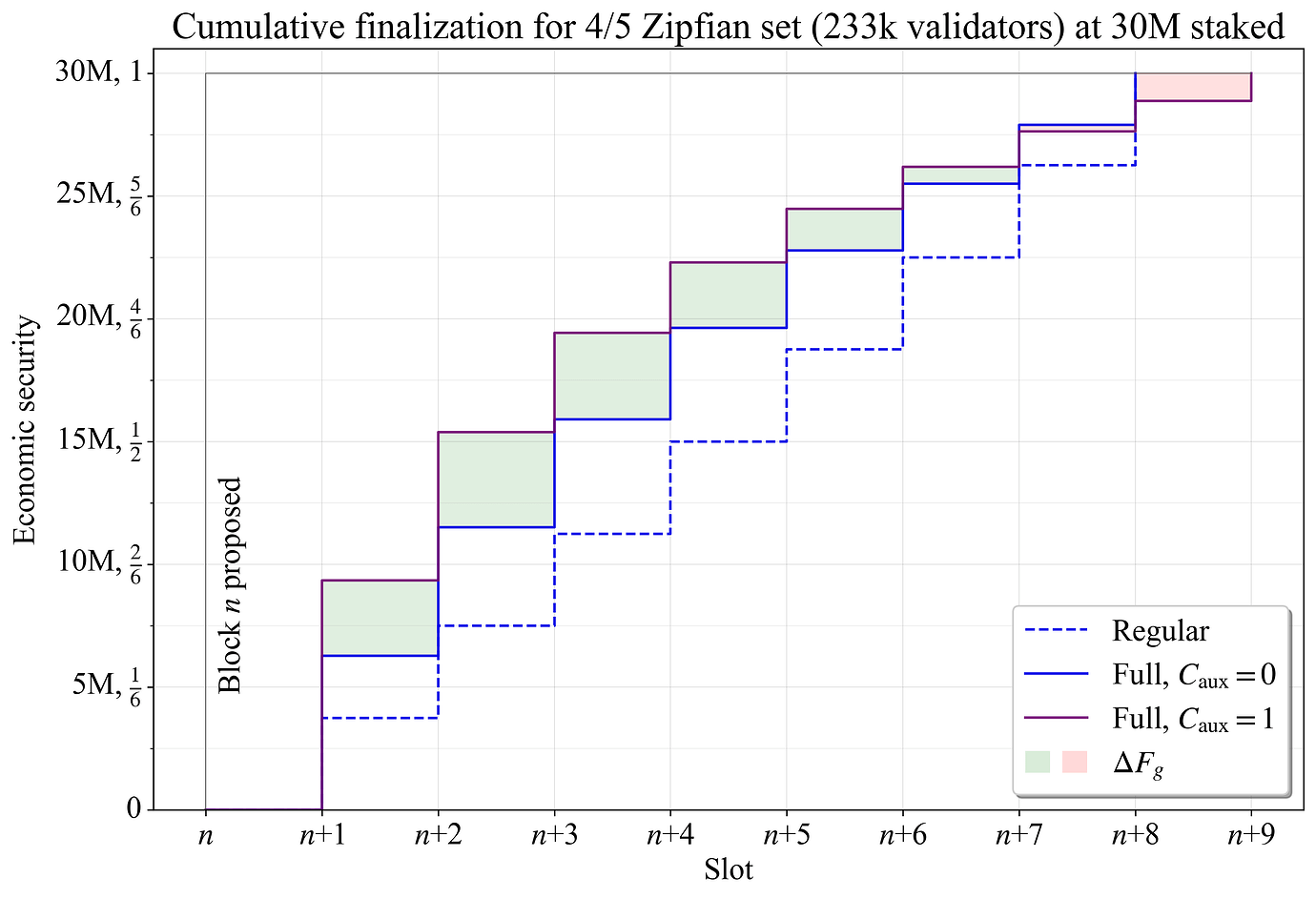 \
Figure 43192×2180 240 KB
\
Figure 43192×2180 240 KB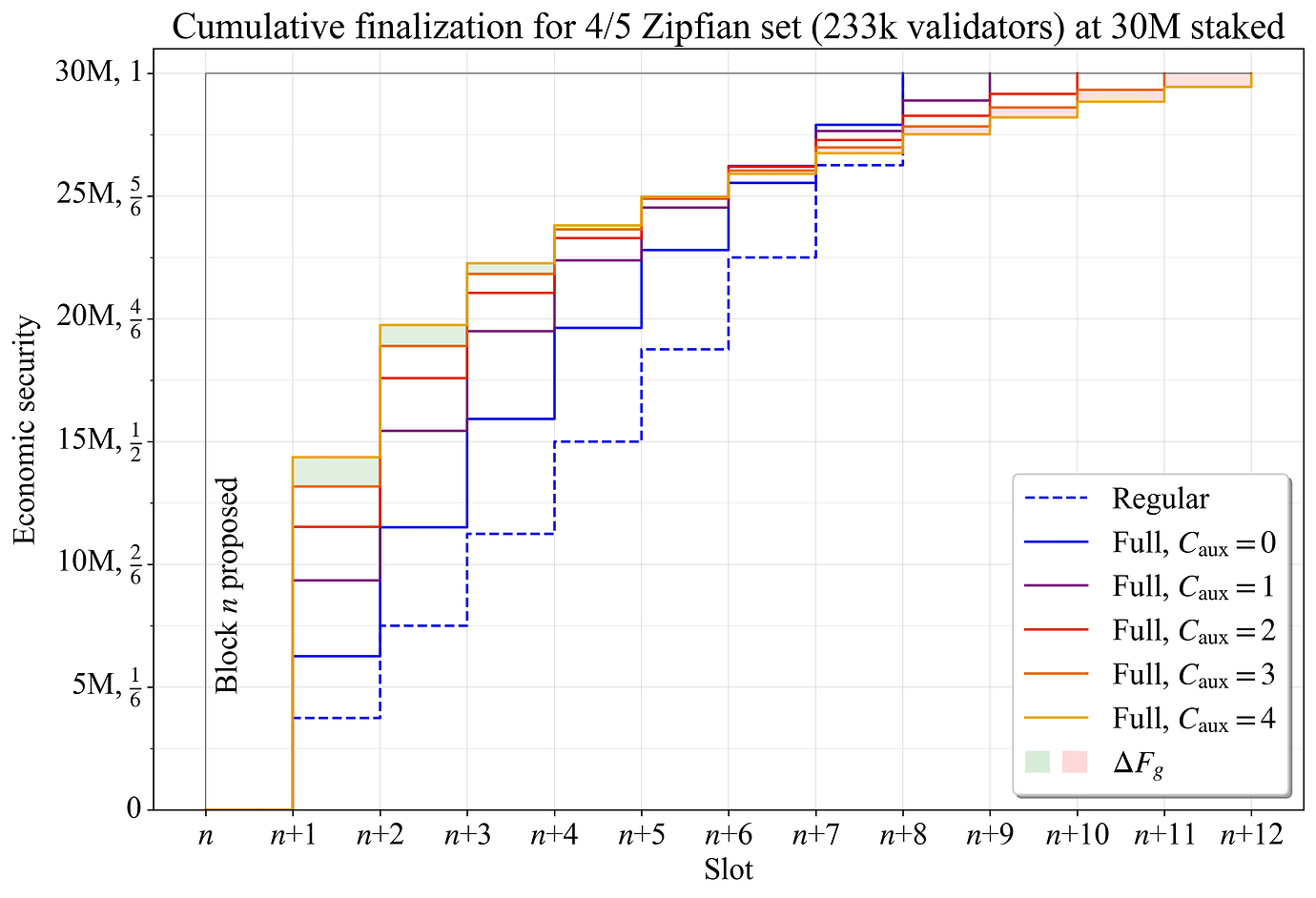 \
Figure 53192×2180 269 KB
\
Figure 53192×2180 269 KB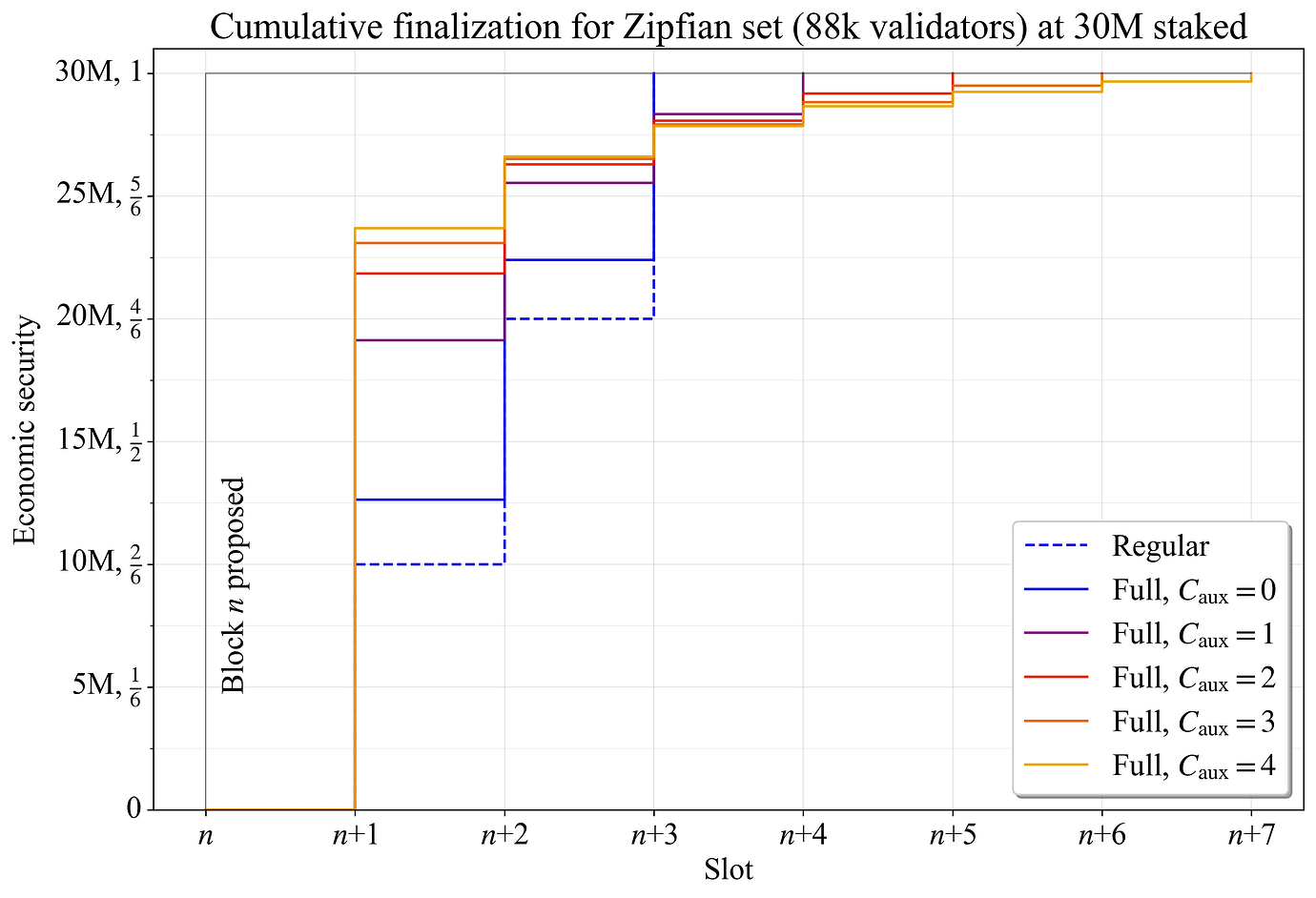 \
Figure 63192×2180 243 KB
\
Figure 63192×2180 243 KB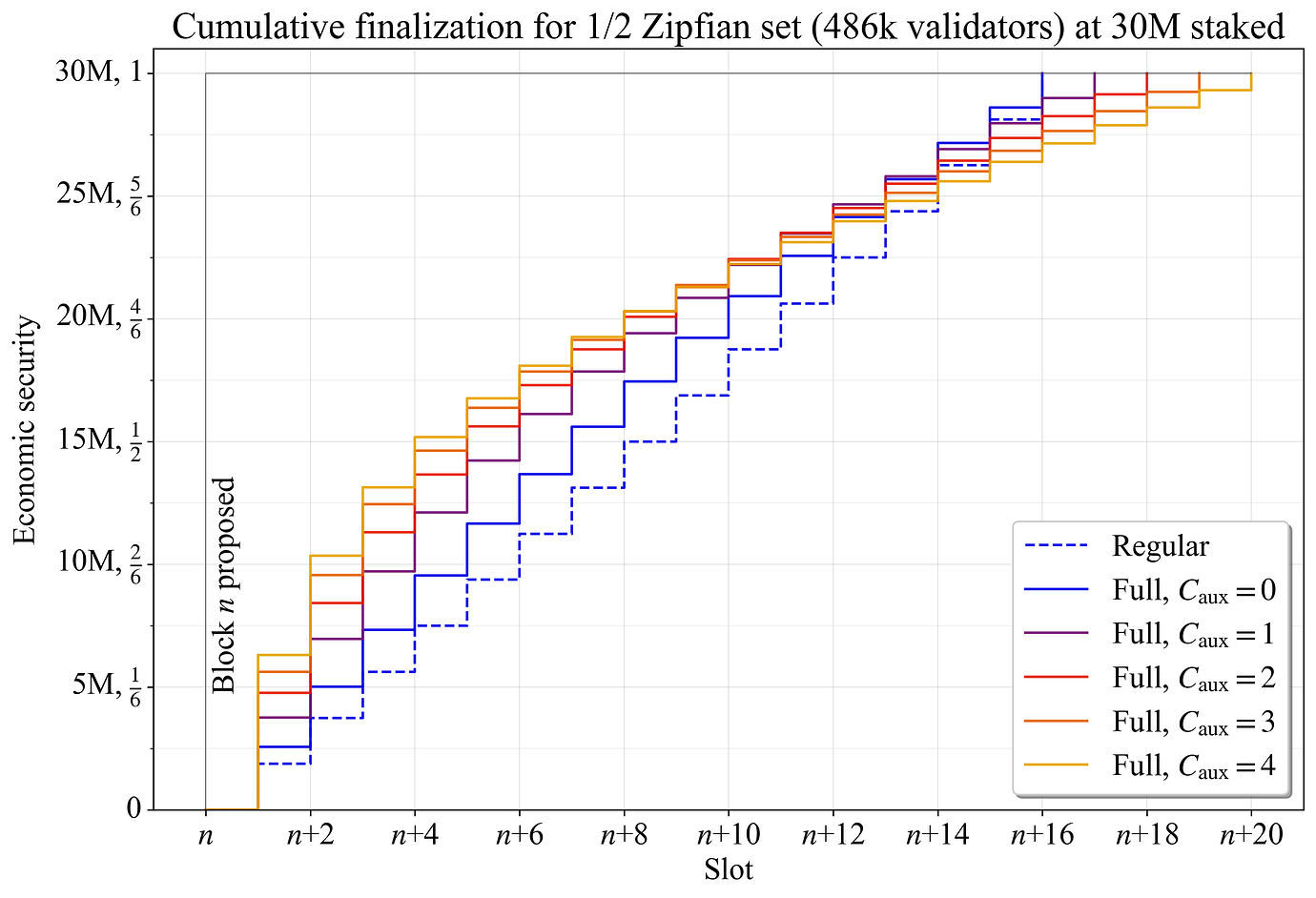 \
Figure 73192×2180 267 KB
\
Figure 73192×2180 267 KB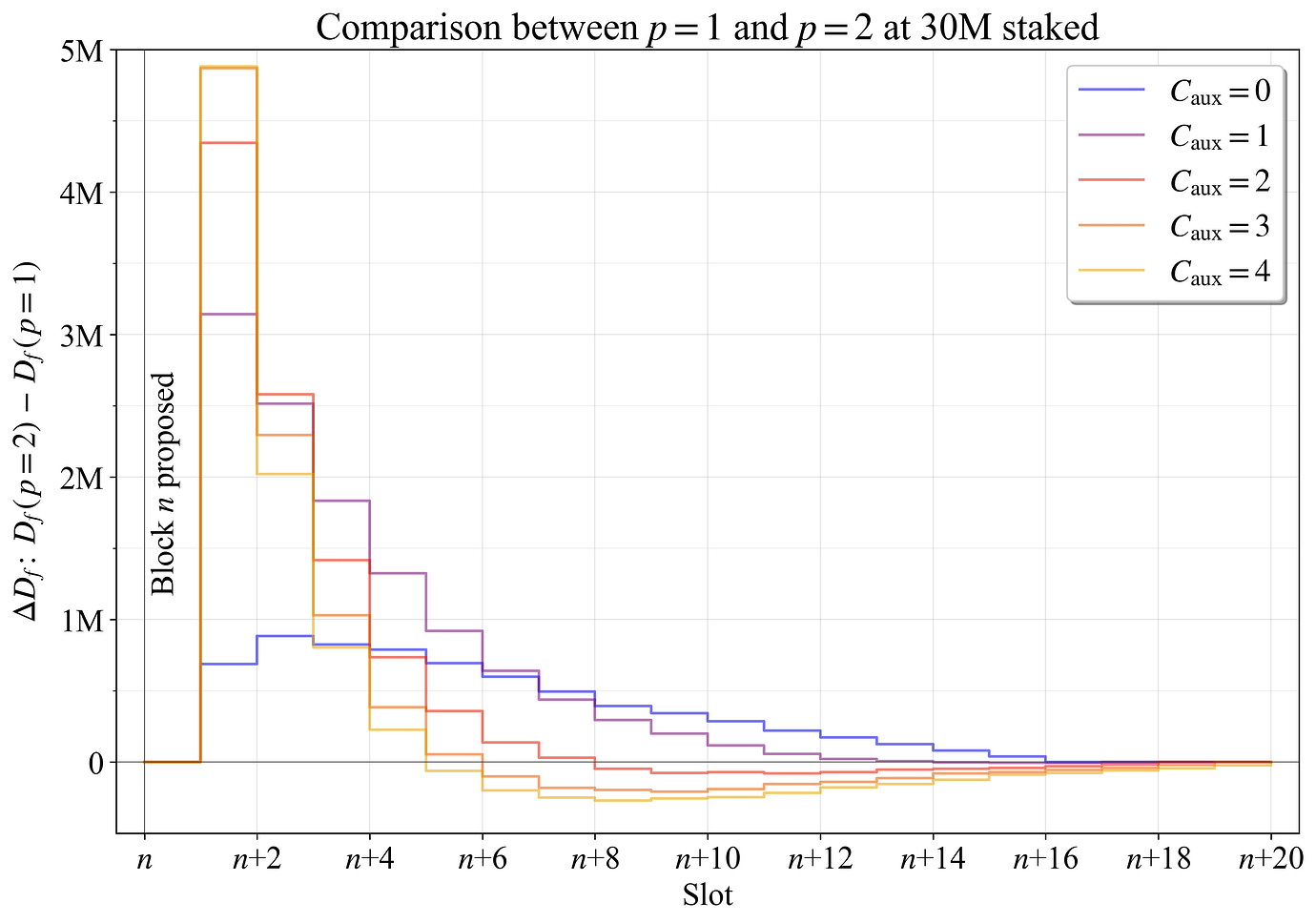 \
图 83104×2181 193 KB
\
图 83104×2181 193 KB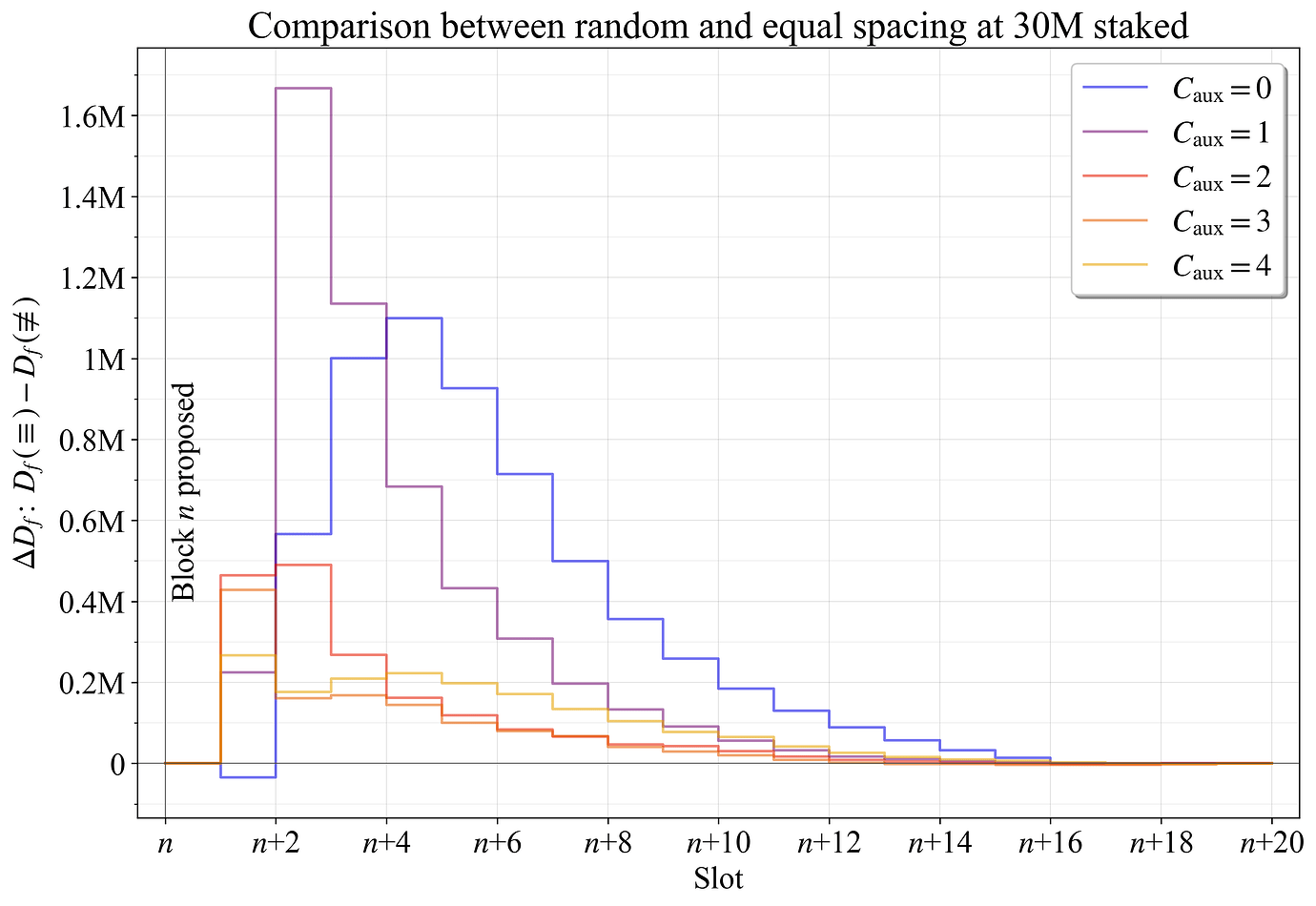 \
图 93160×2179 230 KB
\
图 93160×2179 230 KB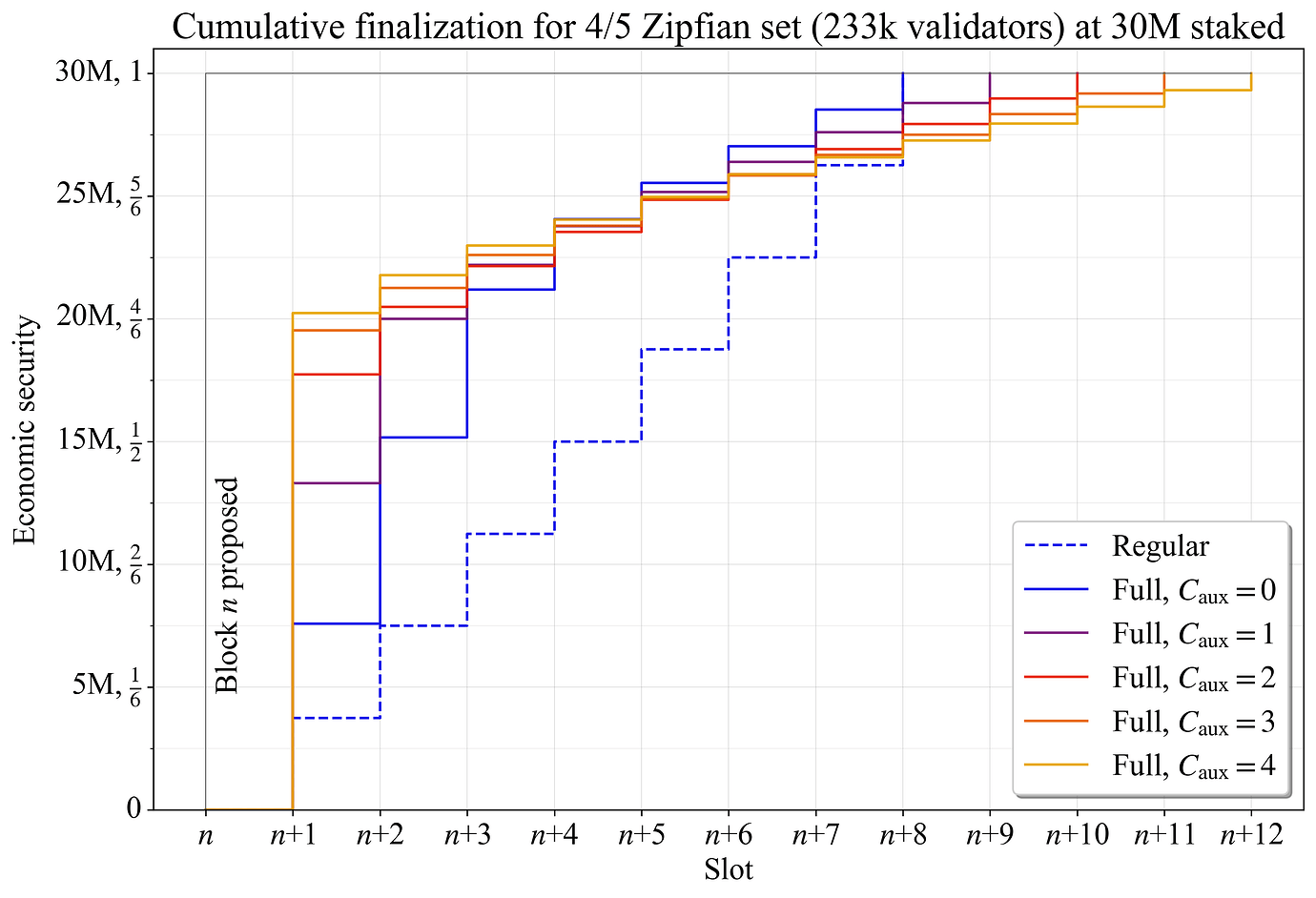 \
图 103192×2180 264 KB
\
图 103192×2180 264 KB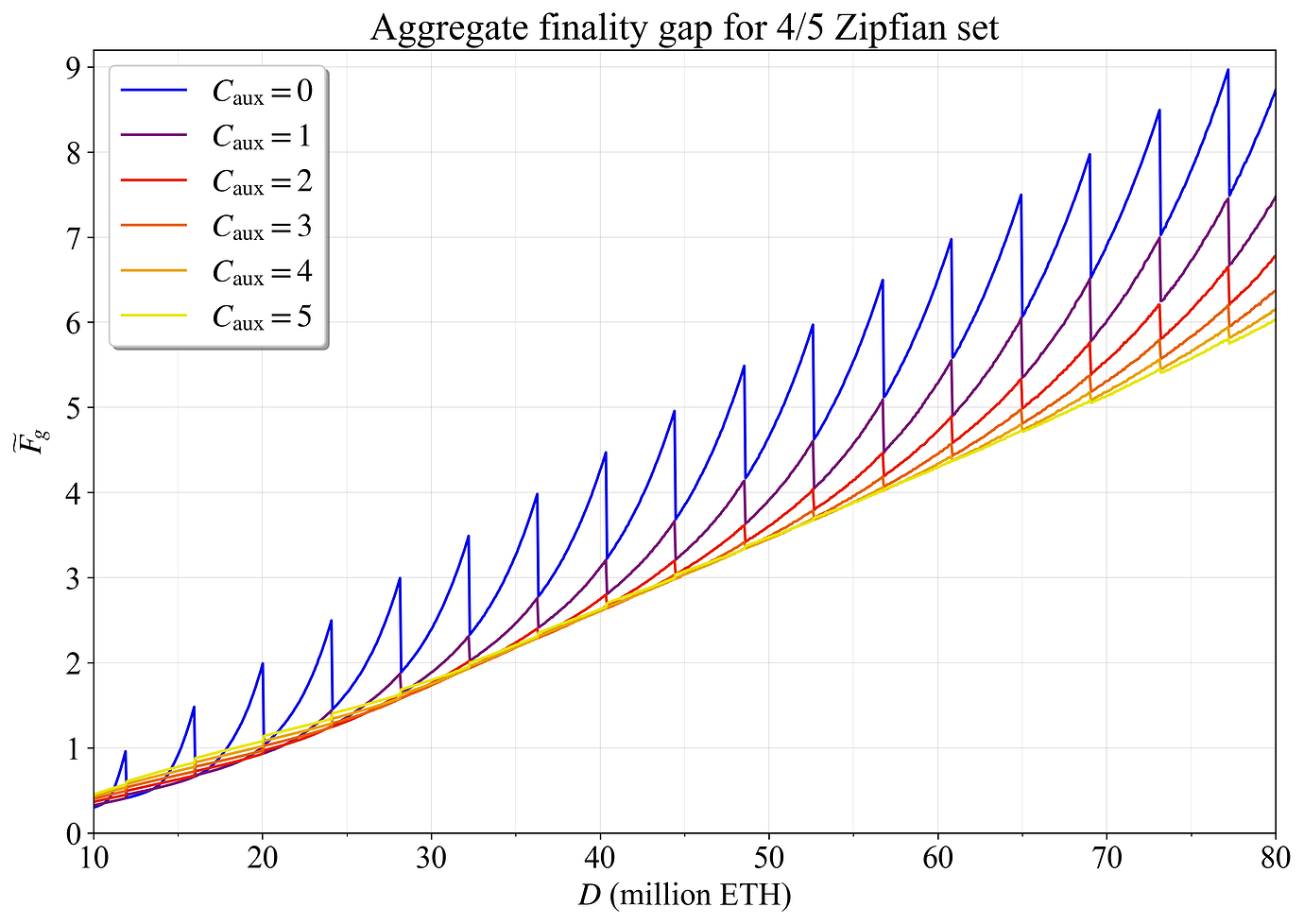 \
图 113078×2183 476 KB
\
图 113078×2183 476 KB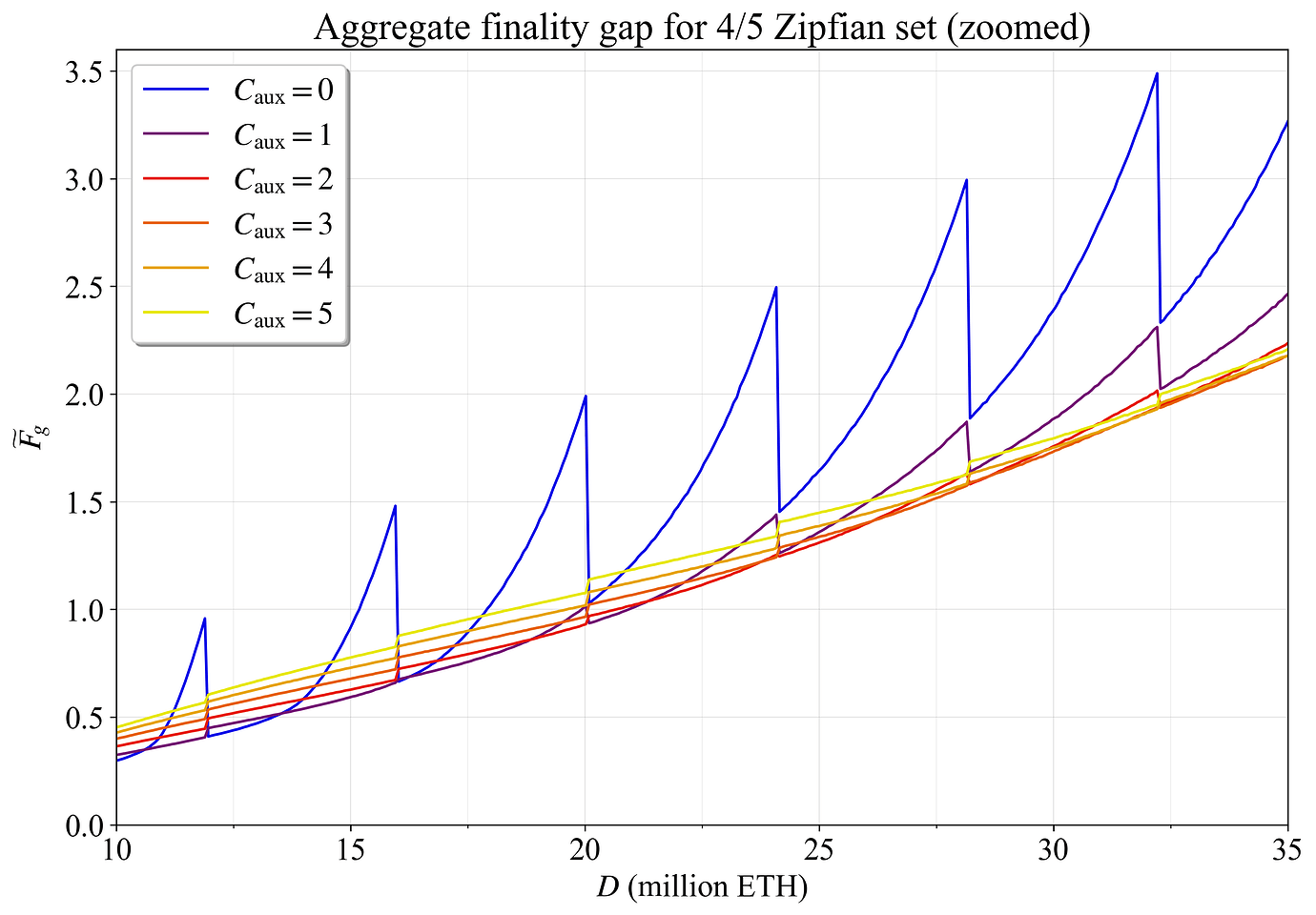 \
图 123134×2183 418 KB
\
图 123134×2183 418 KB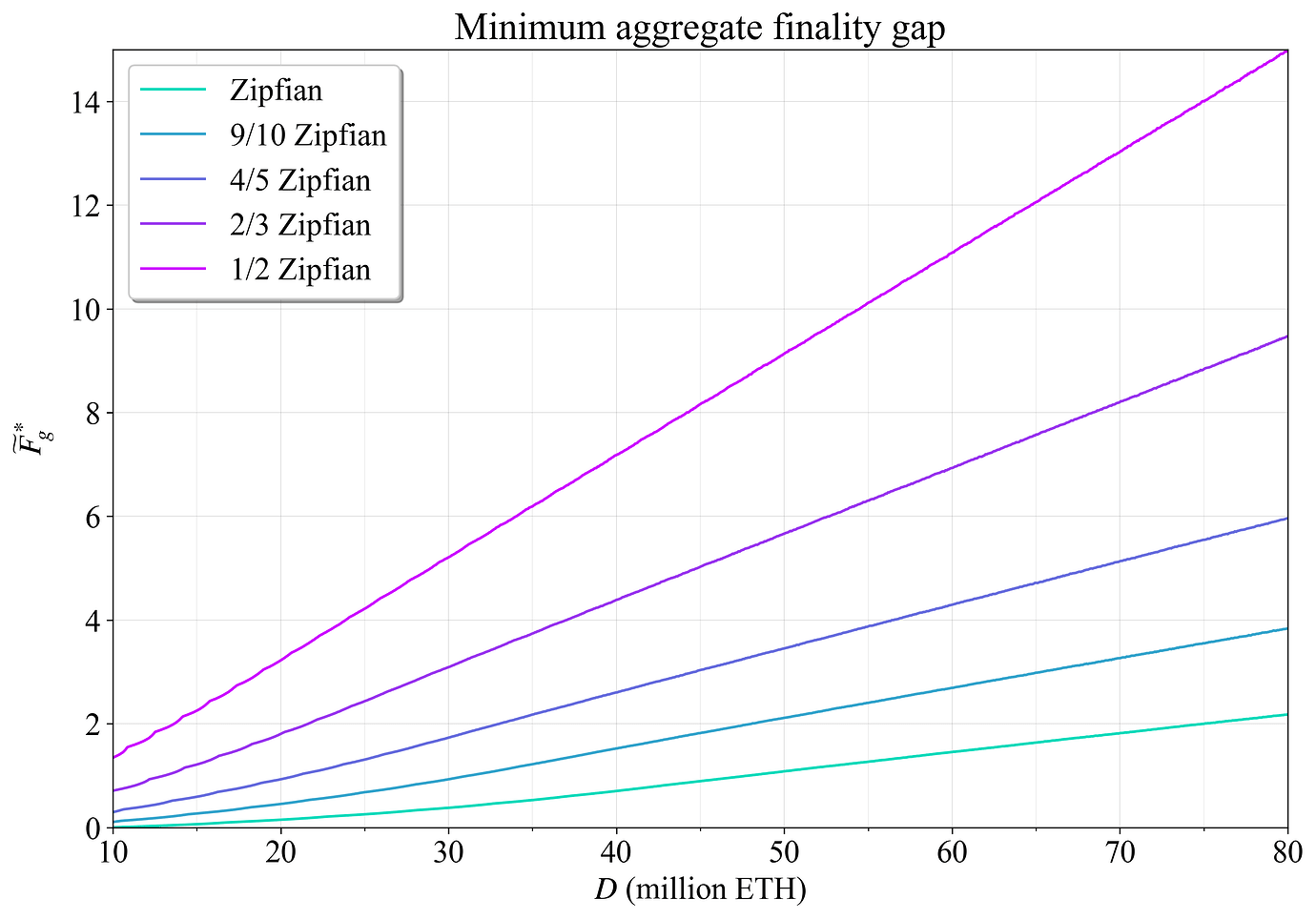 \
图 133125×2183 305 KB
\
图 133125×2183 305 KB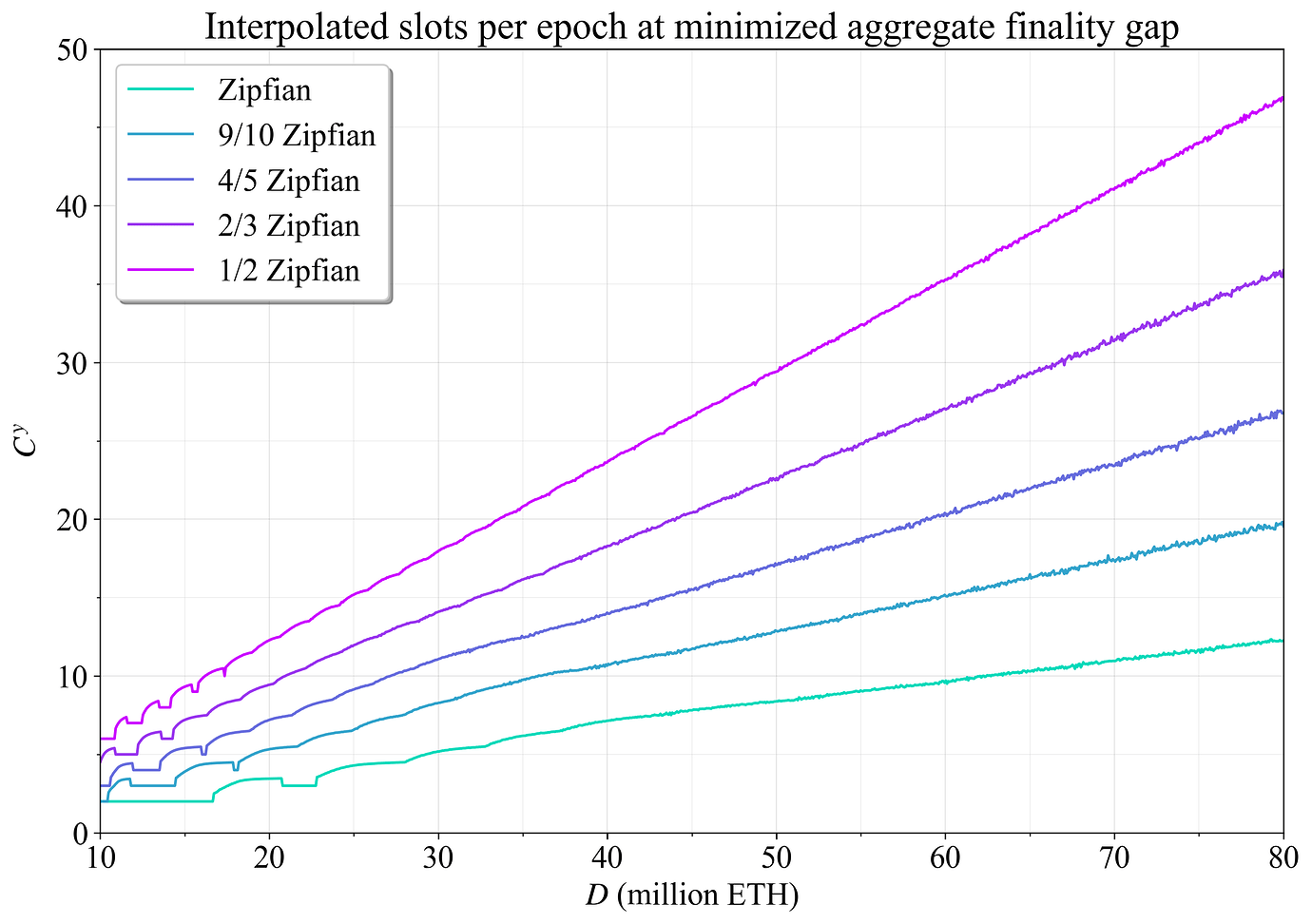 \
图 143094×2183 384 KB
\
图 143094×2183 384 KB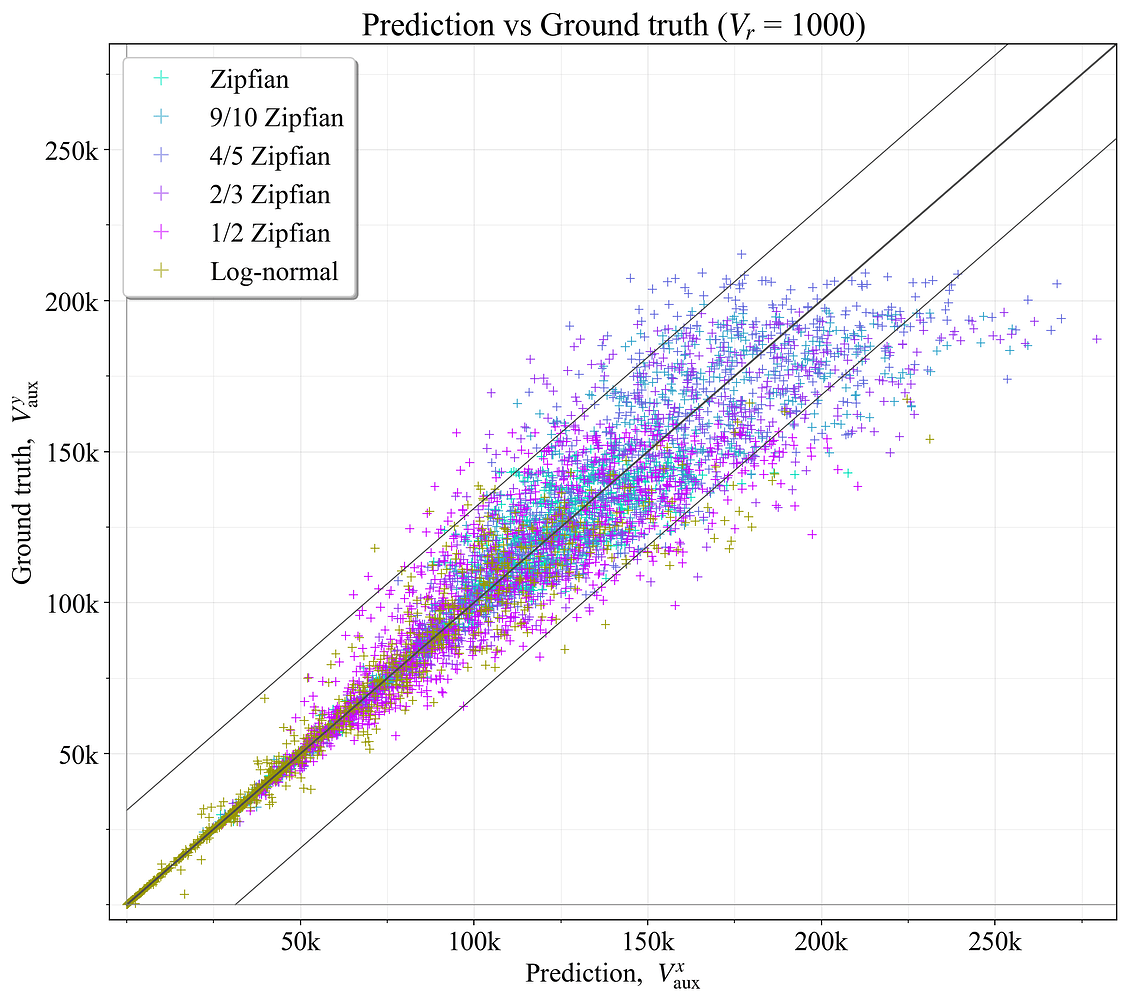 \
图 152081×1846 441 KB
\
图 152081×1846 441 KB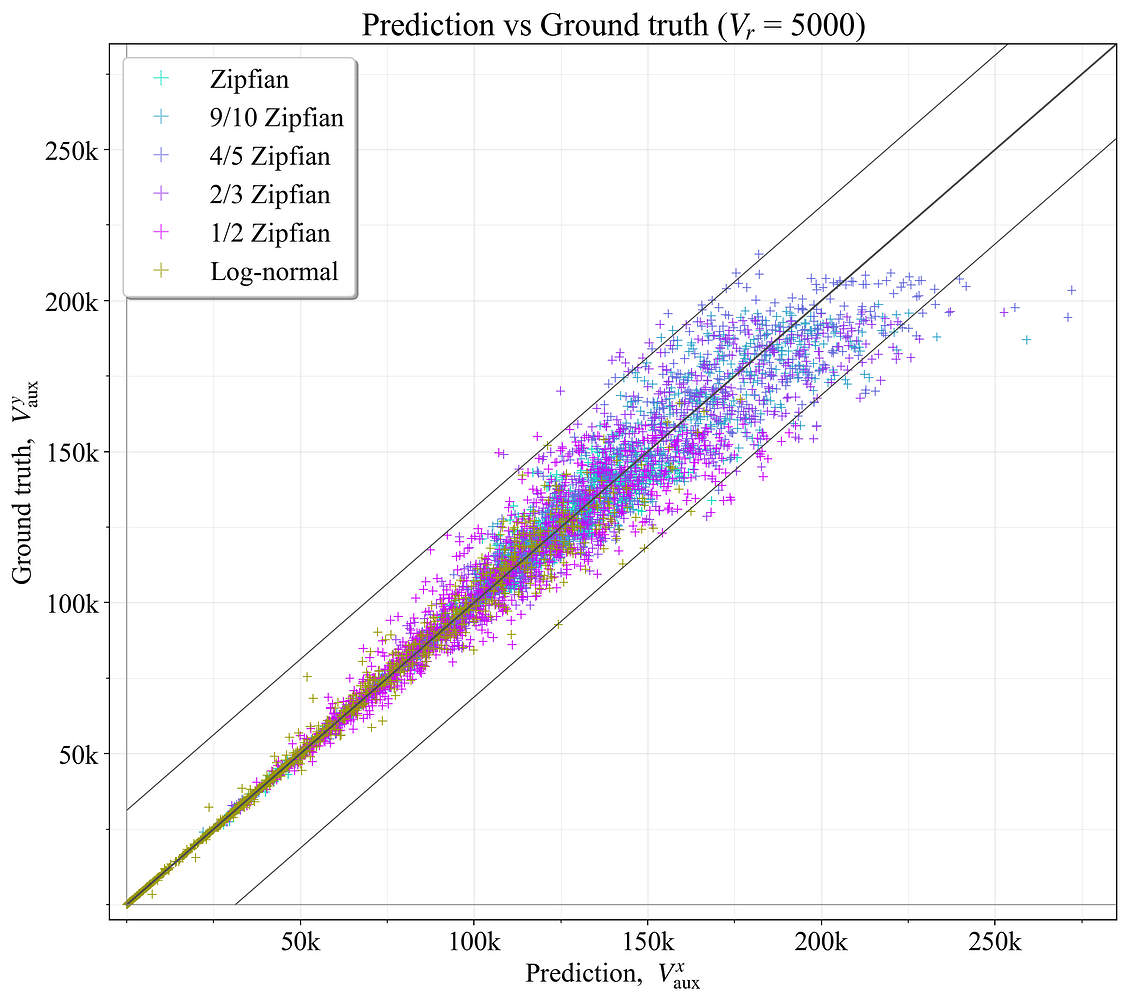 \
图 162081×1846 408 KB
\
图 162081×1846 408 KB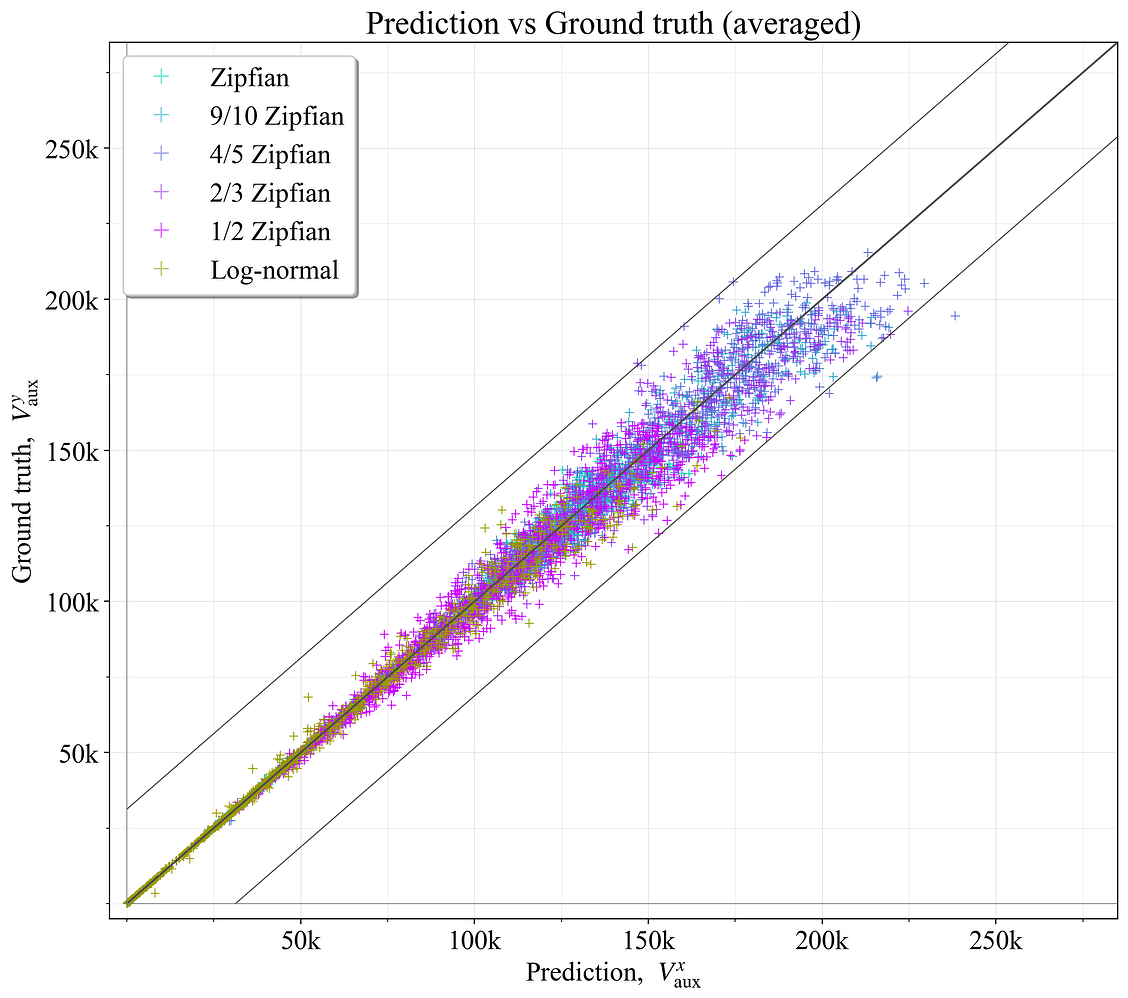 \
图 172081×1843 400 KB
\
图 172081×1843 400 KB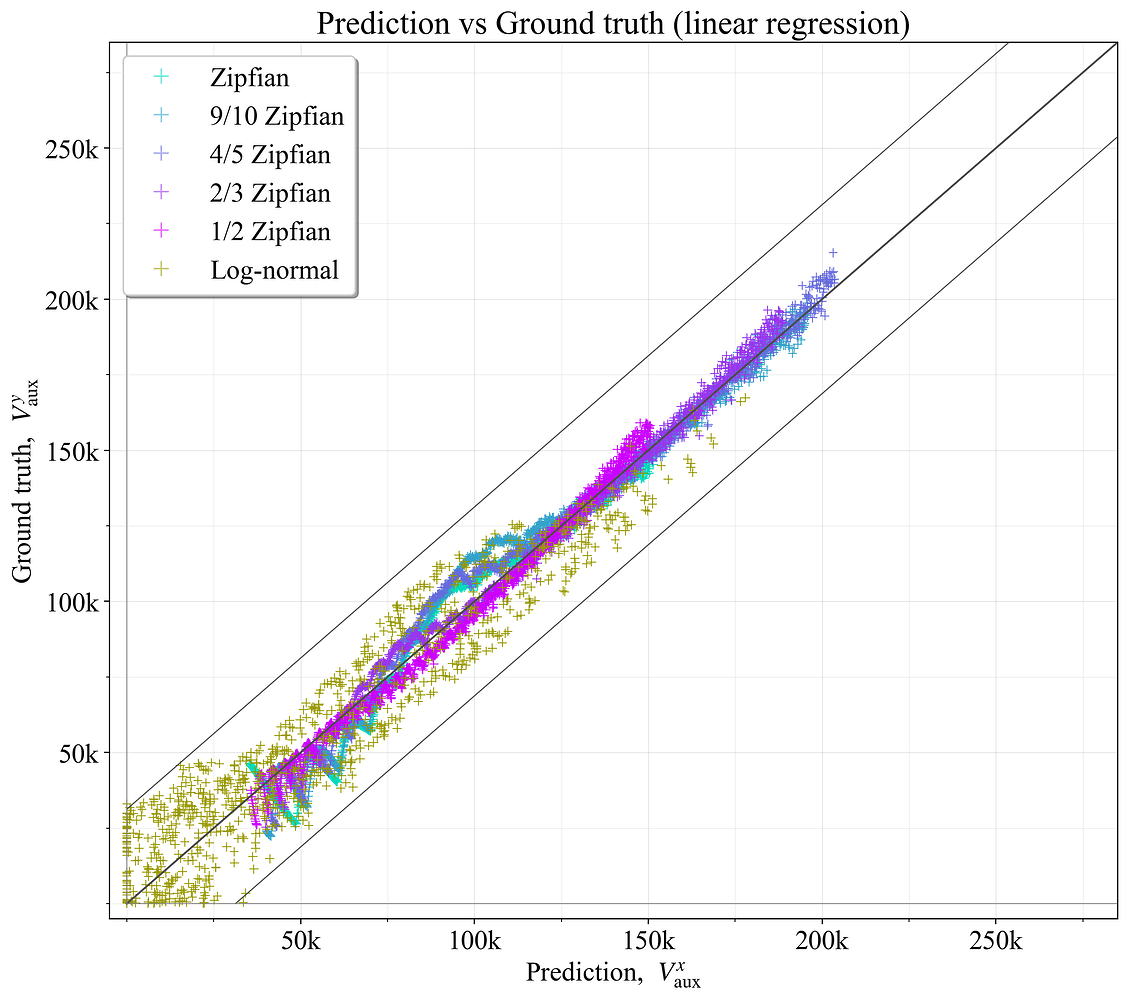 \
图 182081×1843 376 KB
\
图 182081×1843 376 KB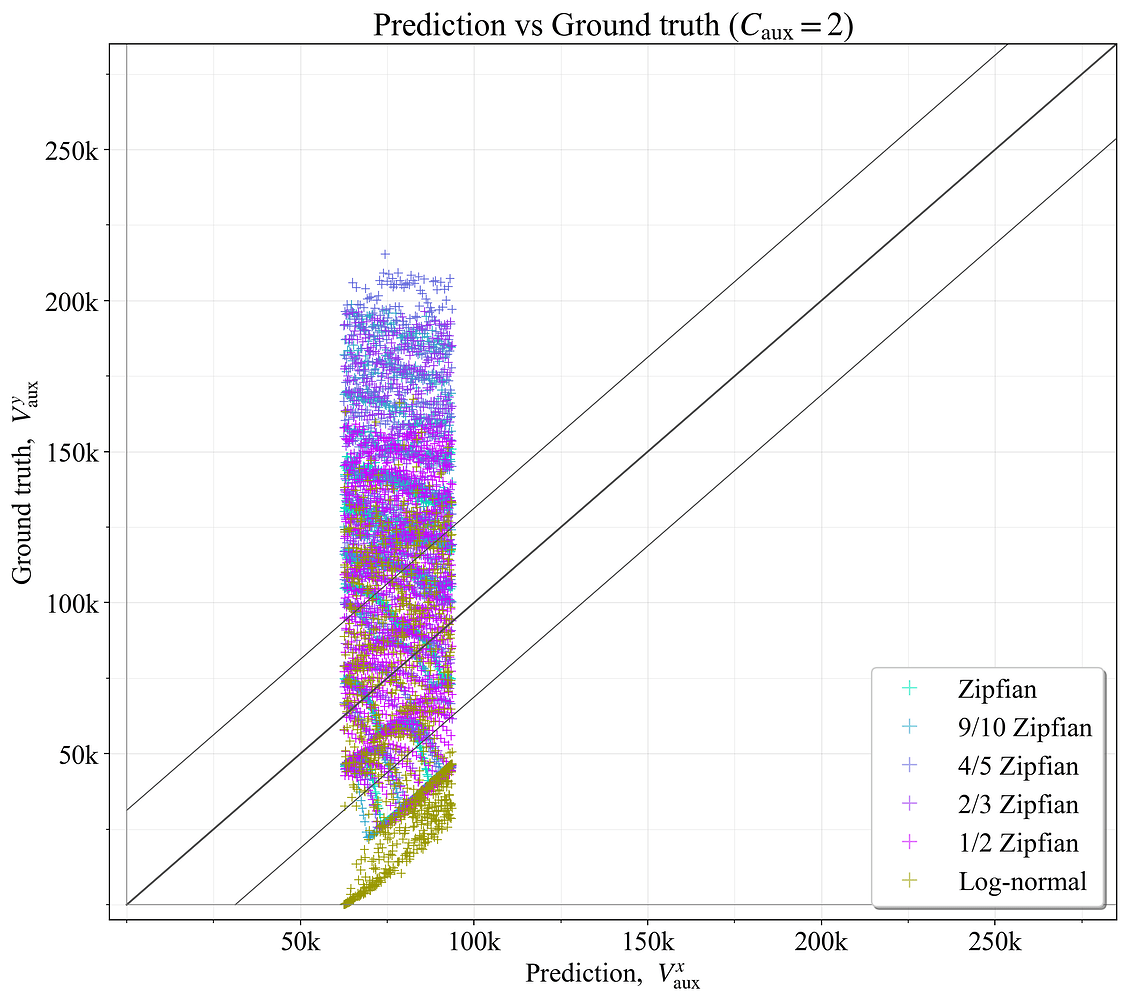 \
图 192081×1846 470 KB
\
图 192081×1846 470 KB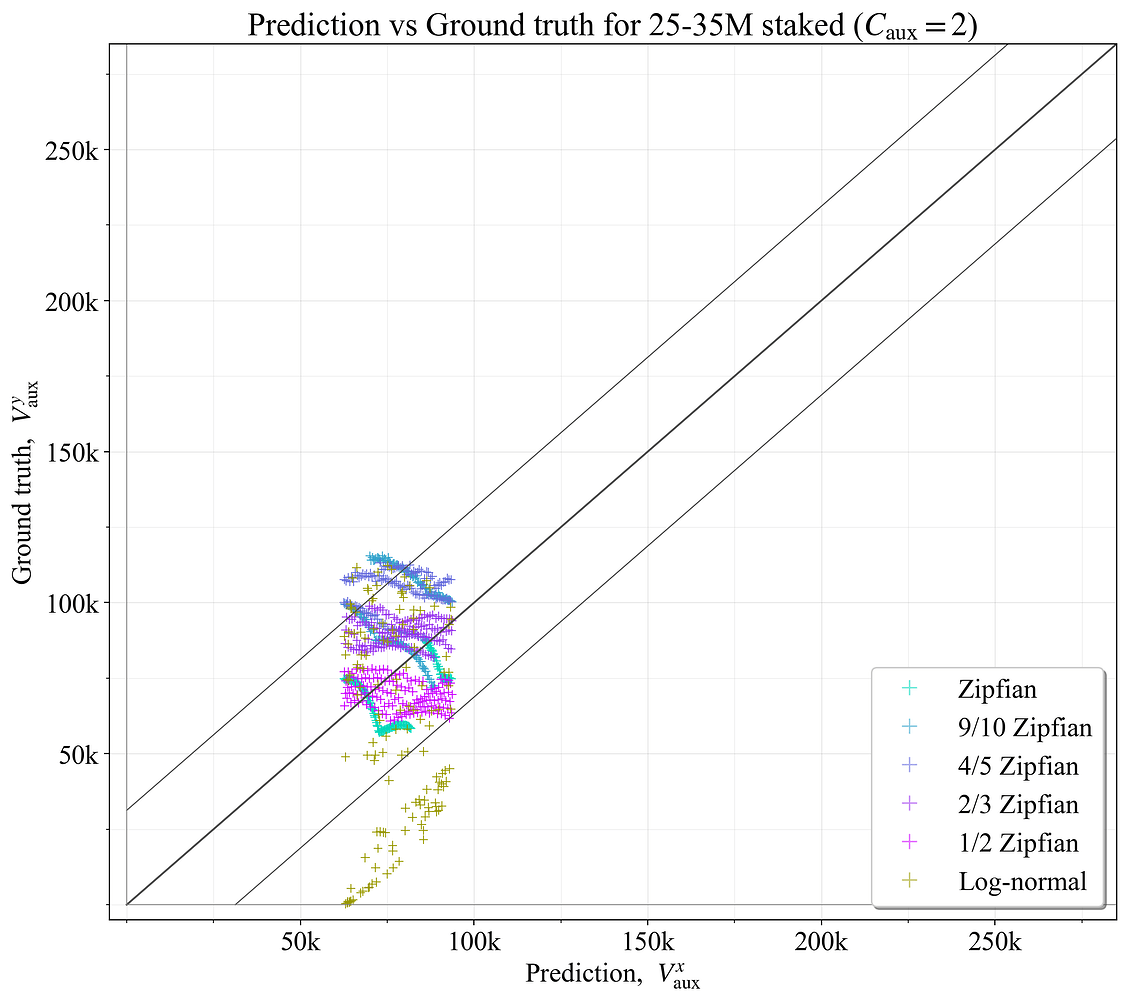 \
图 202081×1846 272 KB
\
图 202081×1846 272 KB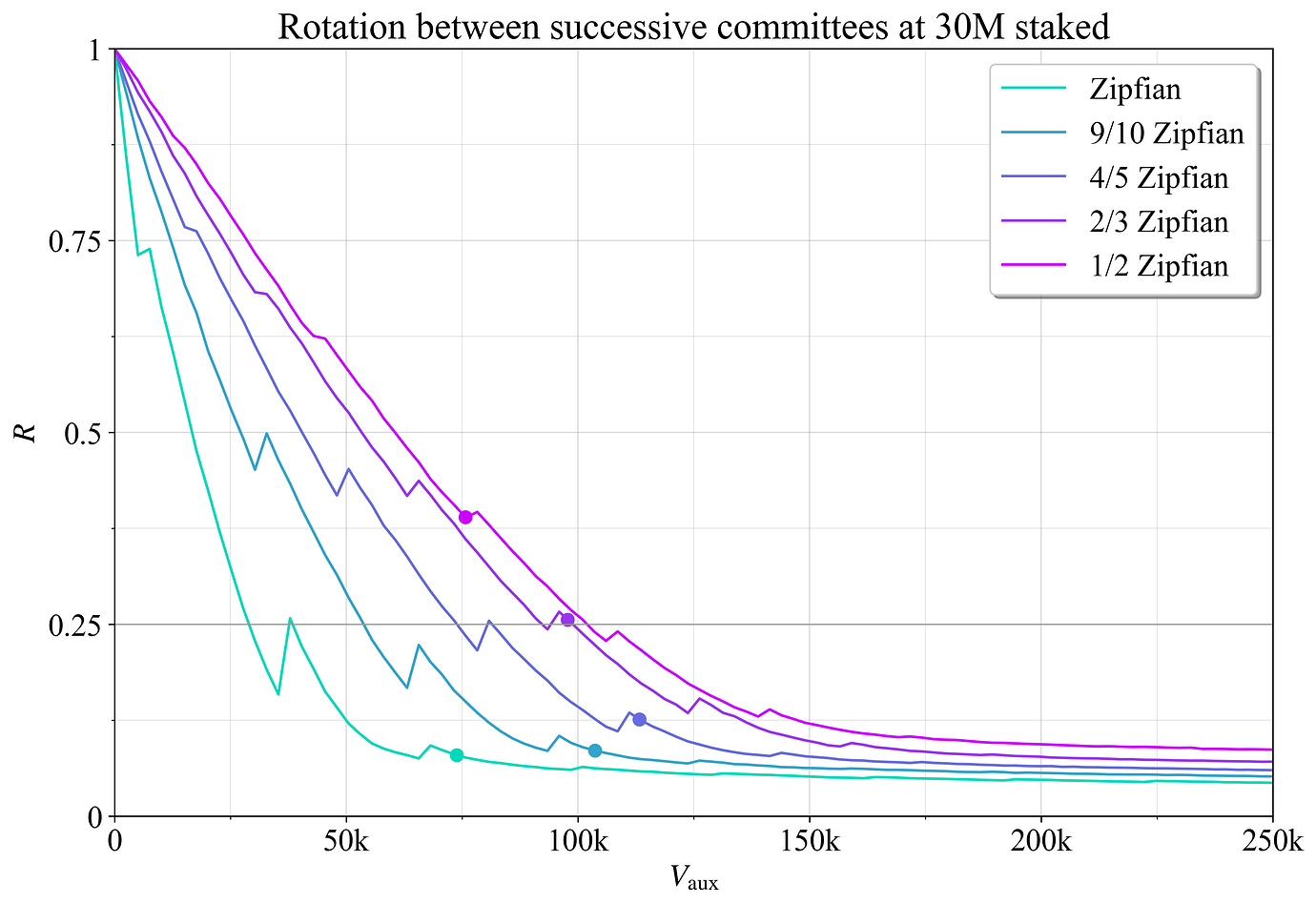 \
图 213170×2179 384 KB
\
图 213170×2179 384 KB
