常见问题解答:以太坊发行量减少 - 权益证明/经济学
- 以太坊中文
- 发布于 2024-05-30 22:45
- 阅读 951
本文是关于以太坊发行量减少的常见问题解答,讨论了减少发行量的原因、经济安全性、未来发行政策以及对staking生态的影响。文章深入探讨了不同发行策略对用户福利、网络安全和staking参与者组成的影响,并提出了若干可行的方案,包括调整奖励曲线、MEV燃烧和经济上限等。强调了在设计发行政策时,需要综合考虑各种因素,以实现以太坊的可持续发展。
常见问题解答:以太坊发行量减少
概述
当涉及到减少发行量的前提时,有许多重要的问题需要考虑。在广泛研究了这些问题之后,我认为逐一解决这些问题,并在需要时提供详细的答案,将是有益的。我在 Ethresearch 上发布是为了促进辩论,并将尝试回答你可能有的任何问题(包括适合扩展常见问题解答的新问题)。
一些之前只是顺带讨论的 staking 经济学概念,在这里会进行更广泛的探讨。这些概念包括:时间-数量策略,其中奖励曲线缓慢漂移(以及其他潜在的 endgame 策略),solo staker 和委托 staker 之间的预留收益分配,以及使用 vanilla EIP-1559 机制来针对特定 stake 参与度的缺点。所有问题的快速链接:
- 以太坊为什么要减少发行量?
- 经济安全呢?更多的 stake 会使以太坊更安全,对吗?
- 近期内理想的发行量减少是多少?
- 为什么不使用像 EIP-1559 这样的机制动态调整收益,以保证某个固定的目标参与度水平?
- 减少发行量将如何影响 staking 集合的组成?
- endgame 发行策略是什么?
- 为什么不直接阻止新的 staker 加入?
- Staker 能否从减少的发行量中获利?真实/比例收益的相关性和影响是什么?
- 有些用户认为更多的收益更有趣,并且喜欢在他们的 ETH 上获得收益。为什么不倾向于此?
按顺序阅读答案是有益的,但它们仍然可以独立存在。
常见问题解答
以太坊为什么要减少发行量?
概述
在最基本的层面上,stake 参与度正在超出经济安全的要求,并且为人们做不必要的事情买单总是会带来负面影响。更具体地说,减少发行量有两个根本原因:
- 减少用户的成本,包括硬件成本、风险和机会成本、税收等。 通过维持当前的奖励曲线,以太坊迫使用户承担高于保护网络所需的成本。 减少发行量将通过消除可能高达每年超过 10 亿美元的隐性成本来改善福利。
- 从宏观层面改进以太坊。 如果每个人都进行 stake,一个实体或卡特尔可能会控制所有 ETH 的很大一部分。 这会降低安全性,因为社会层更难追究此类实体的责任。 流动性质押代币 (LST) 的潜在扩散也可能阻碍 ETH 作为无需信任的货币,助长垄断,并使以太坊成为一个不太理想的构建区块链。
答案现在将更仔细地研究这两个方面。
1. 降低成本提高福利
回顾图 1(此处有更多详细信息的示例),其中包含一个假设的未来供给曲线,以蓝色表示。 供给曲线表示在各种 staking 收益 y 下存入的 stake 数量 D。它捕捉了隐含的 staking 边际成本。 这意味着每个 ETH 持有者都根据他们分配给 staking 的成本高低沿着供给曲线定位,他们所需的回报率反映了该成本。相关成本包括硬件和其他资源、维护、技术知识的获取、流动性不足、对第三方的信任以及其他增加风险溢价的因素、各种机会成本、税收等。供给曲线之上的区域表示 staker 的剩余(他们实际获得的)。供给曲线之下的区域(供给曲线的积分)表示分配给 staking 的成本(边际 staker 不会以低于供给曲线的收益进行 staking)。
图 1. 在假设的未来供给曲线下,staking 的隐含成本(蓝色)和剩余(灰色)。 发行策略的改变将均衡从黑色方块转移到绿色圆圈。 只要协议保持安全和去中心化,成本降低(深蓝色)就会导致总体福利改善,而剩余的减少(深灰色)只是将一些效用从 staker 转移到每个人。
显示了两个奖励曲线,其中最大可提取价值 (MEV) 添加到 staking 收益中。 在本常见问题解答中,MEV 将为每年 30 万 ETH(接近过去几年的平均水平),并包括优先级费用。 通过维持黑色的当前奖励曲线,以太坊迫使用户承担高于保护网络所需的成本。 采用绿色奖励曲线消除了深蓝色区域代表的成本(约 450,000 ETH),从而提高了福利。 发行的 ETH 用于支付硬件费用、税收、降低的流动性和风险,用户在较低的收益下会选择回避这些费用。 有了绿色曲线,他们就可以这样做,并且每个人,包括剩余的 staker,都可以分享收益。 这通过减少新铸造的 ETH 为所有代币持有者创造了价值。 创建多少新 ETH 似乎很重要,这很奇怪。 但想象一下,如果所有 ETH 明天都转换为 10 ETH,那么总共有 12 亿 ETH,而不是 1.2 亿 ETH。 那么,每个 ETH 的价值将降低约 10 倍。 重要的是你持有的所有 ETH 的比例; 这将在后续答案中回到这个概念。 发行策略的改变还会导致剩余从 staker 转移到所有人,如较深的灰色区域所示。 事实上,ETH 之前使 staker 受益,因为它是从每个人那里获得的(以新铸造的 ETH 的形式),然后专门提供给他们。
通常将通过消除深蓝色区域实现的发行量减少与消除深灰色区域的发行量减少视为相同。 当没有明确强调那些停止 staking 的人随着发行量下降而降低的成本时,价值可能仅仅以真实/比例收益的形式从一类用户转移到另一类用户,从而获得收益或损失。 发行的代币在不同数量的 staker 中重新分配,没有在总体层面上创造任何新价值。 如果不将成本和剩余分开,福利增益可能会在翻译中丢失,特别是如果未通过评论不同均衡下所有用户的结果来暗示。 在后续答案中,将更仔细地研究不同的影响。
从“会计角度”来看,罚没风险或实际上会烧毁 stake 的任何错误,在总体协议层面上不太可能被认为是纯成本,并且税收本质上会在用户的剩余增加时增加用户的成本。 但是,捕捉低于供给曲线的成本作为不为 staker 产生任何剩余的发行量的一般原则对于理解 staking 经济学和福利非常有用。
当我们对用户施加不必要的成本时会发生什么 ? 如果他们被迫在承担作为 staker 的这些成本或在均衡下遭受更大的稀释之间进行选择,他们可能只会决定使用另一个区块链,那里的强制成本较低。 这当然会对代币持有者和在以太坊上构建的任何人产生负面影响。 以太坊在自由市场中运营,并且必须始终努力完善用户体验。
2. 宏观视角
真实成本核算还必须纳入宏观视角。 LST 超过关于其控制下的 stake 比例的关键阈值可能会损害共识机制。 此处来自区块空间的超额利润是卡特尔化的地层。 但是,如果每个人都被迫进行 stake,一个实体或实体卡特尔也可能控制总 ETH 的很大一部分——受到网络外部性的推动,例如 LST 的货币功能。 这些外部性是共识机制之外卡特尔化的地层。 受损的机构也位于上一层,即社会层。
The DAO 变得明显的是,如果受结果影响的总流通供应的比例足够大,那么社会层可能会对其对底层预期共识过程的承诺产生动摇。 LST 可能会在以太坊社会层的眼中发展到“ too big to fail”。 如果社区不能再有效地干预 51% 的攻击事件,那么 Vitalik 的警告系统和 Danny 的追索权可能无效。 Staking 变得如此普遍,以至于社会共识机制不堪重负。 这是 Vitalik 之前警告过的问题的一种特殊且某种程度上是相反的情况。
宏观视角也超越了共识。 如果一个或几个 LST 超越了以太坊生态系统中的货币,它们将会嵌入到每一层和应用程序中。 一个不由无需信任的资产驱动的经济可以说没有那么弹性,无论共识过程本身是否从未受到威胁。 为货币提供动力的应用程序将对使用货币的应用程序产生过大的影响,并且以太坊将成为一个不太理想的构建和开发区块链。
经济安全呢?更多的 stake 会使以太坊更安全,对吗?
没错,在达到某个点之前,更多的 stake 会使以太坊更安全。 但是,即使在达到这一点之前,添加另一个验证器所带来的安全性的边际增加为用户带来的效用也低于过度发行的大量缺点所带来的效用损失(请参阅前面的答案),这些缺点会对 ETH 代币的用户、构建者和持有者产生不利影响。 从长远来看,以太坊的经济安全将固有地与 ETH 保持其价值的能力相关联。 因此,在考虑经济安全时,全面的视角也很重要。 反思以太坊的早期阶段,当时 ETH 代币的价值远低于现在,这突显了这一点。 八年前,在 2016 年 5 月,Vitalik 详细阐述了以太坊可以在 30% 的 stake 参与度中保护和不能保护的价值。 当时,ETH 代币的市值大约比今天低 500 倍,因此以太坊可以提供的经济安全性受到限制。 将 stake 参与度从 30% 提高到 60% 只会将 1/3 的 stake(延迟最终确定能力 (delay finality) 的阈值)的价值从 7000 万美元提高到 1.4 亿美元。 这表明,一旦 stake 的比例上升到重要的水平以上,最终将是以太坊在世界经济中的角色,以及以太在以太坊经济中的角色,决定经济安全。
在最近的 AMA 中,Justin Drake 建议 1/4 的 stake 参与度(3000 万 ETH)是合适的。 Vitalik Buterin 赞同,但也补充了一个个人说明,认为 1/8(1500 万 ETH)也可以。 随着 stake 数量的增长,长期高经济安全的前景逐渐开始减弱。 有理由认为,与 9000 万 ETH 相比,以太坊在 20 年后的经济安全度更高,其奖励曲线使存款规模稳定在 3000 万 ETH 上——只要 staking 集合的组成保持可行。 超过某些限制,甚至短期安全也开始下降,这与围绕宏观视角的推理一致。 社会层可能会失去其中立性和可信度,成为针对来自主要 SSP 的攻击的最终仲裁者。 另一方面,如果用户没有被激励添加另一个验证器,而这会带来积极的效用,那么即使是长期安全性也会受到负面影响:短期安全性差且 stake 太少的区块链也不适合构建。
概述的考虑因素暗示了一个范围,在该范围内可以保持 stake 参与度。 没有单一的理想数量,因为以太坊可以根据安全性的普遍价格调整其安全支出,这可以通过奖励曲线来促进。 在 1500 万 ETH 时,staking 收益应该非常高,以确保足够的参与度。 当 stake 数量为 6000 万 ETH 时,staking 收益应该非常低,以阻止额外的 staking。 在 3000 万 ETH 的 stake 中,staking 收益可以设置在这些极端之间,达到可能形成均衡的水平。 请注意,总安全支出(发行量,Y_i)可能会保持相当固定,因为发行收益 y_i 会发生变化,因为当存入更多 stake 时,发行的代币将分配给更多的 staker,从而降低收益。 这种关系由等式 Y_i=y_iD 表示。 经济安全也在此处讨论。
近期内理想的发行量减少是多少?
概述
理想的做法是采用位于下图 2-4 中的黄色区域内的奖励曲线。 可以使用具有 tempered issuance 的奖励曲线(随着 stake 数量的增加而缓慢下降)来实现,如绿色示例所示,或者使用上限 issuance 的奖励曲线来实现,如粉色示例所示。 低于黄色区域的奖励曲线会使 MEV 的影响相当麻烦,因为区块提议权将带来比 attestation 相对更多的价值,并且此时也可能没有必要。 高于黄色区域的奖励曲线可能相对于改变发行策略可能带来的潜在棘手的治理过程而言不够有影响力。
MEV 的影响
对奖励曲线的任何更改都应考虑 MEV。 如果没有同时烧毁 MEV,则强制执行少量 stake 是不可取的,如最近的一篇文章和以下答案中所探讨的那样。 如果发行收益减少以严格执行在高 MEV 存在下的均衡,则区块提议权可能是剩余的唯一收入来源。 这将显着增加非池化 staker 的 staking 收益的相对标准偏差,从而使 solo staker 处于不利地位。 在某些时候,staker 可能会停止证明。 当发行收益变得过低时,需要对共识机制进行额外更改才能保持微观激励。 在我看来,每 epoch 收取的 staking 费用似乎是最佳选择,并且将提升“ 激励不变性”。 然后,即使在较低的正发行收益下,非池化 staker 也需要在每个 epoch 损失 ETH,希望他们可能会被分配到提议区块。 例如,在奖励曲线处于黄色区域的下边缘或略低于黄色区域的情况下,一个简单的解决方案是增加对错过证明的惩罚。
合理的范围
那么,目前可以考虑哪些更温和的选择? 图 2 显示了目前合理的黄颜色范围。 低于此范围,在当前的 MEV 水平下,区块提议将产生超过一半的奖励,这可能是一个令人不安的高水平。 高于此范围,更改相对较小,并且更改奖励曲线的潜在棘手的治理过程可能不值得。 还有一些选项可以在大量 stake 时进一步降低 staking 收益,这些选项不能完全排除,此处讨论。
图 2. 通过具有 tempered issuance 的奖励曲线(绿色)或上限 issuance 的奖励曲线(粉色)实现的合理发行范围,以黄色表示。
具有 tempered issuance 的奖励曲线(绿色)
黑色的当前奖励曲线遵循发行收益的等式 y_i = cF/\sqrt{D},其中常数 c\approx2.6,基本奖励因子设置为 F=64。 年度发行量始终为 Y_i=y_iD。 通过除以 1+D/k 创建了绿色的 具有 tempered issuance 的奖励曲线,因此:
y_i = \frac{cF}{\sqrt{D}(1+D/k)},
其中 k 设置为 2^{25}。 变量 k 定义了峰值发行时的参与度,这也变成了发行量减半的点,以下方的十字表示,约为 3360 万 ETH。 虚线绿色奖励曲线对计算进行了细微的更改,在计算新项时,从 D 中减去一个固定的常数 k_2(最小值为 0)。 此处的常数设置为 k_2=2^{23}。 这样做的目的是提供更强的保证,保证有足够的 stake 数量,从而保证安全性。 虽然这不太可能需要,但它仍然可以使找到变更协议的治理过程更容易。 还可以通过使用更高阶的奖励曲线来实现类似的效果。
具有上限 issuance 的奖励曲线(粉色)
粉色表示具有上限 issuance 的奖励曲线(此处有较短的撰写)。 当发行量偏离当前的奖励曲线并趋于平稳时,上限 D_c 定义 stake 参与度。 寻求范围内的最低设置是 D_c=2^{23} (840 万 ETH),用点曲线表示,最高设置是 D_c=2^{24} (1680 万 ETH),用实线表示。 一个有趣的细节是,Vitalik Buterin 在 2021 年 3 月提出的 活跃验证器上限和轮换提议对发行量的影响与应用 D_c=2^{24} 时的影响相同。 因此,该奖励曲线的一个好处是其悠久的历史,可能是有节制地增长积极参与 stake 的第一个严肃提议。 读者可能会发现该帖子上的评论部分很有趣,其中包含关于以太坊流通供应均衡、针对参与率和可变验证器余额的早期想法。 虚线粉色曲线对应于可行的选项 $D_c=15$M ETH。 中点 2^{23}\sqrt{2} 可能也很有趣(未绘制)。
Staking 收益和展望
图 3 显示了 staking 收益 y=y_i+y_v,包括在每年 30 万 ETH MEV 当前水平下的 MEV 收益 y_v,适用于一些先前概述的奖励曲线(保留颜色和线型)。 蓝色是与图 1 中相同的假设未来供给曲线。 它旨在说明几年后供给曲线可能是什么样子,以此来了解均衡是如何形成的。 在经过几年后,淡蓝色线可能是供给曲线和与 stake 相关的成本进一步下降。 两种奖励曲线之间均衡收益的差异将取决于供给曲线的斜率,并且如图所示,可能没有那么显着,此处为 0.5%。
图 3. 来自概述的奖励曲线的 staking 收益,包括每年 30 万 ETH 的 MEV。 两条假设的供给曲线以蓝色表示。
图 4 仅显示发行收益,没有来自 MEV 的奖励。 如果成功实施 MEV 销毁(例如,1,2,3),则 staking 收益可能会接近这些水平。 但是,MEV 销毁处于非常早期的研究阶段,不能保证成功,并且 MEV 的某些部分(例如共识层预确认)可能永远不会被销毁。 该图说明,经过几年后,由于供给曲线的持续下降,均衡的 staking 收益也可能会降低。 在这种假设情况下,综合影响将 staking 收益降低至 1.76%,但仍在当前奖励曲线的均衡收益的 0.5% 以内。
图 4. 概述的奖励曲线下的发行收益 y_i。 如果所有 MEV 都已成功销毁,那么这也是 staking 收益,这种情况可能不会实现。 两条假设的供给曲线以蓝色表示。
可以注意到,来自 MEV 销毁的降低的 staking 收益使在理想 stake 数量下的均衡非常有可能,即使供给曲线继续下降也是如此。 因此,采用类似于虚线绿色奖励曲线的东西,然后稍后进行 MEV 销毁,可以使以太坊达到一个 stake 数量受到限制并保持在 6000 万 ETH 以下的阶段,可能更接近 3000 万 ETH。 这并不意味着该奖励曲线必须保持不变。 但是,奖励曲线应该给我们足够的时间来继续讨论“endgame”发行策略(请参阅此答案),而不必担心 stake 数量会高得令人衰弱。
为什么不使用像 EIP-1559 这样的机制动态调整收益,以保证某个固定的目标参与度水平?
概述
一个常见的建议是,以太坊应该使用像 EIP-1559 这样的机制来自动调整收益,从而确保 stake 参与度保持在某个特定的目标水平。 允许市场设置发行收益似乎更中立,从而取消了开发人员的控制权。 当然,这只是将问题转移到定义一个特定合适的 stake 数量。 更糟糕的是,它限制了以太坊购买同等数量的安全性,而不管其成本如何。 可以说,没有一个特定的合适的 stake 数量,因为安全性的价格(均衡发行水平)也很重要。
正如先前讨论的,添加另一个验证器所带来的安全性的边际增加会随着 stake 数量的增加而降低效用。 在某些时候,过度发行的效用损失会大于更多安全性带来的效用收益。 显然,这一点也取决于安全性的成本。 目标参与水平的另一个担忧是,它会激励 staker 不鼓励攻击以太坊以提高发行量,在一个版本中作为联盟运作。 尝试纠正这些缺陷最终将重新创建某种形式的奖励曲线,因为它在许多方面都是一个更复杂的解决方案。
固定目标参与水平是具有低于标准预算的垂直奖励曲线
当收益动态调整以强制执行某个特定的目标参与水平时,该机制从长远来看的行为类似于垂直奖励曲线。 任何此类机制当然都会逐渐适应,以避免供给曲线的微小变化导致收益的过大变化,但均衡最终会回到供给曲线与垂直“动态”奖励曲线相交的点。 图 5 中以洋红色说明了两个这样的奖励曲线,一个目标设置为 3000 万 ETH 的 stake,另一个目标设置为 6000 万 ETH 的 stake。 该图假定每年有 30 万 ETH 的 MEV。另一个答案中介绍的常规奖励曲线“Endgame (3)”改为以紫色显示。
图 5. 在蓝色表示的各种供给曲线下,当使用固定目标参与水平(洋红色)、具有 cut issuance 的奖励曲线(紫色)或当前的奖励曲线(黑色)时的均衡。 绿色圆圈表示理想的结果,红色叉号表示不良的结果,黄色三角形表示介于两者之间的结果。 如红色叉号所示,固定目标不利于适当的预算。
图中显示了三条假设的供给曲线(以蓝色显示),旨在说明在截然不同的情况下结果会是什么。 在高供给曲线下的 3000 万目标下,均衡的 staking 收益为 2.87%; 这是在 MEV 存在下理想的结果,用绿色圆圈标记。 在概述的中等供给曲线下,均衡的 staking 收益改为 1.87%。 这可能会被认为是稍微有问题的,因为 MEV 将构成总 staking 奖励的 53.5%。 因此,区块提议在当前的共识规范下会带来大约 59.3% 的所有奖励,因此均衡用黄色三角形标记,表示中等结果。 然而,在我看来,它非常接近被归类为绿色圆圈。 在低供给曲线下的均衡,staking 收益为 0.5%,用红色叉号标记,表示不良性。 由于 MEV 收益为 1%,因此这种均衡发生在负发行收益下。 然后,非池化 staker(例如,大多数 solo staker)必须在每个 epoch 损失资金,希望最终被分配到提议区块。 在高供给曲线下的 6000 万目标下,均衡状态形成于 4.6% 的质押收益率。这是非常不理想的。在这种情况下,以太坊每年将发行 245 万个 ETH,而 3000 万个 ETH 的均衡发行量为 0.56 百万个 ETH 就足够了。当然,缺点是以太坊让其用户承担了不必要的成本。对于用户而言,这表现为被迫承担其中一些成本作为质押者,或者看到他们的储蓄被稀释侵蚀。由于同样的原因,中等供给曲线的均衡也是不理想的。然而,低供给曲线的均衡似乎可以接受,质押收益率为 1.11%。MEV 有点高,占奖励的 45%,而且实际上提议者获得了预期质押收益率的 51.8%。然而,为了防止在低供给曲线下质押数量增长过高,这似乎是可以接受的,因为 6000 万 ETH 已经高得令人不悦。
动态奖励曲线和特定目标的问题在于,相关的垂直形状可能导致不理想的质押均衡。读者会注意到,通过使用紫色奖励曲线(表示为“Endgame (3)”),在所有三个供给曲线下都达到了可接受的均衡,如绿色圆圈所示。如果供给曲线较高,则可以实现质押数量较低的均衡,从而确保以太坊用户的成本不会增长过大。如果供给曲线较低,则允许质押数量增长,以确保为质押者提供合理的发行收益率。这还使以太坊能够确保质押集的有效组成。
供给曲线的未来水平将永远是未知的,因此必须设计奖励曲线(需求曲线),以便在任何合理的情况下都能产生可接受的结果。在某种程度上,理想的奖励曲线可以理解为扩张路径,它优化了潜在供给曲线上的收益率和质押参与度之间的关系,如后续答案中所述。当前的奖励曲线以黑色显示,并且如所指示,将产生过多的发行量(用户成本),同时还会导致在较低的供给曲线下质押数量过高。
以太坊目前正在研究 MEV 销毁。这将缓解对导致 MEV 比例过高的特定均衡的一些担忧。图 6 显示了在完全 MEV 销毁下的结果。
图 6. 在使用固定目标参与度水平(品红色)、采用削减发行的奖励曲线(紫色)或当前奖励曲线(黑色)时,MEV 销毁下各种供给曲线的均衡(蓝色)。绿色圆圈代表理想结果,红色叉号代表不良结果,黄色三角形代表介于两者之间的结果。
如果不存在 MEV,则在质押 3000 万 ETH 时,较低质押收益率下的均衡问题较少。例如,非集中质押者每个 epoch 都会收到正奖励。低供给曲线下的均衡仍然用黄色三角形标记。可以公平地用绿色圆圈标记它,但在我看来,我们可能希望在这些供给曲线下稍微扩大质押数量。这会带来更高的均衡收益率,并将更好地保证质押集的可行组成。一种理解方式是,奖励曲线有助于吸收所有具有低保留收益率的委托质押者,以确保收益率对于单独质押而言仍然可行。
下图 7 绘制了年度总奖励(此处也对应于总发行量,因为在本示例中 MEV 销毁已到位)。在高供给曲线和 6000 万 ETH 的固定目标下,过高的发行量非常成问题。同样,在当前奖励曲线下,低供给曲线下的高发行量也令人担忧。请注意,当前奖励曲线的真正成问题的结果发生在低供给曲线下,因为它旨在随着质押数量的增加而增加发行量。
图 7. 在使用固定目标参与度水平(品红色)、采用削减发行的奖励曲线(紫色)或当前奖励曲线(黑色)时,MEV 销毁下各种供给曲线的年度发行量(蓝色)。绿色圆圈代表理想结果,红色叉号代表不良结果,黄色三角形代表介于两者之间的结果。如果供给曲线较高,则 6000 万 ETH 的固定目标(品红色)将导致过多的发行量。
固定目标参与度水平可能会怂恿质押者攻击以太坊
上一节确定了不为以太坊的安全支出附加适当预算机制的缺点。这可能导致以太坊为安全性支付过多,或者支付过少,以至于单独质押者不必要地被赶出去。有些人可能认为对单独质押的担忧被夸大了,并且认为特定目标的好处超过了这一点,因为以太坊至少会拥有社区认为适当的特定参与度水平。然而,固定目标的问题有点更深。质押者需要在监听器-发言者故障等效性下达成共识,这为劝退攻击开辟了途径。该协议无法确定谁应该对未成功交付的共识消息负责。因此,攻击者可以恶意地针对诚实的共识参与者,以剥夺他们的奖励,随后随着他们离开并且质押收益率增加而获利。甚至存在各种少数人劝退攻击的途径。
对于适应速度相对较快的固定目标参与度水平,“p_i-弹性”变为无穷大。然后,劝退攻击的动机被最大化;必须离开的质押量更少才能提高收益率。一个相关的概念是卡特尔攻击,包括 SSP 合作以试图减少质押数量,也可能在他们之间进行。当发行量随着质押数量的减少而增加时 (p_i>1),所有质押者都可以尝试同意减少他们的质押,并且每个人都会变得更好(只要阻止或劝退新进入者)。这种框架可以为说服社会层不要干预质押卡特尔试图抑制以太坊的无需许可性,利用劝退攻击提供合适的背景。
不应过分夸大劝退攻击的重要性,但是当可以轻松实现更安全的设计时,不必要地为它们敞开大门。尤其引人注目的是,在严格目标下,通过审查攻击共识可以产生本质上是无限金钱漏洞,而不会破坏有效性。
纠正概述的缺陷会重新创建一个次优的奖励曲线
为了防止质押者将共识机制变成印钞机,该协议当然可以施加一些最大收益率,超过该收益率,不再认为有必要进一步增加(除了依靠社会层和社会干预的威胁)。为了安全起见,发行政策还可以定义一个下限,以便质押者始终获得一些收益,从而确保质押集的可行组成。图 8 绘制了这种新的假设更新的固定目标奖励曲线(再次忽略时间分量)。上限设置为 5%,下限设置为 0.25%。
图 8. 具有上下限的固定目标参与度水平,试图纠正图 5-7 所示设计的某些问题。但是,奖励曲线仍然是更好的解决方案。
该机制现在可以防止无限金钱漏洞,并为质押者提供至少一些有保障的收益。但是,它仍然存在缺陷,预算编制不当。对于曲线的垂直部分,劝退攻击和卡特尔攻击的动机仍然不必要地明显。固定下限和上限应该具有奖励曲线的平滑特征,随着效用函数的变化而逐渐增加或减少。
概述的缺陷并不意味着动态方法没有价值;可以将它与奖励曲线结合起来。这个想法是允许奖励曲线在更长的时间尺度上漂移/弯曲,最终受到单独的目标奖励曲线的影响。在关于质押经济学 endgame 的答案中探讨了这种“ 时间-数量政策”。
发行量减少将如何影响质押集的组成?
概述
这取决于诸如单独质押者和委托质押者之类的相关群体对低质押收益率和高变异性的敏感程度。一个担忧是单独质押者在低收益率下的不利规模经济。与此同时,委托质押者在信任第三方持有其 ETH 时会面临独特的风险,并且如果收益率过低,也可能会犹豫不决地进行质押。此外,随着质押数量的增长,委托质押会变得相对更有利。因此,需要考虑多种相互冲突的经济力量。解决这个复杂主题的一种方法是比较尝试捕捉单独质押者和委托质押者在不同收益率下质押意愿的分布,如下面的图 11 所示。
重要的是要理解发行政策的概率性质,以及该设计最终试图优化任何场景(例如,较低或较高的供给曲线)下的结果。如另一个答案中所述,在这种情况下,合适的奖励曲线可以理解为跨潜在供给曲线的扩展路径,该路径以最佳方式平衡权衡。其中一项权衡是质押集的均衡组成。考虑到这一观点和潜在的担忧,3000 万 ETH 的均衡可能是理想的,但仍然不会受到经济上限的强制执行。在特别低的供应曲线下,可以允许质押数量增加。因此,必须最终在两个维度上分析和优化质押集的组成,即发行水平和质押数量。
单独质押者的变异性
如果发行受到限制,则奖励的更大部分将来自 REV,因此质押奖励的相对变异性将增加。这会对单独质押者产生不利影响,因为他们无法毫不费力地依靠池来平滑变异性。先前关于发行水平属性的撰写中提供了对变异性如何影响单独质押者的回顾。似乎可以合理地假设,质押者可能对在较低质押收益率下的方差更敏感——相对变异性很重要。在发行收益率为负但质押收益率(包括 REV)为正的均衡状态下,这一点当然是正确的——例如,在实行经济上限时(1、2)。然后,不合并其执行层奖励的单独质押者将需要每个 epoch 损失 ETH,以期被分配提议一个区块。由于 MEV 收益在质押者之间共享,因此它会随着质押数量的减少而增加,因此,经济上限设置得越低,这种均衡就越有可能出现,因为 MEV 收益仍然可以本身成为足够的激励。相对变异性是在 MEV 销毁到位之前,追求先前答案中讨论的更温和的奖励曲线的原因之一。这并不意味着之后会强制执行低经济上限,只是说一旦 MEV 销毁到位,它就更可行了。
均衡收益率和单独质押者的比例
以太坊希望保留单独质押者,至少在衡量为所有质押者的比例时。减少发行水平的预期结果是,与未减少发行量的情况相比,委托质押者和单独质押者都会质押更少的 ETH(1、2)。一个担忧是,是否存在低于该值的质押收益率,尤其是在单独质押者会由于与单独质押相关的相对较高的固定成本而减少的情况下。
例如,以图 3作为起点。尚不清楚在质押约 3600 万 ETH 和质押收益率为 2.44%(采用缓和发行量的绿色虚线奖励曲线)的假设均衡状态下,单独质押者的比例是否低于在质押约 5000 万 ETH 和质押收益率为 2.94%(黑色当前奖励曲线)时。如果单独质押者在低于 2.6% 的收益率以下大规模离开,那么在质押 3600 万 ETH 时的质押收益率为 2.44% 将给出比质押 5000 万 ETH 时的收益率为 2.94% 的比例更低的比例。这当然是需要认真对待的事情。规模经济很难在去中心化的区块链中设计。
但是,也有一些论据表明,更严格的奖励曲线可能会提供更高或至少相似比例的单独质押者:
- 占主导地位的 SSP 在质押数量较高的情况下具有更好的规模经济,从而增加了它们相对于单独质押者的成本优势。
- 同样,货币功能的正向网络外部性随着质押数量的增加而增长,并且随之而来的是占主导地位的 LST 发行 SSP 的竞争优势。
- 此外,如果其他人都使用 LST,并且期望社会层在失败的情况下会动摇其对预期共识过程的承诺,那么与 LST 相关的委托人-代理人问题可能看起来风险较小。
- 随着收益率下降,风险很可能会比单独质押者更早地阻止委托质押者。例如,如果足够大的潜在委托人子集认为他们希望持有的 LST 在一年内有 1% 的失败风险,那么有利的规模经济或流动性可能不足以成为竞争优势。自我托管无疑对相当一部分 ETH 代币持有人来说是重要的;在评估质押供应方时不应忽视这一因素。
- 以类似的主题,如果收益率变为负值,则仍然存在单独质押的利他动机。委托质押者要么需要承担损失,要么面临不利选择。补贴委托人的 SSP 将在期望未来利润的情况下这样做,这可以通过垄断某些关键功能或更糟糕的是,通过攻击共识来获得。从重新质押中获利的 SSP 也可以同样利用非质押的 ETH 获利。
- 拥有足够的 ETH 和单独质押的技术能力的代币持有人不一定很丰富,这意味着单独质押数量的软上限。可以认为,如果这个池或多或少已经耗尽,那么随着供应曲线下降并且 D 在当前政策下增加,相对少数新的质押者将是单独质押者。尽管如此,关于这个特定的论点,应该记住,如果大幅降低收益率以阻止 D 的增加,则不能保证长期保持更大比例的单独质押者。这最终取决于它们的保留收益率的更精细分布,如下一小节所述。
发行政策应侧重于长期目标,而不应依赖短期补救措施。如果期望它们会停止,这也与目前相当有价值的单独质押空投有关。然而,以太坊不断发展的共识机制在十年内可能会有所不同,对质押有不同的要求——甚至可能存在不同类别的验证者(1、2)——因此不能完全忽略当前和近期未来的情况。例如,必须承认,如果收益率下降,任何单独质押空投的影响都将成倍增加。例如,如果它们的预期价值为每年 1%,并且质押收益率从 4% 下降到 1%,那么空投将使单独质押者的收入比委托质押者高 25%,而达到 100%。
还可以向第四个要点添加一个额外的细微差别:一些单独质押者质押的数量远远超过 32 ETH,并且他们可能更能抵抗低收益率。最后请注意,不拥有自己硬件的单独质押者仍然可以享受一些外部规模经济;相反,家庭质押者会直接受到硬件成本的影响。
从根本上说,推测是不同类别的质押者之间的保留收益率的相对分布可能不同。这会导致在不同的发行政策下,单独质押者的比例有所不同。但是,在这种情况下,一种政策是否优于另一种政策尚无法确定,并且可能在未来十年内也会有所不同。
保留收益率的相对分布
本小节将通过可视化不同类别质押者之间的一些假设的保留收益率分布来解释上一段的推测。自然,这些分布来自一些基本的函数,这些函数捕获了供应质押的意愿,而这些函数最终取决于寻求 ETH 资产敞口的人的组成以及他们如何评估与质押相关的各种成本。我将在稍后介绍此类模型。这些可视化将仅根据上一小节中提出的想法来说明分布的样子,而无需量化实际的潜在经济力量。
“保留收益率”的概念是从劳动经济学中借鉴的,其中保留工资会影响跨工资(劳动供给曲线)的劳动供应量。质押经济学和劳动经济学有一些相似之处;毕竟,质押是为维持共识过程所做的工作,而质押者(就像工人一样)在某些情况下可以组成卡特尔(即,工会/卡特尔攻击),如先前答案中所述。劳动者对其闲暇时间的估值在某种程度上对应于代币持有者附加到非质押 ETH 的溢价。但是应该提到的是,这里的“保留收益率”适用于“潜在”的代币持有者。目的是捕捉某些代币将被质押的特定收益率,但必须认识到,由于情况的变化,实际的代币持有者可能会发生变化。
假设指定的保留收益率也适用于在考虑其他质押者的保留收益率时形成的均衡状态,并且质押不会跨质押收益率切换质押方式。另请注意,保留收益率表示质押收益率必须是多少,而不是质押者的利润,因为还存在成本/费用。该示例旨在捕捉假设的几年后的分布可能是什么样子,假设有效的 MEV 销毁已经到位,并且不幸的是,对单独质押者的空投已变得不那么普遍。
说明保留收益率的假设分布
图 9 中的虚线显示了单独质押者的假设保留收益率分布,x 轴为质押收益率。据推测,没有多少质押者具有零或负保留收益率。即使共识机制没有提供直接的货币激励(质押收益率为 0),也可能有极少数人倾向于进行质押,也可能是为了防御或攻击网络。但是这些激励措施不是以太坊希望依赖的。随着质押收益率的上升,每次边际增加都会吸引更大一部分 ETH 代币持有者作为单独质押者。随着整体质押参与率的提高,潜在的单独质押者池逐渐耗尽,曲线达到峰值(此处约为 2%),并且收益率的提高最终也不会吸引许多新的质押者。
图 9. 单独质押者之间保留收益率的假设分布。
相反,图 10 中的虚线显示了潜在的委托质押者之间保留收益率的分布。该分布通常可能具有更正的偏度。这个想法是(稍微简化)最后四分之一的质押者倾向于流动性,并且可能没有单独质押的技术能力,而有利的规模经济在较低收益率下带来了更显着的增长。先前说明的单独质押者的假设分布也包含在该图中,但是它们的数量相对较少,因此很难比较形状。
图 10. 委托质押者之间保留收益率的假设分布(虚线)。还包括来自先前图 9 的单独质押者的分布(点线)。
为了更容易进行比较,图 11 显示了两个分布,这些分布都已标准化以表示所有 ETH 的相等份额。尽管如此,请记住,这些曲线仅试图说明上一小节中提出的想法,因此是假设性的。但是另一方面,即使在更深思熟虑的模型下,此警告也可能始终适用。分布的相对比较捕获了这样一种概念,即由于不利选择和较不明显的利他动机的可能性,较小比例的委托质押者愿意以负收益率进行质押。但是,由于委托质押的有利规模经济,随着收益率变为正值,分布可能会比单独质押者的分布更快地上升。随着收益率的进一步提高,单独质押发挥作用,但随后会减少,因为最后一部分质押者不愿意放弃流动性或在技术上无法单独质押。因此,单独质押者的比例可能会间歇性地变化。
图 11. 单独质押者和委托质押者的保留收益率的假设分布,已标准化以表示所有 ETH 的相等份额。
回顾了两个假设分布后,现在是时候回顾一下在这些分布下,单独质押者的比例如何随着质押收益率的提高而演变。然后计算累积分布,看到质押者将在高于其保留收益率的任何收益率下进行质押。这些如图 12 所示。理解这些图的一种方法是将初始分布视为概率密度函数 (PDF),然后计算其对应的累积分布函数 (CDF)。
图 12. 单独质押者(点线)、委托质押者(虚线)和总计(完整)的保留收益率的假设累积分布。
单独质押者的比例仅仅是单独质押 CDF 除以总 CDF,如图 13 所示。这里没有断言会实现这个特定结果,但它可以说明辩论中存在的各种概念。在负收益率下,单独质押者的比例较高,但是由于规模经济,在低质押收益率下会出现一些低谷。如果委托质押者的指定风险溢价比单独质押者的固定成本结构更分散,则可能会出现这种情况。更高发行水平的支持者会建议这个低谷存在并且很明显(在删除单独质押空投时),但是除了规模经济之外,还有许多细微差别需要考虑,如先前所述。无论如何,尚不清楚这种效应是否一定很重要。
图 13. 跨质押收益率的单独质押者的假设比例。
由于供给曲线的每个点都代表边际质押者的保留收益率,因此保留收益率的累积分布实际上对应于供给曲线。为了清楚起见,只需翻转图 12 的轴,使 y 轴为收益率,x 轴为质押。然后,以更常见的形式显示供给曲线,如图 14 中的蓝色所示。包括了两个没有 MEV 的奖励曲线——来自先前的答案的黑色当前奖励曲线和具有上限发行量 D_c = 15M ETH 的温和奖励曲线。两个假设的均衡由正方形表示,位于总供给曲线和这些奖励曲线的交点处。单独质押者和委托质押者的参与率仅在从均衡延伸的水平线上找到,在该线与相关的集合供给曲线相交的点(圆形)。
图 14. 保留收益率的累积分布,此处以蓝色表示为供给曲线,轴从图 12 翻转。还指示了委托质押者和单独质押者的集合供给曲线。每个类别的质押参与度(圆形)位于从均衡延伸的水平线上(正方形)。
请注意,此处提出的假设分布仅给出一条特定的供给曲线。在另一条较低的供给曲线下,这些分布可能会被压缩,从而使许多特征(例如,向有利于委托质押的过渡)以较低的收益率出现。我一直在研究一个复杂的概率模型,试图统一这些考虑因素,并且希望在一段时间内展示它。该主题肯定也会受到其他研究人员的进一步关注(例如,1、2、3)。
均衡收益率和质押集更广泛的组成
发行水平与 SSP 多样性之间的关系也需要权衡规模经济与诸如货币功能的正向网络外部性等因素权衡。提供超过 3000 万 ETH 的正收益率有助于缓解人们的担忧,即具有结构优势(例如中心化交易所 (CEX))的主要 SSP(可能利用一些假设的质押 ETF)会将其质押比例提高到关键水平。与此同时,不应过分强调围绕此类实体的中心化风险,而应将其置于其他风险情景之上。如今,已经有 SSP 通过利用链上的网络外部性,表面上放弃利润以追求垄断,从而获得至关重要的质押比例。这种结构性优势也可能会随着发行的增加而增长,并且必须将原生 ETH 可能相对于一个 LST 而言处于少数地位之前对其进行抑制,这被认为是社区的净收益。在权衡这些权衡时,始终强制执行任何结果(无论是非常低的还是非常高的质押数量)的发行水平似乎并不理想。 每个SSP都在争取特定的市场份额,除了运行质押节点的成本外,还会产生独特的成本,范围从合规到软件不等。实际上,中心化交易所(CEX)在某种程度上对它们的客户(即委托人)拥有某种本地垄断,并且使费用与任何链上选项保持竞争力的机会成本可能非常高,以至于它并不代表利润最大化的策略。 显而易见的是,对委托权益的竞争将在不同的市场领域展开,而完全竞争并非一个合理的假设。 如果运营节点的成本相对于 SSP 从运行节点中获得的收入而言并非过高,那么委托人之间的偏好和情况的多样性将在塑造质押集合的构成中发挥核心作用。 因此,只有在少量权益下收益接近 0 或负数时,这种担忧才有效。 没有 SSP 能够在例如 3000 万 ETH 的质押量下,以 2% 的均衡质押收益合理地击败所有其他 SSP。
最终状态的发行策略是什么?
概述
最终状态的某些部分已经达成了相当广泛的共识。 首先,以太坊应该过渡到在奖励曲线的等式中使用 d(在本文中称为存款比率或权益参与率)而不是 D(存款规模或权益数量)。 这可以通过简单地将奖励曲线公式中的 D 替换为 d 来完成 (1, 2),并在交换时通过包含流通供应量进行标准化,一旦流通供应量开始在共识层被追踪。 这种转变的主要原因是,在长期质押均衡状态下,适应 D 而不是 d 的奖励曲线最终也受到流通供应均衡的影响,因为流通供应量将漂移以平衡供应、需求和协议收入。
其次,以太坊应该追求 MEV 销毁。 正如之前的回答所解释的 (1, 2),这将减少相对可变性,并且是在不引起对非矿池质押者过多担忧的情况下大幅降低质押收益的先决条件。 由于答案很快转向减少发行,因此必须记住,如果内生质押收益(MEV + 发行 + 空投)为负,则没有直接的财务动机进行质押。 因此,在吸引足够数量的权益的负发行下的均衡状态仍然应该涉及正的预期内生收益。 一个担忧是,MEV 的可变性涉及非矿池质押者在等待被分配到特殊职责时,每个 epoch 都要承担小的损失(请注意,空投的可变性不能通过矿池来解决)。 但 MEV 销毁还有许多其他原因,正如 Francesco、Justin 以及 Mike、Toni 和 Justin 所探讨的那样。
当谈到发行水平时,最终状态目前是一个争论的主题,但实际上所有方面都涉及发行量的减少。 这些选项大致可以分为五个不同的类别:
- 什么都不做;一个必须始终成为对话一部分的替代方案,但假设质押成本继续下降且权益数量进一步增加,那么这个替代方案的吸引力越来越小。
- 缓和发行;但要达到在 MEV 存在下也完全足够的水平。
- 削减发行;位于(2)和(4)之间的选项。 不会建立经济上限,而是通过大幅降低收益来让大量权益变得难以置信。
- 经济上限,通过在一些理想的权益数量下,让质押收益变为负无穷大。
- 时间-数量策略;其中允许奖励曲线响应于供应曲线的变化而缓慢改变/弯曲。
在这些选项中,(2)在我看来,在这一点上变得越来越理想。 然后有一个从(3)到(4)的滑动比例,更严格的奖励曲线因其能够提供关于权益数量的保证而具有优势,但同时一些限制性设置也需要更多的审议。 经济上限(4)可能具有优点,理想情况下是在 MEV 销毁之后,但在我看来,不要在过低的权益数量下进行。 将说明一些例子。 类别(5)尚未受到太多研究,并将更深入地介绍。 答案现在将简要回顾优化问题的哲学基础,然后仔细研究这五个类别中的每一个。
优化问题的哲学基础
奖励曲线本质上是一种尝试在所有已知的权衡(长期和短期的经济安全性、低成本、可行的质押集合构成、奖励可变性等)之间进行优化,从而确保在任何供应曲线下都能实现效用最大化的均衡。 因此,理解这个问题的一种方式是,每个假设的供应曲线(低和高)都有一个最佳均衡,奖励曲线应该在这个点上与每个供应曲线相交。
在经济学中,扩张路径连接了跨输出水平的最佳投入组合,而收入扩张路径选择了跨收入的最佳消费束。 合适的奖励曲线是扩张路径,它可以优化与高/低收益和权益参与相关的,所有已知的在潜在供应曲线上的权衡。图 5-8 在之前的回答中说明了在三个不同水平的供应曲线下的概念,其中可以使用来自最终状态(3)的奖励曲线在所有三个曲线下找到最佳均衡。
正如 Vitalik 在类似背景下所表述的那样:如果奖励曲线的设计使得某些特定的均衡成为可能,那么首先应该认为该均衡是可以接受的。 特别是,理想情况下,它应该是当前供应曲线的最佳均衡。 但还必须注意的是,不仅供应曲线的水平,而且供应曲线的形状也很重要。 原因是该形状将影响在优化时可以用哪些替代方案来替代特定的均衡点。 Caspar 和 Ansgar 的图中 30M 和 120M ETH 之间的几乎水平的供应曲线,与本文中几乎垂直向上倾斜到 120M ETH 的供应曲线之间存在差异。 在前一种情况下,在 30M ETH 时设置负收益似乎是一个更自然的解决方案,因为无论供应曲线是较低还是较高,在低权益数量下的经济上限可能对单人质押者来说无关紧要。
1. 什么都不做
当权益数量保持在合理接近 30M ETH(权益的 1/4)时,此选项仍然有效,之前已将其讨论为潜在的限制。 更改去中心化区块链的发行策略存在一个切换障碍。 如果切换发生在过于接近之前讨论的限制的情况下,那么潜在的不满情绪会更高。 但正如在另一个答案中提到的那样,似乎有理由假设目前 32M ETH 的权益数量不会长期保持不变,因为质押成本(广义上定义)会下降。 一个可以很好地符合以 2 的幂运算的概念的阈值是 2^{25} ETH,对应于 33.6M ETH。 一旦以保持不变的情况下超过这个阈值(或者在超过的道路上),那么做一些事情似乎对我来说是一个更好的选择。
不幸的是,对于质押的过度激励(超过了安全性所需的激励)随着时间的推移可能会变成有害的补贴。 在应用层围绕过度的质押收益构建的场景中,以太坊经济可以说不会有适当的无需信任的基础,正如之前讨论的那样。
在决定 “不做任何事情” 和 “做一些事情” 之前,需要跟踪的一件事是 MEV 销毁的进展。 减少发行不应与纳入 MEV 销毁在同一个硬分叉中进行。 如果 MEV 销毁非常接近准备就绪,那么在某些情况下可以对此进行考虑。 但 MEV 销毁仍处于早期研究阶段。 因此,一种方法是在 MEV 销毁前一两年内,立即适度减少发行,然后让 MEV 销毁在质押收益中再减少一部分。
2. 缓和发行
这个选项在之前的回答中提出。 总而言之,它代表了一种 “安全” 的发行减少,不会增加非矿池质押者的相对可变性,从而为整个范围内的质押者提供相关的质押收益。 该选项提供了足够大的发行减少量,使得相关的治理过程值得进行 —— 并且足够小,可以使该过程可能更容易。 该选项仍然会大大缓解权益数量的增长。 结合 MEV 销毁,它可以合理地构成最终状态发行策略,这意味着权益数量保持接近 30M ETH 并且牢固地低于 60M ETH。 但是,这并不意味着(2)必须是最终状态。 在更高的权益数量下进一步减少发行,如(3)和(4)中所示,在 MEV 销毁后似乎是一个合理的选择。 但是,进一步超过(2),例如到(4),则将需要单独讨论。 有一个简单的 “开启开关” 可以用于这种转换,如相关的小节中所讨论的那样。
3. 削减发行
我在这里将位于经济上限和缓和发行之间的选项称为 “削减发行”。 此类别的限制有点模糊,但它试图捕获可能用于具有 MEV 销毁的以太坊的奖励曲线,但仍未追求经济上限。 图 15 显示了三个示例,粉色曲线接近类别(2),紫色奖励曲线接近类别(4)。 黑色显示当前的奖励曲线,灰色表示作为(2)一部分的有上限的发行曲线的限制,以供参考。
图 15. 三个大幅削减发行量的奖励曲线,但没有明确限制权益参与。
粉色和紫色曲线依赖于尽可能对当前协议进行最小调整的相同策略,正如之前介绍的那样。 粉色曲线的方程式为
y_i = \frac{cF}{\sqrt{D}+(D/k)^2}
其中 k=2^{19}。 紫色曲线的方程式为
y_i = \frac{cF}{\sqrt{D}(1+(D/k)^2)}
其中 k=38\times10^6。 图中的所有奖励曲线都具有 F=64。 在已经建立了 MEV 销毁之后,这些在整个范围内都具有正发行收益的奖励曲线背后的一个想法是向单人质押者保证,发行收益将始终保持为正。 当然,质押收益(发行 + MEV)应该直观地始终保持为正,因为除非内生收益为正,否则进行质押毫无意义。 但这里的保证与发行收益有关,这意味着在某些 MEV 仍然存在的情况下(由于例如部分 MEV 销毁或共识层预确认),单人质押者可能始终能够在更常规的基础上享受正收益(即使没有不时地被分配为提议者)。
紫色曲线减去 (D/k_2)^2,其中 k_2=9\times10^8。 效果是质押收益逐渐变为负数,但永远不会变为负无穷大。 这是一种更克制的使用负收益的方式。 实际上,效果会非常相似。 一些假设的好处是,均衡不会发生在收益在限制处急剧下降的点(受高 MEV 情景的影响),并且质押者将更好地保证不会遇到两位数的负收益(当然无论如何都不应该发生)。 一个缺点是没有可以限制权益数量的硬性保证。 图 16 显示了质押收益(包括每年 300k ETH 的执行层奖励),图 17 显示了发行收益(没有 MEV)。
图 16. 在三个削减发行量的奖励曲线下的质押收益。
图 17. 在三个削减发行量的奖励曲线下的发行收益。
4. 经济上限
经济上限由 Vitalik 提出,作为保证权益数量不会超过某些设定限制的一种方式。Caspar 和 Ansgar 最近提供了关于经济上限的更广泛的撰写,包括在(2)之后应用(4)的概念。 Vitalik 的奖励曲线可以概括为
y_i = \frac{cF}{\sqrt{D}} - \frac{cF_c}{\sqrt{l-D}},
这里将方程式调整为可以轻松直接纳入协议规范的格式。 第一项是当前的奖励曲线,第二项从中减去。 由于当限制 l=D 时,第二项将变为无穷大,因此质押收益将在该点变为负无穷大,从而限制权益数量。 Vitalik 使用了 l=2^{25}。 变量 F_c 塑造了达到上限之前的减少幅度,并在 Vitalik 的曲线中设置为 32(由他的方程式中的 0.5\times64 暗示)。 图 18-21 以红色显示了这条奖励曲线。
Vitalik 方程式的第一项可以根据需要替换为其他奖励曲线,以允许以太坊在 20M-40M ETH 左右的关键区域产生理想的发行量,其中均衡是最理想的。 使用前一小节中的紫色曲线得出方程式
y_i = \frac{cF}{\sqrt{D}(1+(D/k)^2)} - \frac{cF_c}{\sqrt{l-D}}.
图 18 显示了由此方程式产生的奖励曲线,上限设置为 l= 60M ETH(权益的 1/2;橙色),l= 80M ETH(权益的 2/3;黄色)和 l= 90M ETH(权益的 3/4;石灰)。 所有曲线都具有 k=2^{26} 和 F_c=2^4。
图 18. 在执行经济上限的奖励曲线下的发行量。 红色奖励曲线是 Vitalik 之前的提案,其他三个奖励曲线将存款规模分别限制在 60M ETH、80M ETH 和 90M ETH。
图 19 显示了质押收益(包括每年 300k ETH 的 MEV),图 20 显示了发行收益(没有 MEV)。
图 19. 在执行经济上限的奖励曲线下的,包含 300k ETH MEV 的质押收益。 红色奖励曲线是 Vitalik 之前的提案,其他三个奖励曲线将存款规模分别限制在 60M ETH、80M ETH 和 90M ETH。
图 20. 在执行经济上限的奖励曲线下的发行收益。 红色奖励曲线是 Vitalik 之前的提案,其他三个奖励曲线将存款规模分别限制在 60M ETH、80M ETH 和 90M ETH。
由于相对较高的可变性,在 MEV 下在低权益数量下设置上限是不可取的,正如之前的回答中所讨论的(1, 2)。 我认为,如果要追求以太坊经济上限,那么即使在 MEV 销毁之后,在 60M ETH 或更高水平设置上限的奖励曲线似乎更有希望。 在特别低的供应曲线下,这将允许权益数量有所扩大。 然而,设置上限可以提供最终的保证,并且从宏观角度来看,这可能非常有用。 在更高的权益参与度下,扩张路径因此应该可以论证地冒险进入负发行收益(这仍然会导致均衡状态下的正内生质押收益),并且该扩张路径最终可能会达到如此低的负区域,以至于只能通过经济上限才能达到。 简而言之,权益参与度非常大的负面影响比发行收益非常低的负面影响更糟糕。
所提出的方程式系统的一个有益特性是,上限不会涉及一些全新的方程式,而是可以被认为是,从 (2) 移动到 (4) 时的“一键开启”。 图 21 显示了一个示例,其中只需通过添加 Vitalik 的上限项(其中 l 等于 60M ETH、80M ETH 和 90M ETH),并将 F_c 设置为 10,即可更新先前展示的虚线绿色缓和发行曲线。
图 21. 开启经济上限。 通过添加上限项(将权益数量限制为 60M ETH、80M ETH 和 90M ETH,完整绿线)来更新以虚线绿线表示的缓和发行奖励曲线。 Vitalik 原始的经济上限奖励曲线以红色显示。
5. 时间–数量策略
正如之前一篇论文的 6.3 节 的最后一段所述,将时间维度添加到数量维度也值得考虑作为最终状态。 在时间–数量策略下,用户在较短时间范围内面临的奖励曲线可以具有适度的预定义形状,但允许整个曲线逐渐适应由均衡状态暗示的供应曲线的变化。 该机制的实施方式是,让定义该曲线的一个或两个变量,对偏离某个目标值的存款率做出响应时发生漂移。 这种漂移可以很容易地实施为每个 epoch 的小幅度变化,幅度的大小可能取决于或不取决于偏差的程度。
一个关键的认识是,奖励曲线变量应该缓慢变化,更大的影响发生在几年甚至几十年这个时间尺度上。 这样做的原因有几个,与先前答案中讨论的,以固定数量的权益为目标时所涉及的问题有关。 如果在发行量增加方面没有立即的响应,那么劝退攻击和卡特尔攻击可能会变得不那么有吸引力。 此外,如果短期奖励曲线更平坦,协议将产生更稳定的收益。 从沟通的角度来看,该机制始终提供清晰的轨迹,而尝试仅依赖于时间会使发行轨迹更难以解释。 最后,该机制提供了一种自然的方式,可以从一种发布策略过渡到另一种发布策略,而不会造成中断。 一个明显的缺点是增加了设计的复杂性。 正如本小节末尾所示,也可以通过不依赖于固定目标,而是依赖于基础目标奖励曲线,来更严格地保留预算编制的概念。
图 22 显示了在时间–数量策略下的年度发行量。 对于此示例,先前展示的具有缓和发行量的奖励曲线被用作潜在的起点,以虚线绿色显示。 30M ETH 的目标用深灰色垂直线标记,位于蓝色十字之间。 如果权益数量高于目标,类似于前一小节中描述的上限缓慢生效,逐渐移动奖励曲线,如浅绿色所示,从而降低收益。 在无限时间内,对于某些固定的供应曲线,均衡将位于灰色垂直线上,或者位于边缘的黑色曲线上,黑色曲线描述了对奖励曲线的最大和最小允许设置。 在本示例中,这对应于当前的奖励曲线为最大值,80M ETH 的上限为最小值(权益的 2/3)。 应该注意的是,时间–数量策略不需要最小奖励曲线实施经济上限。 在某种程度上,在无论如何都没有明确保证某种上限的情况下,此策略甚至更合适。
图 22. 具有上限的时间——数量策略下的发行量。 发行量水平将沿着绿色奖励曲线的轨迹对存款权益的变化做出反应。 然而,在无限时间尺度上,如果供应曲线保持固定,则奖励曲线会进行调整,从而沿着黑色路径实施均衡。
对于发行收益,图 23 显示了相同的策略。 在无限时间尺度上,用户将面临构成上部黑色曲线的奖励曲线,然后是灰色垂直线,最后是下部黑色曲线。 但是,在几个月或可能一两年的时间尺度上,用户将面临沿着绿色细线之一的奖励曲线,该曲线会立即对权益数量的直接变化做出反应。 在几年时间尺度上,用户将面临介于两者之间的情况 —— 当前轨迹的平滑版本,朝着奖励曲线的黑色和灰色部分漂移。
图 23. 具有上限的时间数量策略下的发行收益。 有关详细说明,请参见图 22 的图说文字。
时间–数量策略背后的一个想法是,随着与质押相关的相对成本的降低,供应曲线可能会缓慢下降,并且如果不使奖励曲线接近垂直,我们则无法随时间推移实施某些特定的权益数量。 正如先前所讨论的,垂直奖励曲线似乎不可取的原因之一是它带来了较高的 “p_i 弹性”。
即使某些特定的权益数量是最佳的,从长远来看,也可能需要考虑预算因素。 毕竟,首先规定不为安全性支付过高的费用,是使用奖励曲线的好处。 图 24 显示了在具有上限的平滑时间数量策略下的发行量。 它试图实现两全其美:从长远来看,更严格的范围仍然包含一些预算编制的概念; 对于短期而言,更加平坦的奖励曲线,调节了收益/发行量的波动,并基于供应曲线最近的稳定状态进行的预算编制。 黑色曲线是无限时间尺度下的目标奖励曲线。 从短期来看,协议仍将根据绿色奖励曲线运行,从而根据权益数量的变化来调整收益。
图 24. 具有上限的平滑时间数量策略下的发行量。 发行量水平将沿着绿色奖励曲线的轨迹对存款权益的变化做出反应。 然而,在无限时间尺度上,如果供应曲线保持固定,则奖励曲线会进行调整,从而沿着黑色路径实施均衡。
对于发行收益,图 25 显示了相同的策略。
图 25. 具有上限的平滑时间数量策略下的发行量。 有关详细说明,请参见图 24 的图说文字。
时间–数量策略尚未经过研究和辩论,增加的复杂性是否值得将在将来的讨论中解决。
为什么不阻止新的质押者加入?
控制验证器的人员随后将持有“质押许可证”,类似于出租车许可证或租金管制下的租赁公寓。 这将创建副市场,并且单人质押者不一定非常适合驾驭这些情况。 这种准许可系统通常会使“内部”的质押者能够对链行使不正当的控制权,并可能导致寻租行为。
质押者可以从减少的发行量中获利吗?以及真实/比例产量的重要性及其影响是什么?
概述
质押者持有基础的 ETH,如果发行量减少能够改善以太坊,从而使原生资产更有价值,则可以获利。 此外,就像其他人一样,质押者也会因新发行的代币而被稀释。 因此,如果高发行量迫使许多人进行质押,那么那些即使在较低发行量下也会进行质押的人(竞争收益的质押者更少)可能会从较低的发行量中受益。 剩余质押者所获得的 ETH 比例是否会因发行量减少而增加(如下定义的正 y_p)绝不是确定的,但是任何潜在的损失将比发行收益变化所暗示的幅度小得多。 条件在图 28 的等比例地图中进行了说明。
福利增益 —— 作为 ETH 持有者的质押者
当讨论发行政策对 Staker 的影响时,首先要认识到他们拥有底层的 ETH。一个设计良好的去中心化区块链的原生资产比设计糟糕的更有价值。在下面的小节中,将分析比例收益/实际收益,考虑到发行和销毁。但最终,以太坊为世界经济提供动力的能力将对 ETH 代币持有者(包括 Staker)产生最大的影响。真正的“实际收益”包含底层 ETH 的价值变化(包括任何 Staking 收益)相对于相关的消费者价格指数。在一个经济系统中拥有健全的原生货币确实非常有用。而且,最好的健全货币不会让其用户承担研究各种 SSP 的可靠性、追踪 Staking 收入并缴纳税款,或者面临在 Slashing 事件或其他故障中被清除的风险。
比例收益
回顾图 26,它是图 1的更新版本。再次,回顾了在均衡状态下发行量变化的影响,福利的改善用深蓝色区域表示。深灰色区域的高度代表了 Staker 的收益 y 的损失,用红色箭头表示。但是,当发行量减少时,每个人也会以降低发行率 i 的形式获得深蓝色和深灰色区域的组合比例份额。
该图通过获取深蓝色区域和深灰色区域,并创建一个横跨整个流通供应量(1.2 亿 ETH)的矩形,来说明发行量变化对 ETH 持有者的影响。所有代币持有者都根据该区域的高度获得收益,如橙色箭头所示。如果该高度超过深灰色区域的高度,则 Staker 将从发行量减少中获得更高比例的流通供应量,否则不会。
图 26. 假设的未来供应曲线下 Staking 的隐含成本(蓝色)和盈余(灰色)。发行政策的变化将均衡状态从黑色方块转移到绿色圆圈。只要协议保持安全和去中心化,成本降低(深蓝色)就会导致总体福利的改善,而盈余的减少(深灰色)只是将一些效用从 Staker 转移到所有人。剩余的 Staker 会损失收益(红色箭头)。然而,他们会从通货膨胀率的降低中获益(橙色箭头),这由横跨整个 1.2 亿 ETH 供应量的深蓝色和灰色区域的组合表示。
发行率的形成方式为 i=y_id,其中 y_i 是发行收益,d 是 Staking 的流通供应量的比例。实际上,正是 d 和 y_i 的变化决定了图 26 中橙色箭头的高度(i 的变化)。发行率会根据 s=i-b 影响流通供应量的通货膨胀率。本质上,s 捕获了一年中 ETH 数量变化的百分比。这意味着如果发行率很高,s 就会上升。相反,如果通过 EIP-1559 销毁大量 ETH,s 就会下降;由于 The Merge 的示例,本文将使用近似销毁率 b=0.008。可以使用我在关于最低可行发行量的帖子中提出的公式来计算对代币持有者的影响:
y_p = \frac{1+y}{1+s}-1.
比例收益 y_p,也称为实际收益,可以为 Staker 和非 Staker 计算,后一种情况 y=0。它可以被解释为适用于以太坊的费雪方程式。一个简单的近似值,适用于较低的收益率,是 y_p=y-s。
说明福利和比例收益的变化
图 27 再次说明了在减少 ETH 持有者发行量的情况下会发生什么,使用与图 26 相同的供需曲线。有三个类别:剩余的 stakers、供应曲线上绿色圆圈和黑色方块之间的 de-stakers,以及从一开始就是 non-stakers 的人。这个想法是比较所有代币持有者在两种不同均衡状态下的 y_p,因为它从 y^b_p(黑色方块)变为 y^a_p(绿色圆圈)。如果 y^a_p 较高,则代币持有者受益,否则会遭受损失。比较给出了基数效用的变化,如
u’=\frac{1+y^a_p}{1+y^b_p}-1.
但是,需要添加一个:对于那些在计算 y^a_p 时停止 Staking 的人,使用保留收益作为 y。低于该收益率,他们无论如何都不会 Staking,因此随着收益率进一步降低,他们不会遭受额外的效用损失。如下面的窗格所示,根据此定义,De-Staker 将在新均衡中获得更高的效用,而非 Staker 显然会更好。
图 27. 利用两种假设均衡之间的 y 和 s 的变化来隔离所有代币持有者的基数效用 u' 的变化。Staker 会受到收益 y 降低的影响,但通货膨胀率 s 的降低类似,因此他们不受影响(y_p 保持不变)。一旦 y 降至其保留收益以下,De-Staker 不会遭受进一步的效用损失。他们与非 Staker 一起从 s 的降低中受益。
底部窗格中的橙色箭头再次说明了 s 的降低如何增加每个人的效用——这是因为取消了前一张图中的深灰色和深蓝色区域。红色箭头说明了收益的降低如何减少 Staker 的效用,这与图 26 中深灰色区域的高度相对应。对于 De-Staker,即使他们放弃了所有收益,红色箭头也会变得非常短,因为深灰色区域会缩小。这是因为他们的成本也降至 0。
因此,u' 的高度捕获了 Staker 和非 Staker 的 y_p 的变化,橙色区域的大小捕获了福利的增加,最终源于以太坊用户成本的降低(请注意,橙色区域进一步延伸至 1.2 亿 ETH)。虽然 Staker 在保留的流通供应量比例方面可能不受发行量减少的影响,但他们仍然可以获得收益,因为 ETH 资产的效用已经增加,这与橙色区域的大小一致。我在关于最低可行发行量的原始帖子中引入此图的目的是将这些见解(福利收益 + 比例收益)封装在一个图中。
等比例图
显然,在确定 Staker 是否从减少发行中获益时,供应曲线的形状将具有影响力。如果收益 y 上升,但没有新的 Staker 进入,则在陡峭的供应曲线下,Staker 从增加发行中获益。如果收益的轻微提升导致大量新 Staker 进入,从而导致流通供应通货膨胀 s,则在平坦的供应曲线下,Staker 不会获益。在经济学中,通常使用图表通过绘制条件保持不变的线来表示权衡取舍,类似于地形图上指示相等海拔高度的等高线。图 28 显示了这样的图,其中“等比例线”指示 y_p 保持不变的位置。每条线都根据以下公式绘制:
y = \frac{y_p-(1+y_p)(v+b)}{1-d-y_pd},\quad \quad y_p<\frac{1-d}{d}.
这是通过重新计算 y_p 的公式形成的。这里的变量 v 表示“MEV 率”,即 MEV 占流通供应量的比例。该公式暗示了可以在任何均衡状态下强加于供应曲线的基本盈利条件(例如,通过弹性推导和分析)。
图 28. 一个等比例图,说明了 Staker 从发行政策变更中获得更高比例的流通供应的条件。如果相应的灰色等比例线的斜率比均衡状态下供应曲线的斜率更陡峭,则 Staker 从减少发行中获益。即使 Staking 收益更高,红色区域在该图上的海拔高度也低于橙色区域,因此对于 Staker 来说是一个更糟糕的均衡状态。
回顾紫色虚线等比例线。Staker 在该线上的任何位置都能获得 1.7% 的实际 Staking 收益,尽管 Staking 收益和 Staking 参与度会有所不同。红色区域位于该线下方,因此最终到达那里对 Staker 来说比最终到达该线上方的橙色区域更糟糕,即使整个红色区域的 Staking 收益都高于橙色区域。当几乎每个人都 Stake 时,如果 Staker 要从 Staking 收益的增加中获益,则供应曲线必须几乎是垂直的,因为供应通货膨胀率几乎会增加相同的幅度。橙色箭头指向等比例图上更高的海拔高度,Staker 的理想均衡状态位于左上角。但不幸的是,对于 Staker 来说,均衡状态必须位于供应曲线上。现在看看紫色完整等比例线。
来自之前图 26-27 的蓝色假设供应曲线沿着这条线与当前的奖励曲线(黑色)和具有缓和发行量的奖励曲线(绿色)相交——因此均衡状态(黑色方块和绿色圆圈)处于相同的“海拔高度”。这解释了为什么 Staker 在之前的讨论中没有受到影响。供应曲线的最高海拔高度用蓝色星形标记,位于两个均衡状态之间。在这一点上,供应曲线与相应的等比例线相切。Caspar 和 Ansgar 的图以及绿色奖励曲线的 Mike 的图对于显示其海拔高度 (y_p) 如何在 Staking 参与度中变化(不包括 MEV 或销毁)很有用。这类似于从地图上跨 Staking 参与度对其值进行采样。
供应曲线未来如何发展?利用你的直觉来概述它的形状,并检查你的假想供应曲线在地图上达到最高海拔高度的位置(如星形标记所示)。这就是奖励曲线应该与供应曲线相交的位置,以便 Staker 获得最高比例的流通供应量。但是,也要记住之前讨论中的教训:Staker 还可以通过持有设计良好的加密货币的原生代币来获得收益,该代币保持安全并对其用户施加较低的总成本。
一些用户认为更多的收益更有趣,并且喜欢收集他们的 ETH 收益。为什么不倾向于这样做呢?
此答案将扩展之前的答案(1、2),鼓励读者首先回顾它们,以了解过度的发行以及稀释如何影响代币持有者。
有限理性的概念有助于解释为什么一些用户可能更喜欢 y_p 较低的场景,其中收益提高,但供应通货膨胀率(用户更难追踪)甚至更高。行为经济学可以通过这种方式来解释为什么一些经济主体不理性地行事,可能是因为缺乏教育或没有时间来思考一个话题。但是,以太坊不应利用人们对收益的有限理解,并保持高收益来欺骗用户,让他们认为自己获得了收益,而实际上他们并没有。相反,重要的是教育人们有关这些事项,以便不会为了某些假设的短期收益而降低用户效用,而这种收益不太可能实现。更多的收益并不更有趣。一个经过优化设计的以太坊更有趣。
- 最大可行安全性:以太坊发行的新框架
- 规模不经济:反相关惩罚 (EIP-7716)
- 关于发行政策的实用结局
- Orbit/Vorbit SSF 中的合并激励
- 彩虹角色与激励:ABPS + FOCILR + AS
- 还有 2 个
- 原文链接: ethresear.ch/t/faq-ether...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 深入探究 ENSv2 架构 46 浏览
- 什么是DeFi?去中心化金融指南 - CoW DAO 48 浏览
- L1 价值捕获的压缩 24 浏览
- 以太坊怎么了? 34 浏览
- DeFi和加密货币之间有区别吗?——CoW DAO 41 浏览
- 什么是DeFi聚合器?——CoW DAO 42 浏览
- 顶级DeFi交易所:理解去中心化交易基础设施 - CoW DAO 178 浏览
- 以太坊 2026年协议级更新确定 3 大方向 272 浏览
- 寻找底线:为什么我们为 Layer 2 构建了紧急提款出口( Exit Hatch) 196 浏览
- Solana的区块构建之战 240 浏览
- 如何去中心化构建区块? 309 浏览
- Builder Codes & ERC-8021:修复链上归属问题 332 浏览

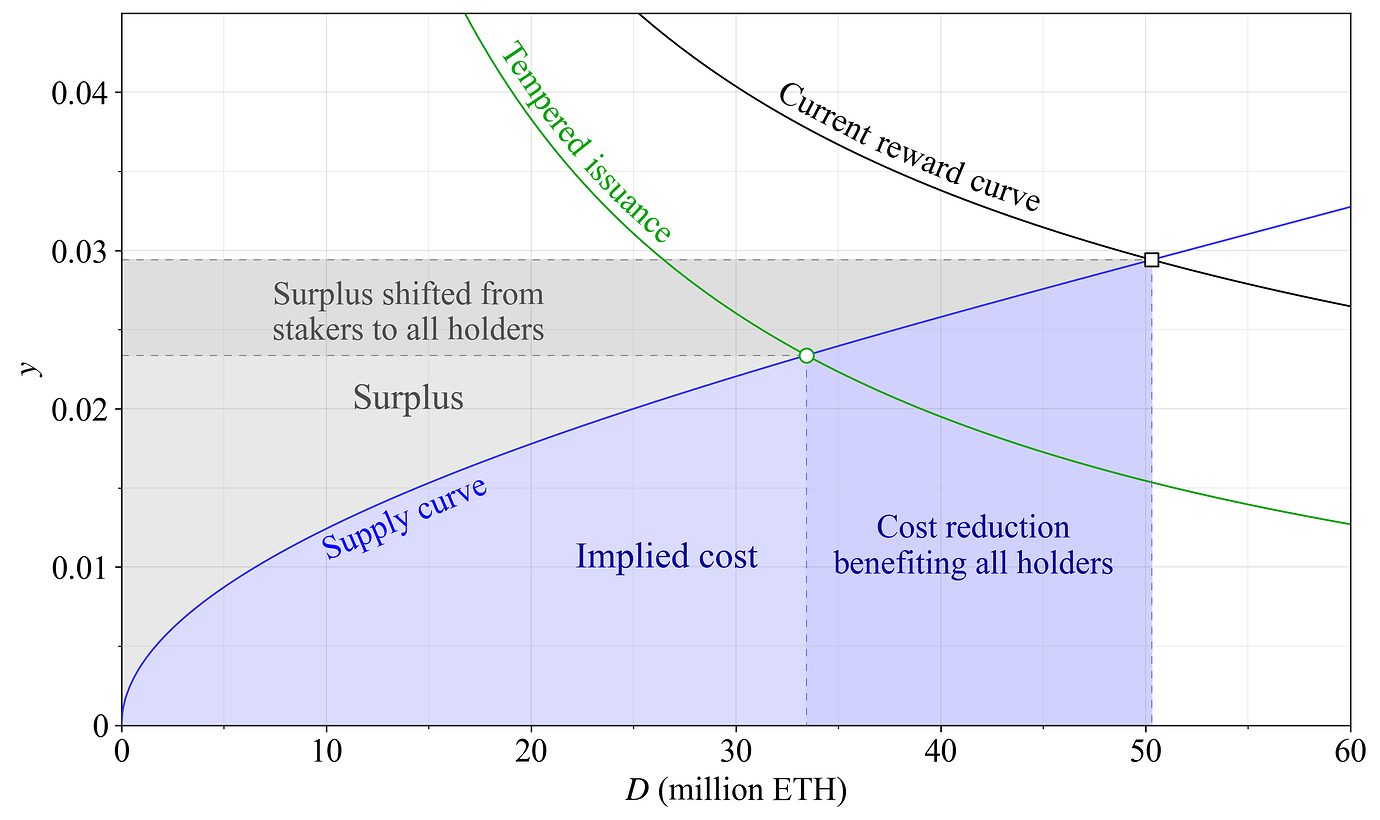 \
图 13133×1864 380 KB
\
图 13133×1864 380 KB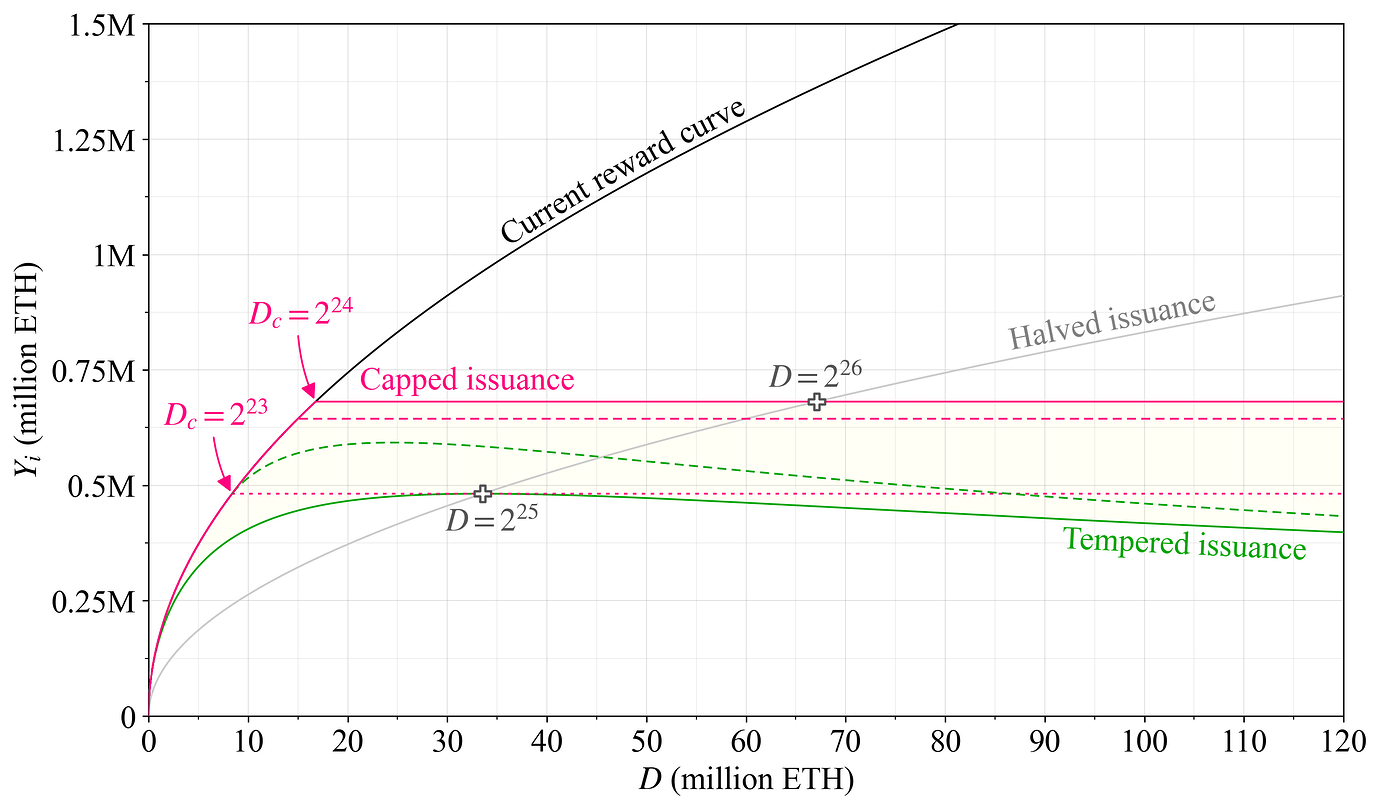 \
图 22685×1575 287 KB
\
图 22685×1575 287 KB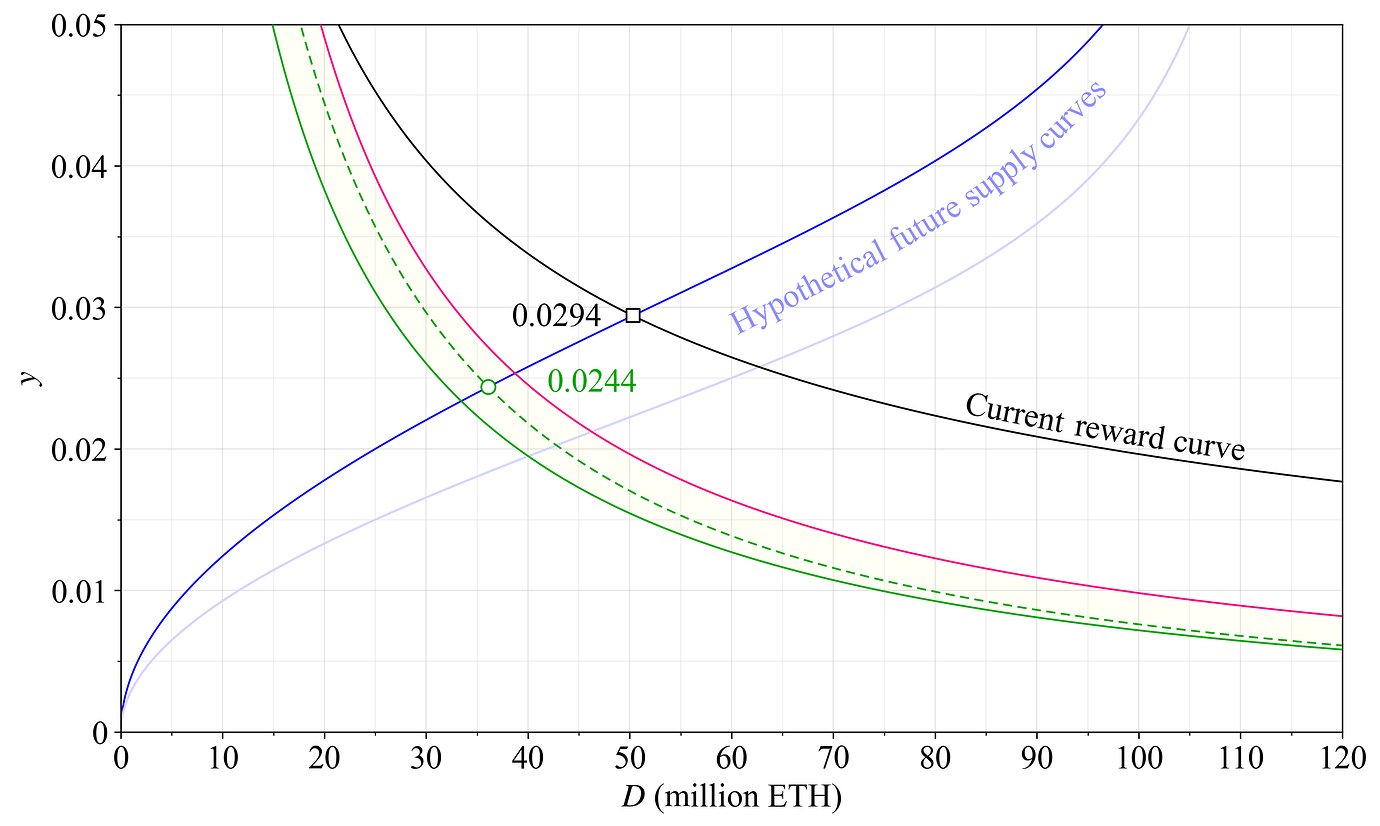 \
图 33152×1890 416 KB
\
图 33152×1890 416 KB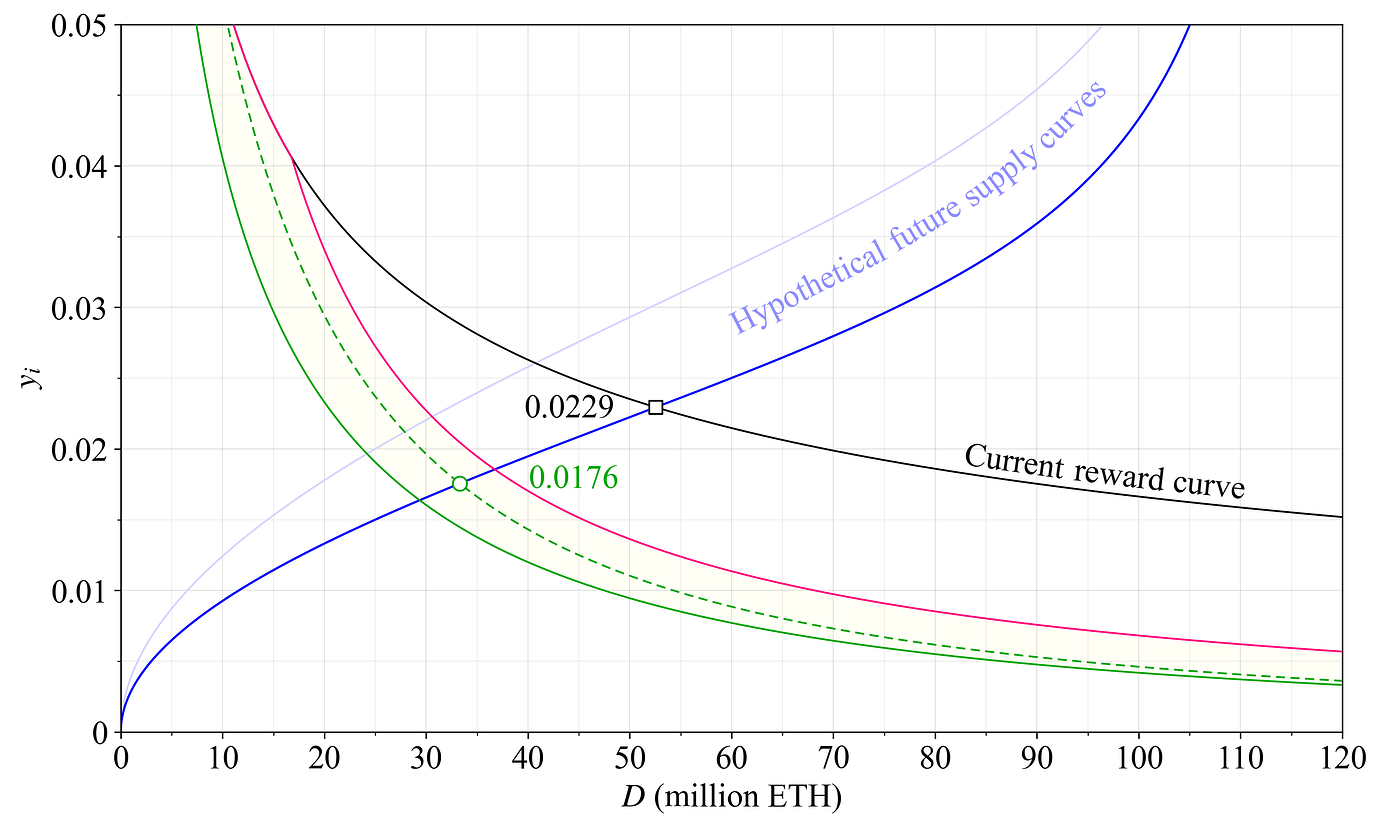 \
图 43152×1890 415 KB
\
图 43152×1890 415 KB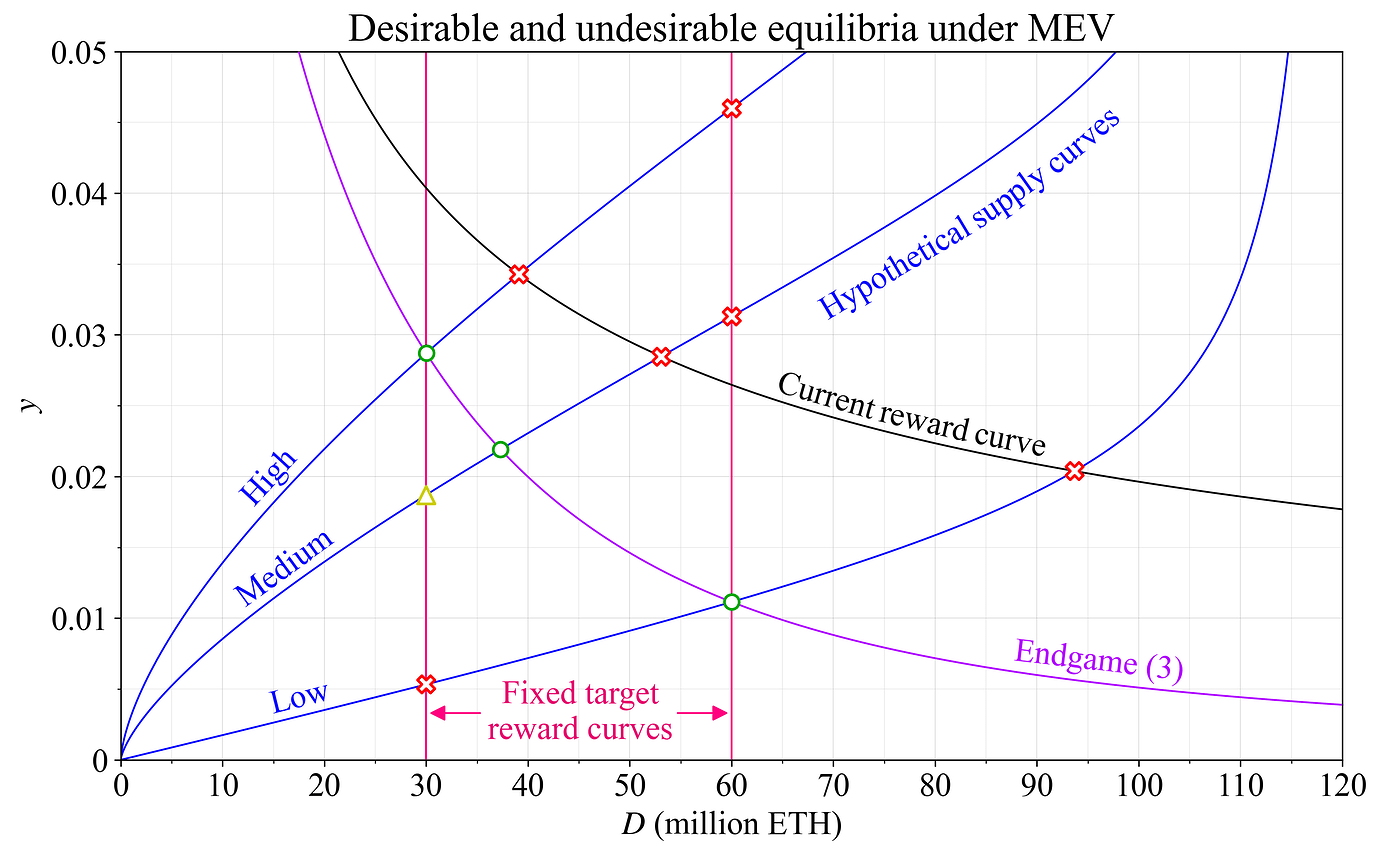 \
图 53152×1952 470 KB
\
图 53152×1952 470 KB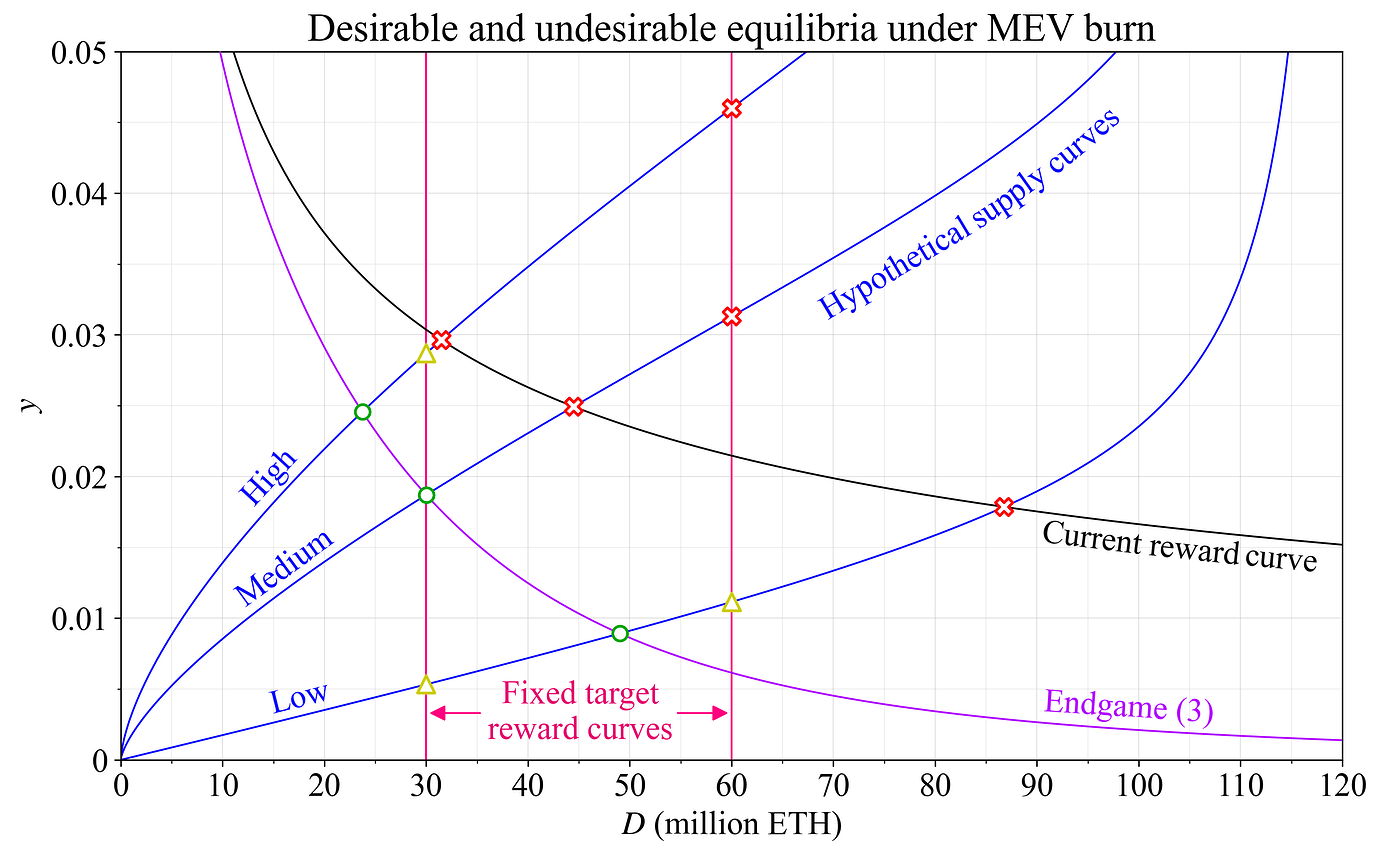 \
Figure 63152×1952 469 KB
\
Figure 63152×1952 469 KB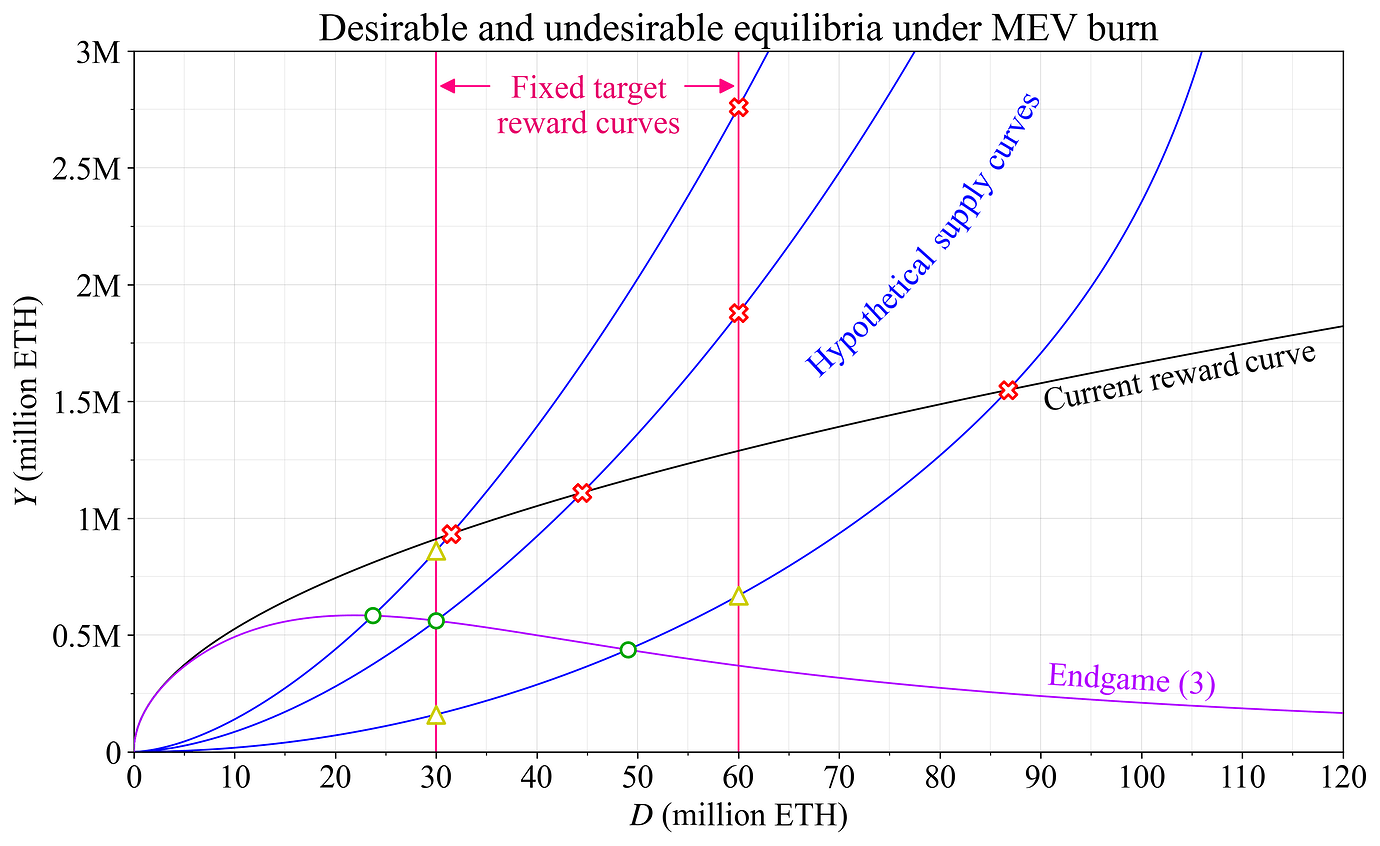 \
Figure 73184×1952 422 KB
\
Figure 73184×1952 422 KB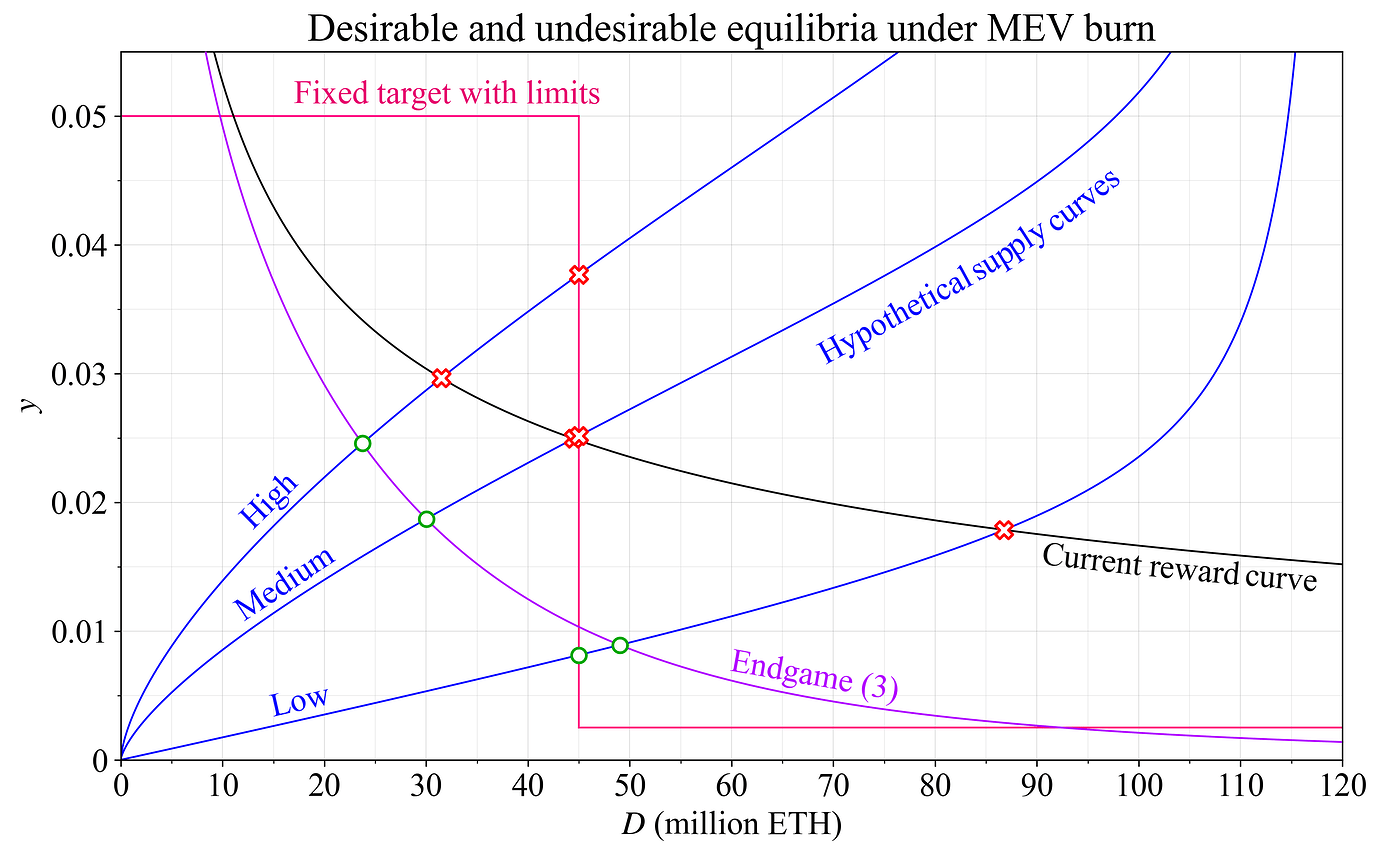 \
Figure 83152×1952 466 KB
\
Figure 83152×1952 466 KB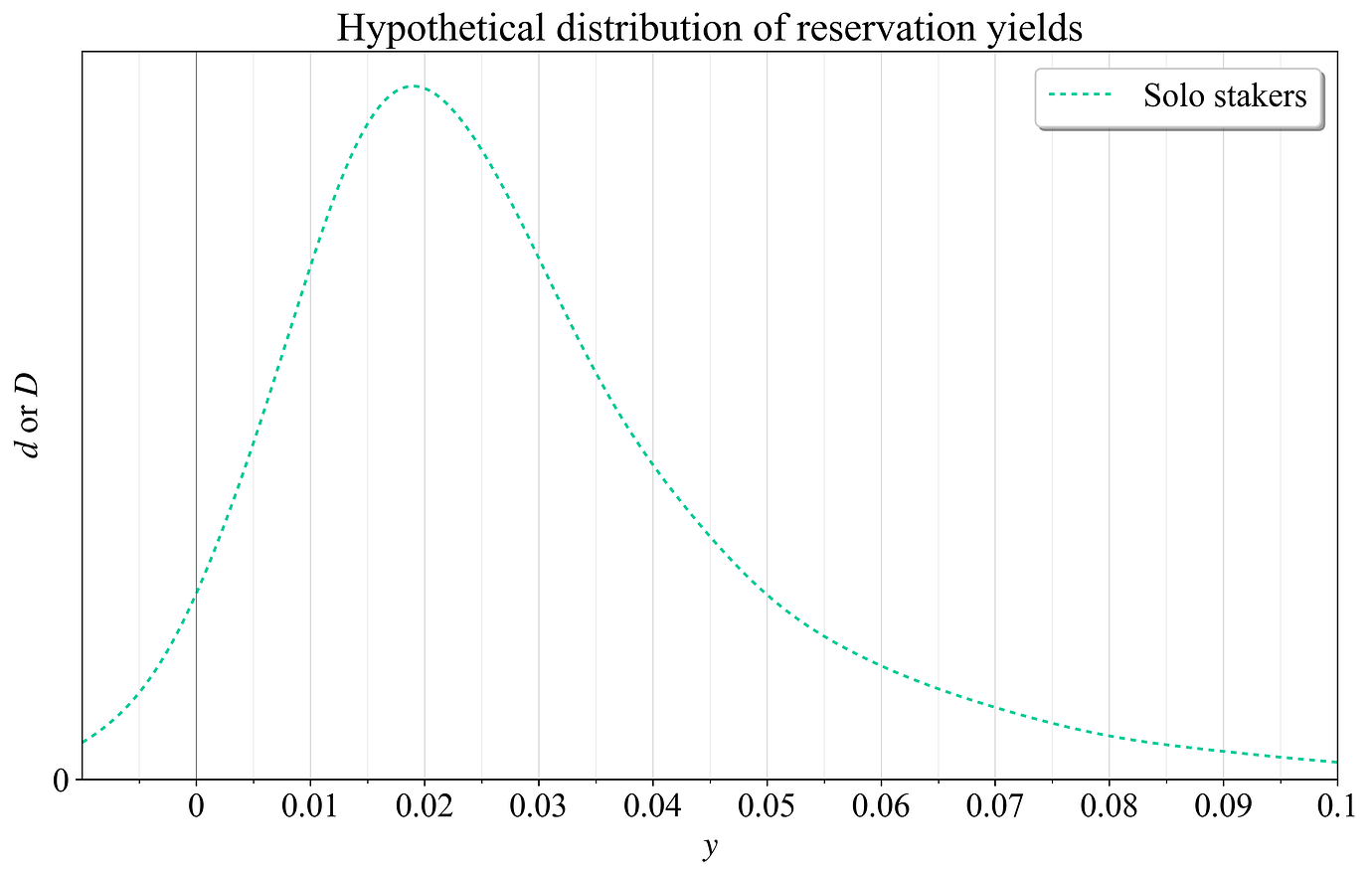 \
Figure 93557×2273 190 KB
\
Figure 93557×2273 190 KB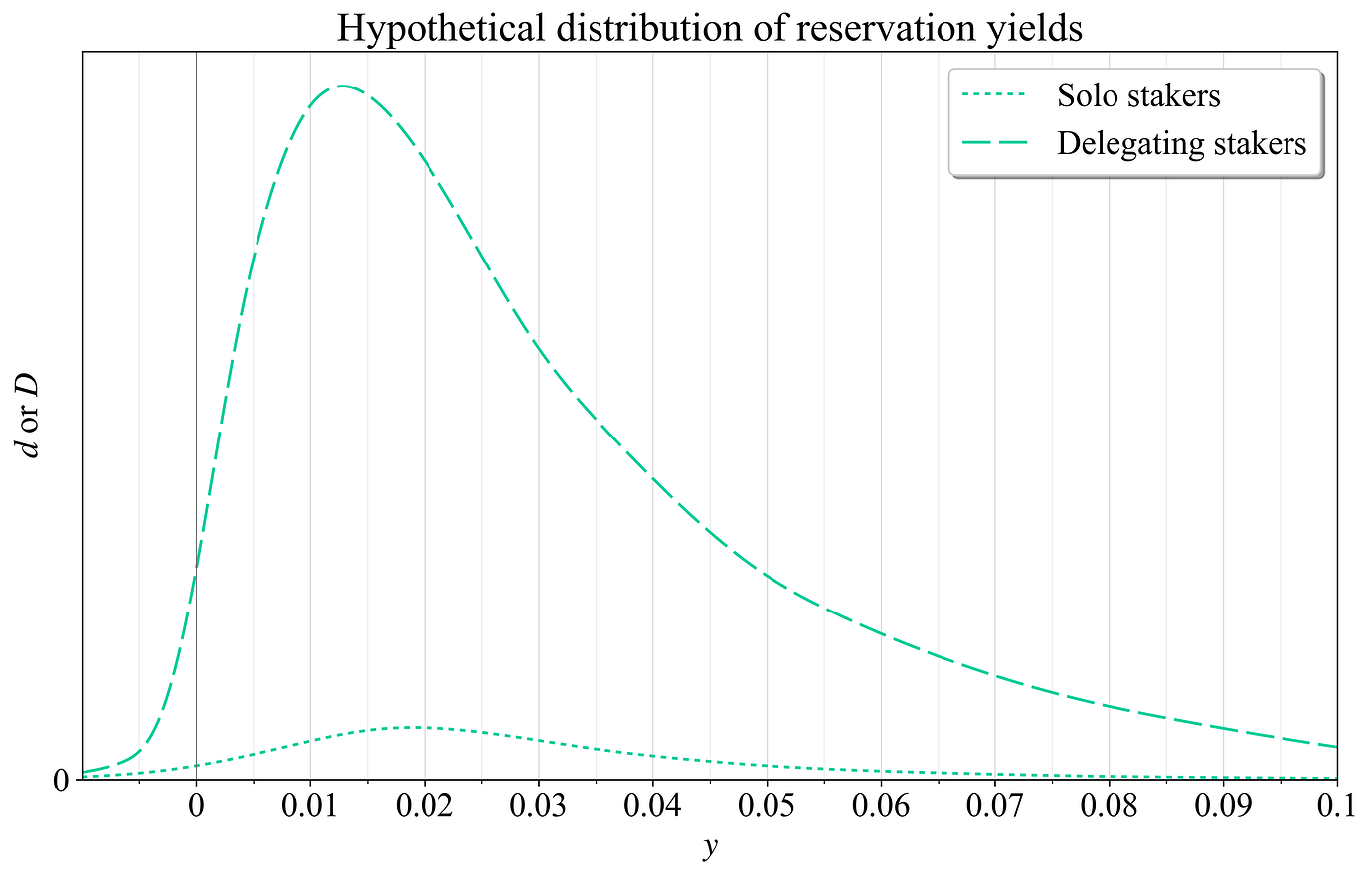 \
Figure 103557×2273 236 KB
\
Figure 103557×2273 236 KB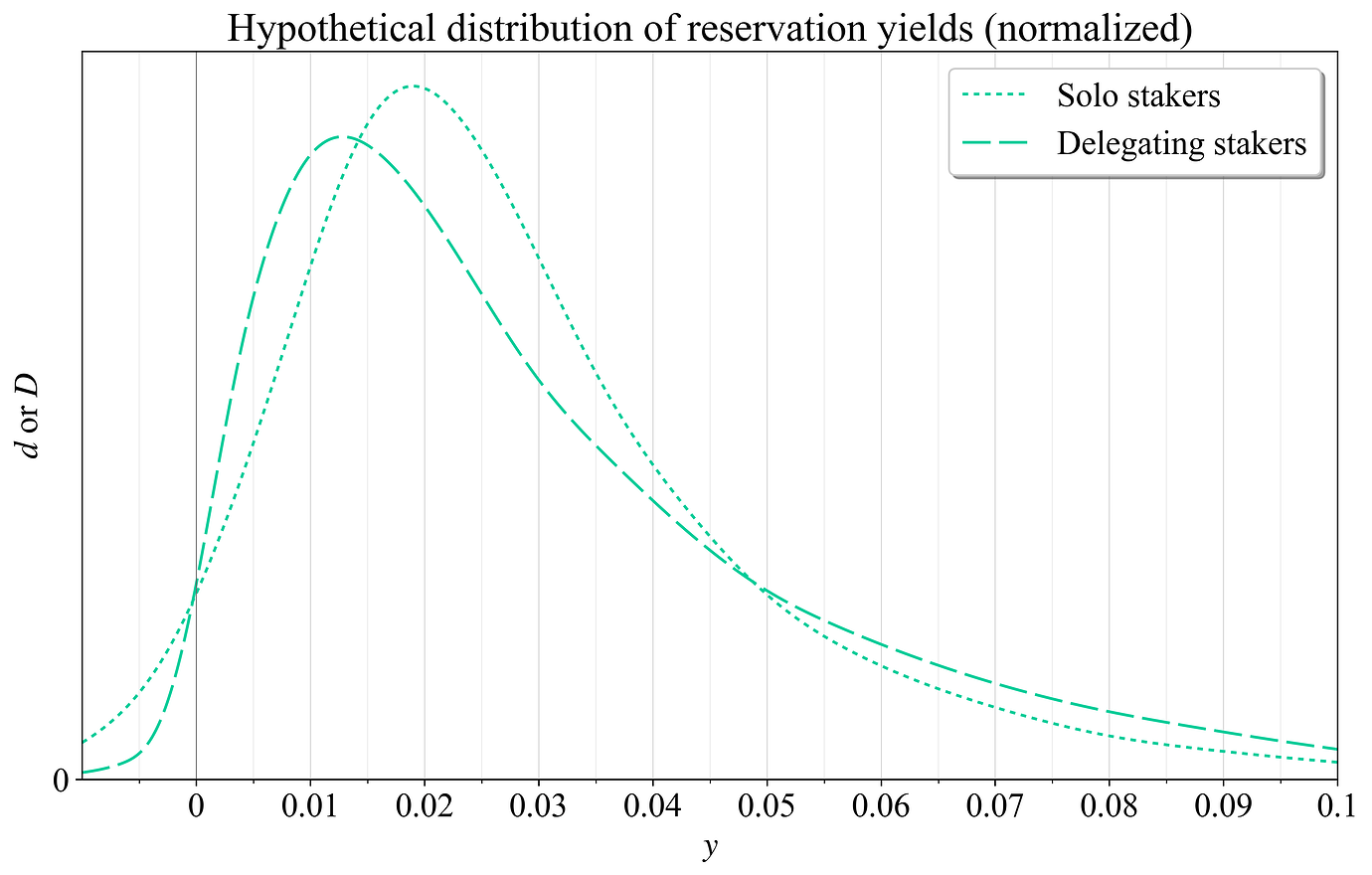 \
Figure 113557×2273 286 KB
\
Figure 113557×2273 286 KB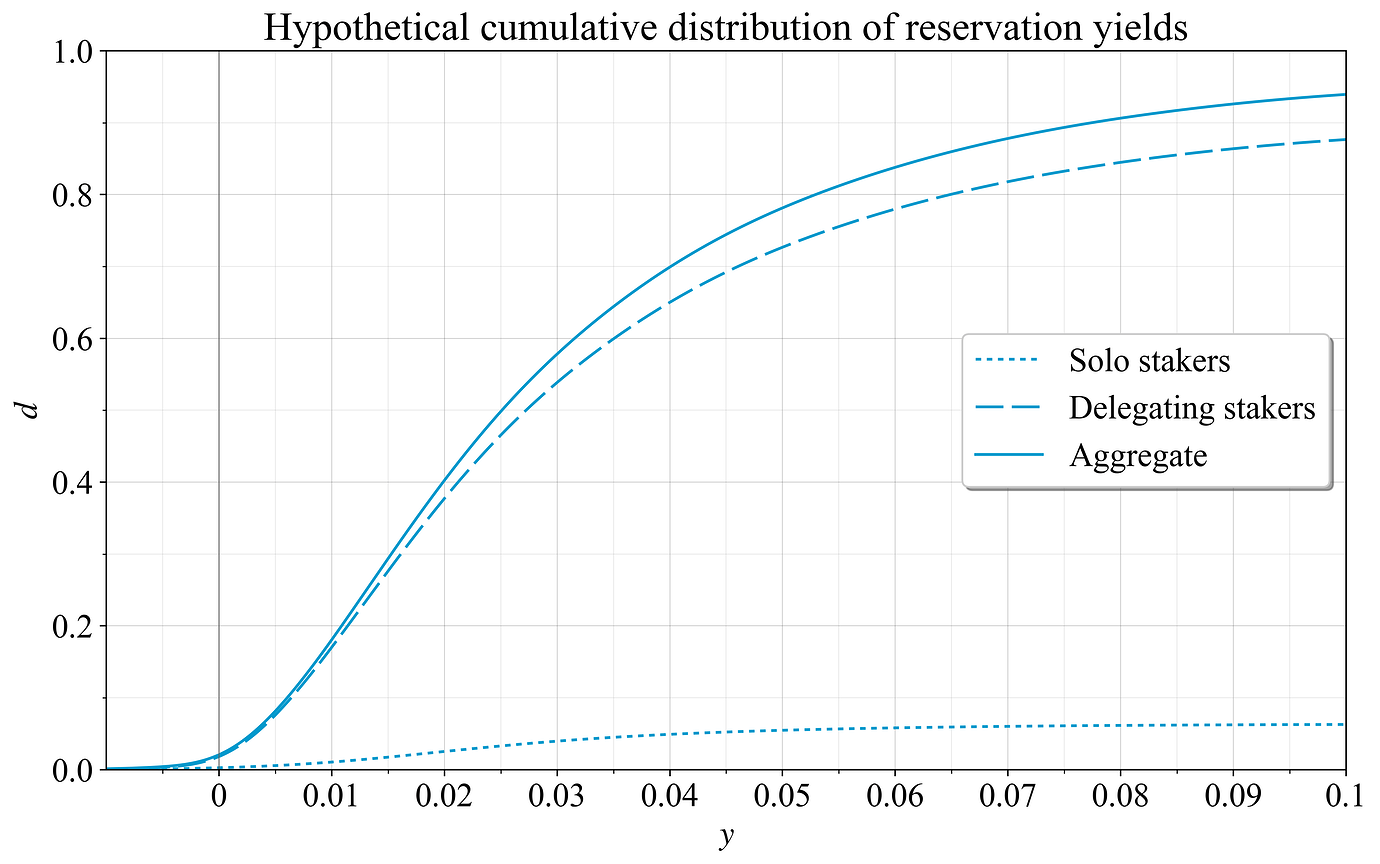 \
Figure 123623×2273 292 KB
\
Figure 123623×2273 292 KB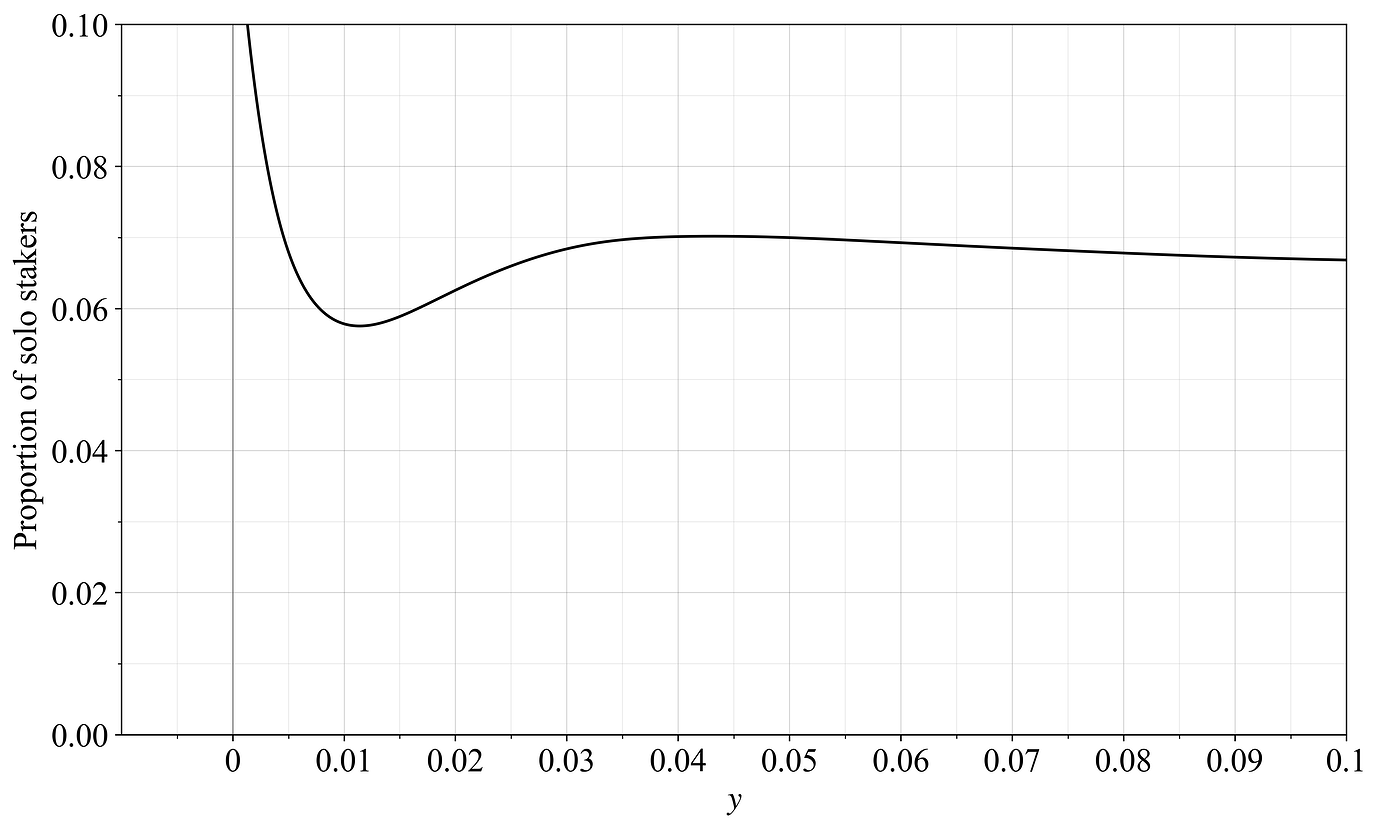 \
Figure 133667×2202 160 KB
\
Figure 133667×2202 160 KB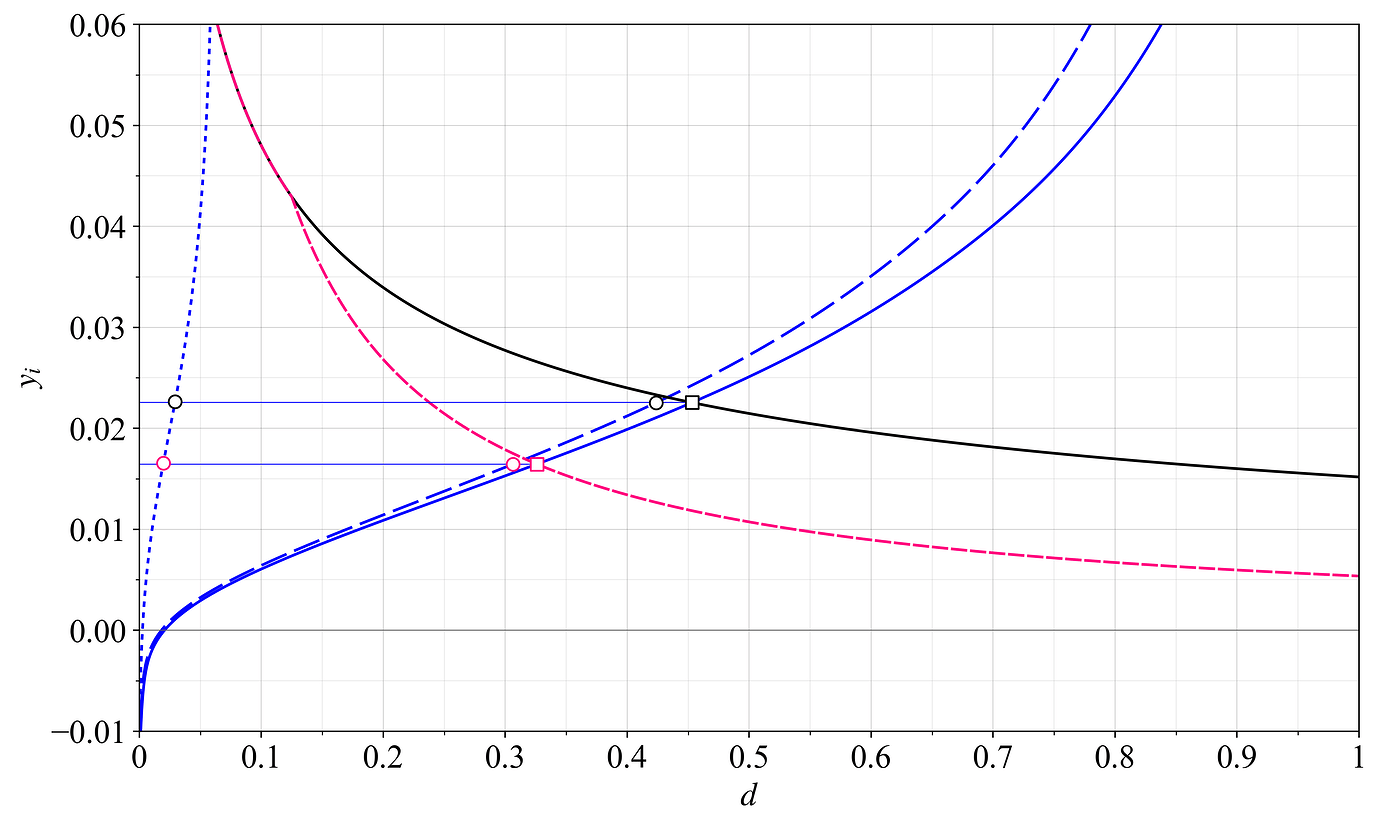 \
Figure 143683×2202 281 KB
\
Figure 143683×2202 281 KB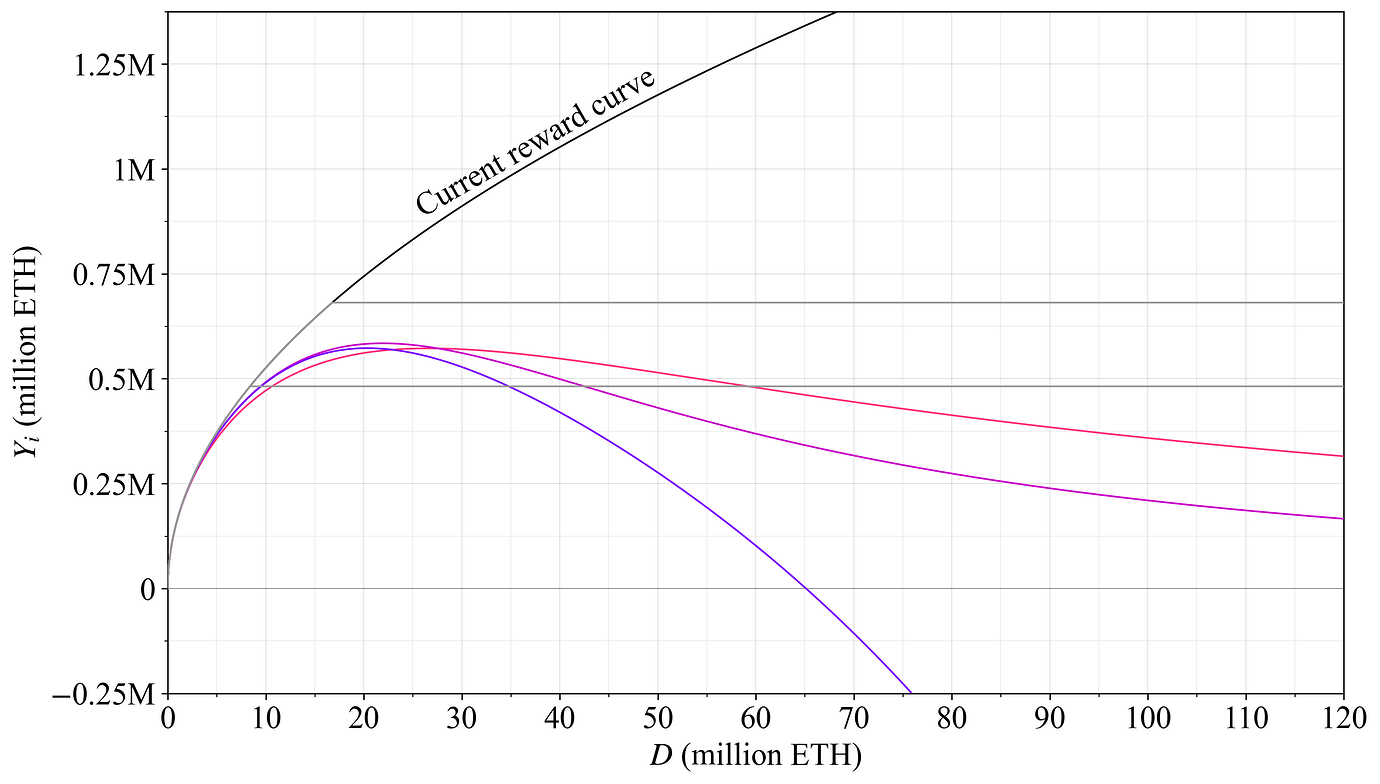 \
图 153274×1864 273 KB
\
图 153274×1864 273 KB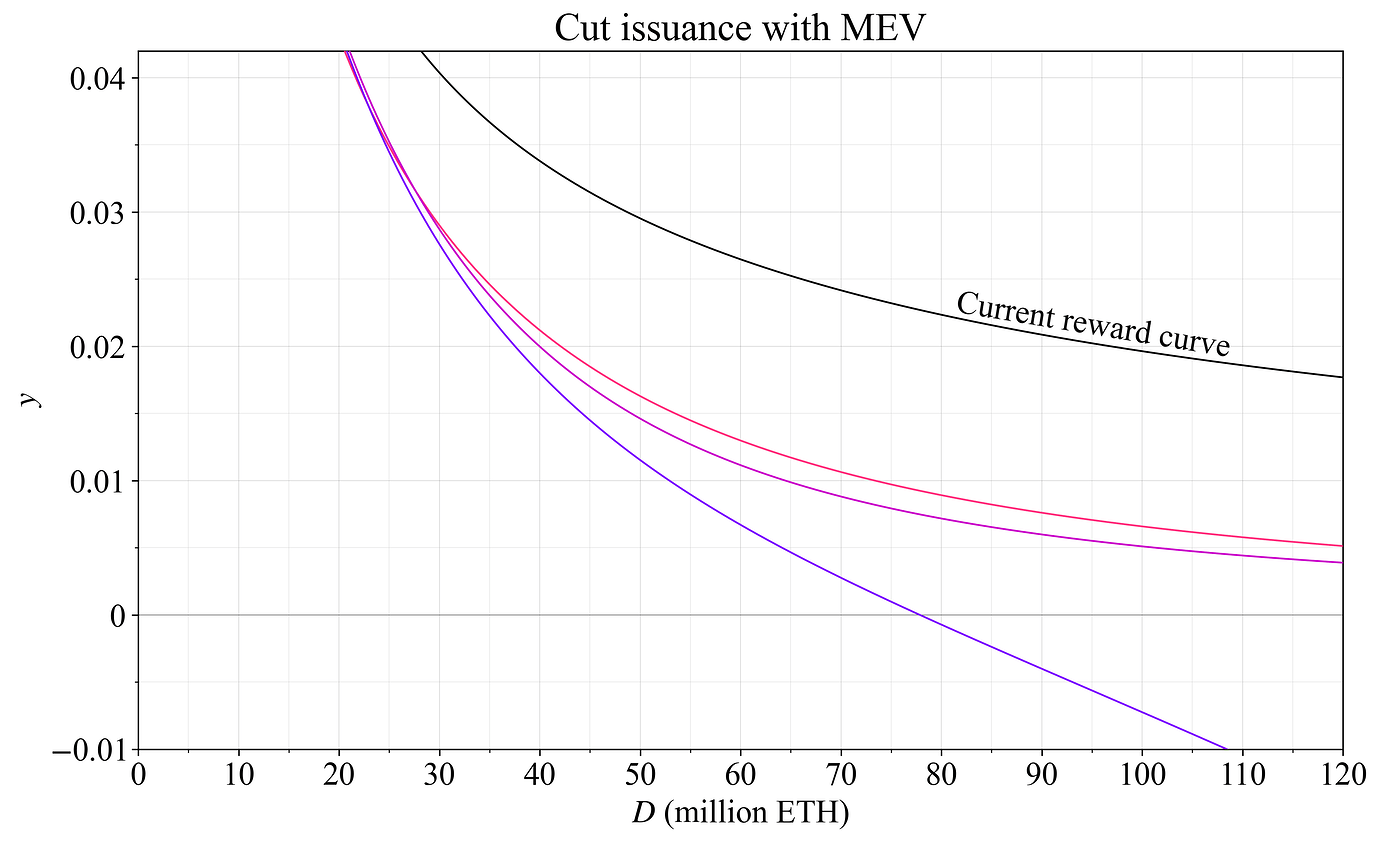 \
图 163196×1952 289 KB
\
图 163196×1952 289 KB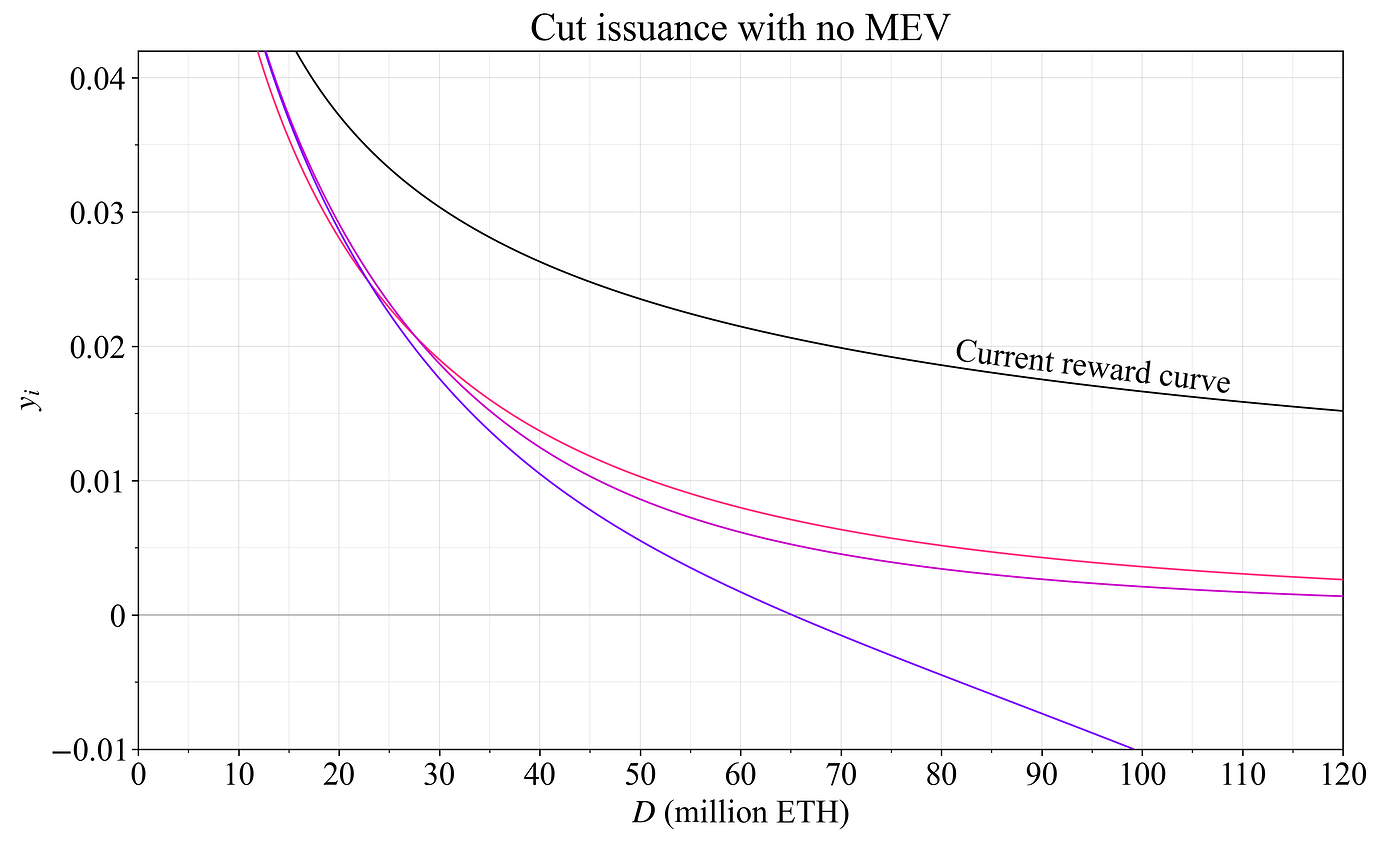 \
图 173196×1952 291 KB
\
图 173196×1952 291 KB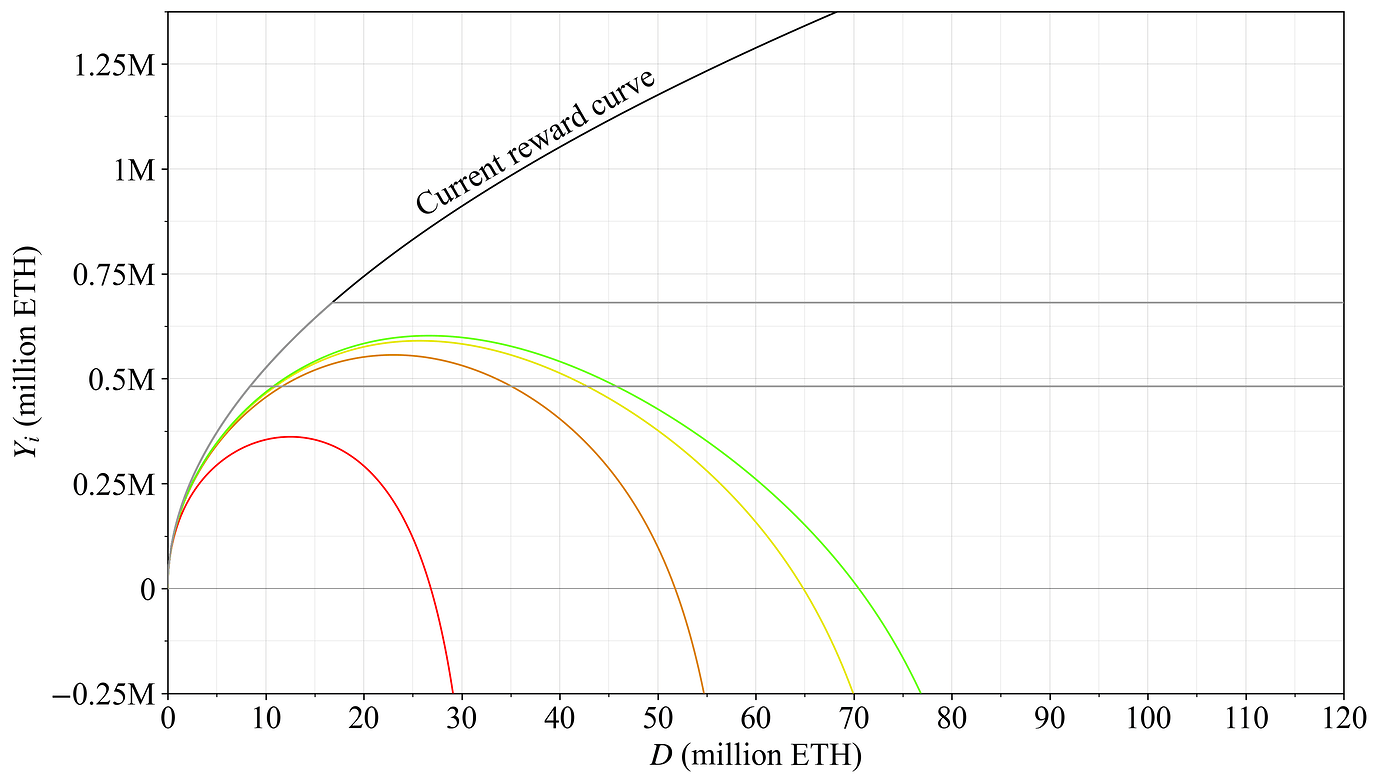 \
图 183274×1864 290 KB
\
图 183274×1864 290 KB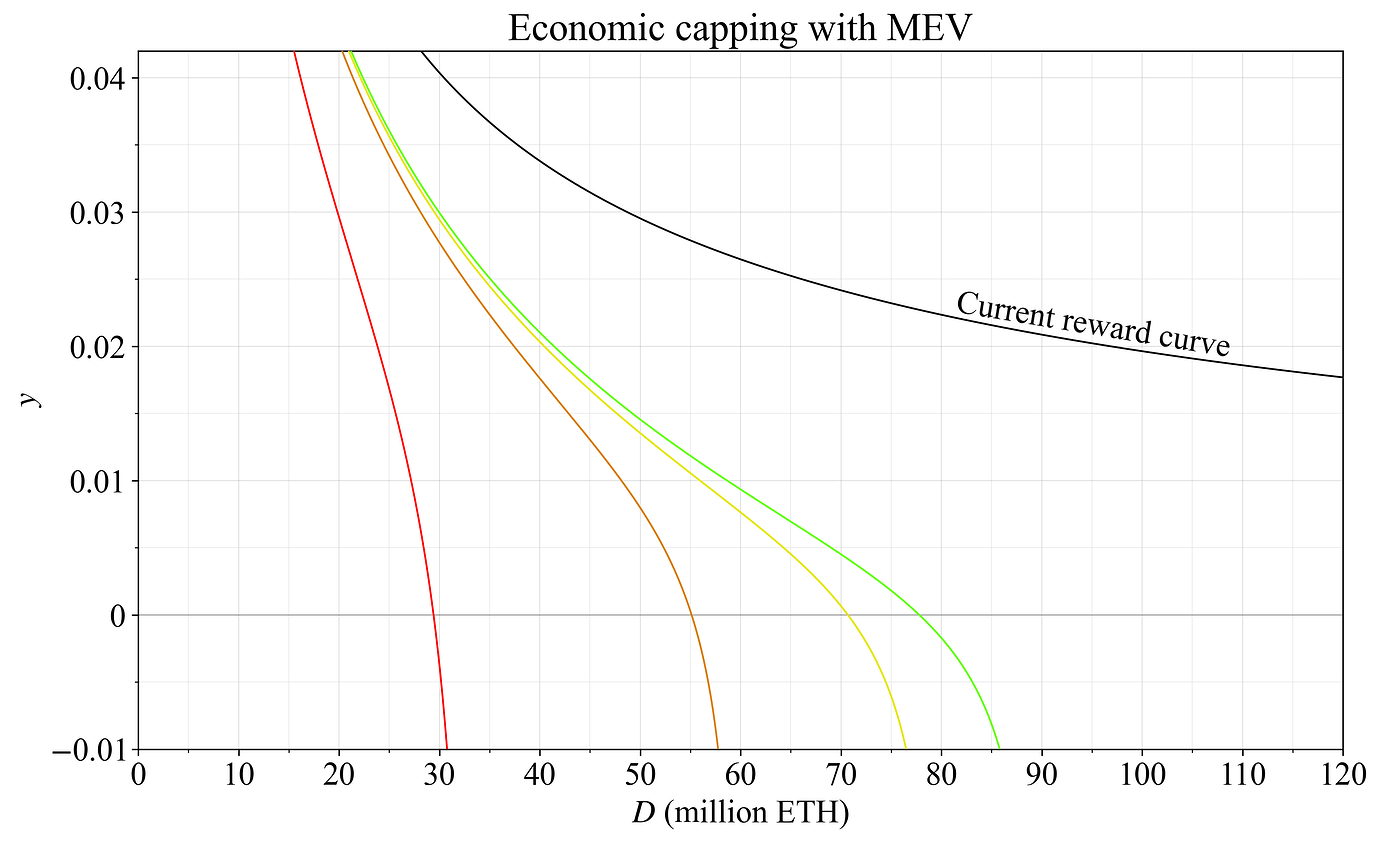 \
图 193196×1952 305 KB
\
图 193196×1952 305 KB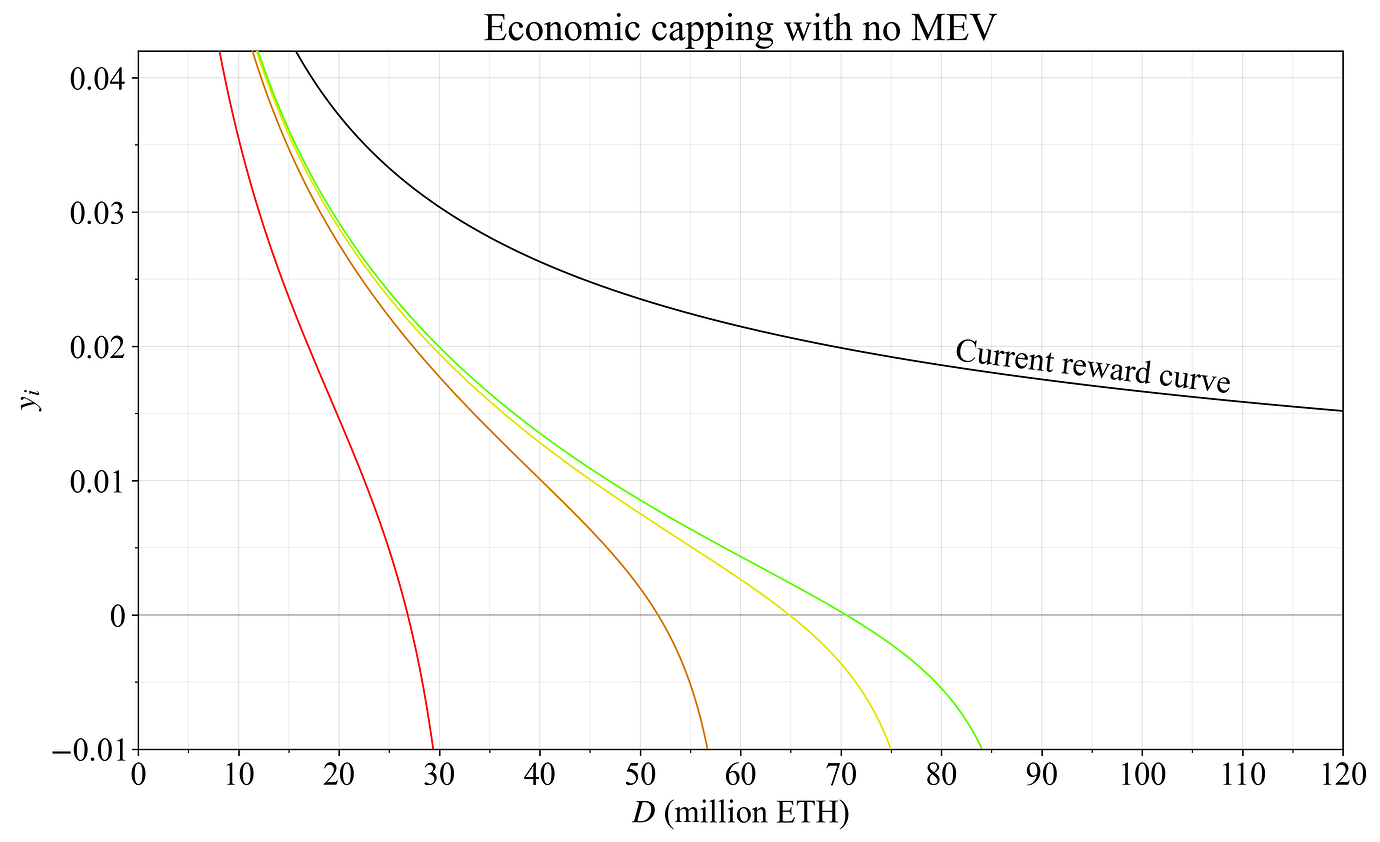 \
图 203196×1952 315 KB
\
图 203196×1952 315 KB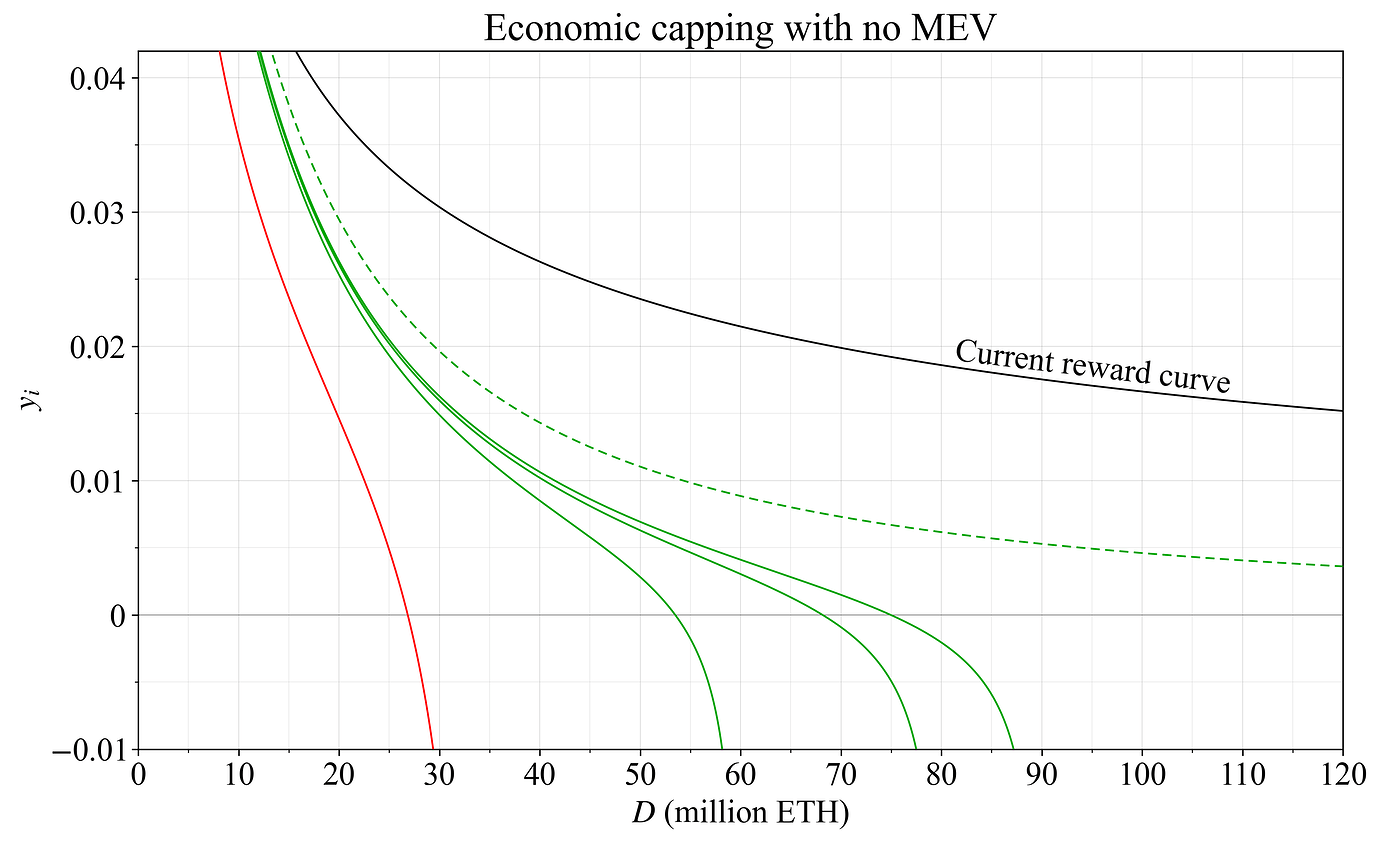 \
图 213196×1952 352 KB
\
图 213196×1952 352 KB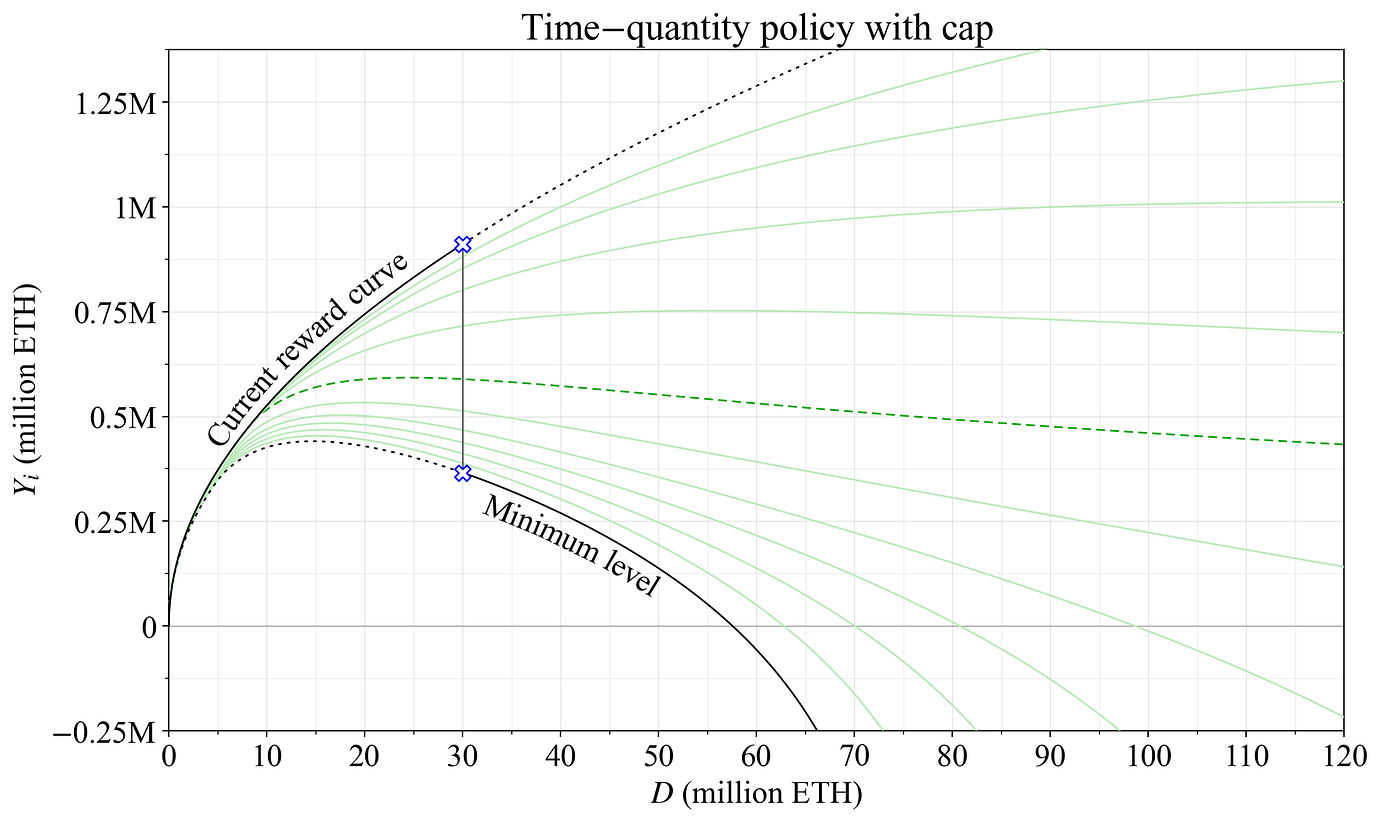 \
图 222184×1304 303 KB
\
图 222184×1304 303 KB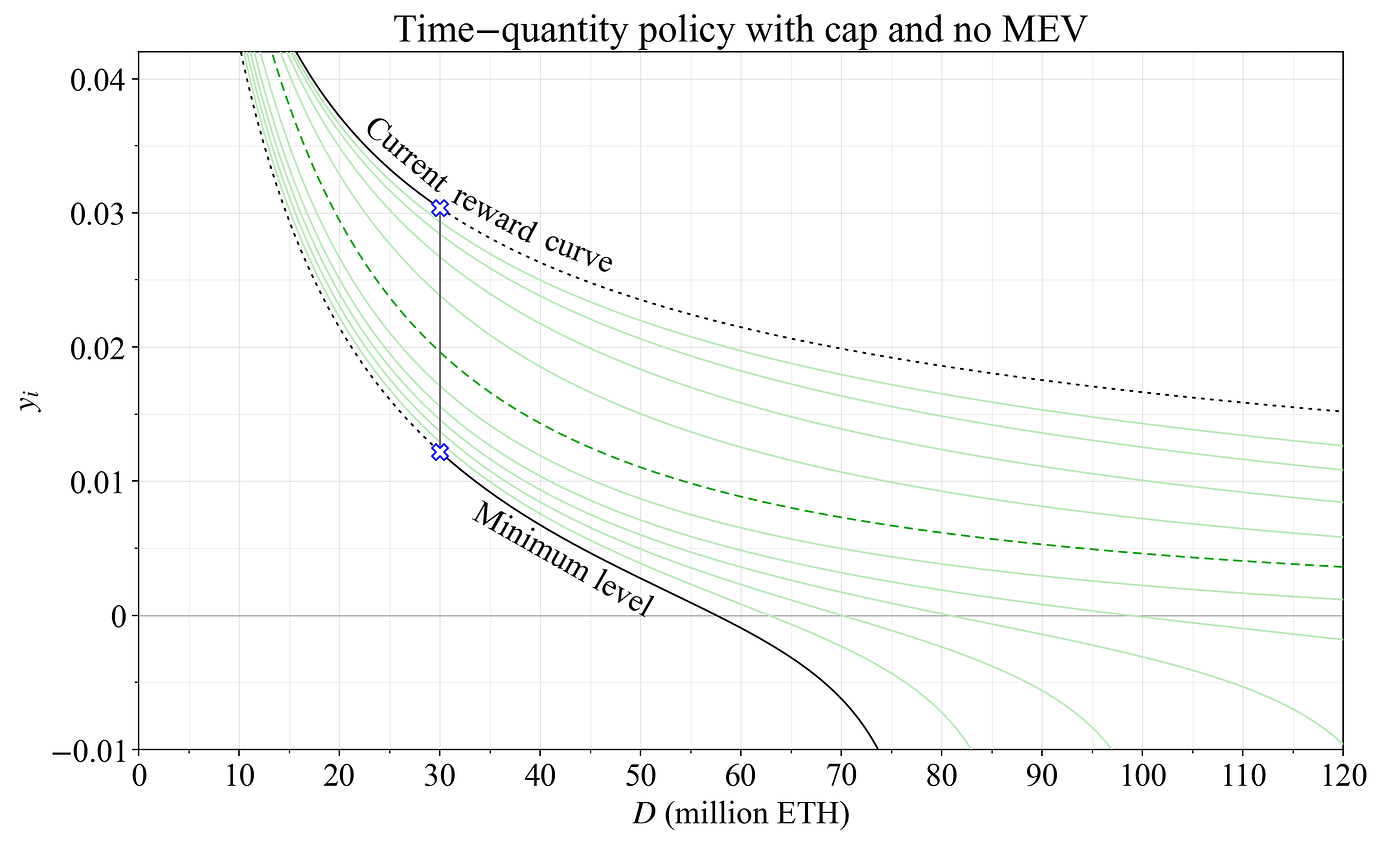 \
图 232131×1304 370 KB
\
图 232131×1304 370 KB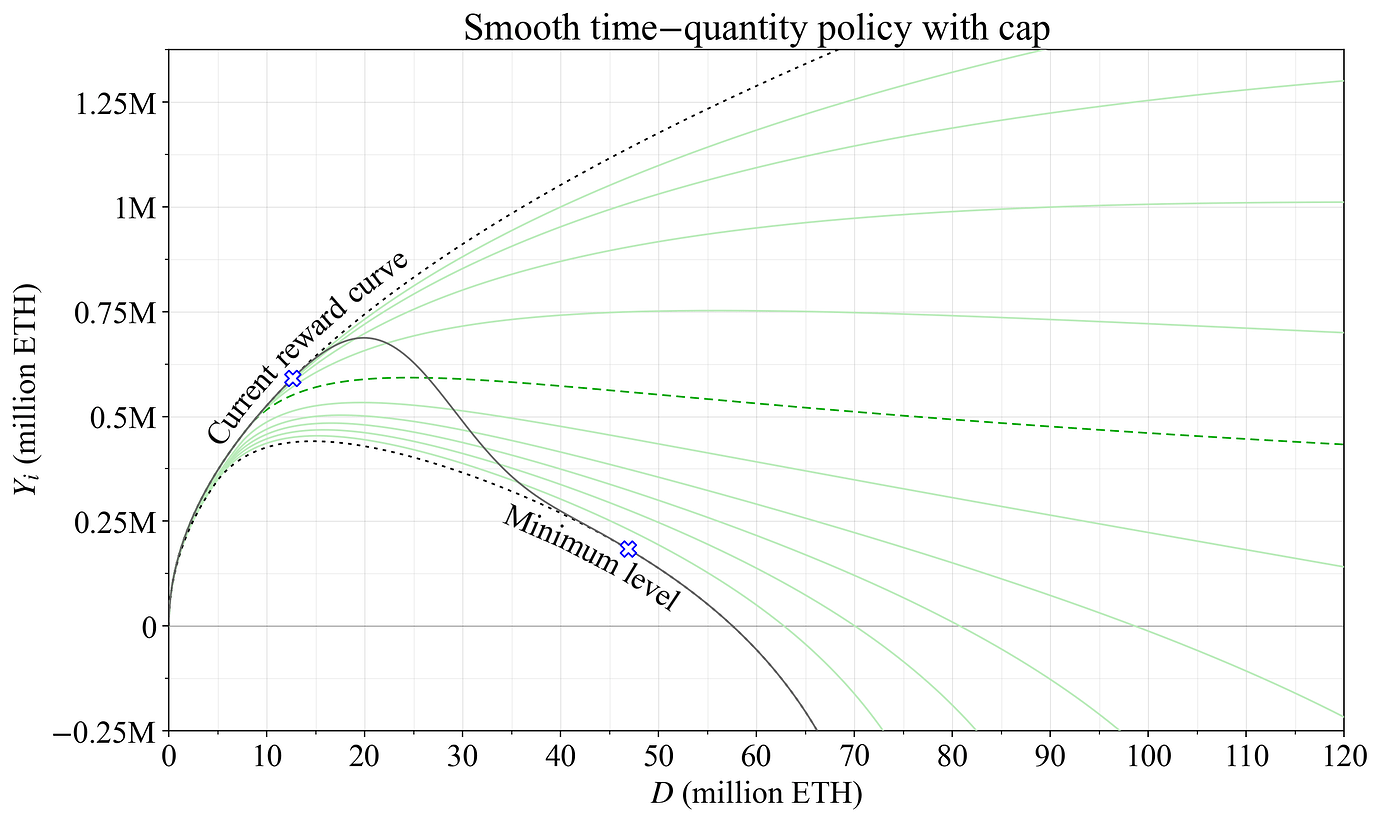 \
图 242184×1304 307 KB
\
图 242184×1304 307 KB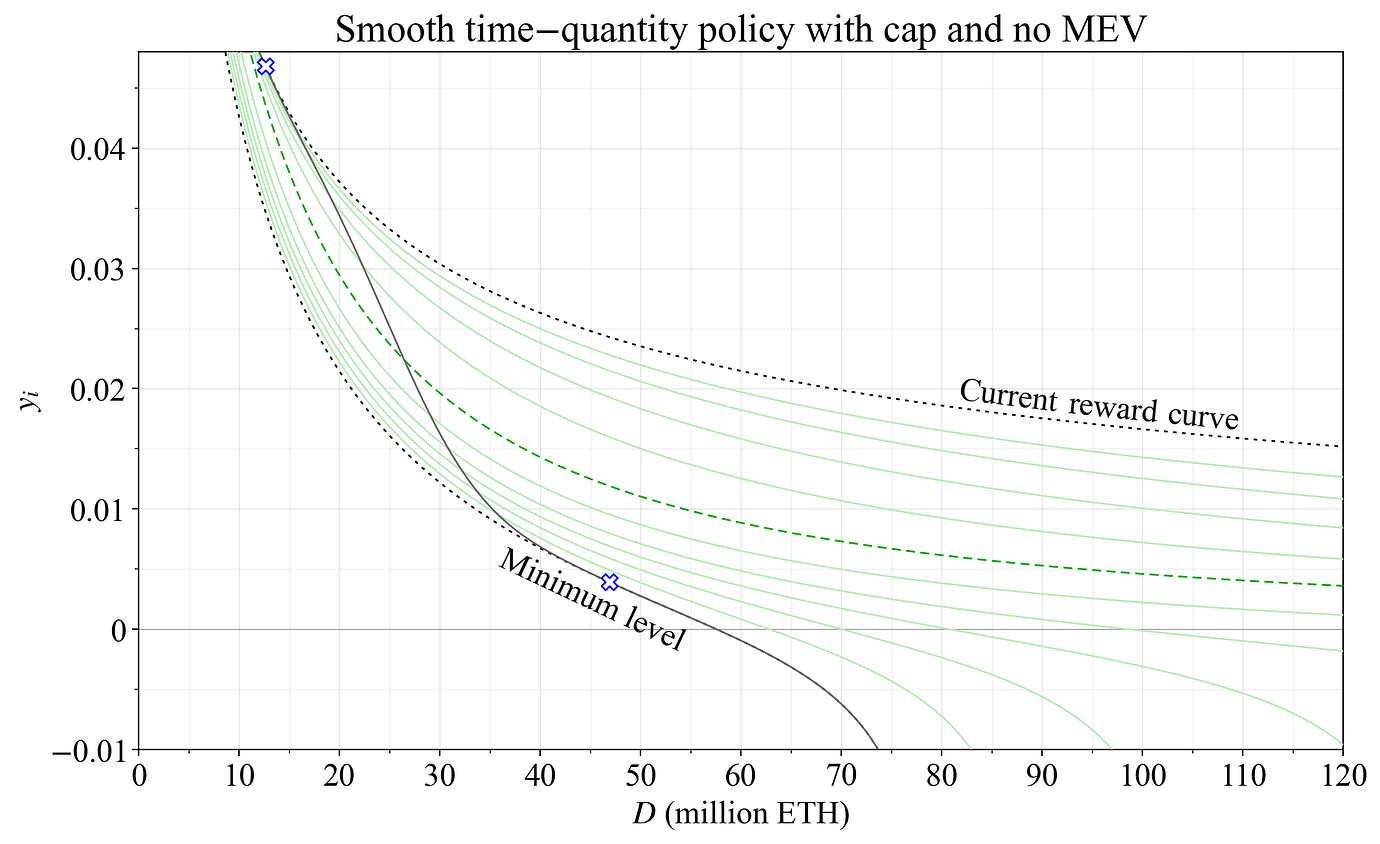 \
图 252131×1304 369 KB
\
图 252131×1304 369 KB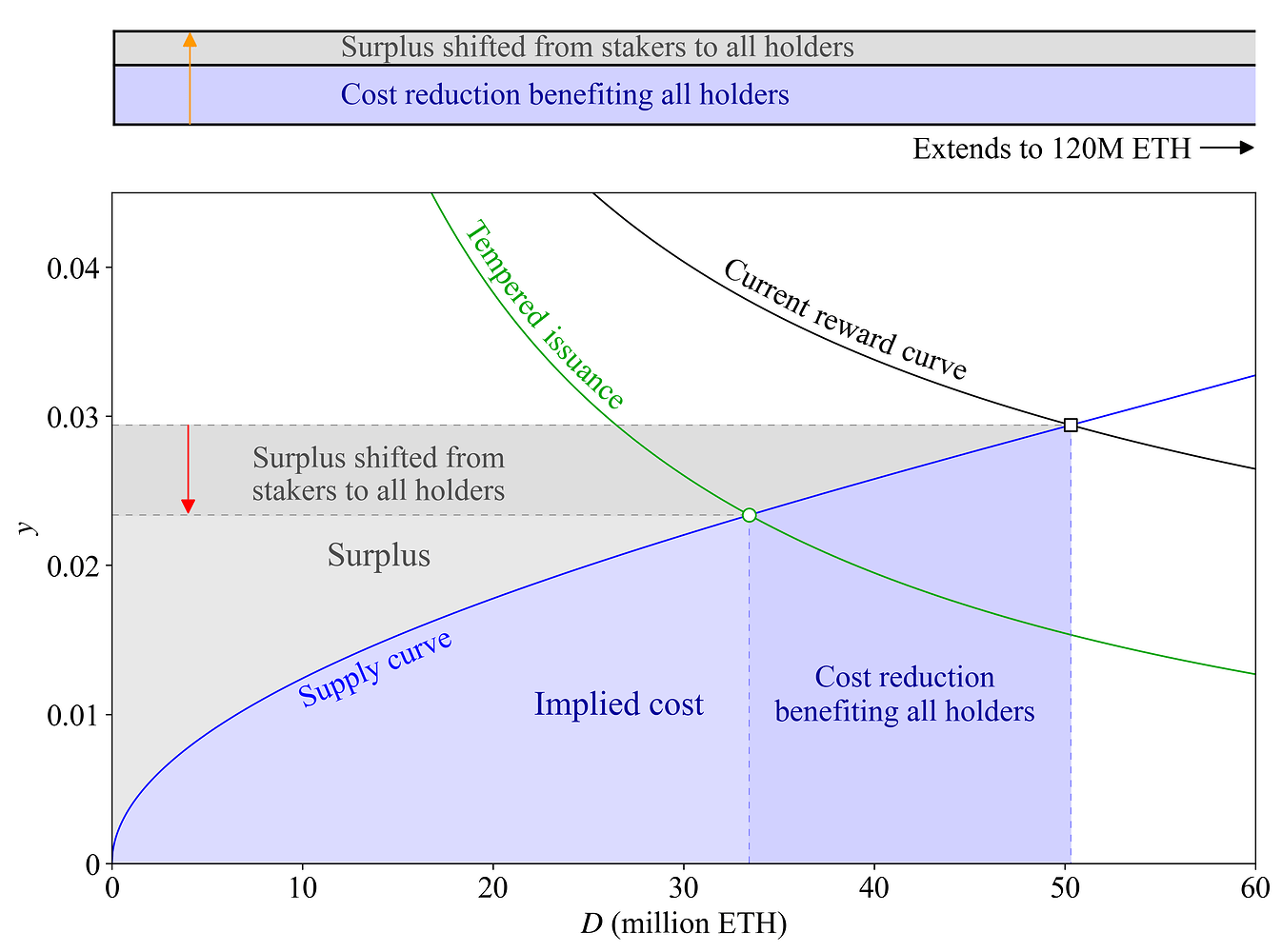 \
Figure 263341×2479 483 KB
\
Figure 263341×2479 483 KB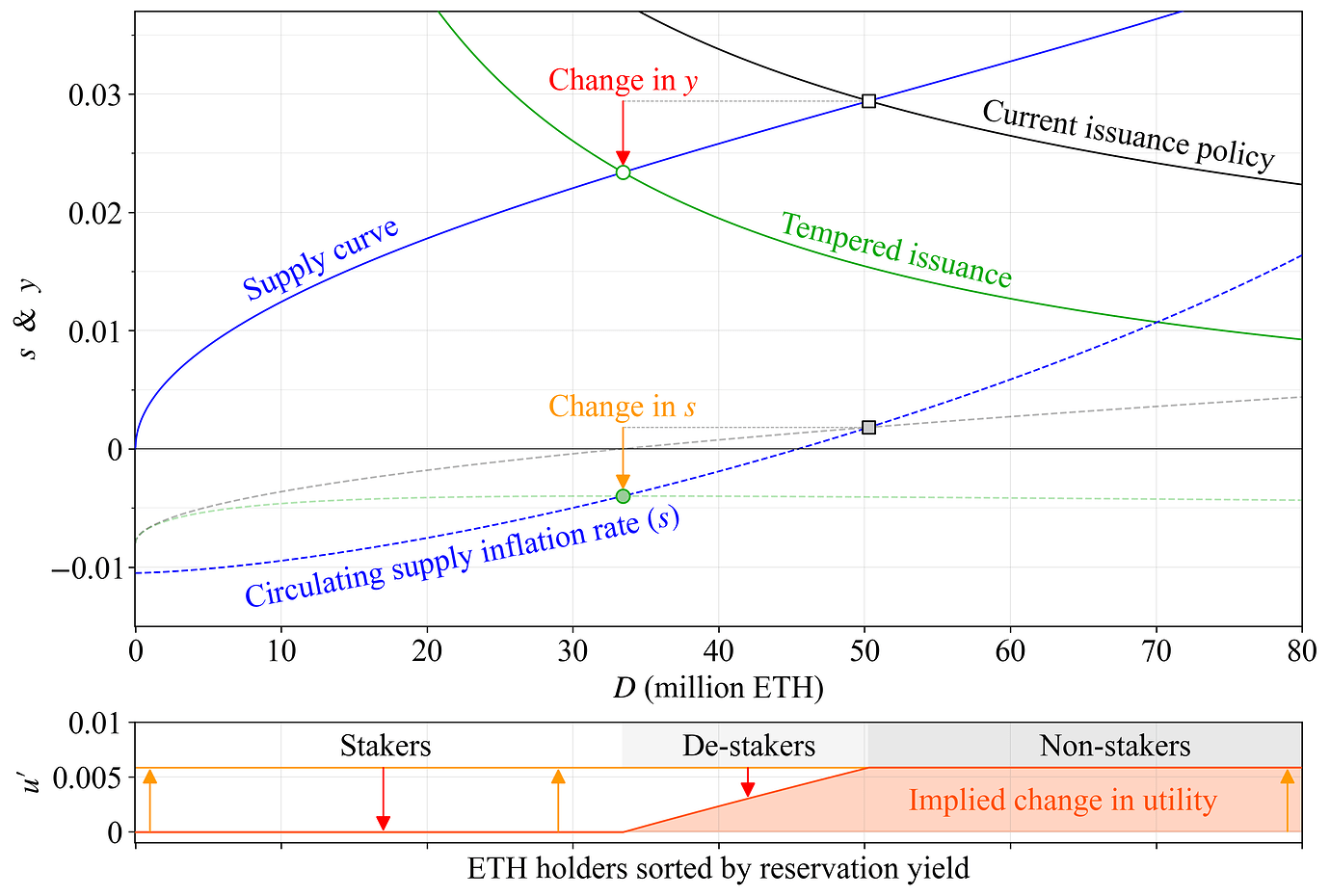 \
Figure 273179×2146 486 KB
\
Figure 273179×2146 486 KB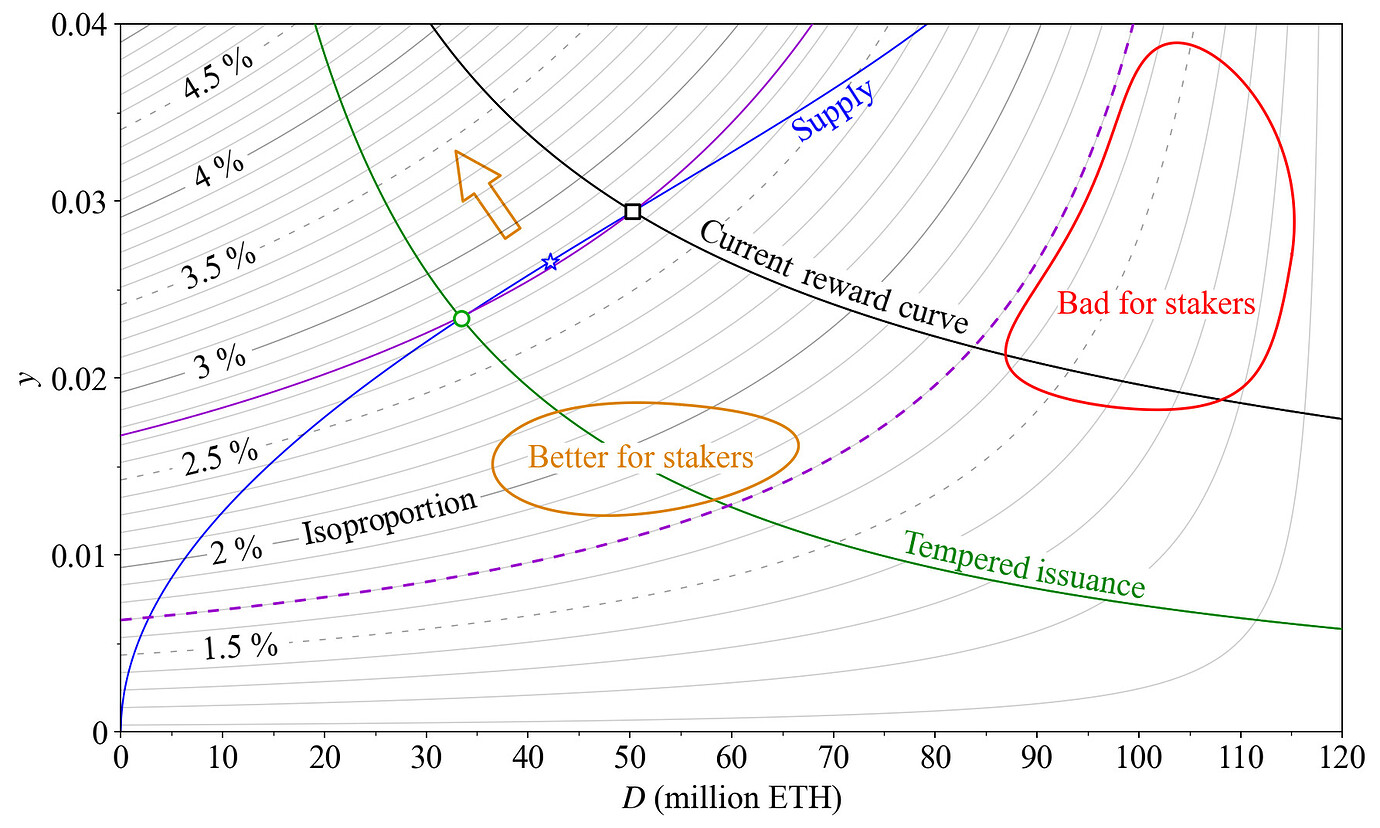 \
Figure 281786×1073 323 KB
\
Figure 281786×1073 323 KB
