以太坊 WHIR：zk-s[nt]arks

作者： Thomas Coratger, Giacomo Fenzi

感谢 Justin Drake 和 Tom Wambsgans 提供的深刻且富有建设性的反馈。

介绍：为什么以及如何在未来将 WHIR 用于以太坊？

随着以太坊的持续扩展，对 SNARK 证明系统的要求变得越来越迫切：证明必须非常小，验证必须非常快，并且整个系统必须保持足够的简单和健壮性，以便在最小的硬件上进行验证——理想情况下，就像 Raspberry Pi Pico 2 这样受限的设备，正如 Justin Drake 最近在 Ethproofs call n°2 中所建议的那样。在这种背景下，一个应用脱颖而出，成为了下一代 SNARK 的试验场：以太坊即将推出的精简链的签名聚合。它捕捉到了正确的约束条件——高吞吐量、严格的延迟、最小的验证成本、后量子环境——并且将在本文中作为一个运行示例。

这些需求正在推动证明系统的一个更广泛的趋势：从单变量到多线性多项式表示的转变。然而，在多线性环境中工作需要新的工具——特别是对于邻近性测试，像 FRI (Fast Reed-Solomon Interactive Oracle Proof of Proximity) 这样的协议不再那么出色。这就是 WHIR 的用武之地。WHIR 是一种递归的、基于哈希的邻近性测试协议，用于受约束的里德-所罗门码。它被设计为在单变量和多线性模式下都能高效运行，使其足够灵活，适用于各种证明系统。WHIR 的核心结合了两个优雅的想法：一个递归折叠机制（灵感来自 STIR），逐轮压缩域，以及一个轻量级的基于 sumcheck 的约束检查（类似于 BaseFold），以最小的开销确保代数正确性。

其结果是一个体现简洁性的工具——这是以太坊的关键属性——通过提供小的证明（通常在 100 KB 以下，且具有 128 位的安全性，假定里德-所罗门码具有高达容量的相互关联一致性）、快速验证（通常在 1 毫秒到几毫秒之间，取决于所选择的哈希函数）和低内存使用量，同时仅依赖于基于哈希的密码学假设。WHIR 支持紧凑、低 gas 的 SNARK，能够实现高效的签名聚合，并为验证者简单性至关重要的系统中的递归证明铺平了道路。

在本文的其余部分，我们将详细介绍 WHIR 的工作原理、为什么它很重要，以及它如何帮助塑造以太坊上高效证明系统的未来。

关于现代 SNARK 的一些背景知识

现代 SNARK 通常通过在多项式承诺方案（PCS）之上分层多项式交互式 Oracle 证明（PIOP）来构建。一个常见的例子是 AIR（代数中间表示）模型，其中证明者通过将表的每一列编码为单变量多项式来承诺执行轨迹。这种策略虽然简单，但引入了可扩展性瓶颈：每一列都变成一个单独的多项式，导致大的证明大小和昂贵的验证——当涉及数百列时，通常达到兆字节的量级。

为了克服这一点，最近的证明系统正在从单变量表示转向多线性表示。不再单独承诺每一列，而是将整个 witness 编码为单个多线性多项式。这种改变提供了几个优点：更好的压缩、更简单的约束表达，以及证明大小取决于轨迹的总表面积，而不是其形状。像 Binius、Jolt 和 SP1 Hypercube 这样的系统已经接受了这一趋势——其中 SP1 是第一个展示以太坊区块实时证明的系统，它使用了多线性承诺。

在这种多线性设置中，约束验证可以使用 sumcheck 协议来完成，而不是构造和评估商多项式。Sumcheck 提供了更好的模块化，并且可以与多线性编码无缝协作，尽管在使用小域时会带来性能上的权衡。最近，“单变量跳跃”优化 解决了这个限制，它通过在基本域内完全折叠多个变量来加速 sumcheck。通过在一个廉价的基本域中预先完成更多的工作，单变量跳跃减少了后期回合中昂贵的扩展域评估，从而在不牺牲健全性的情况下显着提高了证明者的速度。除了这种方法之外，还在探索加速 sumcheck 协议的其他方法。值得注意的最新研究方向是 S. Bagad 及其合作者 提出的方法。

在这个新的堆栈中，WHIR 扮演着关键的角色：它执行邻近性测试步骤，验证承诺的多线性函数是否确实接近有效的码字。

WHIR 如何工作？

本节对 WHIR 的运作方式进行了直观而严谨的解释，重点介绍了其核心机制，而没有深入研究完整的形式化证明。目标是为工程师提供清晰易懂的理解。

里德-所罗门码邻近性测试

从高层次上讲，WHIR 是一种验证函数$ f : \mathcal{L} \to \mathbb{F}$ 是否“接近”低阶多项式的工具——并且该多项式满足一些代数约束。

什么是里德-所罗门码？

里德-所罗门码是源自在有限域上评估低阶多项式而产生的函数集。更准确地说，假设我们选择一个有限域 $\mathbb{F}$ 和一个子集$ \mathcal{L} \subseteq \mathbb{F}$，称为求值域。次数为 d 的里德-所罗门码是：

\mathrm{RS}[\mathcal{L}, d] = \left{ f : \mathcal{L} \to \mathbb{F} \ \middle|\ f(x) = \hat{f}(x)\ \text{对于某个多项式 } \hat{f} \text{，其 } \deg(\hat{f}) < d \right}.

换句话说，这些只是域 \mathcal{L} 上次数小于 d 的多项式的所有可能的求值表。当我们说函数 f “在码中”时，我们的意思是它与这样的多项式一致。当 f “接近”码时，我们的意思是它在 \mathcal{L} 中的大多数点上与某个码字一致——这被称为邻近性。

为什么我们关心邻近性测试？

在证明系统中，证明者可能会向验证者发送一个看起来像在评估低阶多项式的函数 f——但实际上可能不是。为了确保健全性，验证者必须检查 f 是否接近里德-所罗门码中的真实码字。这是邻近性测试的核心。

多线性视角和平滑码

WHIR 使用的是 RS 码的更结构化的版本。它不使用任意多项式，而是使用多线性的多项式——也就是说，每个变量的次数最多为 1 的多项式。例如，在变量 x、y、z 中，多线性多项式可能看起来像 3 + 2x + 5y + 7xz，但不能是 x^2 或 y^2z。

为此，WHIR 假设：

• 域 \mathcal{L} 是 \mathbb{F}^* 的一个乘法子群，其大小是 2 的幂,
• 次数界 d 也是 2 的幂，比如 d = 2^m。

在这些条件下，任何次数小于 2^m 的单变量多项式 \hat{f} 都可以唯一地被视为 m 个变量的多线性多项式。原始多项式在点 x \in \mathcal{L} 处的求值等同于在其新的多线性对应物（我们也称之为 \hat{f}）在从 x 导出的特殊向量处求值。这给了我们以下优雅的重新解释：

f(x) = \hat{f}(\mathrm{pow}(x, m)), \quad \text{其中 } \mathrm{pow}(x, m) = (x^{2^{0}}, x^{2^{1}}, \dots, x^{2^{m-1}}).

这种转换将简单单变量域 \mathcal{L} 中的每个点映射到 m 维布尔超立方体上的一个点。它允许我们应用高效的多线性技术（如 sumcheck 协议），同时保留原始代码结构的简单性。

向代码添加约束

在许多协议中，我们不仅要检查 f 是否接近一个多项式——我们还要确保这个多项式满足特定的代数条件。例如，我们可能想要强制执行：

\hat{f}(r) = y \quad \text{或更一般地} \quad \sum_{\mathbf{b} \in {0,1}^m} \hat{w}(\hat{f}(\mathbf{b}), \mathbf{b}) = \sigma,

其中 \hat{w} 是一个固定的约束多项式，\sigma 是一个已知值。

为了表达这一点，WHIR 使用了 RS 码的一个变体，称为 受约束的里德-所罗门码。形式上，我们定义：

\mathrm{CRS}[\mathcal{L}, m, \hat{w}, \sigma] := \left{ f = \hat{f}|_\mathcal{L} \ \middle| \ \sum_{\mathbf{b} \in {0,1}^m} \hat{w}(\hat{f}(\mathbf{b}), \mathbf{b}) = \sigma \right},

其中 f 是在 \mathcal{L} 上对多线性多项式 \hat{f} 的求值。

这个约束确保 f 不仅来自一个多项式——而且是满足特定代数恒等式的多项式。

折叠问题：递归压缩

为了使邻近性测试高效，WHIR 应用了一种称为 折叠 的递归压缩技术。受到 FRI 和 STIR 等协议的启发，折叠逐渐将一个大的问题简化为一个更小的、等价的问题。每一轮都会缩小函数的域和复杂性，同时保留其基本属性，从而使最终的检查对验证者来说变得容易。经过足够的回合后，问题变得非常小，可以直接且廉价地检查。

WHIR 回合：结合折叠和 Sumcheck

这个过程中的核心操作是折叠，最好通过直观的交错里德-所罗门解释来理解。我们可以将域 \mathcal{L} 视为被分组为小块，而不是一个复杂的递归公式。证明者在每个块中的数据定义了一个小的、局部多线性多项式。然后，折叠整个块就像在验证者的随机质询 \alpha 处评估这个局部多项式一样简单。

在数学上，如果我们让 p_y(X_1, \dots, X_k) 成为与新的、更小域中的点 y 对应的点的块的局部多项式，则折叠操作仅为：

\mathrm{Fold}_k(f, \alpha)(y) = p_y(\alpha_1, \dots, \alpha_k)

这种使用随机质询向量 \alpha \in \mathbb{F}^k 的单一评估，优雅地将来自原始块中 2^k 个点的信息压缩为一个新函数的单一值。

WHIR 有力地增强了这个想法。在一轮中，它使用一个 k 维的随机质询 \alpha，通过将其并行应用于两个过程来一次消除 k 个变量：

• 一个 k 轮的 Sumcheck 将主要的代数约束简化为一个新的、更简单的约束。
• 折叠（作为局部评估） 将函数本身简化为一个更小的函数。

整个回合将原始的邻近性实例转换为一个明显更小的实例，其中约束多项式 \hat{w} 和目标 \sigma 都被更新：

f \in \mathrm{CRS}[\mathbb{F}, \mathcal{L}, m, \hat{w}, \sigma] \quad \xrightarrow{\text{一轮 WHIR}} \quad f' \in \mathrm{CRS}[\mathbb{F}, \mathcal{L}^{(2)}, m-k, \hat{w}', \sigma']

这带来了关键的效率提升。虽然我们将变量的数量减少了 k（将多项式空间缩小了 2^k 倍），但评估域仅减半。这显着提高了码率$ \rho = 2^m / |\mathcal{L} |$。新的码率 $\rho' $由下式给出：

$\rho' = 2^{1-k} \rho$

2^{-k} 项来自减少消息空间（减少多项式系数），而 2^1 项来自仅将域大小减半。在每一轮中降低码率是 WHIR 低查询复杂度的关键原因。

折叠的健全性保证

折叠过程经过精心设计，以保证健全性和鲁棒性，这对于整个证明系统的安全性至关重要。

• 折叠保留了函数与代码的距离。如果一个函数从任何有效码字开始就相距甚远，那么在折叠后它仍然遥远。错误无法被代数混合隐藏或抵消。
• 在列表解码设置中，多个有效的码字可能接近证明者的函数。折叠保证（以高概率）将附近的码字完整地映射到新的、更小的问题。在递归期间不会引入虚假或错误的解决方案，从而确经验证者不会被误导。

WHIR 迭代总结

每个 WHIR 迭代，如下图所示，都会将一个邻近性测试问题简化为一个更小的问题，同时保持健全性。

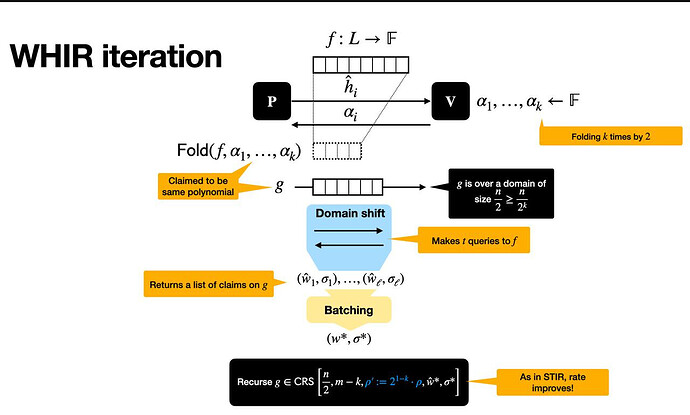
这发生在三个主要阶段：

设置

我们从一个函数 f : \mathcal{L} \to \mathbb{F} 开始，该函数定义在一个结构化的域 \mathcal{L} 上（大小为 2^m 的乘法子群）。证明者声称 f 来自评估一个多线性多项式 \hat{f}，并且该多项式满足一个约束，例如：

\sum_{\mathbf{b} \in {0,1}^m} \hat{w}(\hat{f}(\mathbf{b}), \mathbf{b}) = \sigma,

其中 \hat{w} 是一个简单的约束多项式。这是我们要验证的核心声明。

交互阶段

验证者发送一个随机质询 \alpha，指示证明者折叠该函数——通过隐藏一个变量将两个输入压缩为一个。这产生了新的函数 f' = \mathrm{Fold}(f, \alpha)，该函数定义在较小的域 \mathcal{L}^{(2)} 上，并且涉及 m - 1 个变量而不是 m 个变量。

为了确保折叠是诚实地完成的，验证者执行几个检查：

• 它在域外采样一个随机点，并要求证明者对其进行评估，从而确保 f' 确实来自一个低阶多项式。
• 它从折叠函数中采样一些值，并将它们与 f 应该说的值进行比较，从而强制执行一致性。
• 它使用随机线性组合将所有这些检查（以及约束）组合成一个等式，并为下一轮准备一个新的约束多项式。

递归声明

在该回合结束时，验证者和证明者就一个新的声明达成一致：f' 接近一个较小域和较少变量上的新多项式 \hat{f}'，并且 \hat{f}' 满足一个新的约束：

\sum_{\mathbf{b} \in {0,1}^{m-1}} \hat{w}'(\hat{f}'(\mathbf{b}), \mathbf{b}) = \sigma'.

这个新实例与原始实例具有完全相同的形式，只是更小。然后，WHIR 在此声明上递归，重复相同的步骤，直到函数足够小以可以直接检查为止。

这种方法的美妙之处在于，每一轮可以一次剥离 k 个变量，同时仅将域缩小 2 倍，从而降低码率。最后，验证者有很高的信心，原始函数 f 接近一个满足约束的有效码字——所有这些都只需很少的努力。

WHIR 可以为以太坊提供什么

WHIR 与众不同之处在于它执行邻近性检查的方式。WHIR 没有依赖 FRI 等传统技术，而是使用了一种基于 折叠 加上 Sumcheck 的递归方法，这使得它在多线性设置（其中 witness 是 {0,1}^m 上的函数）中特别有效。这种设计实现了几个特别与以太坊和类似的链上环境相关的优势。

• 极低的查询复杂度。 WHIR 仅需要少量的查询即可执行邻近性测试。这意味着更少的 Merkle 树打开（Merkle openings），更少的链上数据发送，并最终降低验证成本。

• 快速验证，通常在微秒到低毫秒范围内。 WHIR 专为超快速验证而设计——当使用像 Keccak 或 Blake3 这样的快速哈希函数时，通常在几百微秒内，当使用像 Poseidon2 这样的 SNARK 友好型哈希函数时，通常在几毫秒内。它通过结合两个强大的理念来实现这一点：BaseFold 的 Sumcheck 协议，它以最小的开销验证多项式恒等式；以及 STIR 的递归折叠，它在每一轮中压缩问题大小。总之，它们将全局邻近性检查变成一系列易于验证的较小检查。

• 更小的证明。 WHIR 显着减少了证明大小，尤其是在多线性设置中。WHIR 允许将整个 witness 表示为单个多线性多项式 \hat{f}，而不是将跟踪的每一列作为单独的单变量多项式提交。只需要一个承诺，递归折叠逐轮减少该域的大小。这导致更少的承诺、更少的查询和更少的编码开销，即使对于大型计算，也可以显着减小证明。

• 灵活的编码。 WHIR 支持单变量和多线性编码。这使其与各种 SNARK 构造兼容——无论它们是使用传统的单变量编码（如基于 PLONK 或 FRI 的系统），还是多线性方法。

在以太坊上的应用

凭借其紧凑的证明和微秒级的验证，WHIR 特别适合以太坊应用程序：

• Rollups。 Rollups 中的状态转换可以编码为多线性多项式。WHIR 帮助紧凑地证明这些转换，并为以太坊 L1 验证器提供极快的验证。
• 签名聚合： 随着未来需要后量子 BLS 签名替代品，高效验证数千个基于哈希的签名至关重要。WHIR 提供了密码学引擎，将这些大型集合压缩为单个、恒定大小的证明，并具有最小的链上验证占用空间。
• 低 Gas 的 SNARK 验证: 链上 Gas 成本主要由数据存储和计算决定。WHIR 通过最小化其查询复杂度（减少 Merkle 路径数据）及其验证者的计算工作来解决这两个问题。虽然某些预量子 SNARK 仍然经过高度优化，但 WHIR 的性能使其成为后量子系统的领先竞争者，在后量子系统中，链上效率是不可谈判的，如 这篇研究文章 中探讨的那样.

简而言之，WHIR 是一种快速、递归且灵活的临近性协议，可以自然地融入现代 SNARK 堆栈中。对于以太坊来说，它提供了一条通往更小、更便宜和更快的证明的途径——尤其是在已经受益于多线性编码的系统中。

WHIR 与 FRI：邻近性测试的一代飞跃

FRI 一直是现代证明系统的基石，尤其是 STARK。它的设计使用递归折叠来有效地测试承诺函数是否接近低阶多项式。在经典的 STARK 流程中，你首先将所有代数约束组合成一个单一的、高阶的“组合多项式”，然后你在其上运行 FRI 以证明它实际上是预期阶数的低阶多项式。这种方法非常强大，并建立了具有对数多项式验证器的后量子证明的可行性。

但是，SNARK 设计的格局正在转变。像 Jolt、Binius 和 SP1 Hypercube 这样的现代系统正在弃用这种两步“组合然后测试”模型，转而采用更集成的多线性方法。在这种新范式中，证明是围绕 Sumcheck 协议构建的，Sumcheck 协议是一种用于验证多线性多项式上的声明的工具。这是 WHIR 代表根本演变的地方。

WHIR 重新思考了这个现代的、Sumcheck 原生的世界的邻近性测试。与运行 后处理约束的通用低阶测试不同，WHIR 将约束验证直接集成到其递归过程中。FRI 回合大致包括折叠域和在随机点上执行一致性检查。相反，WHIR 回合将此折叠与轻量级的 Sumcheck 相结合，这不仅确保了折叠的正确性，而且还将计算的代数约束转移到下一个较小的实例。

这种架构差异带来了关键的性能优势：

• 渐近线更少的查询。 这是 WHIR 最大的优势。对于具有 2^m 个元素的计算，FRI 的查询复杂度随 m 线性增长，而 WHIR 的查询复杂度随 m 对数增长。对于大规模计算，这是一个巨大的改进。在实践中，这意味着更少的 Merkle 路径打开，这是证明大小和链上验证 Gas 成本的主要驱动因素。

• 原生多线性和约束支持。 WHIR 是 约束的里德-所罗门码的 IOP 邻近性。它旨在处理定义现代证明系统的多线性多项式和基于 Sumcheck 的关系。虽然 FRI 可以适应这些设置，但 WHIR 将它们视为一等公民，从而产生更清洁、更高效的设计。

• 非常快的验证。 更少的查询和轻量级的、基于 Sumcheck 的验证器逻辑的结合使得 WHIR 能够实现数百微秒的验证时间。这使其非常适合链上应用，因为每微秒的验证器工作都会直接转化为用户成本和网络吞吐量。

签名聚合：WHIR 的一个具体用例

以太坊未来共识层面临的关键挑战之一是寻找 BLS 签名的后量子替代品。已经探索了几种提案——包括 基于格的方案 和基于累积的协议——但其中许多方案都在努力平衡可扩展性、效率和后量子安全性。

一个特别有希望的方向是使用 XMSS 签名，该签名本质上是基于哈希的并且具有量子安全性。但是，XMSS 签名很大且单独验证成本很高，因此聚合变得至关重要。这个想法是使用基于哈希的 SNARK 将数千个单独签名压缩为单个简洁的证明，然后将其发布在链上。如 这篇以太坊研究文章 中所述，此类协议必须支持两个操作：

• 聚合（Aggregate）： 将一大批原始签名压缩为一个 SNARK 证明；
• 合并（Merge）： 将两个现有的聚合证明递归地组合成一个证明。

合并操作引入了递归证明要求——而这正是 WHIR 的闪光点。得益于其折叠机制和最小的查询复杂度，WHIR 使得构建小且易于验证的 SNARK 变得更加容易。更少的查询意味着更少的哈希评估，从而直接降低了验证每一层递归的成本。与 FRI 等传统 PCS 构造相比，WHIR 能够实现更快的递归证明——这是实时签名聚合的关键因素。

今天的表现，以及下一步

在这种情况下，衡量性能的一种自然方法是每秒可以证明的哈希数量（例如，Poseidon2）。我们当前的 WHIR 实现实现了：

• 在高端 GPU（RTX 4090）上 每秒 100 万个 Poseidon2 哈希。
• 在消费级 CPU 上 每秒 100,000 个 Poseidon2 哈希。

PCS 逻辑（WHIR-P3）和 PIOP 层（Whirlaway）都是公开的并且在积极优化。虽然当前的瓶颈是 CPU 性能，但正在进行的努力旨在达到与 GPU 速度相同的水平——目标是在 CPU 上达到每秒 100 万个哈希，与 Plonky3 等系统已经展示的水平相当。

总结和后续步骤

WHIR 提供了一种引人注目的新方法来进行邻近性测试，特别适合以太坊的需求：较小的证明大小、快速验证以及与单变量和多线性证明系统的无缝集成。其递归折叠策略和通过 Sumcheck 进行的约束检查机制使其非常适合现代 SNARK 堆栈，尤其是在效率和简单性至关重要的应用程序中——如 Rollups、zkVM 以及精简链的签名聚合。

在这篇文章中，我们将重点放在 WHIR 协议本身及其优势上。但是 WHIR 只是完整 SNARK 的一个组成部分。在以后的文章中，我们将描述如何围绕 WHIR 构建一个完整的证明系统，展示它如何融入完整的使用基于哈希的密码学的签名聚合流程中。

与此同时，我们正在积极优化我们的实现——目标是达到与当今最佳系统相匹配或超过的 GPU 和 CPU 证明速度，同时保持协议的模块化和易于采用。我们目前维护一个基于 Plonky3 的开源 WHIR 实现（WHIR-P3），并且我们计划将其直接上游到 Plonky3 作为社区驱动的努力。这符合我们使 WHIR 成为公共物品的愿景——开放、集体维护并且易于集成到其他项目中。

已经有几个从事 zkVMs 的团队表示有兴趣采用 WHIR，我们相信随着以太坊生态系统的发展，将会出现更多的用例。

我们的目标是使 WHIR 不仅仅是一个快速而优雅的想法——而是下一代链上证明的实用构建块。

• 原文链接： ethresear.ch/t/whir-for-...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～