RLNC内幕：P2P网络中加速广播的技术演练

随机线性网络编码 (RLNC) 不仅仅是一个学术概念，它是 Optimum 积极应用的一项技术，旨在突破区块链网络的限制。通过广播编码块而不是原始块，RLNC 减少了带宽浪费，并提高了数据传播的弹性。

“Optimum 是世界上第一个适用于任何区块链的高性能内存基础设施。在 RLNC 的支持下，它在速度、健壮性和吞吐量方面实现了数量级的提升。” — getoptimum.xyz

在本文中，我们将重点介绍 RLNC 的技术基础：它的工作原理、为什么它可以加速广播，以及一个带有示例代码的演练。在下一篇文章中，我们将探讨 Optimum 如何实现 Galois Gossip，这是一种由 RLNC 驱动的 gossip 协议，旨在超越当今的 GossipSub。注意：本文不仅适合初学者，也适合想要深入了解如何实现 RLNC 的工程师。

什么是随机线性网络编码 (RLNC)？

随机线性网络编码 (RLNC) 是一种使用线性代数 将数据编码成编码块 的方法。RLNC 不是将数据压缩成更小的尺寸，而是将原始块转换成多个代数混合。每个编码块本身看起来都像“乱码数据”，但是一旦一个节点收集到足够多的独立块，它就可以解码并重建原始数据。

这种方法确保节点不需要按顺序接收特定的数据块——任何足够的编码块集合就足够了。因此，RLNC 减少了广播中的带宽浪费，并使数据传播更能抵抗数据包丢失。

https://docs.getoptimum.xyz/docs/learn/overview/p2p

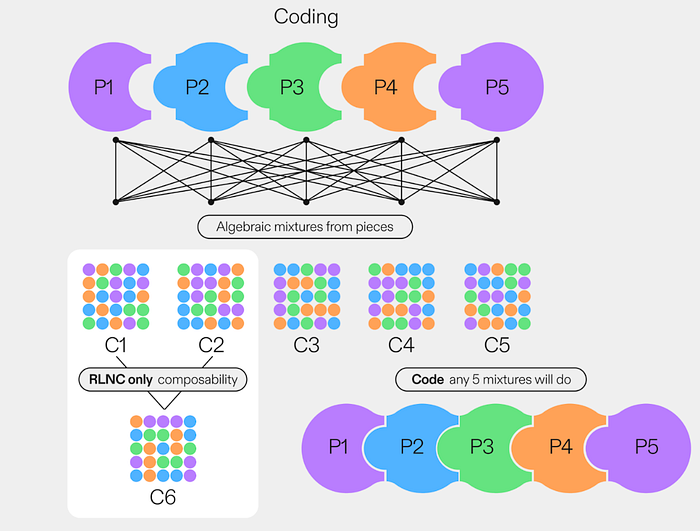
从高层次来看，RLNC 采用多个原始数据块（P1、P2、P3、P4、P5），并通过创建它们的代数混合来生成新的 编码块，即 C1、C2、C3、C4、C5。（C1 的大小小于原始数据）

有了 (C1, C2, C3, C4, C5)，你可以求解得到真实的据数（P1, P2, P3, P4, P5）。这里的可组合性意味着你可以从 (C1, C2) 组合创建 C6，然后使用 (C6, C2, C3, C4, C5) 求解数据。

让我们看一个例子，展示编码和解码是如何工作的：

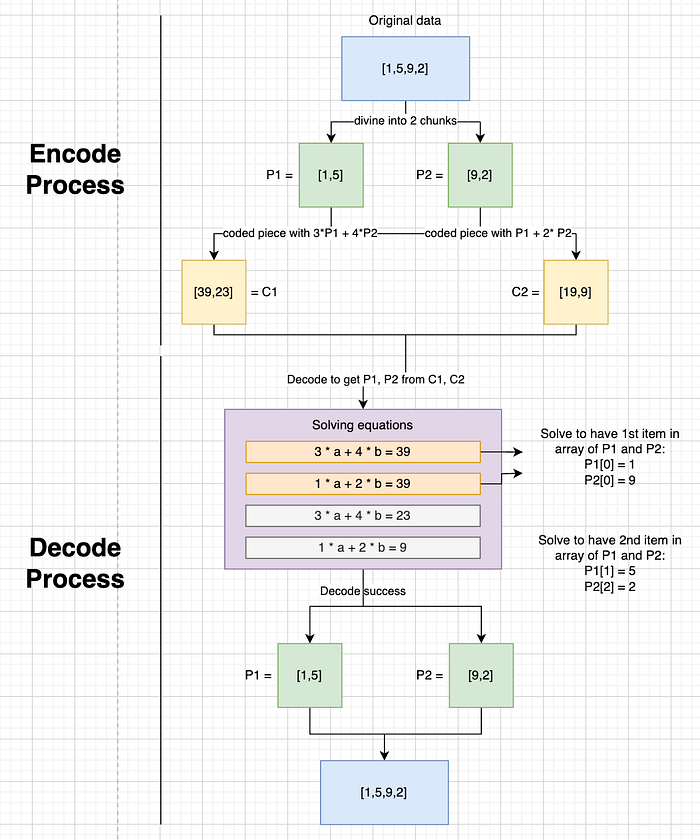
RLNC 中完整流程的编码和解码过程的示例

上图中示例的演练：

假设我们的原始数据是：

[1, 5, 9, 2]

为了简单起见，我们将其分成两块：

• P1 = [1, 5]
• P2 = [9, 2]

编码过程

我们不是直接发送 P_1 和 P_2，而是通过对它们进行线性组合来生成 编码块。例如：

• C1 = 3 * P1 + 4 * P2 = [1 * 3 + 4 * 9, 5 * 3 + 4 * 2] = [39, 23]
• C2 = 1 * P1 + 2 * P2 = [1 + 2 * 9, 5 + 2 * 2] = [19, 9]

现在，我们有两段 编码数据 [39, 23] 和 [19, 9] 以及两个 编码向量 [3,4] 和 [1,2]，而不是两段原始块。

编码向量 + 编码数据 构成 编码片 (编码数据包)。

解码过程

在接收端，节点想要重建原始的 P1 和 P2。块中的每个元素都给我们一个 线性方程组：

对于第一项：

• 3a + 4b = 39
• 1a + 2b = 19

对于第二项：

• 3a + 4b = 23
• 1a + 2b = 9

通过求解这些方程，接收器恢复： P1 = [1, 5], P2 = [9, 2]

最后，将两者结合起来，得到原始数组：

[1, 5, 9, 2]

重编码过程：

重编码过程是我在图像中没有提到的。但它实际上是用随机系数从编码块创建新的编码块。

当你创建 (C1, C2) 时，你可以通过以下方式创建 C3：

C3 = 2*C1 + C2 = [97, 47]

你也可以在 (C2, C3) 或 (C3, C4) ( C4 是另一个编码块) 之间求解以返回 P1, P2。

=> 是的，这就是 编码、解码、重编码 在 RLNC 中的工作方式。你只需要知道一个特性，那就是编码块之间是非“线性相关”的。

线性相关：

两个编码块之间的线性相关性将在示例中显示。如果你有两个方程：

• 2a + b = 5
• 4a + 2b = 10

从数学上讲，你无法解出这个方程，因为 2a + b 是“(4a + 2b) / 2”。

如果我们回到 编码过程，那么 [3,4] 和 [1,2] 是 编码向量。

• C1 = 3* P1 + 4* P2 => 编码向量 是 [3,4]
• C2 = 1* P1 + 2* P2 => 编码向量 是 [1,2]

由于 [3,4] 和 [1,2] 是 线性无关的，那么我们可以解出这个方程来得到 P1, P2。

编码块的大小：

在上面的例子中，它们并没有真正显示每个编码块的大小减少。

原始数据包 [1,5,9,2] 变成一个编码向量 [1,5] 和一个编码向量 [3,4]。如果你看看这个，大小几乎相同 LMAO。

=> 因为这是一个简单的演示示例。

假设原始数据包有 n 项，你将其分成 2 块。那么编码向量将有 (n/2) 项，编码向量将有 2 个项（系数）。

设 n = 1000，编码片（编码向量 + 编码向量）将具有大小 (n/2) + 2 = 502 项 => 大约减少 ~50% 的大小。

RLNC 在广播中有多好？

由于用语言不容易证明这一点。所以让我们看一个多播的例子，当一台计算机想要将它们的数据包广播到另外两台计算机时。

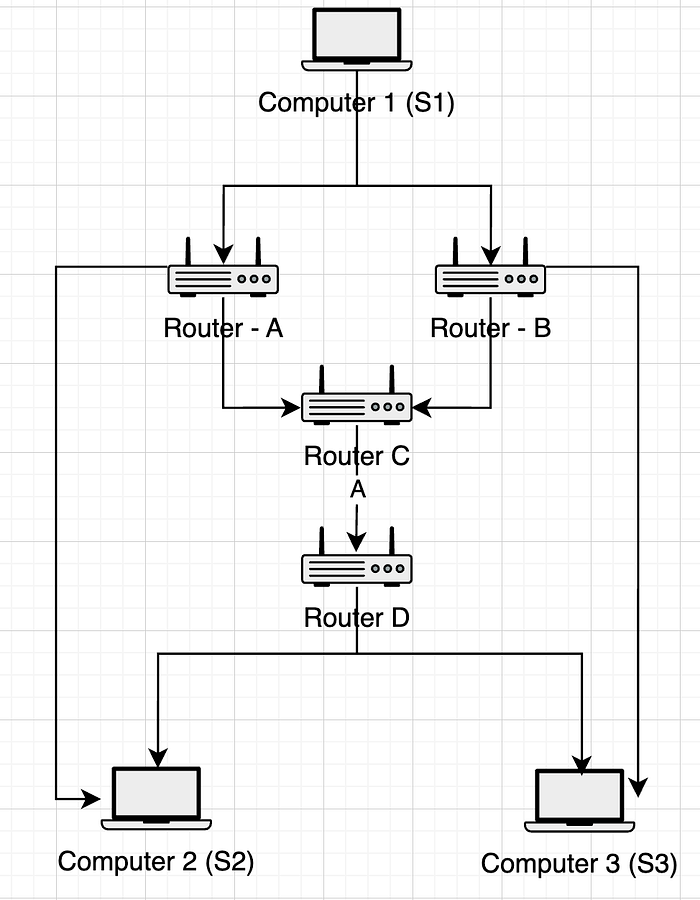
这里，让 S1 想通过 路由器 A、B、C 向 S2、S3 发送数据包。我们将以发送 完整数据包（普通）和发送 编码数据包（RLNC）为例。

完整数据包发送：

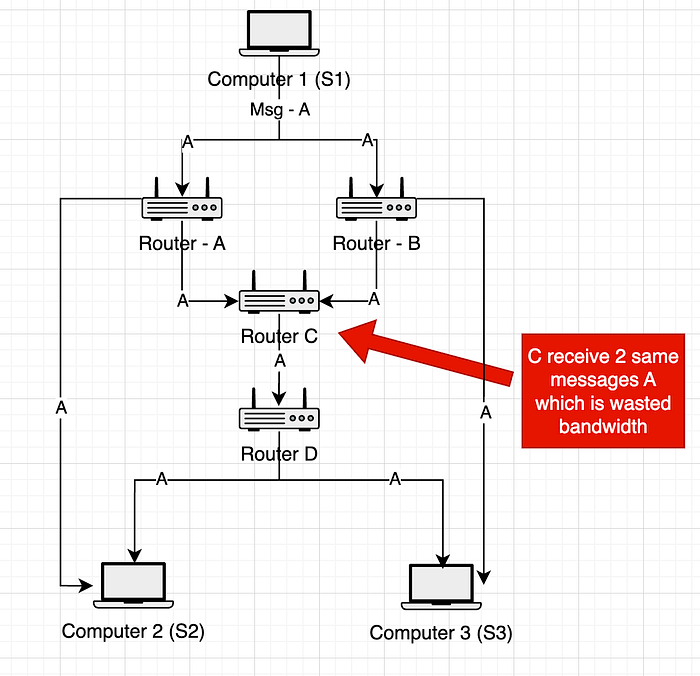
假设 S1 想要向 S2 和 S3 广播消息 A。消息 A 将发送到路由器 A、B、C、D。你可以看到，在路由器 C 和计算机 S2 以及计算机 S3 上，它们收到了两个相同的消息 A，这浪费了带宽。

=> 在此示例中，（C、S2、S3） 中有 3 * A (C, S2, S3) 浪费的带宽。

编码数据包发送 — RLNC：

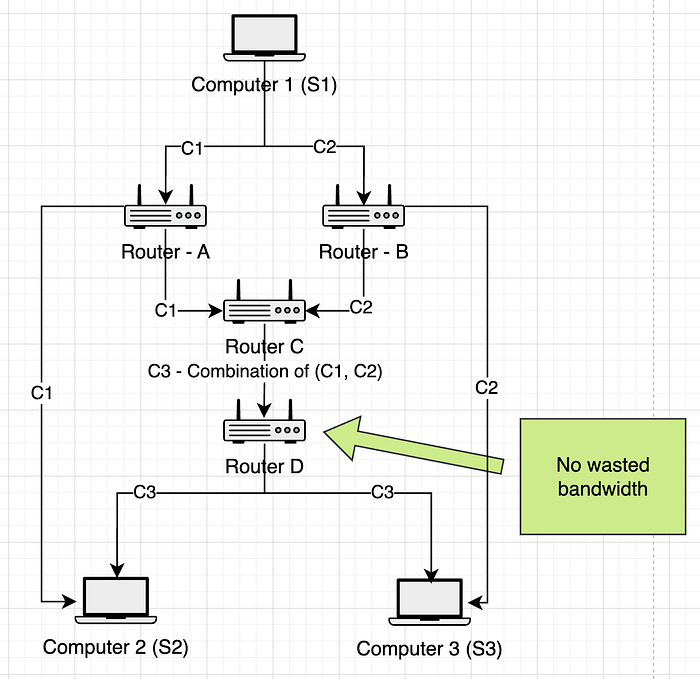
假设 S1 想要向 S2 和 S3 广播消息 A。消息 A 将创建两个编码块 C1、C2，，然后发送到路由器 A、B。当 C 接收到 C1、C2 时，它重新编码以创建 C3。

当计算机 S2、S3 分别收到 (C1, C3) 和 (C2, C3) 时。他们可以求解方程以返回原始数据。

如果我们将数据分成两个块用于此模型，则 C1、C2 的大小为 = 1/2 原始数据的大小。

=> 因此，没有浪费带宽。

=> 这是 RLNC 如何提高网络吞吐量和提高鲁棒性的示例。

注意：

在点对点网络中，有大量的验证器（以太坊 — 1000000 个节点）。

一个节点不能直接向 999999 个节点广播数据，它们会广播到它们的 mesh size（小型邻居）。

=> 我们将在下一篇文章中详细讨论，只需要想象整个 mesh 就像上面的例子一样。因此，OptimumP2P 将在节点之间带来更快的广播。

RLNC 编码实现演练

欢迎来到本编码演练部分！我将解释你在这里需要做的所有事情！

在编码中，你必须实现编码、解码和重编码过程的代码。

我们的代码是用 Rust 实现的。

编码器：

data 是你想要用来创建 编码块 的原始数据。

piece_count 是你想要分割 data 的块数。

piece_byte_len 是每个 编码块 的大小。

##[derive(Clone, Debug)]
pub struct Encoder {
    data: Vec<u8>,
    piece_count: usize,
    piece_byte_len: usize,
}

初始化函数：

pub fn new(mut data: Vec<u8>, piece_count: usize) -> Result<Encoder, RLNCError> {
    if data.is_empty() {
        return Err(RLNCError::DataLengthZero);
    }
    if piece_count == 0 {
        return Err(RLNCError::PieceCountZero);
    }

    let in_data_len = data.len();
    let boundary_marker_len = 1;
    let piece_byte_len = (in_data_len + boundary_marker_len).div_ceil(piece_count);
    let padded_data_len = piece_count * piece_byte_len;

    data.resize(padded_data_len, 0);
    data[in_data_len] = BOUNDARY_MARKER;

    Ok(Encoder {
        data,
        piece_count,
        piece_byte_len,
    })
}

此函数在编码之前准备原始数据。它将输入分成大小均匀的块，如果需要，添加填充，并插入一个特殊的边界标记，以便我们确切地知道解码后原始数据的结束位置。简而言之，它确保数据采用干净的、固定大小的格式，RLNC 编码器可以使用。

生成编码块函数：

pub(crate) fn code_with_coding_vector(&self, coding_vector: &[u8], coded_data: &mut [u8]) -> Result<(), RLNCError> {
    if coding_vector.len() != self.piece_count {
        return Err(RLNCError::CodingVectorLengthMismatch);
    }
    if coded_data.len() != self.piece_byte_len {
        return Err(RLNCError::InvalidOutputBuffer);
    }

    coded_data.fill(0);

    self.data
        .chunks_exact(self.piece_byte_len)
        .zip(coding_vector)
        .for_each(|(piece, &random_symbol)| gf256_mul_vec_by_scalar_then_add_into_vec(coded_data, piece, random_symbol));

    Ok(())
}

此函数使用的输入为

• coding vector：这是你基于 piece_count 随机创建的系数，这将用于创建编码向量。
• coded_data：是一个空数组，在完成编码函数后，此变量将具有数据。

这是从外部调用此函数的方式：

pub fn code_with_buf<R: Rng + ?Sized>(&self, rng: &mut R, full_coded_piece: &mut [u8]) -> Result<(), RLNCError> {
    if full_coded_piece.len() != self.get_full_coded_piece_byte_len() {
        return Err(RLNCError::InvalidOutputBuffer);
    }

    let (coding_vector, mut coded_data) = full_coded_piece.split_at_mut(self.piece_count);

    rng.fill_bytes(coding_vector);
    self.code_with_coding_vector(&coding_vector, &mut coded_data)
}

pub fn code<R: Rng + ?Sized>(&self, rng: &mut R) -> Vec<u8> {
    let mut full_coded_piece = vec![0u8; self.piece_count + self.piece_byte_len];
    unsafe { self.code_with_buf(rng, &mut full_coded_piece).unwrap_unchecked() };

    full_coded_piece
}

让我们解释一下这个函数是如何做的：

self.data
  .chunks_exact(self.piece_byte_len)
  .zip(coding_vector)
  .for_each(
    |(piece, &random_symbol)|
      gf256_mul_vec_by_scalar_then_add_into_vec(coded_data, piece, random_symbol));

此循环是实际创建编码块的位置。

• self.data.chunks_exact(self.piece_byte_len) 将原始数据分成固定大小的块。
• .zip(coding_vector) 将每个块与来自编码向量的相应随机系数配对。
• 对于每个 (piece, random_symbol) 对，我们调用 gf256_mul_vec_by_scalar_then_add_into_vec，它将块乘以 GF(256) 中的系数，并将结果添加到输出缓冲区 coded_data 中。

处理完所有块后，输出缓冲区将保存由编码向量定义的 所有原始块的线性组合。

这里，不是使用普通的整数数学，而是使用 XOR（无进位）进行加法，并以 8 次 不可约多项式 为模进行乘法。所有这些操作都包装在函数内部，因此开发人员可以将它们视为“字段算术”。这就是 Galois Field (GF(256)) 中的计算工作方式。

这里代码使用 GF256，其中每个值、操作都将在范围 (0..255) 内产生结果。

Galois Field: https://en.wikipedia.org/wiki/Finite_field_arithmetic

=> 为了更容易理解，只需相信它是一种类型，它也具有像我们的普通整数数学一样的乘法、加法、除法、减法。

解码器：

这部分比较棘手——它肯定会让你想起你的代数课，因为解码 RLNC 基本上就是解线性方程组。

首先，记住我们之前看到的求解线性方程的小例子吗？嗯，计算机不能像我们在纸上那样“弄清楚”。我们实际上需要 实现一个算法 来求解这些方程。这里使用的标准方法是 高斯消元法。

高斯消元法是一种求解线性方程组的算法。思路是应用 行运算（交换、乘法、加法）将矩阵转换为 行阶梯形 (REF) — 三角形“阶梯”形式。一旦进入 REF，我们就可以通过 反向替换 求解系统。

我将以 RREF (Reduced Row Echelon Form) 为例进行解释：

让我们采用简单的等式：

2x + 3y = 8
x - y   = 1

步骤 1： 执行一些操作以获得我们的第一个 REF。

交换两行 R1 和 R2：

[ 1  -1 |  1 ]
[ 2   3 |  8 ]

通过 R2 = R2 – 2*R1 消除第二个方程中的“2”。

[ 1  -1 |  1 ]
[ 0   5 |  6 ]

从这里开始，在第二行：5y = 6 是一个 REF。使用 反向替换，你将得到 y = 6/5。

步骤 2： 执行一些操作以获得我们的第二个 REF。=> 我们最终得到 RREF 形式。

规范化第 2 行（除以 5）：

[ 1  -1 |  1   ]
[ 0   1 |  1.2 ]

消除上面“-1”：R1 = R1 + R2

[ 1   0 |  2.2 ]
[ 0   1 |  1.2 ]

👉 这是 RREF。现在我们可以直接读取解决方案：

x = 2.2
y = 1.2

该代码将实现整个过程：

Decoder 结构体：

##[derive(Clone, Debug)]
pub struct Decoder {
  /// Stores the coefficient matrix and coded data rows concatenated.
  /// Each row is a coded piece: `[coding_vector | coded_vector]`.
  matrix: DecoderMatrix,
  /// The byte length of each original data piece.
  piece_byte_len: usize,
  /// The minimum number of useful coded pieces required to decode.
  required_piece_count: usize,
  /// The total number of coded pieces received so far.
  received_piece_count: usize,
  /// The number of linearly independent pieces received so far.
  useful_piece_count: usize,
}

初始化函数：

pub fn new(piece_byte_len: usize, required_piece_count: usize) -> Result<Decoder, RLNCError> {
  if piece_byte_len == 0 {
      return Err(RLNCError::PieceLengthZero);
  }
  if required_piece_count == 0 {
      return Err(RLNCError::PieceCountZero);
  }

  Ok(Decoder {
      matrix: DecoderMatrix::new(required_piece_count, piece_byte_len),
      piece_byte_len,
      required_piece_count,
      received_piece_count: 0,
      useful_piece_count: 0,
  })
}

解码函数：

pub fn decode(&mut self, full_coded_piece: &[u8]) -> Result<(), RLNCError> {
    if self.is_already_decoded() {
        return Err(RLNCError::ReceivedAllPieces);
    }
    if full_coded_piece.len() != self.get_full_coded_piece_byte_len() {
        return Err(RLNCError::InvalidPieceLength);
    }

    let rank_before = self.matrix.rank();

    unsafe { self.matrix.add_row(full_coded_piece).unwrap_unchecked().rref() };
    self.received_piece_count += 1;

    let rank_after = self.matrix.rank();

    // If the rank didn't increase, the piece was not useful.
    if rank_before == rank_after {
        Err(RLNCError::PieceNotUseful)
    } else {
        self.useful_piece_count = rank_after;
        Ok(())
    }
}

add_row 函数将使用高斯消元法执行所有操作。根据添加新行之前和之后矩阵的秩。我们可以知道该行是否与我们的 编码块 线性相关。

结论

在以上章节中，我向你解释了 RLNC 的所有概念，并提供了示例和编码演练。希望你能理解它！

我没有演练代码的一个过程是 重新编码过程，它非常简单，所以我将其留给你处理。

对于 RLNC 库，你可以参考：https://github.com/itzmeanjan/rlnc。

该代码由一位在密码学方面非常强大的人实现，如果你喜欢，请给他一个 star 以支持！

如果你觉得这篇博客不错，请在我的 github 存储库上关注我：https://github.com/perfogic

• 原文链接： blog.blockmagnates.com/i...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～