Pendle Boros AMM 机制

AMM Overview

Boros AMM 用于两种 token 之间的交换，具体来说，是 Boros 中底层资产 funding rate 的 Fix stream token 和 Float stream token 的交换。

一个关键挑战是 token 价值的时间敏感性（随着floating stream的缩短而减少）。为了解决这个问题，Boros 使用了一种包含时间加权因子的 constant product（ xy = k）恒定乘积公式的变体。

Technical Architecture

Tokenization of interest stream

• Float stream token
  • Float stream token 的价值定义为从现在至到期期间 1 单位资产，按照当前 funding rate 计算的收益

 float stream token = floating rate from now to maturity × (time until maturity in years)

• 示例：ETH boros 市场当距离到期还有 3 个月，且 float funding rate 为 10% 时，1 个 float stream token 的价值为 0.025 notional(ETH)。
  • Fixed stream token
• Fix stream token 的价值 定义为从现在到到期期间 1 单位资产，按照 fix funding rate 计算的收益

 fix stream token = (1 notional) × time until maturity in years

除了 AMM 通过在 Boros 中开立 long rate position 持有的总 float stream token 外，还使用了一定数量的"virtual float stream token"。

• Tradable liquidity 定义为两者价值的总和：

​​​​tradable liquidity = float stream tokens (valued by market rate)
​​​​+ virtual float stream tokens (valued by market rate)
​​​​+ fix stream tokens (in notional)

Time Definitions and AMM Operation

• T 距离到期的时间，以年为单位。
• t (归一化) 距离到期的时间， 1 即开始， 0 即到期， contract 中通常被称为 timeRatio。
• t = T / total duration

AMM 包含一个 buffer ( B) 以防止清算，AMM 中收取的 fix stream token 和 float stream token 的手续费会进入 buffer。并且，AMM 中持有的 float stream token 会持续产生 funding fee 收益，也会进入 buffer，因此随着时间推移，buffer 中的资金会越来越多，资产也更安全。

Notation

• x 是 AMM 中持有的 float stream token 数量。
• a 是 AMM 中虚拟流动性数量。
• y 是 AMM 中持有的 fix stream token 数量。
• B 是 AMM 中的 buffer。
• totalFloatAmount：在 contract 中表示 (x+a)
• normFixedAmount：在 contract 中表示 (y*t)，代表 AMM 拥有的 fix stream tokens 的数量 * 时间因子

这些数量不受时间因子 t 的影响。

Core Mechanism

AMM 使用 "shifted constant product formula" (恒定乘积公式的平移变体)，公式为：

$$ (x+a)^t ∗ yt = k $$

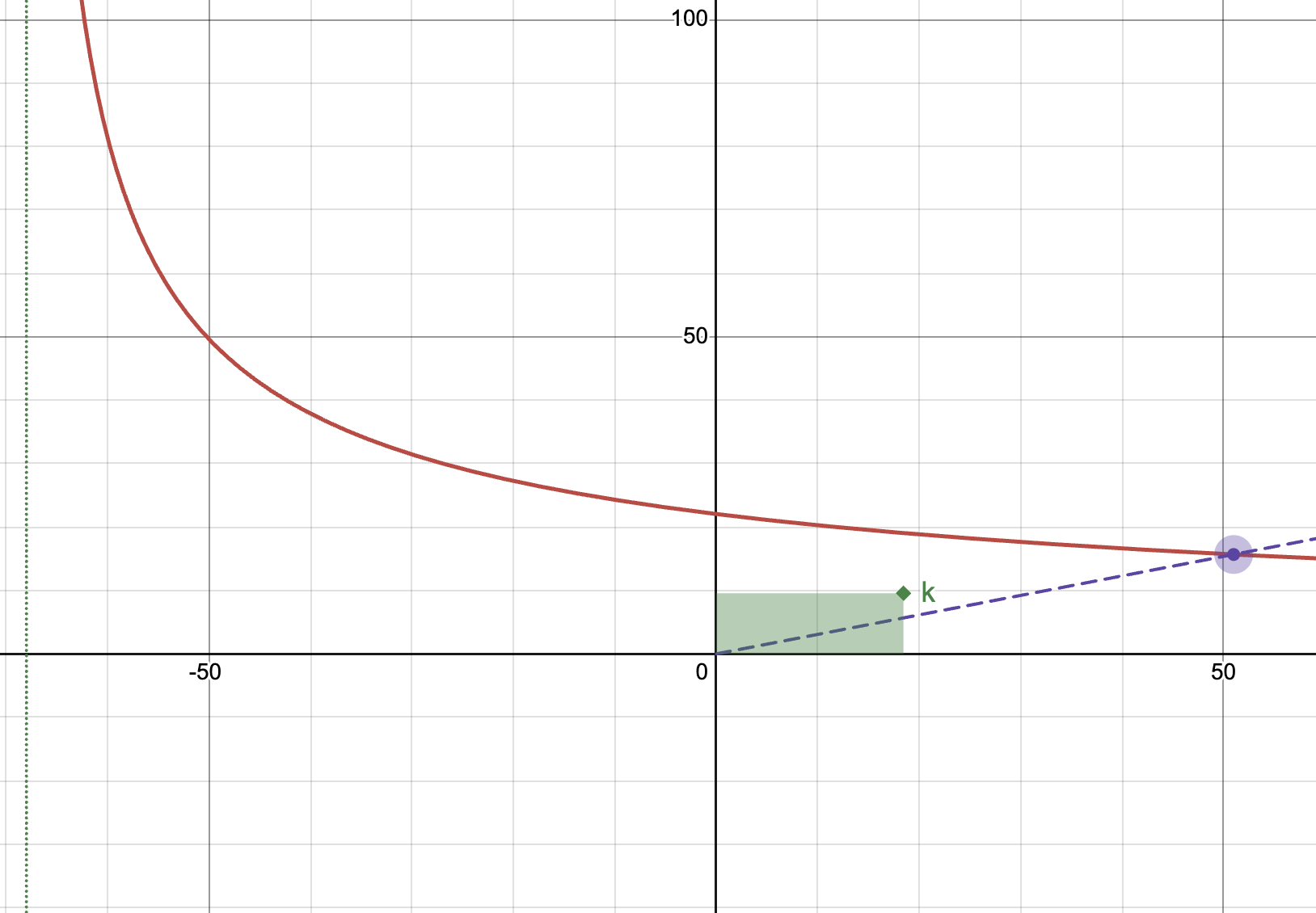
红色曲线为AMM公式，紫色虚线代表当前 Implied APR (AMM price), 绿色区域代表流动性 k

t 的目的是确保没有发生 swap 时，pool 的 implied APR 不随时间变化。

Spot price formula (AMM 价格公式)：

$$ 1 floatstreamtoken= \frac {y∗t} {x+a} fixstreamtoken $$

这意味着 AMM 的 implied APR (隐含年利率) 为：

$$ \frac yt {x+a} ∗ 100% $$

Note: 注意 spot price 公式分母中不包含指数 t。 spot price 等价于 implied APR。

在同一个时间点（固定 t），完全可以将这个公式等价于平移之后的 constant product 公式，其特性和 uniswap V2 一致。

而当 t 变化时，假设没有发生 swap，或者 add/remove liquidity，那么为了保证兑换比例 implied APR 不变，x 和 y 的值会发生变化。所以随着时间推移：

• t 会逐渐变小(从 1 到 0)
• yt 保持不变， (x+a)t 保持不变
• 则 x 会逐渐变大， y 会逐渐变大
• 曲线会随时间上移，曲度变小

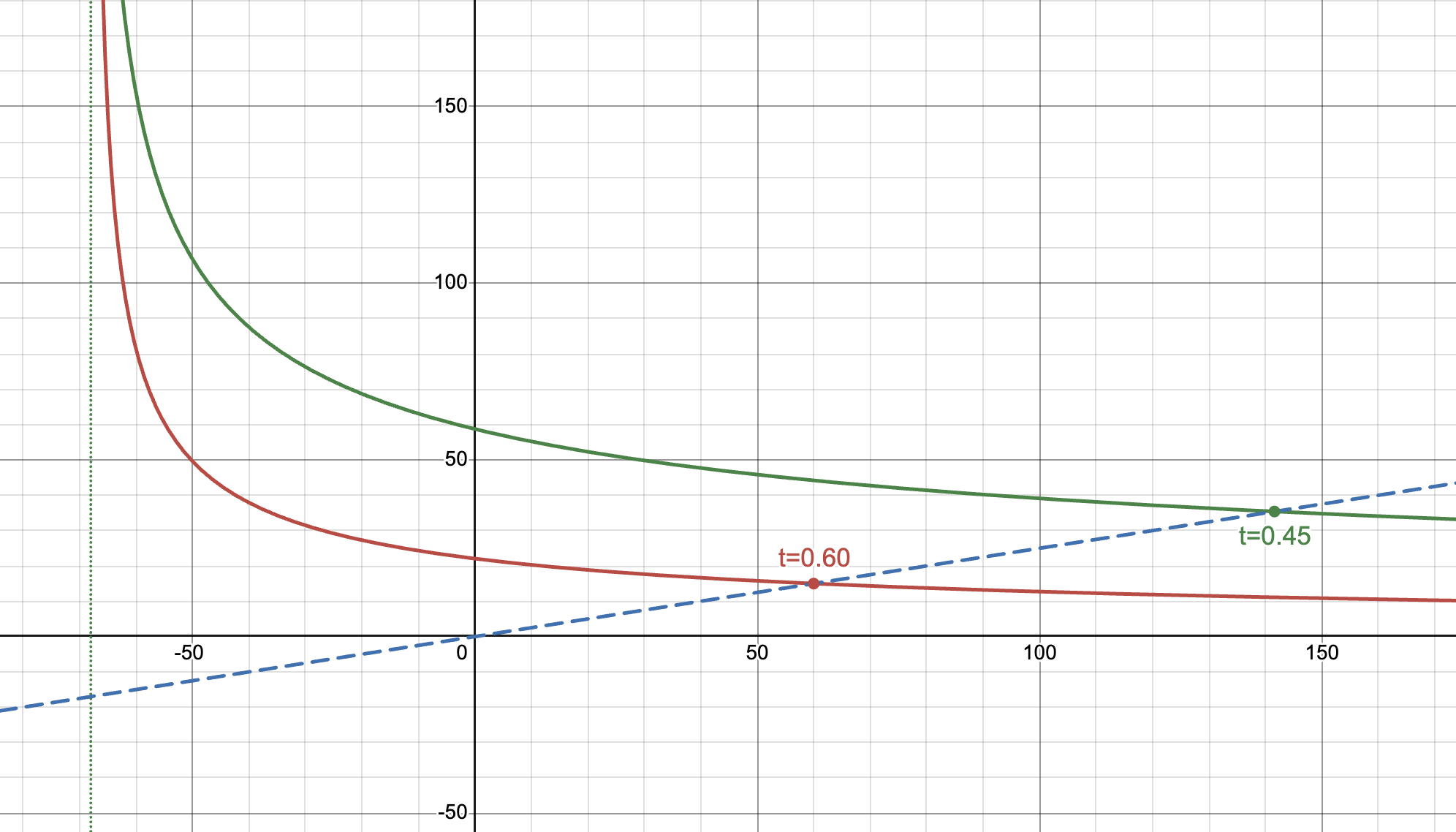
兑换比例 implied APR 不变的情况下，代表价格的蓝色虚线与曲线的交点会随时间向右上方移动，x 和 y 也会增大

Boros AMM Formula Desmos

Seeding

在 seeding time (t = 1， 即市场开始时)，必须为 AMM 提供以下参数：

• Quantity of floating stream tokens (x)：决定 AMM 对市场的初始风险敞口
• Quantity of virtual floating stream tokens (a)：允许 x 低于 0（即 short rate position），即开空 funding rate。a 本质上是 AMM 可以开空 funding rate 的上限。
• Market rate r：例如，r = 0.10 表示 10% 的 market rate。这个参数决定了 AMM 初始的 implied APR

Seeding's Collateral and LP Tokens

Collateral C：是 fix stream tokens + buffer。

• 所需 fix stream tokens 数量可使用公式计算： $ y=(x+a)r $
• 总抵押资产 collateral 要求：$ C≥yT $
• 初始 buffer B 定义为 excess portion： $ B=C−yT $
• 为 seeder（初始流动性提供者）释放 LP tokens，公式：$L=√(x+a)y$ （此时 t=1 公式简化）

seeding steps：

1. 确定初始 AMM pool 的参数 (x,a,r,C)。检查是否 $C≥(x+a)rT$
2. 以 Market rate r 计算 AMM 的 $(x+a), yt, k 等参数。
3. 为 AMM 提供 C notional 作为抵押资产

Swap

$$ (x+a)^t yt=k′ $$

其中 k' 在特定时间 t 是常数（只考虑 swap，没有流动性变化）。

假设用户 u 想在时间 t2 购买 Δx float stream tokens（即 long rate）。AMM 的当前状态是

$(x_1+a , y_1t_1)$，最后更新时间是 $t_1$。

Note: 在持续时间 $t_1$ 到 $t_2$ 期间， fix stream tokens 的数量从 $y_1$ 增加到 $y_1^′$，使得 $y_1^′t_2=y_1t_1$（t 随时间变小，y 随时间变大）。

AMM的状态使用以下公式更新：

• swap 之前，计算当前 k 值， $k_2^′=(x_1+a)^{t2}×(y_1^′t_2)$
• 由于 $y_1^′t_2=y_1t_1$，所以 $k_2′=(x_1+a)^{t2} ×(y_1t_1)$
• $x_2 = x_1 −Δx $
• $y_2t_2 = \frac {k_2^′} { (x2+a)t_2} $
• $Δy = \frac {y_1^′ t_2 − y_2 t_2} {t_2}$

新状态是 $(x_2+a,y_2t_2)$。

要求：

$new spot price= \frac {y_2t_2} {x_2+a} ≥ m_r$

f定义为 AMM 的 swapping fee。

用户 u 获得 Δy fix stream tokens，相当于 Δy × T notional，并支付

f× |Δx | fix stream tokens = f × Δx × T notional 作为 trading fee，这些费用进入 buffer。

在实践中，用户和 AMM 开立 size 为

Δx 的新 swap（如果 Δx > 0，用户 longs rate，否则 shorts rate），rate 为 Δy / Δx 并支付 swap fee。

Add liquidity

LP tokens 的总数为 L，用户 u 想要 mint d * L 个新的 LP tokens。为此，用户必须添加 d(B + yT) notional（相当于 d * B 进入 buffer 和 d * y fix stream tokens）; 并开设 d * x float stream tokens 数量的 long YU position。(Lu 表示用户 u 持有的 LP tokens 数量。)

显式的状态变化：

• $ L_u=L_u + d × L$（用户的 LP tokens 增加）
• $L=L×(1+d)$（总 LP tokens 增加）
• $y=y×(1+d) <=> (yt)=(yt)×(1+d)$（y参数和yt乘积按比例增加）
• $a=a×(1+d)<=>(x+a)=(x+a)×(1+d)$（a参数和x+a总和按比例增加） （即 totalFloatAmount 按比例增加）

隐含的状态变化：

• $ x=x×(1+d)$（x参数按比例增加）
• $ B=B×(1+d)$（B参数按比例增加）

Remove liquidity

假设 L 是 LP tokens的总数，用户 u 想要 burn d * L 个 LP tokens 以获得 liquidity。在此操作后，用户收到 d*(B + yT) notional（相当于 d * B buffer 和 d * y fix stream tokens）和 d * x float stream tokens。

显式的状态变化：

• $L_u=L_u−d×L$（用户的 LP tokens 减少）
• $L=L×(1−d)$（总 LP tokens 减少）
• $y=y×(1−d)<=>(yt)=(yt)×(1−d)$（y参数和yt乘积按比例减少）
• $a=a×(1−d)<=>(x+a)=(x+a)×(1−d)$（a参数和x+a总和按比例减少） （即 totalFloatAmount 按比例减少）

隐含的状态变化：

• $x=x×(1−d)$（x参数按比例减少）
• $B=B×(1−d)$（B参数按比例减少）

AMM Contract Implementation

Seeding function (init AMM)

PositiveAMMMath.calcSeedOutput 函数，Seeding 的核心逻辑，根据用户提供的参数计算 AMM 的初始状态。

AMMSeedParams 结构体，包含 AMM 的初始参数:

• minAbsRate：最小绝对利率
• maxAbsRate：最大绝对利率
• cutOffTimestamp：市场结算到期时间
• initialAbsRate：初始绝对利率，即 AMM 的初始兑换率(1 float stream token = ? fix stream token)
• initialSize：初始流动性数量（即 L）
• flipLiquidity：虚拟流动性数量（即 a）
• initialCash：初始抵押资产数量（即 C）

Note: 时间轴： seedTime → latestFTime → cutOffTimestamp → maturity

1. seedTime 是 AMM 的创建时间，也是 AMM 的初始化时间
2. latestFTime 是 AMM 的最新时间，最近一次更新的 block.timestamp
3. cutOffTimestamp 是 AMM 的结算到期时间
4. maturity 是 AMM 的到期时间

// PositiveAMMMath.sol
struct AMMSeedParams {
    uint256 minAbsRate;
    uint256 maxAbsRate;
    uint256 cutOffTimestamp;
    uint256 initialAbsRate;
    int256 initialSize;
    uint256 flipLiquidity;
    uint256 initialCash;
}

根据初始化参数计算 AMM 的初始状态：

• totalFloatAmount = initialSize + flipLiquidity, 即 (x+a)
• initialAbsRate 为初始的兑换率，即 $ \frac y {x+a} $，所以 $y=(x+a)× \frac y {x+a} $
  • 即 normFixedAmount = totalFloatAmount * initialAbsRate
• liquidity 即 L，即 $ \sqrt {(x+a)×yt} $
• fixedValue 代表初始状态，AMM 所需要的最小抵押资产数量，使用 y 再乘以市场持续时间得到
  • 假设当前初始兑换率始终不变，那么抵押资产需要能大于向 fixed stream tokens 支付的利息
  • y * market_duration (year)， 即 normFixedAmount * (maturity - latestFTime) / 365 days

Note: 创建 AMM 时，为 seedTime，此时 t 为 1， 所以计算公式可以简化掉 t 的幂运算。

// PositiveAMMMath.sol
function calcSeedOutput(
    AMMSeedParams memory params,
    uint256 maturity,
    uint256 latestFTime
) internal pure returns (AMMState memory initialState) {
    // （x + a）
    uint256 totalFloatAmount = (params.initialSize + params.flipLiquidity.Int()).Uint();
    // （y）= (x + a) * initialAbsRate = (x + a) * (y / (x + a))
    uint256 normFixedAmount = totalFloatAmount.mulDown(params.initialAbsRate);
    // （L）= √((x + a) * (y * t))
    uint256 liquidity = (totalFloatAmount * normFixedAmount).sqrt();

    // minimum collateral requirement
    // fixedValue = y * market_duration (year)
    uint256 fixedValue = (normFixedAmount * (maturity - latestFTime)) / 365 days;
    require(params.initialCash > fixedValue, Err.AMMInsufficientCashIn());

    initialState = AMMState({
        totalFloatAmount: totalFloatAmount,
        normFixedAmount: normFixedAmount,
        totalLp: liquidity,
        latestFTime: latestFTime,
        maturity: maturity,
        seedTime: latestFTime,
        minAbsRate: params.minAbsRate,
        maxAbsRate: params.maxAbsRate,
        cutOffTimestamp: params.cutOffTimestamp
    });
}

AMMFactory.create 函数，部署 AMM 合约；根据 isPositive 参数，调用 PositiveAMMMath.calcSeedOutput 或 NegativeAMMMath.calcSeedOutput 函数，计算 AMM 的初始状态。

目前 Boros 只部署了 BTC 和 ETH 的 PositiveAMM。

// AMMFactory.sol
function create(
    bool isPositive,
    AMMCreateParams memory createParams,
    AMMSeedParams memory seedParams
) external returns (address newAMM) {
    AMMState memory initialState;

    address market = createParams.market;

    (, , , uint32 maturity, , , uint32 latestFTime) = IMarket(market).descriptor();

    if (isPositive) {
        initialState = PositiveAMMMath.calcSeedOutput(seedParams, maturity, latestFTime);
        newAMM = _deployPositiveAMM(createParams, initialState);
    } else {
        initialState = NegativeAMMMath.calcSeedOutput(seedParams, maturity, latestFTime);
        newAMM = _deployNegativeAMM(createParams, initialState);
    }

    emit AMMCreated(newAMM, isPositive, createParams, seedParams);
}

ETH AMM 相关 Seed 参数：

• ammId: 30
• name: "Boros AMM - Binance ETHUSDT 26 Sep 2025"
• seedTime: 1753747200 (2025-07-24 00:00:00)
• initialAbsRate: 75000000000000000 (7.5%)
• initialSize: 51000000000000000000 (51)
• flipLiquidity: 68000000000000000000 (68)
• initialCash: 2000000000000000000 (2)
• minAbsRate: 20000000000000000 (2%)
• maxAbsRate: 500000000000000000 (50%)
• cutOffTimestamp: 1758585600 (2025-09-20 00:00:00)
• oracleImpliedRateWindow: 60 (60 blocks)
• feeRate: 0 (0%)
• totalSupplyCap: 480000000000000000000

Swap function

• Router 调用 swapByBorosRouter 函数
  • 传入 sizeOut 参数，表示用户想要购买的 float stream tokens 数量，即 sizeOut 为正数时，用户 longs rate，为负数时，用户 shorts rate
  • 调用 _applyFee 函数，计算 costOut 和 fee
  • 调用 _swap 函数，计算 costOut 和 fee
  • 返回 costOut 参数，表示用户需要支付的 fix stream tokens 数量（包含手续费）

// BaseAMM.sol
function swapByBorosRouter(
    int256 sizeOut
) external onlyRouterWithOracleUpdate notWithdrawOnly returns (int256 costOut) {
    uint256 fee;
    (costOut, fee) = _applyFee(sizeOut, _swap(sizeOut));
    emit Swap(sizeOut, costOut, fee);
}

• _applyFee 函数，根据 feeRate 计算 fee（输出端收费），并累计到 newCost 中

// BaseAMM.sol
function _applyFee(int256 sizeOut, int256 costOut) internal view returns (int256 newCost, uint256 fee) {
    fee = sizeOut.abs().mulUp(_storage.feeRate);
    newCost = costOut + fee.Int();
}

• _swap 函数，读取 AMM 状态，调用 calcSwapOutput 函数计算 costOut，并更新 AMM 状态

// PositiveAMM.sol
function _swap(int256 sizeOut) internal override returns (int256 costOut) {
    AMMState memory state = _readState();
    costOut = state.calcSwapOutput(sizeOut);
    _writeState(state);
}

calcSwapOutput function

calcSwapOutput 函数，Swap 的核心逻辑，根据核心公式计算 fixedIn

normalizedTime 是时间归一化因子 t， t = T / total duration。

uint256 normalizedTime = calcNormalizedTime(state);

floatOut 为正数时，表示用户 longs rate，AMM 转出 float stream tokens，为负数时，表示用户 shorts rate，AMM 转入 float stream tokens。所以当 floatOut 为正数时，需要验证 AMM 是否有足够的 float stream tokens 来满足用户的需求。

Note: 当 totalFloatAmount 为 1 时， totalFloatAmount.pow(normalizedTime) 会返回 1，所以需要验证 totalFloatAmount 是否大于 floatOutAbs + 1。

uint256 floatOutAbs = floatOut.abs();
if (floatOut > 0) {
    // totalFloatAmount.pow(normalizedTime) does not work when totalFloatAmount = 1
    require(state.totalFloatAmount > floatOutAbs + 1, Err.AMMInsufficientLiquidity());
    unchecked {
        newTotalFloatAmount = state.totalFloatAmount - floatOutAbs; // (x+a)
    }
} else {
    newTotalFloatAmount = state.totalFloatAmount + floatOutAbs; // (x+a)
}

Note: liquidity 代表 L， totalFloatAmount 代表 (x + a)， normFixedAmount 代表 (y*t)；在合约层面始终将 (x+a) 和 (y*t) 当作一个整体，即

L=(x+a)t∗yt 等价于 liquidity = totalFloatAmount^t * normFixedAmount。

下列2行代码即使用核心公式计算新的 (y*t)':

$k=(x+a)^t ∗ yt$

$(yt)′ = \frac k {(x+a)^t} $

• 使用最新的 t 计算 liquidity， 此时 (x+a) 和 (y*t) 都未更新
• 使用新的 (x+a) (即 newTotalFloatAmount) 计算新的 (y∗t) (即 newNormFixedAmount)

// totalFloatAmount: (x+a)
// normFixedAmount: y*t
// k = (x+a)^t * yt
// (yt)' = k / (x+a)^t
uint256 liquidity = state.totalFloatAmount.pow(normalizedTime).mulDown(state.normFixedAmount);
uint256 newNormFixedAmount = liquidity.divDown(newTotalFloatAmount.pow(normalizedTime));

$Δyt=(yt)^′−yt$

$Δy= \frac {Δyt} {t}$

最后计算 (y*t) 的差值，再除以 t，即 fixedIn。

int256 normFixedIn = newNormFixedAmount.Int() - state.normFixedAmount.Int();
return normFixedIn.divDown(normalizedTime.Int()); // fixedIn

另外，为了避免极端价格造成 AMM 流动性损失，需要验证 newNormFixedAmount 是否在 minAbsRate 和 maxAbsRate 之间。（以 ETH 市场为例， minAbsRate 为 0.02， maxAbsRate 为 0.5）

// y*t / (x+a) >= minAbsRate
require(
    newNormFixedAmount * PMath.ONE >= state.minAbsRate * newTotalFloatAmount,
    Err.AMMInsufficientLiquidity()
);
// y*t / (x+a) <= maxAbsRate
require(
    newNormFixedAmount * PMath.ONE <= state.maxAbsRate * newTotalFloatAmount,
    Err.AMMInsufficientLiquidity()
);

完整的 calcSwapOutput 函数如下：

// PositiveAMMMath.sol
struct AMMState {
    /// abstract world
    uint256 totalFloatAmount; // (x+a)
    uint256 normFixedAmount; // (y*t)
    /// real world
    uint256 totalLp; // L
    /// market data
    uint256 latestFTime;
    /// immutable variables
    uint256 maturity;
    uint256 seedTime;
    /// config
    uint256 minAbsRate;
    uint256 maxAbsRate;
    uint256 cutOffTimestamp;
}

function calcSwapOutput(AMMState memory state, int256 floatOut) internal pure returns (int256 fixedIn) {
    uint256 normalizedTime = calcNormalizedTime(state);

    uint256 newTotalFloatAmount;
    uint256 floatOutAbs = floatOut.abs();
    if (floatOut > 0) {
        // totalFloatAmount.pow(normalizedTime) does not work when totalFloatAmount = 1
        require(state.totalFloatAmount > floatOutAbs + 1, Err.AMMInsufficientLiquidity());
        unchecked {
            newTotalFloatAmount = state.totalFloatAmount - floatOutAbs;
        }
    } else {
        newTotalFloatAmount = state.totalFloatAmount + floatOutAbs;
    }

    // totalFloatAmount: (x+a)
    // normFixedAmount: y*t
    // L = (x+a)^t * yt
    // (yt)' = L / (x+a)^t
    uint256 liquidity = state.totalFloatAmount.pow(normalizedTime).mulDown(state.normFixedAmount);
    uint256 newNormFixedAmount = liquidity.divDown(newTotalFloatAmount.pow(normalizedTime));
    require(
        newNormFixedAmount * PMath.ONE >= state.minAbsRate * newTotalFloatAmount,
        Err.AMMInsufficientLiquidity()
    );
    require(
        newNormFixedAmount * PMath.ONE <= state.maxAbsRate * newTotalFloatAmount,
        Err.AMMInsufficientLiquidity()
    );
    int256 normFixedIn = newNormFixedAmount.Int() - state.normFixedAmount.Int();

    state.totalFloatAmount = newTotalFloatAmount;
    state.normFixedAmount = newNormFixedAmount;

    return normFixedIn.divDown(normalizedTime.Int());
}

Add liquidity function

添加流动性，会按照比例( d)增加 AMM 的 totalFloatAmount (即 (x+a))、 normFixedAmount (即 (yt)) 和 totalLp (即 L)。

$$ L^′=L×(1+d)$$

$$(x+a)^′=(x+a)×(1+d)$$

$$(yt)^′=(yt)×(1+d)$$

• Router 调用 mintByBorosRouter 函数
  • 传入 totalCash 参数，表示 AMM 中的抵押资产总数量
  • 传入 totalSize 参数，表示 AMM 中的已开设的仓位总数量（所有用户开设的仓位数量之和），正数代表 longs rate，负数代表 shorts rate
  • 传入 maxCashIn 参数，表示用户愿意添加的最大抵押资产数量
  • 传入 exactSizeIn 参数，表示用户想要添加的流动性数量 (即 dL)
  • 调用 _mint 函数，计算 netCashIn 和 netLpOut

Note: 在 mintByBorosRouter 函数中，调用了 2 次 _mint 函数，但参数类型不同，第一次是 PositiveAMM._mint()，第二次是 BOROS20._mint()。

• 检查用户当前的 net cash 是否为正数，负数无法添加流动性
• PositiveAMM._mint() 函数，调用 calcMintOutput 函数，计算 netCashIn 和 netLpOut（即添加流动性所需的抵押资产数量和新增 LP tokens 数量）
• BOROS20._mint() 函数，调用 mint 函数，将 netLpOut 的 LP tokens 分配给用户（类似 ERC20._mint() 函数）

// BaseAMM.sol
function mintByBorosRouter(
    MarketAcc receiver,
    int256 totalCash,
    int256 totalSize,
    int256 maxCashIn,
    int256 exactSizeIn
) external onlyRouterWithOracleUpdate notWithdrawOnly returns (int256 netCashIn, uint256 netLpOut) {
    require(totalCash > 0, Err.AMMNegativeCash()); // disable adding liquidity when net cash is negative

    // PositiveAMM._mint()
    (netCashIn, netLpOut) = _mint(totalCash, totalSize, maxCashIn, exactSizeIn);
    // BOROS20._mint()
    _mint(receiver, netLpOut);
    require(totalSupply() <= _storage.totalSupplyCap, Err.AMMTotalSupplyCapExceeded());
    emit Mint(receiver, netLpOut, netCashIn, exactSizeIn);
}

PositiveAMMMath _mint function

• 读取 AMM 状态
• 获取时间加权的市场利率(oracle rate)
• 调用 calcMintOutput 函数，计算 netCashIn 和 netLpOut
• 更新 AMM 状态

// PositiveAMM.sol
using PositiveAMMMath for AMMState;

function _mint(
    int256 totalCash,
    int256 totalSize,
    int256 maxCashIn,
    int256 exactSizeIn
) internal override returns (int256 netCashIn, uint256 netLpOut) {
    AMMState memory state = _readState();
    // FixedWindowObservationLib.calcCurrentOracleRate()
    int256 markRate = IMarket(MARKET).getMarkRate();
    // PositiveAMMMath.calcMintOutput()
    (netCashIn, netLpOut) = state.calcMintOutput(markRate, totalCash, totalSize, maxCashIn, exactSizeIn);
    _writeState(state);
}

PositiveAMMMath calcMintOutput function

PositiveAMMMath.calcMintOutput 函数，Add liquidity 的核心逻辑，根据用户提供的资产计算 LP tokens 的分配。

• state：AMM 的当前状态
• markRate：市场利率（market oracle rate）
• totalCash：AMM 中的抵押资产总数量
• _totalSize：表示 AMM 中的已开设的仓位总数量（所有用户开设的仓位数量之和），正数代表 longs rate，负数代表 shorts rate
• maxCashIn：用户愿意添加的最大抵押资产数量
• exactSizeIn：用户想要添加的流动性数量（即 dL），正数表示 longs rate，负数表示 shorts rate

// PositiveAMMMath.sol
function calcMintOutput(
    AMMState memory state,
    int256 markRate,
    int256 totalCash,
    int256 _totalSize,
    int256 maxCashIn,
    int256 exactSizeIn
) internal pure returns (int256 netCashIn, uint256 netLpOut)

基础验证和状态检查

• 验证市场是否到期
• 验证总抵押资产为正数
• 将小额仓位（< 1e3）归零，避免精度问题
• 验证 exactSizeIn 符号与 totalSize 符号一致，防止用户添加和 AMM 现有仓位符号相反的流动性

bool isMatured = state.maturity <= state.latestFTime;
require(!isMatured, Err.MarketMatured());

assert(totalCash > 0);

// if totalSize < 1e3, set totalSize to 0
int256 totalSize = _snapSmallSizeTo0(_totalSize);

// This also applies to sign() == 0
require(totalSize.sign() == exactSizeIn.sign(), Err.AMMSignMismatch());

• 当 AMM 没有开设仓位时，LP tokens 直接按比例计算流动性增量，以 maxCashIn 为抵押资产，计算出 netLpOut
• 当 AMM 有开设仓位时
  • isPositionValuePositive：判断 AMM 现有仓位是否和市场利率（market oracle rate）方向一致
  • 根据 isPositionValuePositive 判断 LP tokens 的分配方式（选择对 AMM 更有利的取整方向）
  • true: 使用向下取整除法
  • false: 使用向上取整除法 rawDivUp
  • dL = LP × (期望添加的仓位 / AMM 总仓位)
  • 使用向上取整确保用户有足够的抵押资产 netCashIn
  • 确保计算出的现金需求不超过用户设定的最大值 maxCashIn

if (totalSize == 0) {
    netLpOut = (state.totalLp * maxCashIn.Uint()) / uint256(totalCash);
    netCashIn = maxCashIn;
} else {
    uint256 absTotalSize = totalSize.abs();
    uint256 absExactSizeIn = exactSizeIn.abs();

    bool isPositionValuePositive = totalSize.sign() == markRate.sign();
    if (isPositionValuePositive) {
        // round down
        netLpOut = (state.totalLp * absExactSizeIn) / absTotalSize;
    } else {
        // round up
        netLpOut = (state.totalLp * absExactSizeIn).rawDivUp(absTotalSize);
    }

    netCashIn = (uint256(totalCash) * netLpOut).rawDivUp(state.totalLp).Int();

    require(netCashIn <= maxCashIn, Err.AMMInsufficientCashIn());
}

完整的 calcMintOutput 函数如下：

function calcMintOutput(
    AMMState memory state,
    int256 markRate,
    int256 totalCash,
    int256 _totalSize,
    int256 maxCashIn,
    int256 exactSizeIn
) internal pure returns (int256 netCashIn, uint256 netLpOut) {
    bool isMatured = state.maturity <= state.latestFTime;
    require(!isMatured, Err.MarketMatured());

    assert(totalCash > 0);

    int256 totalSize = _snapSmallSizeTo0(_totalSize);

    // This also applies to sign() == 0
    require(totalSize.sign() == exactSizeIn.sign(), Err.AMMSignMismatch());

    if (totalSize == 0) {
        netLpOut = (state.totalLp * maxCashIn.Uint()) / uint256(totalCash);
        netCashIn = maxCashIn;
    } else {
        uint256 absTotalSize = totalSize.abs();
        uint256 absExactSizeIn = exactSizeIn.abs();

        bool isPositionValuePositive = totalSize.sign() == markRate.sign();
        if (isPositionValuePositive) {
            netLpOut = (state.totalLp * absExactSizeIn) / absTotalSize;
        } else {
            netLpOut = (state.totalLp * absExactSizeIn).rawDivUp(absTotalSize);
        }

        netCashIn = (uint256(totalCash) * netLpOut).rawDivUp(state.totalLp).Int();

        require(netCashIn <= maxCashIn, Err.AMMInsufficientCashIn());
    }

    state.totalFloatAmount += (state.totalFloatAmount * netLpOut) / state.totalLp;
    state.normFixedAmount += (state.normFixedAmount * netLpOut) / state.totalLp;
    state.totalLp += netLpOut;
}

Remove Liquidity

整体上与 Add Liquidity 是反向的逻辑，销毁用户的流动性，返还抵押资产。

settlement

与永续合约机制类似，为了保证 AMM 的价格（ implied APR）与外部市场价格一致，需要定期进行结算（类似 funding fees）。

以 Binance ETHUSDT 市场为例，结算周期为 8 小时（与 funding fees 一致）。假设用户开设了 +10 YU（long rate position），即名义价值 10 ETH 的仓位（并非实际 10 ETH，而是代表 10 ETH 仓位的 funding fees 权益），当结算时，AMM APR 为 7%，而外部市场（binance ETH_USDT_perp）funding rate 为 10.5%，如果按照当前节点结算前一个周期，那么用户将获得：

10 YU * (10.5% - 7%) * 8 hours / 1 year 约等于 0.0003196 YU

Boros 引入了 Index 机制，类似 Aave 的利息索引。合约内部会有 FIndex 用于累计每个区块的 floatingPrice 和 feeRate：

FIndex - 由以下字段组成的结构：

• fTime - 时间戳
• floatingIndex - 对应于 fTime 的支付索引
• feeIndex - 对应于 fTime 的费用索引

FIndexOracle 会周期性触发 updateFloatingIndex 函数，更新 FIndex。

$pFloat(t) = ∑_{i=0} ^{n−1} (floatingIndex(ti+1)−floatingIndex(ti))×s(ti+1)$

$pFees(t)=−∑{i=0} ^{n−1} |s(ti+1) |×Fsettlement(t{i+1})×(t_{i+1}−t_i)$

简单来说，index 机制就是每隔一段时间，累计一次

ΔpFloat∗Δt 和 ΔpFees∗Δt，而结算时方便计算：

• 用户当前开设的仓位 signedSize
• 当前的 FIndex current
• 上一个结算周期的 FIndex last
• 本轮结算 Payment 为 signedSize × (current.floatingIndex - last.floatingIndex)
• 本轮的结算手续费 |signedSize| × (current.feeIndex - last.feeIndex)

// contracts/lib/PaymentLib.sol
library PaymentLib {
    ...

    function calcSettlement(int256 signedSize, FIndex last, FIndex current) internal pure returns (PayFee res) {
        if (last == current) return PLib.ZERO;

        res = PLib.from(
            signedSize.mulFloor(current.floatingIndex() - last.floatingIndex()),
            signedSize.abs().mulUp(current.feeIndex() - last.feeIndex())
        );
    }
}

总结

Boros AMM 通过创新的时间加权恒定乘积公式 (x + a)^t * yt = k，成功解决了 funding rate token 时间敏感性的核心挑战。该机制不仅支持 float stream token 和 fix stream token 之间的高效交换，还通过虚拟流动性、buffer 机制和定期结算确保了系统的稳定性和安全性。

Boros AMM 的核心优势在于：

• 时间感知定价：通过时间因子 t 确保 implied APR 在无交易时保持稳定
• 风险对冲：支持用户对 funding rate 进行多空操作，实现利率风险的对冲
• 流动性管理：通过 LP token 机制和动态调整，为流动性提供者提供合理的收益分配
• 价格发现：通过 AMM 机制实现 funding rate 的市场化定价

Reference

• Boros APP
• Boros Whitepaper
• Boros Contract
• Boros SDK
• Boros Docs

• 本文转载自： hackmd.io/@6wZ99QXPQfWeg... , 如有侵权请联系管理员删除。