Uniswap V3 详解
在Uniswap V3代码库中计算两个价格之间的真实储备量
- RareSkills
- 发布于 2025-10-06 12:51
- 阅读 1132
本文介绍了Uniswap V3代码库中用于计算两个价格之间真实储备量的公式,重点讲解了SqrtPriceMath.sol库中的getAmount0Delta和getAmount1Delta函数,解释了它们如何使用Q64.96格式的价格平方根来计算代币X和Y的储备量,以及在流动性提供和移除过程中如何进行四舍五入。
在 Uniswap V3 代码库中计算两个价格之间的真实储备
在之前的章节中,我们推导了计算一个分段中两个价格之间的 X 和 Y 代币的真实储备的公式。当用户添加或移除流动性,以及在交易期间,协议会使用这些公式。
在本章中,我们将展示这些公式在代码库中的位置。由于协议以 Q64.96 格式存储价格的平方根,因此必须调整公式以使用这种格式。
在代码库中计算数量 x_r 和 y_r
代码库包含用于计算在恒定流动性下,两个价格之间的 X 和 Y 代币数量的辅助函数。这些函数在 SqrtPriceMath.sol 库中定义,名称如下:
getAmount0Delta:计算给定流动性下,两个价格之间的 X 的真实储备。getAmount1Delta:计算给定流动性下,两个价格之间的 Y 的真实储备。
这些真实储备的公式实际上取决于价格的平方根,而不是价格本身。 我们可以通过对该值求平方来从其平方根中恢复价格——但这仅在链下完成; 在链上没有必要。
为简洁起见,我们将继续引用价格,但读者应该知道该协议仅使用价格的平方根。 例如,如果协议需要计算价格 100 和 200 之间的真实储备量,它将使用参数 100 和 200(均为 Q64.96 格式)调用这些函数,而不是 100 和 200。
函数 getAmount0Delta 和 getAmount1Delta
SqrtPriceMath 库有两个名为 getAmount0Delta 的函数,其中一个具有以下签名,另一个将在后面的章节中讨论。
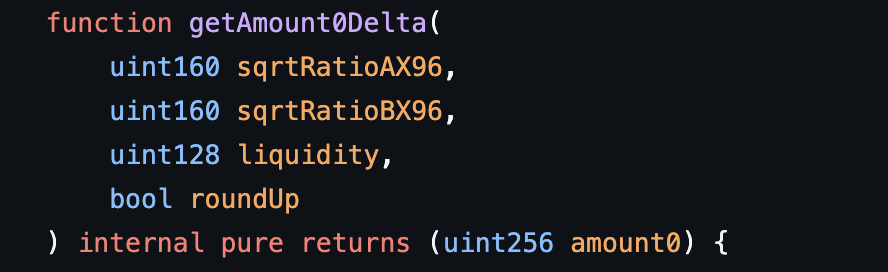
它接收 Q64.96 格式的两个价格的平方根(sqrtRatioAX96 和 sqrtRatioBX96),流动性以及一个布尔值(roundUp),该布尔值指定最终金额应向上还是向下舍入。
当金额代表协议向用户的付款时(例如在交易中或移除流动性时),金额会向下舍入;当金额代表用户向协议的存款时(例如在交易中或提供流动性时),金额会向上舍入。 舍入总是偏向协议,不利于用户。
此函数计算并返回在给定的流动性 L 下,sqrtRatioAX96 和 sqrtRatioBX96 之间代币 X 的真实储备量,假设此分段中的流动性完全是代币 X。
该协议还有两个 getAmount1Delta 函数,其中一个的签名与 getAmount0Delta 非常相似,另一个将在后面的章节中讨论。 它的目的是计算在给定的流动性 L 下,sqrtRatioAX96 和 sqrtRatioBX96 之间代币 Y 的真实储备量,假设此分段中的流动性完全是代币 Y。
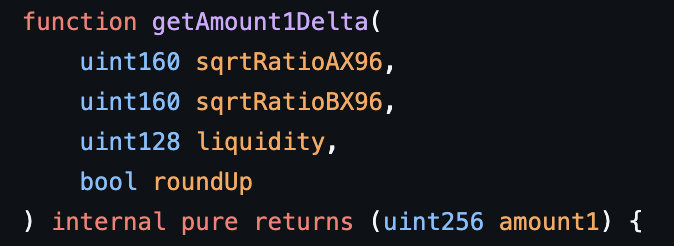
与 getAmount0Delta 相同的舍入行为适用于此函数。
下面的交互式工具可以计算给定流动性的价格区间内的 getAmount0Delta 和 getAmount1Delta 的相同值。 要使用它,请移动蓝色和紫色滑块以调整 sqrtRatioAX96 和 sqrtRatioBX96,并移动橙色滑块以调整流动性。 amount0/amount1 单选按钮指示应执行哪个函数。 要向上舍入结果,请选中 roundUp 复选框。
这里是一个 # Uniswap v3 getAmountDelta 计算器 https://rareskills.io/get-amount-delta-price
请注意,这些函数假定在两个价格点之间,流动性是恒定的,并且仅包含单个储备。
在使用这些函数之前,我们必须事先知道这些信息,因为这些函数不知道流动性在整个可能价格范围内的分布。
函数 getAmount0Delta
函数 getAmount0Delta 计算以下公式,该公式我们在关于真实储备的章节中推导得出:
$$ x_r = \frac{L}{\sqrt{p_a}} - \frac{L}{\sqrt{p_b}} $$
但使用以 Q64.96 格式表示的价格的平方根,由 sqrtRatioAX96 和 sqrtRatioBX96 给出。
由于 $\sqrt{p}$ 和 sqrtRatioX96 之间的关系是
$$\sqrt{p} = \frac{sqrtRatioX96}{2^{96}}$$
我们可以将此关系代入 $x_r$ 的公式,如下所示
$$x_r = \frac{L} {\sqrt p_a} – \frac{L} {\sqrt p_b}$$ $$x_r = \frac{L} {\frac{sqrtRatioAX96}{2^{96}}} – \frac{L} { \frac{sqrtRatioBX96}{2^{96}}}$$ 代入 $\sqrt {p_a}$ 和 $\sqrt {p_b}$ $$x_r = \frac {L \cdot 2^{96}} {sqrtRatioAX96} - \frac {L \cdot 2^{96}} { sqrtRatioBX96}$$ 将 $2^{96} $移到分子 $$x_r = \frac{L \cdot 2^{96} \cdot (sqrtRatioBX96 – sqrtRatioAX96)} {sqrtRatioAX96 \cdot sqrtRatioBX96}$$
找到一个共同的分母
最后一步并非严格来说在数学上是必要的,但在除法会引入舍入误差的代码中,它可以提高精度,因为我们只执行一次除法而不是两次除法。
此公式可以在代码库中的函数注释中找到(没有 $2^{96}$)
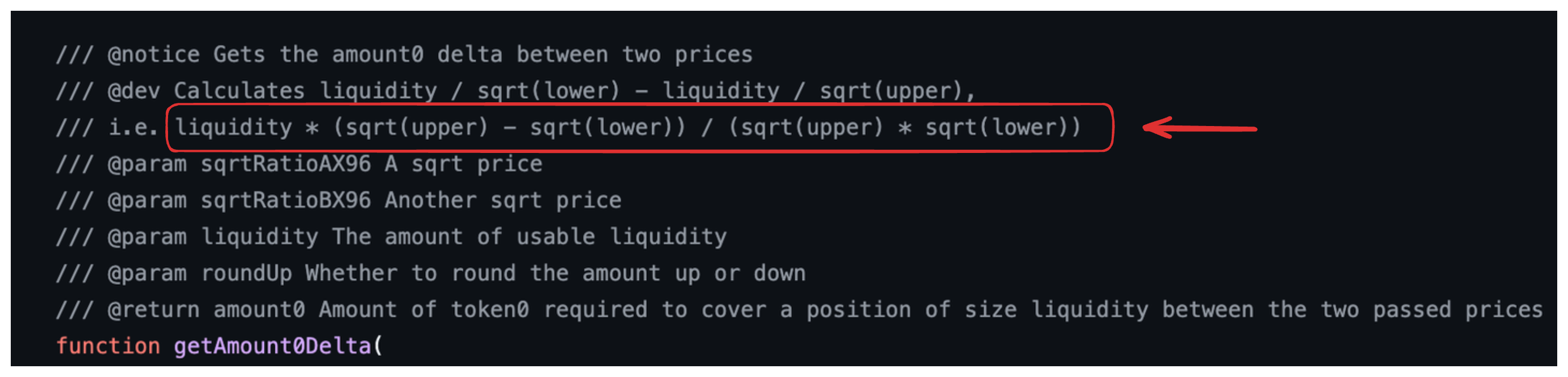
并在函数 getAmount0Delta 中实现:
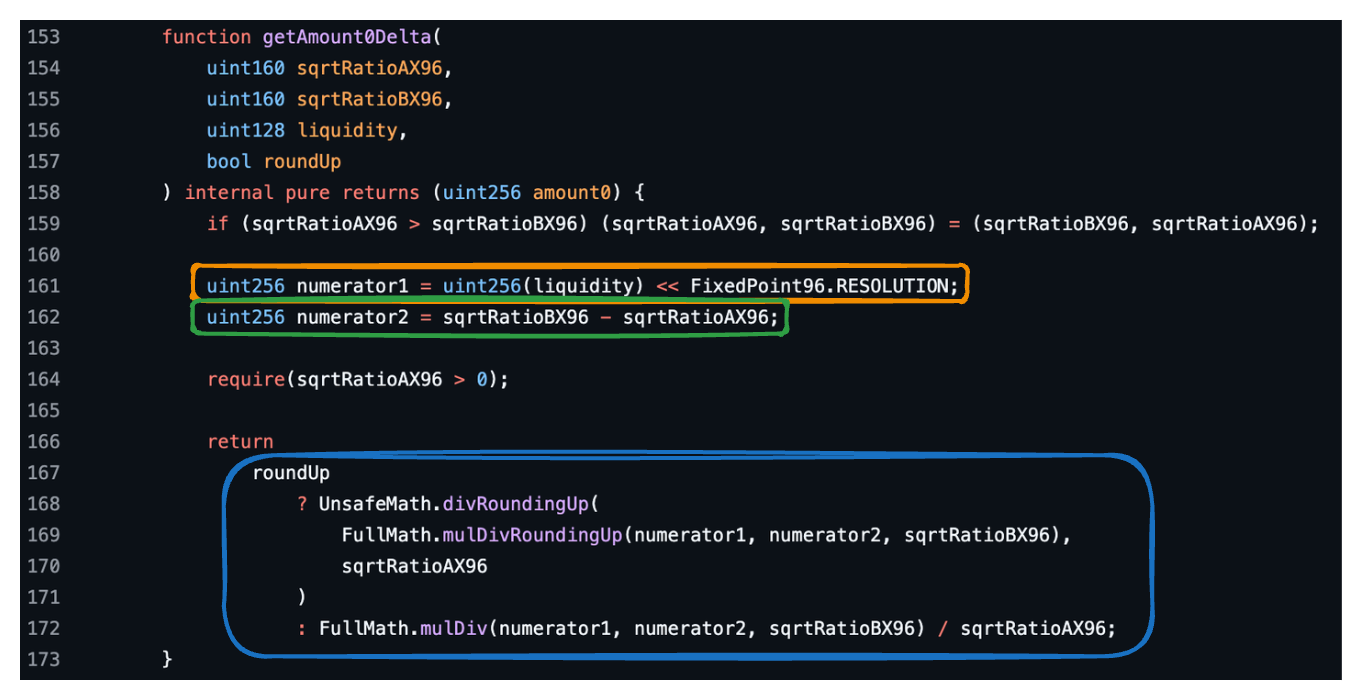
上图中的橙色和绿色框对应于我们刚刚推导出的公式的橙色和绿色部分,它们构成分子。 蓝色框包含完整的表达式,其中分子项乘以并除以 sqrtRatioAX96 和 sqrtRatioBX96。
mulDiv 函数将前两个参数相乘,然后将乘积除以第三个参数。 mulDivRoundingUp 函数执行相同的操作,但向上舍入最终结果。
divRoundingUp 执行向上舍入的整数除法。
如前所述,roundUp 参数指示是否应向上舍入最终金额。
函数 getAmount1Delta
此函数的目标是计算以下公式
$$y_r = L \sqrt p_b – L \sqrt p_a$$
但用 sqrtRatioAX96 和 sqrtRatioBX96 代替 $\sqrt p_a$ 和 $\sqrt p_b$。
请记住,$\sqrt p$ 和 sqrtRatioX96 之间的关系是
$$p = \frac{sqrtRatioX96}{2^{96}}$$
然后我们可以在 $y_r$ 的公式中使用此关系,如下所示
$$y_r = L \sqrt p_b – L \sqrt p_a$$ $$y_r = \frac {L \cdot sqrtRatioBX96} {2^{96}} – \frac { L \cdot sqrtRatioAX96}{2^{96}}$$ $$y_r = \frac{L \cdot (sqrtRatioBX96 - sqrtRatioAX96)}{2^{96}}$$
再次,我们重新排列公式以仅进行一次除法,从而提高精度并匹配在代码库中找到的内容。
下图显示了函数 getAmount1Delta。
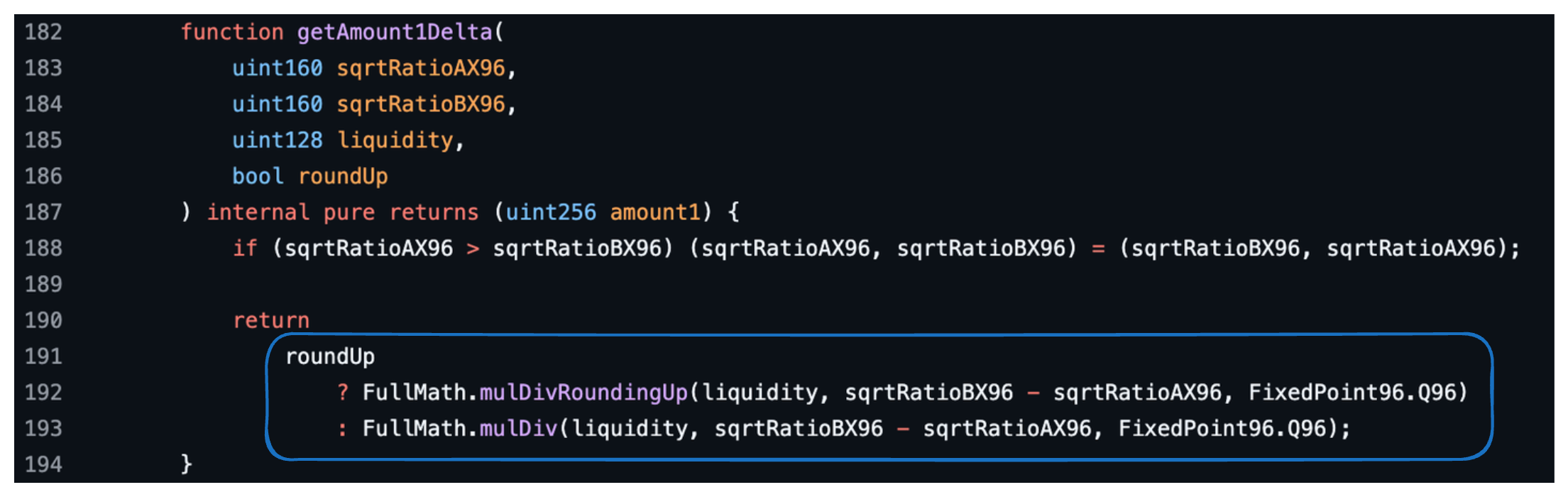
Python 中的函数 getAmount0Delta 和 getAmount1Delta
在本节中,我们将用 Python 编写 getAmount0Delta 和 getAmount1Delta 函数,这些函数将用于计算分段的真实储备。
为简单起见,我们不会担心脚本中的舍入误差。
它们可以写成如下:
import math
def getAmount0Delta(sqrtRatioAX96, sqrtRatioBX96, liquidity, roundUp):
numerator1 = liquidity*2**96
numerator2 = sqrtRatioBX96 - sqrtRatioAX96
if roundUp:
return math.ceil(numerator1*numerator2 / (sqrtRatioBX96*sqrtRatioAX96))
else:
return math.floor(numerator1*numerator2 / (sqrtRatioBX96*sqrtRatioAX96))
def getAmount1Delta(sqrtRatioAX96, sqrtRatioBX96, liquidity, roundUp):
if roundUp:
return math.ceil(liquidity*(sqrtRatioBX96 - sqrtRatioAX96)/2**96)
else:
return math.floor(liquidity*(sqrtRatioBX96 - sqrtRatioAX96)/2**96)假设我们要计算刻度 -10 和 10 之间的真实储备,当前价格正好位于刻度零,如下图所示。 Y 代币的真实储备位于较低刻度 (-10) 和当前价格 (0) 之间,而 X 代币的真实储备位于当前价格 (0) 和较高刻度 (10) 之间。
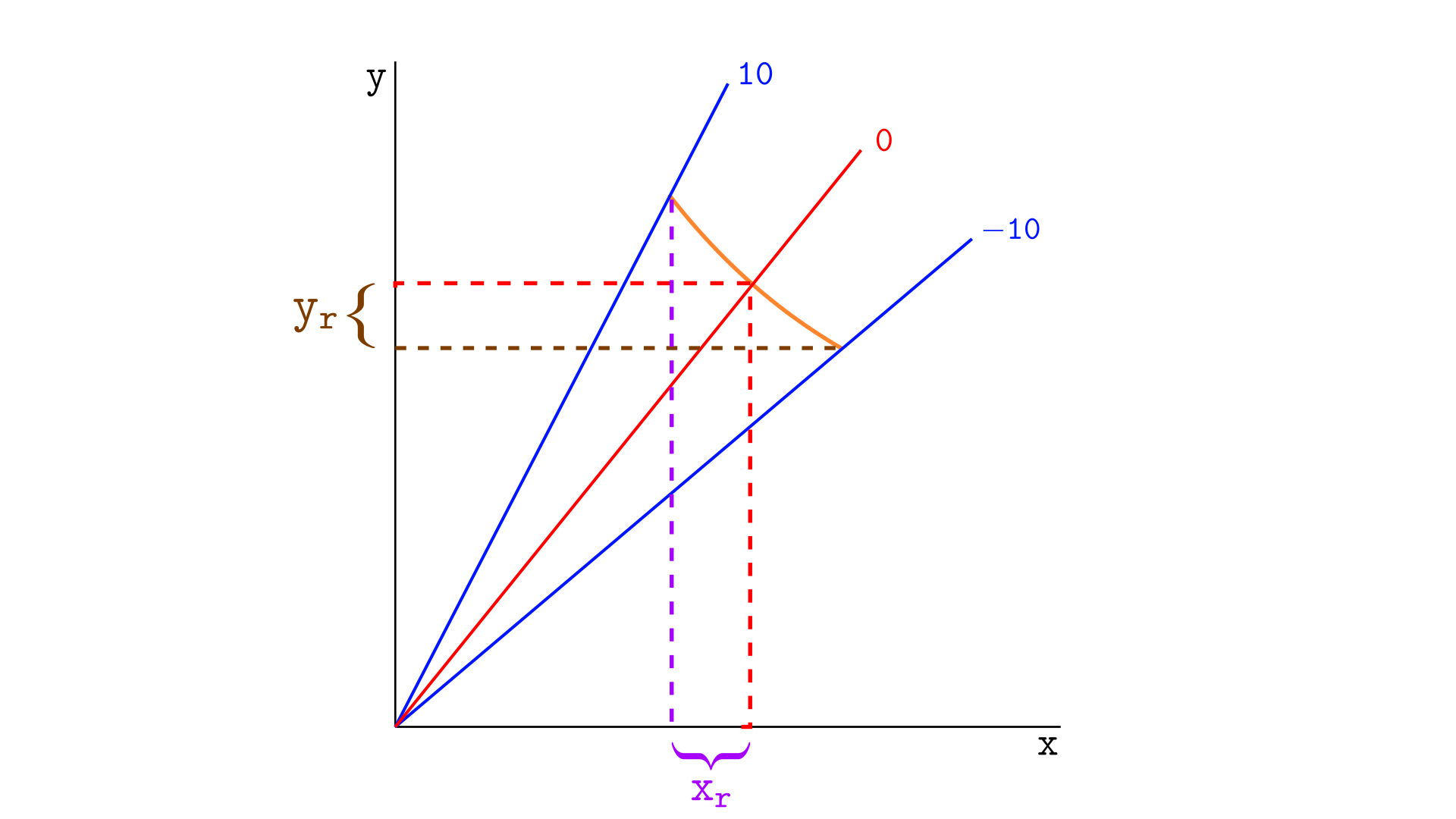
我们可以使用函数 getAmount0Delta 和 getAmount1Delta 来获取这些值。
为了确定是向上还是向下舍入,我们需要考虑计算的目的。 如果计算是用于提供流动性,则结果将向上舍入,反之则用于移除流动性。 让我们在提供流动性时进行这些计算,在这种情况下需要向上舍入。
计算和结果值显示在下面的代码中。
def getSqrtRatioAtTick(i):
return math.sqrt(1.0001 ** i) * 2**96;
current_price = getSqrtRatioAtTick(0)
upper_price = getSqrtRatioAtTick(10)
lower_price = getSqrtRatioAtTick(-10)
print(getAmount0Delta(current_price, upper_price, 1000000000, True)) # 499851
print(getAmount1Delta(lower_price, current_price, 1000000000, True)) # 499851练习:在以下情况下,计算刻度 -10 和 20 之间的真实储备:
- 当前价格位于刻度 -20,
- 当前价格位于刻度 0,
- 当前价格位于刻度 20。
结论
- 该协议提供了计算两个任意价格之间的真实储备的函数,以及它们之间给定的恒定流动性。 这些函数是
getAmount0Delta(对于 X 代币)和getAmount1Delta(对于 Y 代币)。 - 这些函数接收以 Q64.96 格式表示的价格的平方根,变量名为
sqrtRatioAX96和sqrtRatioBX96。 - 如果计算出的真实储备量表示协议将要收到的金额,则向上舍入;如果表示协议将要支付的金额,则向下舍入。
本文是关于 Uniswap V3 系列文章的一部分。
- 原文链接: rareskills.io/post/unisw...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 学分: 16
- 分类: DeFi
- 标签: Uniswap V3 getAmount0Delta getAmount1Delta SqrtPriceMath Q64.96格式 真实储备量
