欺诈证明中 Dispute Games 的实现
- vexil_
- 发布于 2023-07-15 10:49
- 阅读 565
本文介绍了Dispute Games的概念,它是一种通用的争端解决机制,可以用来解决关于信息真实性的争议。文章深入探讨了Bisection Game,这是Dispute Game的一种具体实现,参与者通过不断二分执行轨迹来验证计算的正确性。文章还讨论了Claims、Positions、Chess Clocks以及Bonding等关键概念,并解释了如何在链上执行VM步骤来证明或反驳主张。
争端游戏
过去的一个月对我来说是争端游戏,这是一种非常有趣的机制。这篇文章是我对它们是什么、为什么我认为为通用争端游戏构建基础设施很重要以及我正在实现的函数如何运行的随笔。
感谢 Karl Floersch, protolambda, Joshua (trianglesphere), Mark Tyneway, Inphi, refcell, 和 Adrian Sutton 对下面描述的机制的设计和实现的贡献
Joshua 也将在下周的 EthCC 上发表关于这个主题的演讲!
免责声明:我是 OP Labs 的员工,这些文字仅代表我个人观点。我撰写此帖并不代表 OP Labs 或 Optimism 基金会。此帖子中的所有材料均可能会发生变化,不能作为 OP Stack 将用于支持故障证明的争端游戏的规范。
争端游戏
争端游戏是一种通用机制,它使两个或多个参与方能够解决关于某个信息的声明的争议。我今年早些时候做了一个 演讲,但要将其提炼到本质,通用争端游戏具有两个重要属性:
激励兼容性:为了使游戏具有抗女巫攻击性并鼓励诚实参与者参与,必须对创建错误的声明进行明确的惩罚,并对创建真实的声明进行明确的奖励。
解决:每个争端游戏实现都必须具有一种机制来确定其中提出的声明是 true 还是 false。这可以是多重签名、故障证明或有效性证明,只要它可以确定性地区分游戏中的所有声明为 true 还是 false 在解决时。
在满足这些要求的同时,可以通过多种方式实现争端游戏;因此,我们可以定义一个松散的接口,例如 IDisputeGame 中。此接口定义了最小的功能,例如存储根声明、用于更广泛实现的任意额外数据、用于绑定每个声明的 IBondManager、resolve 函数以及一些其他辅助函数,用于检索有关游戏的数据。
因为可能存在许多不同类型的争端游戏,并且它们通常在依赖于不同的安全模型的同时执行各种特权操作,因此最好有一种方法来创建、记录和升级不同游戏类型的实现。在 Optimism 代码库中,这个想法体现在 DisputeGameFactory 中,它是一个 clones-with-immutable-args 工厂,它将不可变的设置数据传递给最小的游戏代理。能够添加不同的游戏类型并通过工厂验证其操作,这为一些有趣的大门打开了,例如使用多个基于故障证明的游戏创建一个聚合证明系统,这些游戏由不同的程序和 VM(MIPS、RISC-V、WASM 等)保护。
一个简单的、受信任的争端游戏的例子是证明游戏,它保护 Optimism 上的输出根。我们可以想象一个 IDisputeGame 的实现,它添加了一个函数,供受信任的证明者提交 EIP-712 签名,该签名属于提交到替代输出根的类型哈希,并且resolve 函数的实现从 L2OutputOracle 中删除错误的输出根,一旦提交了阈值数量的签名。这个游戏的完整生命周期流程,包括与参与游戏的链下代理的交互,可能如下所示:
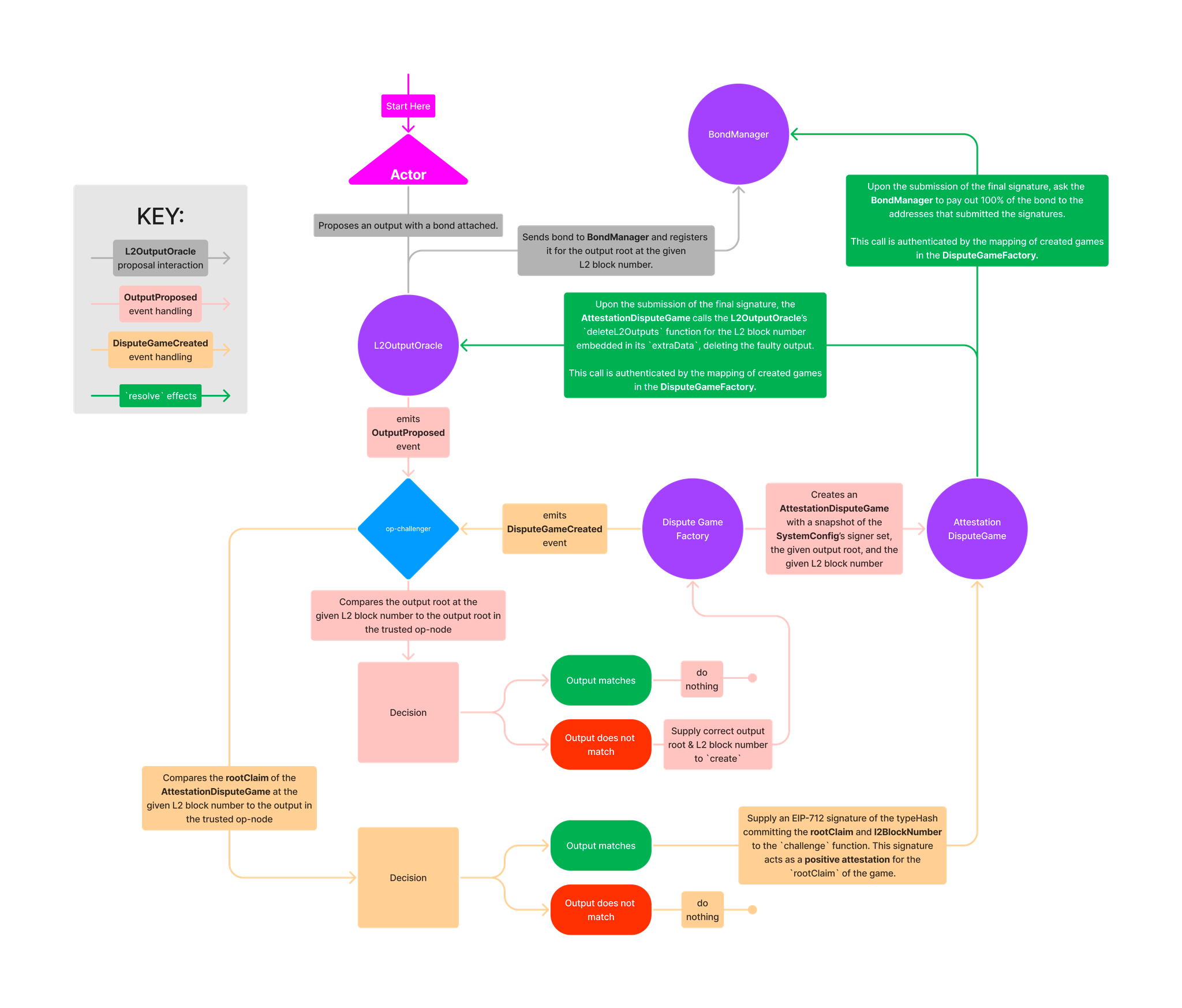
证明游戏图 ALT 但这只是可以构建的众多争端游戏的示例之一,尽管它具有严重缺点,即依赖于证明者集中受信任的各方。
二分游戏
二分游戏是争端游戏的一种特殊实现,其中玩家对执行轨迹进行二分,直到达到单个指令步骤。在这个游戏中,状态转换函数充当游戏的真理来源。为了使这个工作,我们必须有一个约定的prestate, sss,和一个有争议的poststate,s′s's′。状态转换函数,我们从这里开始称之为TTT,可以是任何东西,只要它符合T(s,i)→s′T(s, i) \rightarrow s'T(s,i)→s′的形式,其中sss = 约定的prestate,iii = 状态转换输入,s′s's′ = post state。
游戏的第一个版本实现是为了争论自然数的顺序,所以我们定义TTT为T(s,_)→s+1T(s,\_) \rightarrow s + 1T(s,_)→s+1。在这个游戏中,执行轨迹将由所有自然数组成,按升序排列,从绝对的prestate开始
+ 1。这是一个容易开始的地方,因为在实现更重的状态转换函数之前,游戏可以完全围绕这个状态转换函数构建。而且它有效!
很快,我们将把目光投向集成 MIPS.sol VM,以利用其 step 函数作为状态转换函数。简而言之,MIPS.sol 合约是一个单一的 MIPS 线程上下文,它通过 Linux 系统调用的子集的最小实现来增强,以进行 env 访问。有了这个,我们将能够对 Cannon 和 op-program 生成的轨迹提出异议,从而使用户能够以无需信任的方式挑战 OP Stack 链的输出提案!这是朝着 OP Stack 去中心化迈出的重要一步。在我们深入研究将 MIPS VM 与二分游戏集成的细节之前,这可能值得单独写一篇文章,让我们先介绍一下二分游戏如何使用通用状态转换函数运行。
声明(Claims)
二分游戏中的声明是对 VM 在声明的位置的轨迹索引处的状态的简单承诺。在解决之前,声明没有绝对真理的概念,只有相对于其观察者和创建者的相对真理(薛定谔的声明;盒子里有什么?)。解决完成后,声明会向所有参与者显示为 true 或是 false 。将它们视为 Rust 的 Future 特征的实现,该特征在创建时被等待并在游戏解决阶段完成后解析为 bool 。 未反驳的声明在其对手的国际象棋时钟耗尽后,会隐式地解析为 true ,而被反驳的声明必须依靠指令步骤来解决。
位置
游戏中的每个声明都存在于二叉树中的一个位置,表示该声明所承诺的轨迹指令。位置表示为广义索引,它等于2d+i2^d + i2d+i。广义索引由 Vitalik Buterin 在 eth2 SSZ 规范 中引入。
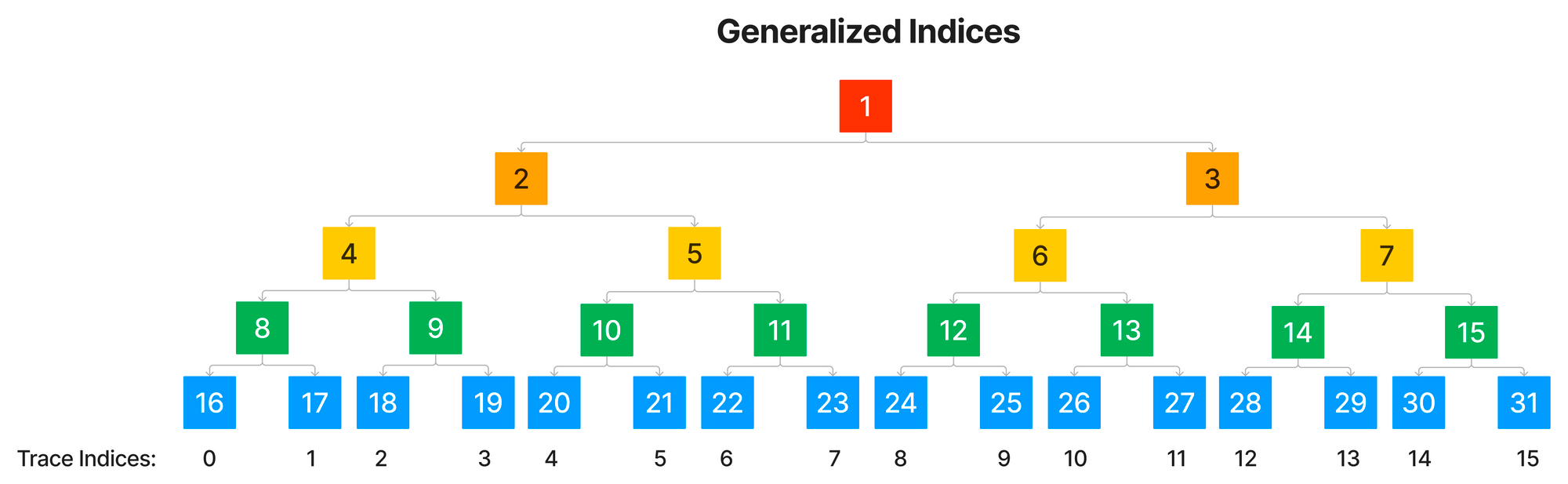
重要的是要区分游戏状态和位置树。游戏状态中的所有声明都存在于树中的一个位置,但同一位置可能存在多个声明,这将在以下各节中进行说明。因此,游戏状态往往看起来更像一个 DAG,其中的子节点始终指向其父节点,并终止于根声明。
所有位置也可以转换为轨迹索引,轨迹索引是声明所承诺的轨迹中指令的索引。可以通过一直向右运行直到达到叶节点,然后从节点的广义索引中拉出iii(取消设置其最高有效位)来找到位置的轨迹索引。

国际象棋时钟

为了使游戏在恒定的时间窗口内可用于解决,我们需要能够对防御者和挑战者的移动进行时间限制。此外,该游戏的核心要求是允许在任何时候免许可地参与任何游戏。这是因为仅限于两个参与者的游戏容易出现恶意制造的僵局或错误地解决。
创建游戏时,会为其提供根声明。根声明承诺整个状态转换,我们可以通过将其位置转换为轨迹索引来看到这一点。创建后,根声明的创建者立即点击他们的国际象棋时钟,开始倒计时以寻找潜在的挑战者。
二分游戏中的国际象棋时钟的功能与传统的完全相同 - 当一个玩家移动时,对手的国际象棋时钟开始tick作响,而他们的时钟暂停。每方开始游戏时,他们的时钟上有 3.5 天,以确保所有移动将在 7 天内耗尽。
因为游戏是免许可的,所以在通往叶节点的路径上可能存在分叉。为了支持这一点,除了根声明和对根声明的初始攻击之外,每个声明都从其祖父母那里继承其时钟持续时间。这是因为声明总是不同意其父母,这也使它们具有与其祖父母一致
移动(Moves)
为了证明一项声明不正确,玩家必须二分到承诺在单个指令步之后 VM 状态的声明。一旦达到这一点,玩家就可以在链上执行单个指令步,这可以证明或反驳一组声明。

进一步二分的移动被称为攻击或防御。因为声明的轨迹索引是有序的,所以如果不同意父声明,我们可以移动到父声明承诺的轨迹范围的中点,或者如果同意父声明但深度不正确,则可以移动到父声明的右侧同级承诺的轨迹范围的中点。如果我们同意父母但不同意祖父母,则我们什么也不做,因为父母是我们本来会提出的声明(如果它不存在)。
如果玩家需要在其自身轨迹范围之外的位置进行移动,则他们只需提出承诺其整个轨迹的声明即可。这样就无需在不同的游戏和不同大小的轨迹中更改树的深度。
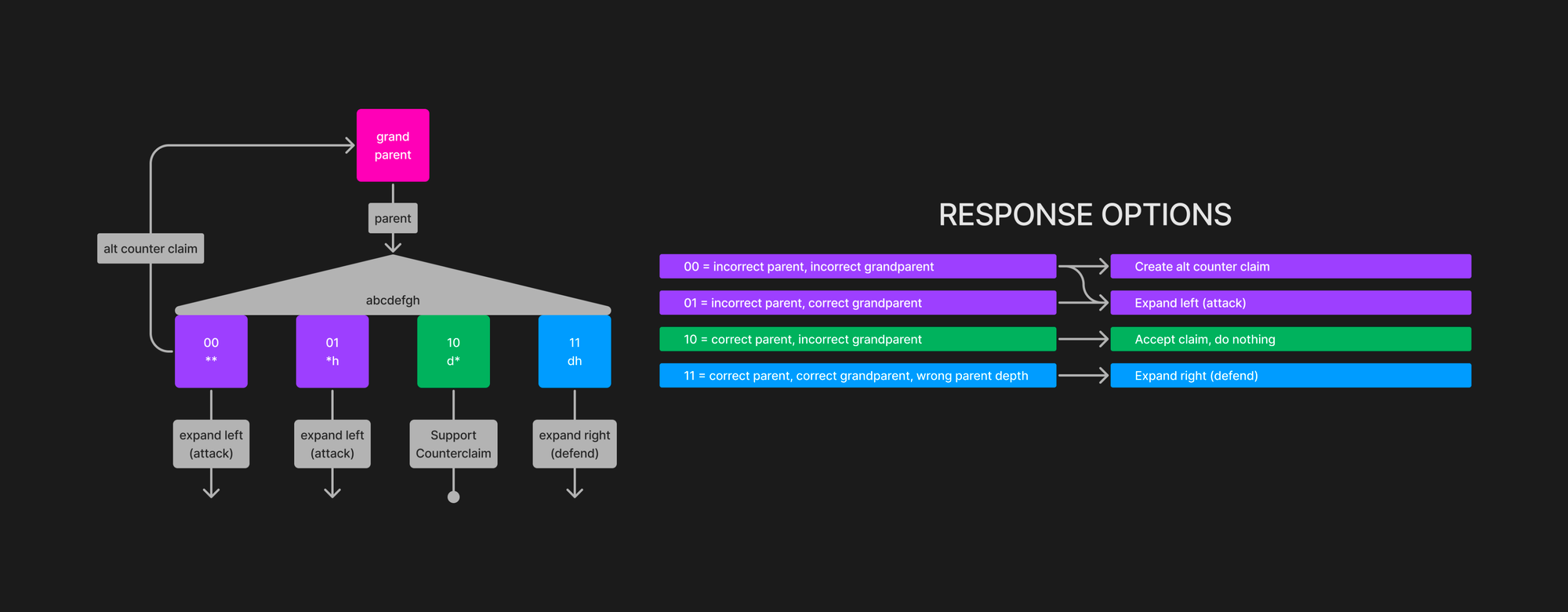
当上述逻辑返回防御响应时,玩家将需要参考其对根声明的看法来确定防御是否为有效的移动。
根声明不正确,并且想要删除玩家同意的输出。
父声明的深度为偶数 - 该移动仍然有效,因为尽管它同意父声明,但玩家本身不会提出此声明,因为它反对根声明。
父声明的深度为奇数 - 该移动无效,因为它支持玩家反对的根声明。玩家不做任何事情。
根声明是正确的,并且想要删除玩家不同意的输出。
父声明的深度为偶数 - 该移动无效,因为它支持玩家反对的根声明。玩家不做任何事情。
父声明的深度为奇数 - 该移动仍然有效,因为尽管它同意父声明,但玩家本身不会提出此声明,因为它反对根声明。
攻击
攻击类似于相对于被攻击的声明遍历到左子位置。这使我们到达一个位置,该位置承诺父位置所承诺的轨迹的一半。
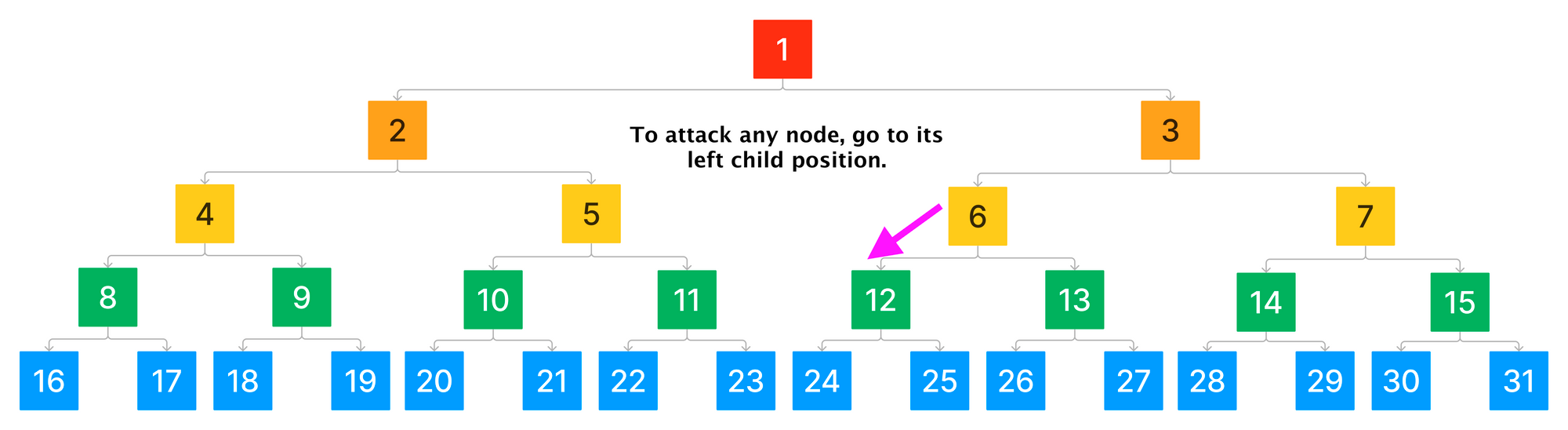
防御
防御类似于遍历到被防御声明的右侧同级的左子节点。这使我们到达一个位置,该位置承诺父节点的右侧同级轨迹的一半。
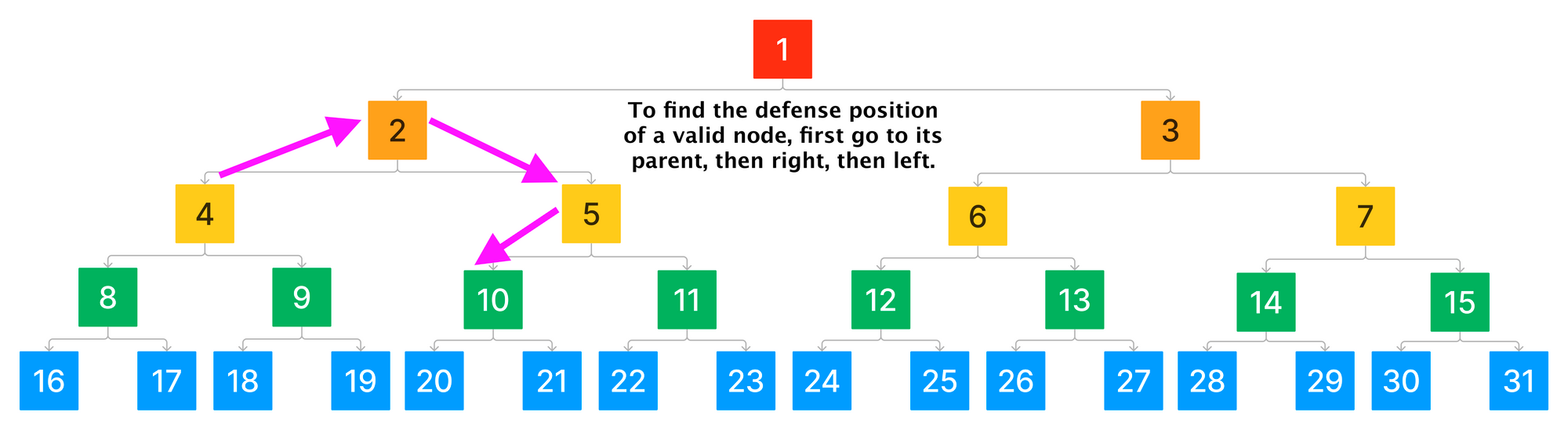
你可能会注意到,由于这两个移动的定义,某些位置可能永远不会在二叉树中遍历到。这些位置在树中具有互补的、有效的、具有相同轨迹索引的位置。我们可以验证所有轨迹索引在游戏内是否具有有效的移动:
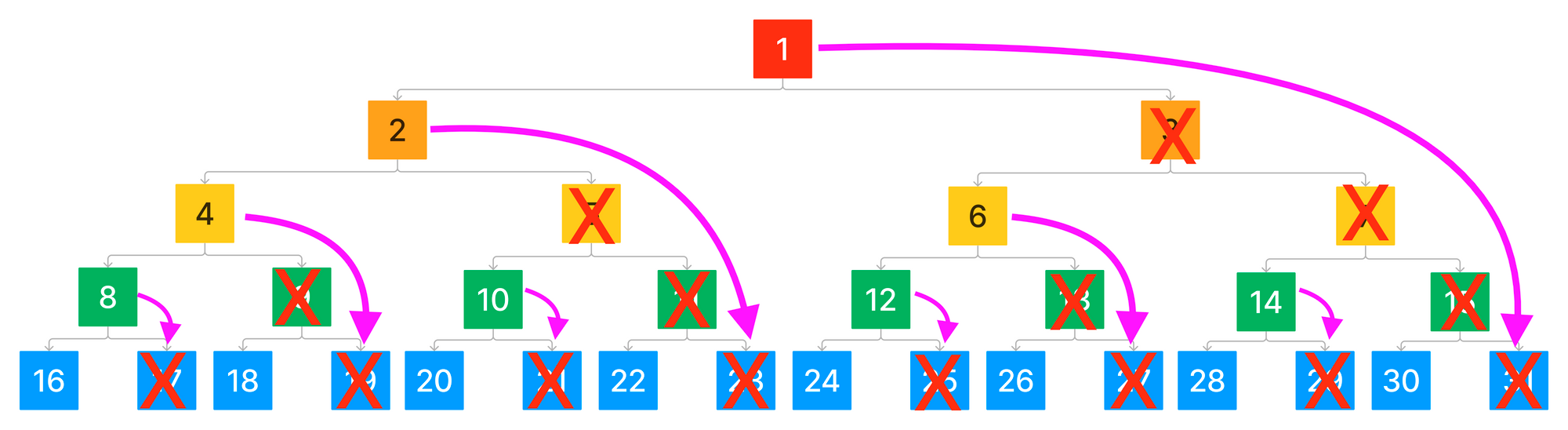
正如我们所看到的,由于根声明承诺了整个轨迹,因此永远无法明确地对其进行防御。可以对根声明进行的唯一移动是不作为或攻击它。
指令步骤(Instruction Step)
在游戏的最大深度处,声明表示对 VM 在单个指令步间隔处的状态的承诺。因为轨迹不能再进一步二分,所以当玩家对这些声明进行有效移动时(移动中定义的有效),玩家的唯一选择是在链上执行 VM 步骤以反驳父节点。如果 VM 步骤证明父节点正确,则父节点将保持未反驳状态。
争端游戏中的声明都是关于 VM 状态的。在指令步骤中,prestate 作为可信输入嵌入到 VM 中,供程序说出关于作为退出代码的内容,而不是将输出根声明直接耦合到 VM。
用于确定从上述部分进行的移动是攻击、防御还是不作为的相同规则适用于树底层的声明。但是,玩家不会调用attack或defend
,而是调用step函数。step函数将找到指令步骤的 pre 或 post 状态,这取决于该移动是攻击还是防御,方法是向上遍历声明的 DAG,直到达到承诺其想要的轨迹索引的声明。
如果移动是攻击,则保证 prestate 存在于祖先中,而 post state 是父节点。
如果移动是防御,则保证 poststate 存在于祖先中,而 prestate 是父节点。
有一个特殊的规则,即如果承诺轨迹索引 0 的声明被攻击,则 prestate 是绝对 Prestate。绝对 prestate 作为可信的初始状态嵌入到 VM 的设置状态中。
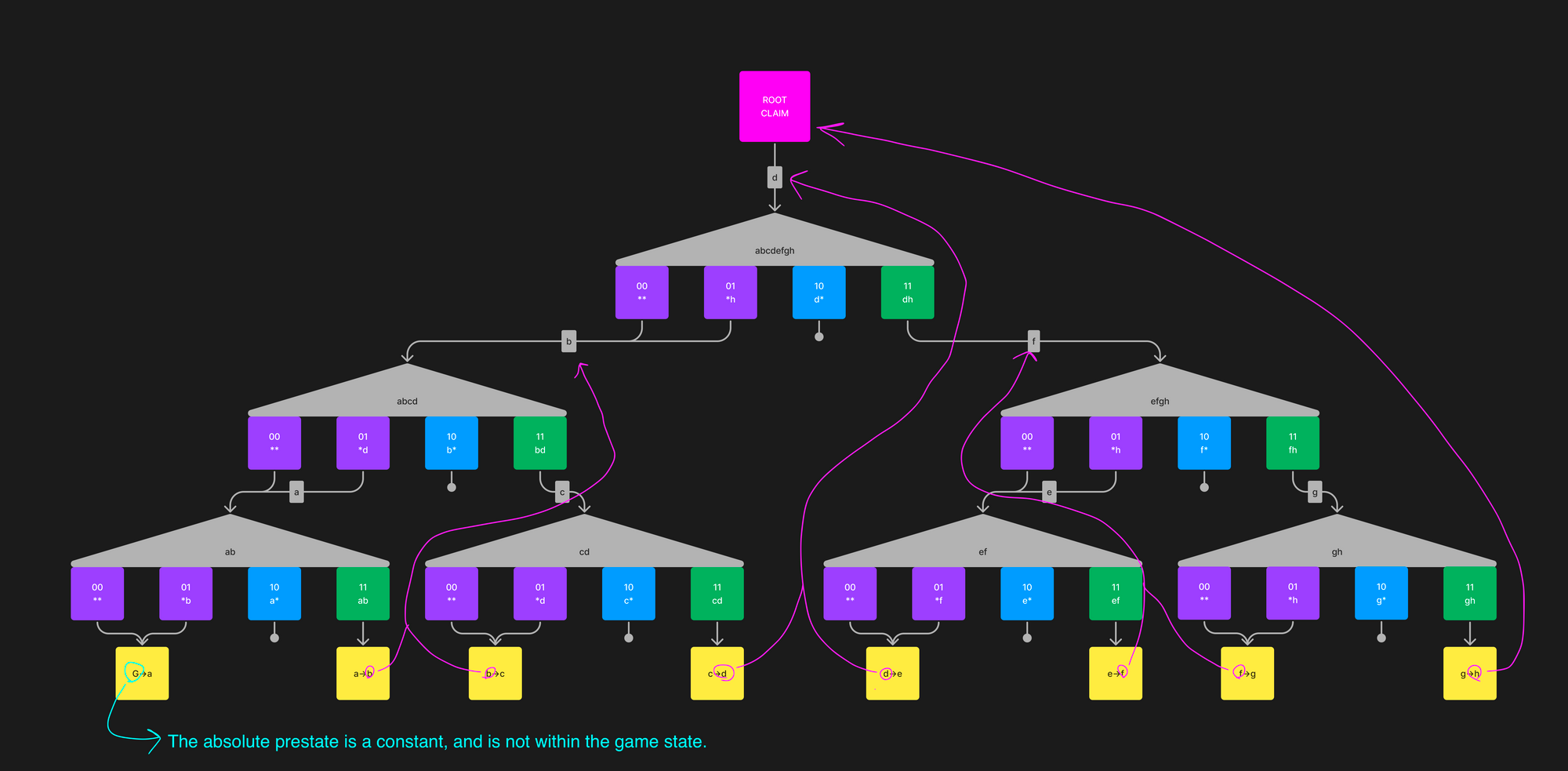
如果指令步骤计算出预期的 post state,则不会发生任何事情。这意味着针对移动的声明是有效的,并且它保持未反驳状态并悬空以在解决中考虑。
如果指令步骤计算出意外的 post state,则父节点将设置为 countered。计算出意外的 post state 或 VM 产生了意外的退出代码,因此不能让该声明悬空。
解决
一旦所有时钟都过期(最长 7 天,但可能更早),就可以解决游戏。为此,我们希望找到最左边、未争议且未被反驳的声明,并检查其深度。
如果最左边未争议的声明的深度为偶数,则根声明解析为 true 。
如果最左边未争议的声明的深度为奇数,则根声明解析为 false 。
这样,我们可以表明诚实玩家的存在将始终导致游戏以对其轨迹的看法有利的方式解决。例如,让我们看一个具有诚实根声明的游戏,其中不诚实挑战者的轨迹在 midpoint → midpoint + 1 指令之间的状态转换中发散。
.png?table=block&id=927d06d4-0042-44bb-a176-f689262b1329&spaceId=5dbe4153-f446-45c1-a5f5-0d60db204c4c&width=2000&userId=&cache=v2)
opposing 玩家已经二分到 gindex 24,它承诺轨迹指令7 → 8
的状态转换的后状态。不诚实的玩家无法执行 step,因为它证明了 gindex 24 处的声明是正确的,从而使诚实挑战者的声明未被争议。在此游戏状态下,它被认为是位于最左边的未争议节点。
其他不诚实的轨迹可能会进入并填充整个左子树,但是由于 step 函数可以证明所有这些轨迹都不正确,因此,假设存在诚实的参与者,不诚实的参与者无法锁定更左边且未争议的声明。
.png?table=block&id=fccdba11-d1a7-444b-876d-280a44049dfc&spaceId=5dbe4153-f446-45c1-a5f5-0d60db204c4c&width=2000&userId=&cache=v2)
我们还可以对具有无效根声明的游戏显示相同的内容。因为此游戏中没有未争议的节点,因此没有“最左边、未争议”的声明,所以挑战者将始终赢得胜利。假设有一个正确的 VM / 绝对 Prestate,不诚实的叶节点声明始终可以通过 step 函数进行反驳,因此他们可以反驳游戏中遇到的任何不诚实的单指令声明。
.png?table=block&id=9db3dc66-6d99-44a8-b6f8-1708df17d3a1&spaceId=5dbe4153-f446-45c1-a5f5-0d60db204c4c&width=2000&userId=&cache=v2)
绑定(Bonding)
Bond 对于朝着正确的方向推动参与者的行为并将游戏投入生产至关重要。在二分游戏中创建的每个声明都必须附加一个 bond,并且该 bond 必须能够涵盖游戏中下一步移动的成本(无论是常规移动还是指令步)。原因很简单:声明在游戏解决之前没有任何明确的真理概念,因此,如果声明解析为 false,则必须涵盖潜在反驳的成本。这些 bond 有两个重要的目的:
诚实的玩家有动力反驳不正确的声明,因为他们知道在游戏解决后,他们将收到附加到他们反驳的声明上的 bond。
不诚实的玩家一开始就没有动力创建不诚实的声明,因为他们知道在游戏解决后,他们的 bond 将被没收。
声明 bond 在创建时很难准确地定价,但是通过一些关键的设计选择,可以很好地解决此问题。创建声明时,其 bond 旨在涵盖可能的反驳声明的成本 - 可以在对手的国际象棋时钟耗尽之前的任何时间提出该反驳声明。这意味着 bond 的大小必须通过启发式方法确定;基本费用可能会波动,具有非恒定 gas 成本的函数可能会增加价格(即,迭代扩展数组),等等,这些都可能导致 bond 抵押不足的情况。为了解决这个问题,可以实施几个系统:
-
基本费用波动预言机 - 我们不需要依赖于即时基本费用来确定 bond 的成本(以 ETH 为单位),而是可以跟踪 L1 基本费用在一段时间内的较大波动次数。此启发式方法对于大多数情况来说都足够好,但是仅靠它并不能涵盖所有必要的边缘情况。
-
重新抵押 - 如果 bond 抵押不足,并且看不到抵押不足的结束(即,一个积累了相当于一个小国规模的财富的恶意方能够将 L1 基本费用维持在 > 5000 连续 5 天),必须有一种机制供游戏玩家验证对手的 bond 是否抵押不足,取消暂停另一位玩家的时钟,并要求对手尽快重新抵押他们的 bond。
-
降低动态 gas 成本 - 我们可以控制我们可以控制的东西,其中一个因素是争端游戏合约中函数的时间复杂度。正在认真努力避免二分游戏合约中的循环和其他非恒定时间操作,以降低 bond 定价的复杂性。通过确保 bond 操作的成本保持恒定或易于推导,我们可以更轻松地计算给定声明的 bond 值。
-
更多启发式方法 - 正如你可能看到的那样,声明 bond 大小的估计永远不会是完美的,但是我相信通过足够的工作,我们可以得到一个“好的”估计。只要安全得到保证,活跃度就是我们需要进行权衡的地方。可能有助于推导 bond 价格的更多启发式方法可能是过去一个月移动的平均成本、有关游戏状态的本地数据(即,基于函数将执行的循环迭代次数提供缓冲区)等等。
词汇表
| 术语 | 定义 |
| 声明(Claim) | 声明是对解析为 true 或false的信息的承诺。 |
| 根声明(Root Claim) | 根声明是争端游戏中的起始声明。 |
| 广义索引(Generalized Index) | 2^{depth} + index_at_depth |
| 绝对 Prestate | VM 的隐式约定的设置状态。 |
- 原文链接: vexil.notion.site/Disput...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 翻译
- 学分: 0
- 分类: 以太坊
- 标签: dispute games bisection game 争议解决 Optimism MIPS 状态转换函数 op-program
- Base链的下一篇章 1062 浏览
- Timelock Guard - Optimism 201 浏览
- 第九季:从实验到组织 - Optimism 760 浏览
- OP Enterprise 介绍 - Optimism 306 浏览
- 新的 Optimism 文档 - Optimism 993 浏览
- Optimism Collective 当前的治理提案流程 941 浏览
- 本章程概述了安全委员会的结构及其参与者的职责 907 浏览
- Flashblocks:深度解析 - OP Mainnet 上的 250 毫秒预确认 - Optimism 1148 浏览
- Layer2 网络治理回顾 #60 1671 浏览
- Layer2 网络治理回顾 #59 (2025年7月7日) 1917 浏览
- Layer2 治理回顾 #58 (2025年6月30日) 2411 浏览
- Optimism 对比 Polygon:哪个以太坊二层网络适合你? 1349 浏览

