一个密文，多个消息：FHE中的SIMD操作

一个密文，多条消息：FHE 中的 SIMD 操作

全同态加密 (FHE) 承诺了一项革命性的能力：在加密数据上执行任意计算，而无需对其进行解密。 这一突破实现了安全的云计算，即使在处理过程中，敏感数据也能得到保护。 然而，早期的 FHE 方案面临着一个关键的瓶颈。 考虑一个简单的任务，例如将两个长度为 1000 的加密向量相加。 这将需要 1000 个单独的同态加法，每个加法都涉及对大型多项式进行昂贵的运算。 对于处理海量数据集的实际应用，这种逐个元素的方法会产生过高的计算开销。

现代 FHE 方案（如 BGV、BFV 和 CKKS）通过一个优雅的数学洞察力解决了这一挑战：它们可以将多个明文值打包到单个密文中，并同时对所有打包的值执行操作。

这些方案不是加密单个数字，而是：

• 将数百或数千个值打包到单个密文中的“槽”中
• 执行并行影响所有槽的同态运算
• 支持复杂的数据移动操作，如旋转和排列

这种 单指令多数据 (SIMD) 方法将 FHE 从一种理论上的好奇转变为一种实用的工具。 单个同态乘法现在可以一次处理整个向量，从而实现几个数量级的加速。

本文探讨了这些 SIMD 运算背后的数学基础。 我们将看到代数和数论中的抽象概念如何结合起来，为并行同态计算创建一个强大的框架。 虽然数学很复杂，但理解这些基础知识对于实现高效的 FHE 应用程序和突破加密计算的可能性至关重要。

数学基础

本文假设你熟悉群和环的基础知识，例如分配律和具有单位元的环的基本性质。 如果你使用过基本群论，那么你应该没问题。

理想

定义。 设 $R$ 为一个环。 子集 $I \subseteq R$ 称为理想，当：

1. $(I, +)$ 构成 $(R, +)$ 的一个子群
2. 对于任何 $r \in R$ 和 $a \in I$， $r \times a$ 和 $a \times r$ 都属于 $I$

第二个条件使理想变得特殊，它们“吸收”与环中任何元素的乘法。 这就像拥有一个数学黑洞，可以吸引你与之相乘的任何东西。

例子。 在整数 $\mathbb{Z}$ 中，考虑 $n$ 的所有倍数的集合 $n\mathbb{Z} = {nk \mid k \in \mathbb{Z}}$。 这构成了一个理想，因为将 $n$ 的任何倍数乘以任何整数都会得到 $n$ 的另一个倍数。

主理想

主理想是最简单的一种，由单个元素生成。 给定 $a \in R$，我们可以创建理想

$(a) = {r \times a \mid r \in R}$.

这捕获了包含 $a$ 的最小理想。 这是你可以通过将 $a$ 乘以环中的元素获得的所有东西。

构建新环：商

给定一个环 $R$ 和一个理想 $I$，我们可以构造一个全新的环，称为商环 $R/I$。

$R/I$ 的元素是陪集，可以将它们视为 $a + I = {a + i \mid i \in I}$ (对于 $a \in R$) 的等价类。 我们通过以下方式定义对这些陪集的操作：

• 加法： $(a + I) + (b + I) = (a + b) + I$
• 乘法： $(a + I) \times (b + I) = (a \times b) + I$

例子：

1. $\mathbb{Z}/n\mathbb{Z}$：这给了我们熟悉的“时钟算术” - 模 $n$ 的整数，元素为 ${0, 1, 2, \ldots, n-1}$。

2. 多项式商：取 $R = \mathbb{F}[X]$， $I = (f(X))$，我们得到模 $f(X)$ 的多项式 - 本质上是多项式算术，我们在其中使用关系 $f(X) = 0$ 替换高次幂。

单位根

在任何环 $R$ 中，$n$ 次单位根是一个元素 $\zeta$ 使得 $\zeta^n = 1$。 但我们特别感兴趣的是本原 $n$ 次单位根 $\zeta^k \neq 1$，对于所有正整数 $k < n$。

这是一个关键的洞察：$\zeta_n^k$ 是本原 $n$ 次单位根当且仅当 $\gcd(k, n) = 1$。

为什么这样有效

设 $\zeta_n = e^{2\pi i / n}$。 $n$ 次单位根是 $n$ 个不同的幂 $\zeta_n^0, \zeta_n^1, \ldots, \zeta_n^{n-1}$，因此 $\zeta_n$ 本身是本原的。

关键的观察是 $\zeta_n^a = 1$ 当且仅当 $a$ 可被 $n$ 整除。 原因是：写成 $n = aq + r$，其中 $0 \leq r < a$。 那么 $\zeta_n^r = \zeta_n^{n-aq} = 1$。 但由于 $\zeta_n$ 是本原的，因此这仅在 $r = 0$ 时发生。

现在，如果 $\gcd(k, n) = d > 1$，那么 $(\zeta_n^k)^{n/d} = \zeta_n^{k \cdot n/d} = \zeta_n^{n \cdot k/d} = 1$，所以 $\zeta_n^k$ 不是本原的。

反之，如果 $\gcd(k, n) = 1$ 且 $(\zeta_n^k)^r = 1$，那么 $n$ 除 $kr$。 由于 $n$ 和 $k$ 互质，因此我们必须使 $n$ 除 $r$。 这意味着 $\zeta_n^k$ 的第一个等于 $1$ 的正幂是 $n$ 次幂。

Euler总计函数 $\varphi(n)$ 准确地计算了这些“好的”指数 - 与 $n$ 互质的正整数 $k \leq n$。 因此，恰好有 $\varphi(n)$ 个本原 $n$ 次单位根。

例子。 在复数中，本原 $n$ 次单位根恰好是 $e^{2\pi i k/n}$，其中 $\gcd(k, n) = 1$。

Euler总计函数 $\varphi(n)$ 计算高达 $n$ 的与 $n$ 互质的正整数： $\varphi(n) = |{1 \leq k \leq n \mid \gcd(k, n) = 1}|$

一个具体的例子：$\mathbb{F}_{3^2}$ 中的 8 次单位根

让我们计算一个具体的例子。 我们将在二次扩展中找到 8 次单位根

$\mathbb{F}_{3^2} = \mathbb{F}_3[X]/(X^2+1)$

我们应该期望有多少个根？

在大小为 $q$ 的有限域中，乘法群 $\mathbb{F}_q^{\times}$ 的阶数为 $q-1$。

• 如果 $n$ 与 $q-1$ 互质，那么 $\mathbb{F}_q$ 仅包含平凡的 $n$ 次单位根：仅 $1$。
• 如果 $n$ 除 $q-1$，则该域包含恰好 $n$ 个不同的 $n$ 次单位根，形成该阶的唯一子群。

这里，$q = 9$，所以 $q-1 = 8$。 由于 $8$ 除 $8$，因此我们期望所有八个 8 次单位根存在于 $\mathbb{F}_{3^2}^{\times}$ 中。

找到全部八个根

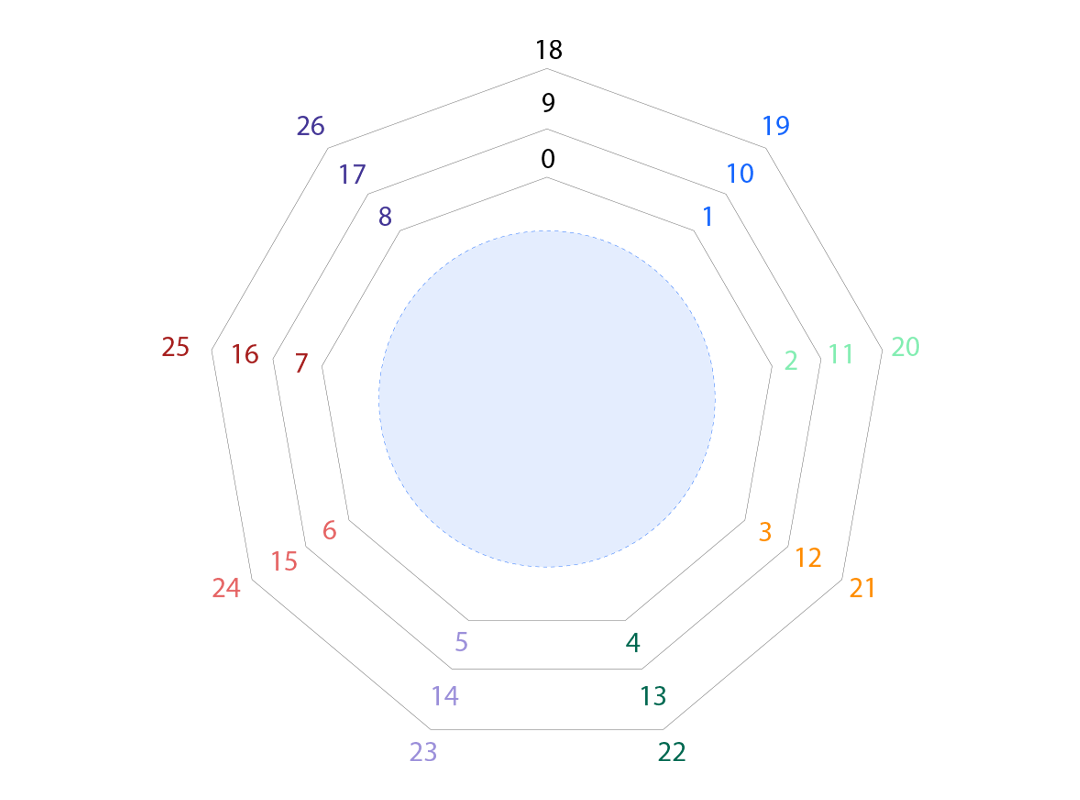
我们将 $\mathbb{F}_{3^2}$ 的元素写成 $a+bx$ 的形式，其中 $a, b \in {0, 1, 2}$，其中 $x^2 = -1 \equiv 2 \pmod{3}$。

使用 Sage（或者如果你感觉有野心，也可以手动）：

R.<t> = PolynomialRing(GF(3))
F.<x> = GF(3^2, modulus = t^2 + 1)

roots8 = [z for z in F if z^8 == 1]
print(roots8)

这给了我们：

$1, x + 1, 2x, 2x + 1, 2, 2x + 2, x, x + 2$

$\mathbb{F}_{3^2}$ 中 $z^8 = 1$ 的所有八个解。

哪些是本原的？

当元素的阶数恰好为 $8$ 时，该元素是本原的。 Euler总计告诉我们 $\varphi(8) = 4$，因此我们的八个根中恰好有四个应该是本原的。

g = F.multiplicative_generator()
primitive = [g^k for k in (1,3,5,7)]
print(primitive)

这揭示了：

${x+1, 2x+1, 2x+2, x+2}$

这四个是我们的本原 8 次根。 剩余根的阶数为 1、2 或 4。

分圆多项式：收集本原根

$n$ 次分圆多项式 $\Phi_n(X)$ 旨在准确捕获本原 $n$ 次单位根。 在有理数上：

$\Phin(X) = \prod{\substack{1 \leq k \leq n \ \gcd(k, n) = 1}} (X - \zeta_n^k)$

该多项式的阶数为 $\varphi(n)$ - 每个本原根一个因子。

让我们构造 $\Phi_8(X)$

根据定义：

$\Phi8(X) = \prod{\substack{1 \leq k \leq 8 \ \gcd(k, n) = 1}} (X-\zeta_8^k) = X^4+1$

这给了我们一个在 $\mathbb{Q}$ 上不可约的四次首一多项式（阶数 $\varphi(8) = 4$）。

同态：结构保持映射

群同态

群 $(G, \cdot)$ 和 $(H, *)$ 之间的群同态是一个函数 $\phi: G \to H$，它尊重群运算：

$\phi(a \cdot b) = \phi(a) * \phi(b)$

每个同态都有两个重要的子集：

• 核： $\ker(\phi) = {g \in G \mid \phi(g) = e_H}$ （映射到单位元的元素）
• 像： $\text{im}(\phi) = {\phi(g) \mid g \in G}$ (所有可能的输出)

两者都形成各自群的子群。

环同态

类似地，环 $(R, +, \times)$ 和 $(S, \oplus, \odot)$ 之间的环同态保留了两种运算：

• $\psi(a + b) = \psi(a) \oplus \psi(b)$
• $\psi(a \times b) = \psi(a) \odot \psi(b)$
• $\psi(1_R) = 1_S$ （保留乘法单位元）

同构：当结构“相同”时

当同态是双射时，我们称其为同构。 从代数的角度来看，同构结构本质上是相同的 - 它们具有相同的“形状”。

自同构是从结构到其自身的同构。 群 $G$ 的所有自同构的集合在组合下形成一个群，记为 $\text{Aut}(G)$。

中国剩余定理：一个强大的分解

设 $R$ 是具有单位元的交换环，$I_1, I_2, \ldots, I_n$ 为互素理想（意味着 $I_i + I_j = R$ 只要 $i \neq j$）。 定义 $I = I_1 \cap I_2 \cap \cdots \cap I_n$。 那么我们有一个同构：

$R/I \cong (R/I_1) \times (R/I_2) \times \cdots \times (R/I_n)$

为什么这样有效

我们将通过对理想的数量进行归纳来证明这一点。

基本情况 ($n=2$)： 设 $I, J$ 为互素理想，其中 $I + J = R$。 我们想证明 $R/(I \cap J) \cong (R/I) \times (R/J)$。

考虑自然映射：

$\varphi: R \to (R/I) \times (R/J), \quad x \mapsto (x+I, x+J)$

根据第一同构定理，足以证明 $\varphi$ 是满射的，核为 $I \cap J$。

环的第一同构定理：如果 $\varphi\colon R \longrightarrow S$ 是核为 $\ker(\varphi)$ 的满射环同态，则 $\varphi$ 导出自然环同构

$\varphi: R/\ker(\varphi) \xrightarrow{\sim} S, \qquad r + \ker(\varphi)\mapsto \varphi(r)$.

核验证： 我们有

$x \in \ker\varphi \Leftrightarrow (x+I, x+J) = (0+I, 0+J) \Leftrightarrow x \in I \text{ 且 } x \in J \Leftrightarrow x \in I \cap J$

满射： 取任意 $(x_1+I, x_2+J) \in (R/I) \times (R/J)$。 由于 $I + J = R$，我们可以找到 $y_1 \in I$ 和 $y_2 \in J$，其中 $y_1 + y_2 = 1$。

定义 $x = x_1 + y_1(x_2 - x_1) = x_2 - y_2(x_2 - x_1)$。

那么 $x \equiv x_1 \pmod{I}$ 且 $x \equiv x_2 \pmod{J}$，所以 $\varphi(x) = (x_1+I, x_2+J)$。

归纳步骤： 假设该定理对于 $n$ 个理想成立。 对于 $n+1$ 个互素理想 $I1, \ldots, I{n+1}$，观察到 $I1, \ldots, I{n-1}, In \cap I{n+1}$ 是两两互素的。

根据归纳假设：

$R/I \cong (R/I1) \times \cdots \times (R/I{n-1}) \times (R/(In \cap I{n+1}))$

将基本情况应用于 $In$ 和 $I{n+1}$：

$R/(In \cap I{n+1}) \cong R/In \times R/I{n+1}$

将这些结合起来得到所需的结果。

全同态加密中的 SIMD 运算

现在我们进入激动人心的部分 - 所有这些抽象代数如何在加密数据中实现强大的并行计算。

我们的多项式存在的地方

我们从商环 $A = \mathbb{Z}[X]/(\Phi_m(X))$ 开始，其中 $\Phi_m(X)$ 是 $m$ 次分圆多项式。 这是我们的基本工作区。

在同态加密中，我们不直接加密整数。 相反，我们在作为明文空间的素域 $\mathbb{F}_p = \mathbb{Z}/p\mathbb{Z}$ 上工作。 将所有系数模 $p$ 归约得到明文环：

$A_p = \mathbb{F}_p[X]/(\overline{\Phi_m}(X))$

横线只是提醒我们已经完成了模归约。

分圆分解的魔力

这里是数论提供一些美妙的东西的地方。 只要 $p$ 不能整除 $m$，分圆多项式 $\Phi_m(X)$ 就可以在 $\mathbb{F}_p$ 上完全分解为相等阶的不可约片段：

$\overline{\Phi_m}(X) = F_1(X) F_2(X) \cdots F_n(X) \bmod p$

每个 $F_i$ 都是不可约的，阶数为 $d = \text{ord}_m(p)$ - $p$ 模 $m$ 的乘法阶。

让我们选择任何不可约因子，例如 $F_1(X)$，并定义：

$E = \mathbb{Z}_p[X]/(F_1(X)), \quad \eta = [X \bmod F_1(X)] \in E$

由于 $F_1(X)$ 是不可约的，因此 $E$ 变为具有 $p^d$ 个元素的域。 $E$ 中的每个元素都可以写成 $f(\eta)$ 形式，其中 $f(X)$ 是某个多项式。 请注意，$\eta$ 是 $F_1(X)$ 的根，使其成为本原 $m$ 次单位根。 为什么陪集 η=[X]η=[X]η=[X] 立即成为 F1F1F1 的根：形成商环

E=Zp[X]/(F1(X))E=Zp[X]/(F1(X))E = \mathbb{Z}_p[X]/(F_1(X))

只不过是在环内声明多项式 F1(X)F1(X)F_1(X) 现在等于零。

• 投影 π:Zp[X]→Eπ:Zp[X]→E\pi:\mathbb{Z}_p[X]\to E 将每个多项式发送到它的陪集。 写成

  η:=π(X)=X+(F1(X)).η:=π(X)=X+(F1(X)).\eta := \pi(X) = X + (F_1(X)).

这个 ηηη 是“XXX 的像”。

• 因为 F1(X)F1(X)F_1(X) 在我们进行因式分解的理想中，所以它的陪集为 000： π(F1(X))=0.π(F1(X))=0.\pi\bigl(F_1(X)\bigr)=0.

但 πππ 是同态，因此 π(F1(X))=F1(π(X))=F1(η)π(F1(X))=F1(π(X))=F1(η)\pi\bigl(F_1(X)\bigr)=F_1\bigl(\pi(X)\bigr)=F_1(\eta)。 因此 F1(η)=0F1(η)=0F_1(\eta)=0 在 EEE 中。 通过构造，ηηη 的行为完全像 F1F1F1 的根。

多项式 Φm(X)‾Φm(X)‾\overline{\Phi_m}(X) 在 EEE 中具有 φ(m)φ(m)\varphi(m) 个不同的根，特别是 ηjηj\eta^j，对于单位群 Zm∗Zm∗\mathbb{Z}_m^* 中的每个 jjj。 这些根均匀地分布在不可约因子之间，每个因子精确地得到 ddd 个根。

要理解分布，请考虑子群：

H=⟨pˉ⟩⊂Zm∗,pˉ:=[pmodm]H=⟨pˉ⟩⊂Zm∗,pˉ:=[pmodm]H = \langle \bar{p} \rangle \subset \mathbb{Z}_m^*, \quad \bar{p} := [p \bmod m] 这个子群的阶数为 ddd，并且包含 1,pˉ,pˉ2,…,pˉd−11,pˉ,pˉ2,…,pˉd−11, \bar{p}, \bar{p}^2, \ldots, \bar{p}^{d-1}。

当我们形成商群 Zm∗/HZm∗/H\mathbb{Z}_m^*/H 时，我们得到 n=φ(m)/dn=φ(m)/dn = \varphi(m)/d 个不同的陪集：

kH={k⋅h:h∈H}⊂Zm∗kH={k⋅h:h∈H}⊂Zm∗kH = {k \cdot h : h \in H} \subset \mathbb{Z}_m^*

从每个陪集中选择代表 k1,k2,…,knk1,k2,…,knk_1, k_2, \ldots, k_n，我们可以安排使得每个 Fi(X)Fi(X)F_i(X) 恰好有 ddd 个根 ηkηk\eta^k，其中 k∈kiHk∈kiHk \in k_i H。

中国剩余定理的突破

现在是回报的时候了。我们可以为每个因子建立同构：

Zp[X]/(Fi(X))→E,[f(X)modFi(X)]↦f(ηki)Zp[X]/(Fi(X))→E,\mathbb{Z}_p[X]/(F_i(X)) \to E, \quad [f(X) \bmod F_i(X)] \mapsto f(\eta^{k_i})

将其与以下事实结合：

$$ \begin{array}{rcl} A{p} & \longrightarrow & \displaystyle \Bbb Z{p}[X]\bigl/!\bigl(F{1}(X)\bigr) \;\times\; \cdots \;\times\; \Bbb Z{p}[X]\bigl/!\bigl(F{n}(X)\bigr) \[6pt] f(x) & \longmapsto & \bigl(\, [\,f(X)\bmod F{1}(X)\,],\; \ldots,\; [\,f(X)\bmod F_{n}(X)\,] \bigr), \end{array} $$

为我们提供了关键的同构：

$A_p \to E^n, \quad f(x) \mapsto (f(\eta^{k_1}), \ldots, f(\eta^{k_n}))$

这是关键的洞察：我们可以通过在 $A_p$ 中进行环运算来对 $E^n$ 中的向量执行分量运算！

如果我们有：

$$ \begin{gathered} a \in A_p \leftrightarrow (\alpha_1, \ldots, \alpha_n) \in E^n \ b \in A_p \leftrightarrow (\beta_1, \ldots, \beta_n) \in E^n \end{gathered} $$

然后：

$$ \begin{gathered} a + b \leftrightarrow (\alpha_1 + \beta_1, \ldots, \alpha_n + \beta_n) \ a \cdot b \leftrightarrow (\alpha_1\beta_1, \ldots, \alpha_n\beta_n) \end{gathered} $$

使用数论变换（NTT）在 $A_p$ 中的系数表示和 $E^n$ 中的槽表示之间进行转换在计算上非常简单。

分圆多项式示例：NTT 实现

让我们通过一个具有特定参数的具体示例：

• $m=8$, $\varphi(m)=4$, $p=3$, $d=2$ （因为 $3^2 \equiv 1 \bmod 8$），$n=\varphi(m)/d=2$

  分圆多项式分解

  第 8 个分圆多项式是 $\Phi_8(X) = X^4 + 1$。在 $\mathbb{F}_3[X]$ 上，这可以分解为：

  R.<X = PolynomialRing(GF(3))
  factor = (X^4 + 1).factor()
  print(factor)

  $X^4 + 1 = (X^2 + X + 2)(X^2 + 2X + 2) \quad \text{in } \mathbb{F}_3[X]$

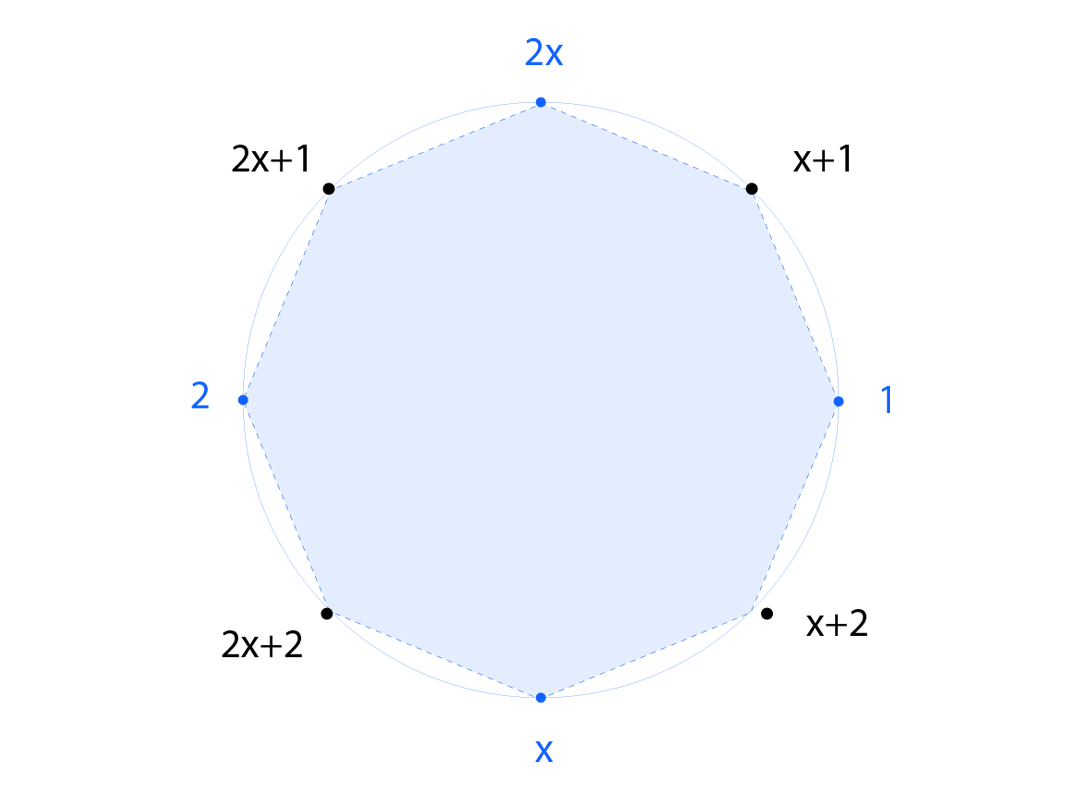
四个本原 8 次单位根是：

${\alpha+1, 2\alpha+1, 2\alpha+2, \alpha+2} \subset E$

每个不可约二次多项式“拥有”其中两个：

多项式	$E$ 中的根
$X^2 + X + 2$	${2\alpha+1, \alpha+1}$
$X^2 + 2X + 2$	${2\alpha+2, \alpha+2}$

陪集与中国剩余定理同构

陪集结构由以下因素决定：

• 子群：$H = \langle 3 \rangle = {1, 3} \subset \mathbb{Z}_8^*$
• 商：$\mathbb{Z}_8^*/H = {{1, 3}, {5, 7}}$
• 代表：$k_1 = 1$, $k_2 = 5$

这给了我们同构：

$A_3 = \mathbb{F}_3[X]/(X^4+1) \xrightarrow{\sim} E^2$ $f(x) \mapsto (f(\eta^{k_1}), f(\eta^{k_2})) = (f(\alpha+1), f(2\alpha+2))$

逆变换：槽值到多项式

我们想要编码以下槽值：

$f(\eta)=2, \qquad f(\eta^5)=1,$

其中 $\eta = \alpha+1$。

多项式表示

$A_3$ 中的任何多项式都有唯一的代表：

$f(X)=a_0+a_1X+a_2X^{2}+a_3X^{3},\qquad ai\in\mathbf F{3}.$

这意味着我们需要对我们的函数进行 4 次求值才能使用 NTT 进行插值。因为 Frobenius 自同构 $x \mapsto x^{3}$ 修复了每个 $\Bbb F_{3}$ 分量，所以我们有：

$f(\eta)= 2 = f(\eta^{3}),\qquad f(\eta^{5})= 1 = f(\eta^{7})$

设置逆 NTT

的确

$\omega:=\eta^{2}=2x$, $\omega^{2}=(2x)^{2}=4x^{2}=x^{2}=2$,

$\omega^{4}=2^{2}=1$,

并且 $\omega\neq1$, $\omega^{2}\neq1$，所以 $\omega$ 是一个本原 4 次单位根。

我们需要 $f$ 在 $\eta$ 的奇数次幂处求值：

${\,\eta^{1},\eta^{3},\eta^{5},\eta^{7}} ={\,\eta\,\omega^{0},\,\eta\,\omega^{1},\,\eta\,\omega^{2},\,\eta\,\omega^{3}}.$

分解出 $w^{j}$ 并将其吸收到系数中：

$$ \begin{aligned} f(w^{2k+1}) &=\sum{j=0}^{3} a{j}(w^{2k+1})^{j}\[4pt] &=\sum{j=0}^{3} a{j}\,w^{j}\,(\omega^{k})^{j} \;=\; \sum{j=0}^{3} b{j}\,\omega^{jk}, \end{aligned} $$

因此

• Twist（扭曲） $b = D{\text{in}}\,a$ 其中 $D{\text{in}}=\operatorname{diag}(1,w,w^{2},w^{3})$。
• NTT $y = F\,b$ 其中 $F_{k,j}=\omega^{jk}$。

逆 NTT 后的 Untwisting（解扭）

逆 NTT 返回 $b = F^{-1}y$。删除 twist（扭曲）：

$a{j}=b{j}\,w^{-j}=b_{j}\,w^{8-j}$

所有系数现在都回到了 $\mathbb{F}_{3}$ 中。

因此：

$f(X)=a_0+a_1X+a_2X^{2}+a_3X^{3}=X^{3}+X,$

有效性检查

我们可以通过检查槽值来验证获得的多项式是否正确：

• 槽 0：$f(X) \bmod (X^2 + X + 2) = 2$
• 槽 1：$f(X) \bmod (X^2 + 2X + 2)= 1$

一切都与给定的槽值匹配，确认重构是正确的。

添加第二个多项式

让我们为以下情况进行相同的变换

$f(\eta)=x+2, \qquad f(\eta^5)=2x,$

首先我们找到缺失的评估值

$f(\eta^{3}) = f(\eta)^3 = 2 + 2x,\qquad f(\eta^{7}) = f(\eta^5)^3 = x$

然后经过相同的逆 NTT 过程，我们得到

$f(X)=X + 1$

同态加法

我们有

$X^3 + X \mapsto (2, 1), \qquad X + 1 \mapsto (x+2, 2x)$

让我们检查一下同态加法是否定义良好：

$X^3 + 2X + 1 \mapsto (x+1, 2x+1)$

找到缺失的评估值：

$f(\eta^{3}) = f(\eta)^3 = 1 + 2x,\qquad f(\eta^{7}) = f(\eta^5)^3 = 1 + x$

并运行逆 NTT 以重构多项式

$f(X)=X^3 + 2X + 1$

 F3  = GF(3)
 F9.<x = GF(9, modulus = x^2 + 1)
 R.<X = PolynomialRing(F3)

 slot0, slot1 = (2, 1)

 w   = x + 1
 omega = w^2
 omega_inv = omega.inverse()

 y0, y2 = F9(slot0), F9(slot1)
 y1, y3 = y0^3, y2^3
 y      = [y0, y1, y2, y3]

 b = []
 for j in range(4):
     s = F9.zero()
     for k in range(4):
         s += y[k] * (omega_inv)^(j*k)
     b.append(s)

 a = [F3(b[j] * w^(8 - j))  for j in range(4)]

 f = (a[0] + a[1]*X + a[2]*X^2 + a[3]*X^3) % (X^4 + 1)

 print(f)

Galois 自同构：数据移动的关键

要理解如何在槽之间移动数据，我们回到环 $A = \mathbb{Z}[X]/(\Phi_m(X))$，其中 $x$ 表示 $A$ 中 $X$ 的图像。

对于每个 $j \in \mathbb{Z}_m^*$，我们可以定义：

$\theta_j : A \to A, \quad \theta_j(f(x)) = f(x^j)$

这是定义明确的，因为如果 $\gcd(j,m) = 1$，那么每当 $\omega$ 是本原 $m$ 次单位根时，$\omega^j$ 也是。这意味着如果 $\Phi_m(\omega) = 0$，那么 $\Phi_m(\omega^j) = 0$ 也是，从而得出：

$\Phi_m(X) \mid \Phi_m(X^j) \quad \text{in } \mathbb{Z}[X]$

这些映射具有自然的群结构：由于 $(x^j)^k = x^{jk}$ 在 $A$ 中，我们有：

$\theta_j \circ \thetak = \theta{jk}$

这给了我们一个单射群同态：

$\mathbb{Z}_m^* \hookrightarrow \text{Aut}(A), \quad j \mapsto \theta_j$

这些 $\theta_j$ 映射正是我们分圆扩张的 Galois 自同构。

Frobenius 映射：一种特殊的自同构

Frobenius 自同构值得特别关注：

$\sigma : E \to E, \quad f(\eta) \mapsto f(\eta^p)$

对于每个 $\alpha \in E$，我们有 $\sigma(\alpha) = \alpha^p$。重要的是：

$\alpha \in \mathbb{Z}_p \Leftrightarrow \sigma(\alpha) = \alpha$

在我们 $A_p$ 和 $E^n$ 之间的对应关系下，如果我们令 $\bar{p} = [p \bmod m] \in \mathbb{Z}m^*$ 并应用 $\theta{\bar{p}}$：

$\theta_{\bar{p}}(f(x)) \to(\sigma(f(\eta^{k_1})), \ldots, \sigma(f(\eta^{k_n}))) \in E^n$

这意味着 $\theta_{\bar{p}}$ 在 $E$ 上以槽的方式充当 Frobenius 映射 - 这对于理解旋转至关重要。

一维旋转：使数据移动

考虑一个元素 $g \in \mathbb{Z}_m^$ 使得 $1, g, g^2, \ldots, g^{n-1}$ 形成 $\mathbb{Z}_m^$ 中 $H$ 的完整陪集代表集。这意味着 $g^n$ 必须位于 $H$ 中。

在理想情况下，$g^n = 1$，使用代表 $1, g, \ldots, g^{n-1}$，我们的槽同构变为：

$f(x) \in A_p \leftrightarrow (f(\eta^1), f(\eta^g), \ldots, f(\eta^{g^{n-1}})) \in E^n$

当我们应用 $\theta_g$ 时：

$\theta_g(f(x)) \leftrightarrow (f(\eta^g), f(\eta^{g^2}), \ldots, f(\eta^{g^{n-1}}), f(\eta^1))$

由于最后一个条目环绕到 $f(\eta^1)$，因此自同构 $\thetag$ 将槽向左旋转一个位置！更一般地说，$\theta{g^e}$ 向左旋转 $e$ 个位置，而 $\theta_{g^{-e}}$ 向右旋转 $e$ 个位置。

当 $g^n \neq 1$ 时，事情会变得棘手。如果 $g^n = \bar{p}^s$ 对于某些 $s \in {1, \ldots, d-1}$：

$\theta_g(f(x)) \leftrightarrow (f(\eta^g), f(\eta^{g^2}), \ldots, f(\eta^{g^{n-1}}), \sigma^s(f(\eta^1)))$

这会产生一个旋转，但最后一个槽会被 $\sigma^s$ 扰动。除非第一个槽包含 $\mathbb{Z}_p$ 中的值，否则这不是一个干净的旋转，其中 $\sigma^s$ 的作用是微不足道的。

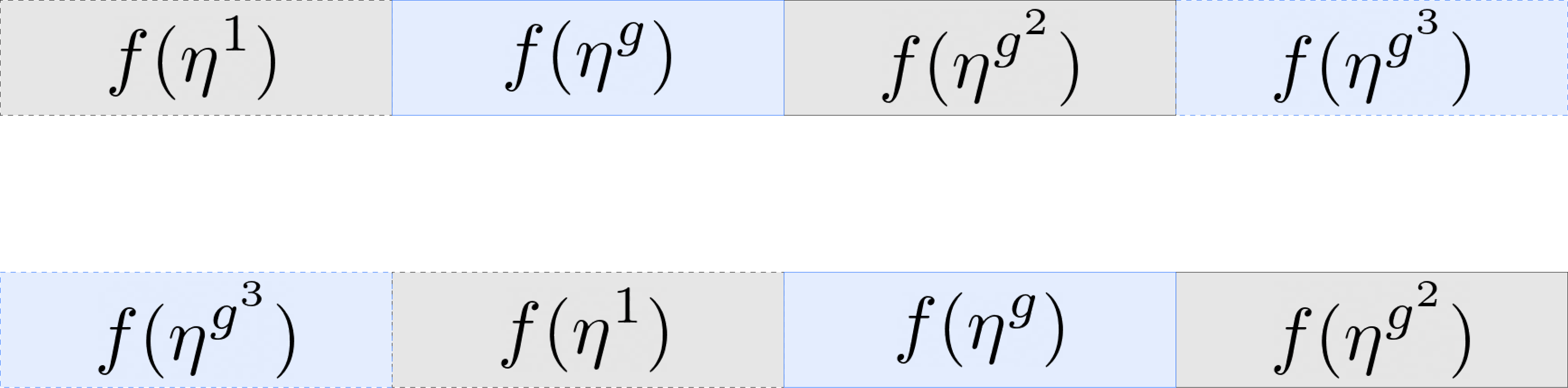
通过掩码进行无损旋转

即使槽包含 $\mathbb{Z}_p$ 之外的值，我们也可以使用巧妙的掩码技术来实现完美的旋转。

对于 $e \in {1, \ldots, n-1}$ 位置的旋转，我们创建掩码元素：

$M_e \in Ap \leftrightarrow (\underbrace{1,\ldots,1}{n-e}, \underbrace{0,\ldots,0}_{e}) \in E^n$

$1-M_e \in Ap \leftrightarrow (\underbrace{0,\ldots,0}{n-e}, \underbrace{1,\ldots,1}_{e}) \in E^n$

对于一个元素 $a \in A_p \leftrightarrow (\alpha0, \ldots, \alpha{n-1}) \in E^n$：

• Mask-then-rotate（掩码然后旋转）左移 $e$ 槽：

$Me \cdot \theta{g^e}(a) \leftrightarrow (\alphae, \ldots, \alpha{n-1}, \underbrace{0,\ldots,0}_{e})$

• Mask-then-rotate（掩码然后旋转）右移 $e$ 槽：

$(1-Me) \cdot \theta{g^{e-n}}(a) \leftrightarrow (\underbrace{0,\ldots,0}_{n-e}, \alpha0, \ldots, \alpha{e-1})$

将这些结合起来可以实现完美的左旋转： $Me \cdot \theta{g^e}(a) + (1-Me) \cdot \theta{g^{e-n}}(a)$

这会产生一个元素，它的槽位正好是将 $a$ 向左旋转 $e$ 个位置后的槽位，无论槽位值是否位于 $\mathbb{Z}_p$之外。

多维运算：超立方体方法

对于更复杂的数据排列，我们可以将我们的 $n$ 个槽位组织成一个多维超立方体。设 $n = n_1 n2 \cdots n\ell$ 是我们的槽位数分解为 $\ell$ 个正整数。

我们选择生成器 $g1,\dots,g\ell \in \mathbb{Z}_m^{*}$，并将陪集代表排列为：

$g_1^{e_1} g_2^{e2}\cdots g\ell^{e_\ell}, \qquad e_i\in[n_i]:={0,\dots,n_i-1}$

这会创建一个具有边长 $(n1,\dots,n\ell)$ 的 $\ell$ 维超立方体，其中每个槽位都有坐标 $(e1,\dots,e\ell)$。

简化轴向旋转

对于每个维度 $i$，Galois 自同构 $\theta_{g_i}$ 将每个超列 $(e1,\dots,e{i-1},*,e{i+1},\dots,e\ell)$ 在第 $i$ 个坐标中向前移动一步。应用 $\theta_{gi^e}$ 移动 $e$ 个位置，而 $\theta{g_i^{-e}}$ 向后移动。

多维掩码

对于没有 Frobenius 扰动的真正旋转，我们使用掩码元素 $M^{(i)}_{e}$，它将每个超列的前 $n_i-e$ 个槽位设置为 1，其他位置设置为 0。

沿第 $i$ 轴向左旋转 $e$ 个位置的公式为：

$M^{(i)}{e}\,\theta{gi^e}(a)\;+\;(1-M^{(i)}{e})\,\theta_{g_i^{e-n_i}}(a)$

使用 Lattigo 在 BGV 中进行 SIMD 运算

此示例演示了使用 Lattigo 库的 BGV API 进行的槽位式同态加法。借助 BGV 强大的 SIMD 功能，我们可以将整个整数向量打包到单个密文中，并行地对每个向量条目执行加密计算，然后在解密后恢复结果。

package main

import (
    "fmt"
    "log"
    "math/rand"
    "time"

    "github.com/tuneinsight/lattigo/v6/examples"
    "github.com/tuneinsight/lattigo/v6/schemes/bgv"
)

func main() {
    paramDef := examples.BGVParamsN12QP109
    params, err := bgv.NewParametersFromLiteral(paramDef)
    if err != nil {
        log.Fatalf("params error: %v", err)
    }

    kgen := bgv.NewKeyGenerator(params)
    sk := kgen.GenSecretKeyNew()
    pk := kgen.GenPublicKeyNew(sk)

    encoder := bgv.NewEncoder(params)
    encryptor := bgv.NewEncryptor(params, pk)
    decryptor := bgv.NewDecryptor(params, sk)
    evaluator := bgv.NewEvaluator(params, nil)

    T := params.PlaintextModulus()
    slots := params.MaxSlots()
    rand.Seed(time.Now().UnixNano())

    a := make([]uint64, slots)
    b := make([]uint64, slots)
    expected := make([]uint64, slots)
    for i := 0; i < slots; i++ {
        a[i] = uint64(rand.Int63n(int64(T)))
        b[i] = uint64(rand.Int63n(int64(T)))
        expected[i] = (a[i] + b[i]) % T
    }

    ptA := bgv.NewPlaintext(params, params.MaxLevel())
    ptB := bgv.NewPlaintext(params, params.MaxLevel())
    if err := encoder.Encode(a, ptA); err != nil {
        log.Fatal(err)
    }
    if err := encoder.Encode(b, ptB); err != nil {
        log.Fatal(err)
    }
    ctA, err := encryptor.EncryptNew(ptA)
    if err != nil { log.Fatal(err) }
    ctB, err := encryptor.EncryptNew(ctB)
    if err != nil { log.Fatal(err) }

    ctC, err := evaluator.AddNew(ctA, ctB)
    if err != nil { log.Fatal(err) }

    ptRes := decryptor.DecryptNew(ctC)
    res := make([]uint64, slots)
    if err := encoder.Decode(ptRes, res); err != nil {
        log.Fatal(err)
    }

    fmt.Printf("i\t a\t b\t (a+b mod T)\t result\t match\n")
    for i := 0; i < slots; i++ {
        fmt.Printf("%d:\t%d\t%d\t%d\t\t%d\t%v\n",
            i, a[i], b[i], expected[i], res[i], res[i] == expected[i])
    }
}

结论

这篇文章中探讨的数学基础揭示了抽象代数如何将全同态加密从一个理论上的好奇心转变为安全计算的实用工具。 我们涵盖的关键见解包括：

代数结构：明文环 $A_p = \mathbb{F}_p[X]/(\overline{\Phi_m}(X))$ 通过分圆分解自然分解为扩展域 $E^n$ 的乘积。这种分解使得基于槽位的打包成为可能。

Galois 自同构：映射 $\theta_j: f(x) \mapsto f(x^j)$ 提供了槽位之间数据移动的机制。这些自同构在根据乘法群 $\mathbb{Z}_m^*$ 排列槽位内容的同时，保留了环结构。旋转技术：干净的旋转需要通过掩码操作仔细处理 Frobenius 映射。超立方体组织将其扩展到多维数据排列，从而实现复杂的数据移动模式。

实际影响：与逐个元素处理相比，这些数学工具提供了几个数量级的加速。单个同态乘法现在可以处理整个向量，从而使 FHE 适用于安全云计算、保护隐私的机器学习和机密数据分析等实际应用。

致谢

这篇文章建立在代数数论和密码学领域数十年的研究基础上。特别感谢 Nigel Smart 和 Frederik Vercauteren 的基础性论文 "全同态 SIMD 运算"，该论文为 FHE 方案中基于槽位的并行计算建立了理论框架。他们的工作表明如何利用分圆多项式算术在同态加密中实现真正的向量化。

实践实施方面的见解在很大程度上借鉴了 Shai Halevi 和 Victor Shoup 的综合著作 "HElib 的设计与实现：同态加密库"，该著作将这些理论进步转化为高效、可用的软件。

• 原文链接： hexens.io/blog/simd-in-f...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～