666 - PQC 野兽的密文大小？

666 — PQC 怪兽的密文大小？

基于格签名方案的快速指南

因此，我们与 RSA、ECDSA 和 EdDSA 长久告别，并向 ML-DSA（又名 Dilithium — 又名 FIPS 204）、FN-DSA（又名 Falcon — FIPS 206）和 SLH-DSA（又名 SPHINCS+ — FIPS 205）问好。总的来说，ML-DSA 和 FN-DSA 都是基于格的方法，具有不同的实现方法。它们之间的直接对比如下：

• ML-DSA 通常比 FN-DSA 更快（签名和验证速度大约快两倍）。
• FN-DSA 可以从签名中恢复公钥，但 ML-DSA 不能（这在区块链应用中很有用）。
• FN-DSA 具有更小的密钥和密文大小。
• 对于客户端-服务器模型，FN-DSA 将更多的计算负载转移到服务器（这在 IoT 和边缘计算应用中很有用）。

性能和密钥大小

对于 Falcon-512（它具有与 RSA-2048 相当的安全性），我们生成一个 897 字节的公钥、一个 1,281 字节的私钥和一个 690 字节的签名大小，而 FALCON-1024 提供一个 1,793 字节的公钥、一个 2,305 字节的私钥和一个 1,313 字节的签名大小 [ 这里]：

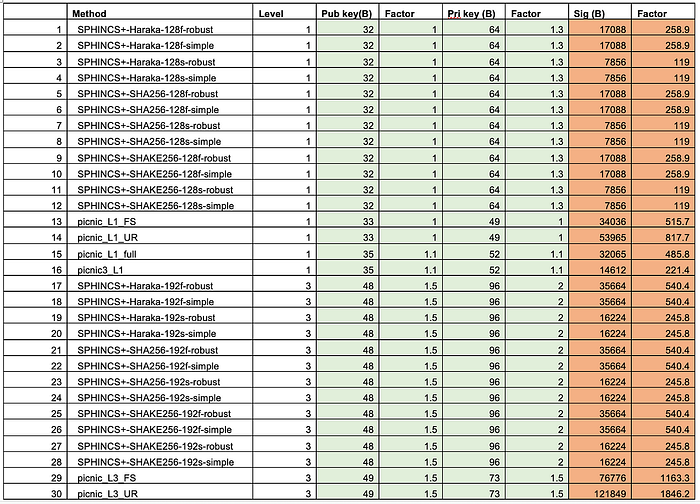
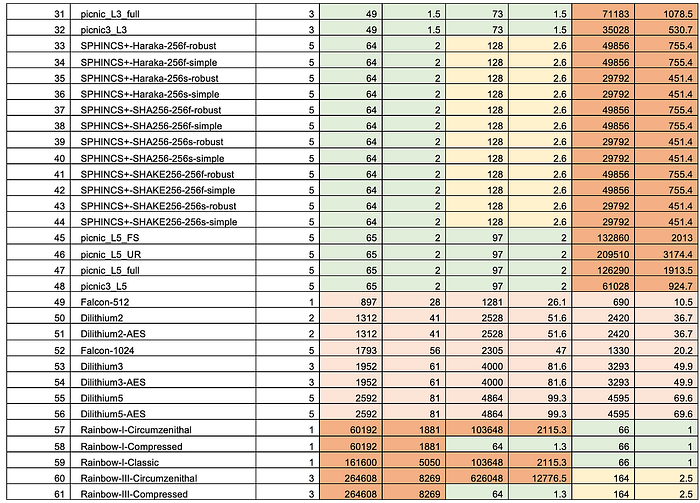
Falcon 使用 NTRU 作为非对称加密方法，并且经过基准测试，其加密速度是 RSA 的两倍，解密速度是 RSA 的三倍。NTRU 是一种不基于因式分解 (RSA)、离散对数或椭圆曲线方法的公钥方法。总的来说，与 Dilithium 相比，它在密钥生成方面相对较慢，但在密钥签名和验证方面性能更接近：

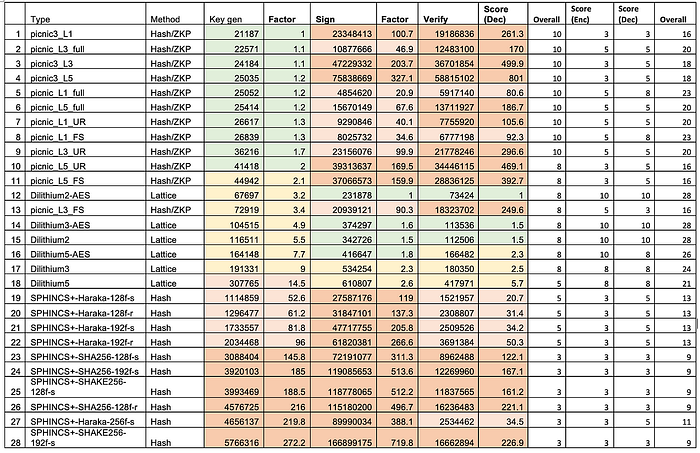
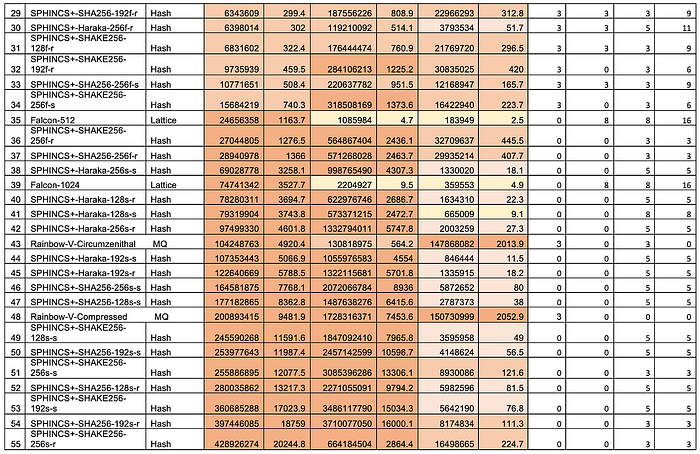
对于 ECDSA、RSA、Ed25519 和 Ed448，我们有：

Method        Public key size (B) Private key size (B)  Signature size (B)  Security level
------------------------------------------------------------------------------------------------------
Ed25519       32                  32                    64                  1 (128-bit) EdDSA
Ed448         57                  57                   112                  3 (192-bit) EdDSA
ECDSA         64                  32                    48                  1 (128-bit) ECDSA
RSA-2048     256                 256                   256                  1 (128-bit) RSA

以下提供了对数字签名 PCQ 方法的分析：

Method                           Public key size    Private key size   Signature size  Security level
------------------------------------------------------------------------------------------------------
Crystals Dilithium 2 (Lattice)        1,312              2,528              2,420         1 (128-bit) Lattice
Crystals Dilithium 3                  1,952              4,000              3,293         3 (192-bit) Lattice
Crystals Dilithium 5                  2,592              4,864              4,595         5 (256-bit) Lattice
Falcon 512 (Lattice)                    897              1,281                690         1 (128-bit) Lattice
Falcon 1024                           1,793              2,305              1,330         5 (256-bit) Lattice
Rainbow Level Ia (Oil-and-Vineger)  161,600            103,648                 66         1 (128-bit) Multivariate (UOV)
Rainbow Level IIIa                  861,400            611,300                164         3 (192-bit) Multivariate (UOV)
Rainbow Level Vc                  1,885,400          1,375,700                204         5 (256-bit) Multivariate (UOV)
Sphincs SHA256-128f Simple               32                 64             17,088         1 (128-bit) Hash-based
Sphincs SHA256-192f Simple               48                 96             35,664         3 (192-bit) Hash-based
Sphincs SHA256-256f Simple               64                128             49,856         5 (256-bit) Hash-based
Picnic 3 Full                            49                 73             71,179         3 (192-bit) Symmetric
GeMSS 128                           352,188                 16                 33         1 (128-bit) Multivariate (HFEv-)
GeMSS 192                         1,237,964                 24                 53         1 (128-bit) Multivariate (HFEv-)

对于 M4 (ARM Cortex-M4 dev) [1] 上的性能，以每秒 CPU 操作次数衡量。请注意，[1] 中未执行 Rainbow 评估，因此 LUOV（一种 Oil-and-Vinegar 方法）已被用于指示性能水平：

Method                           Key generation   Sign   Verify
----------------------------------------------------------------
Crystals Dilithium 2 (Lattice)        36,424     61,312   40,664
Crystals Dilithium 3                  50,752     81,792   55,000
Crystals Dilithium 5                  67,136    104,408   71,472
Falcon 512 (Lattice)                   1,680      2,484      512
Falcon 1024                            1,680      2,452      512
Rainbow Level Ia (Oil-and-Vineger)     2,969      4,720    2,732
Rainbow Level IIIa                     3,216      3,224    1,440
Rainbow Level Vc                       3,736      6,896    4,928
Sphincs SHA256-128f Simple             2,192      2,248    2,544
Sphincs SHA256-192f Simple             3,512      3,640    3,872
Sphincs SHA256-256f Simple             5,600      5,560    5,184

对于 ARM Cortex-M4 设备上的堆栈内存大小 [1]，以字节为单位衡量。请注意，[1] 中未执行 Rainbow 评估，因此 LUOV（一种 Oil-and-Vinegar 方法）已被用于指示性能水平：

Method                           Memory (Bytes)
-------------------------------------------------
Crystals Dilithium 2 (Lattice)        13,948
Crystals Dilithium 3                  13,756
Crystals Dilithium 5                  13,852
Falcon 512 (Lattice)                 117,271
Falcon 1024                          157,207
Rainbow Level Ia (Oil-and-Vineger)   404,920
Rainbow Level IIIa                   405,412
Rainbow Level Vc                     405,730
Sphincs SHA256-128f Simple             4,668
Sphincs SHA256-192f Simple             4,676
Sphincs SHA256-256f Simple             5,084

FN-DSA 方法

因此，让我们看一个 NTRU 如何工作的简单示例。总的来说，Falcon 基于 Gentry、Peikert 和 Vaikuntanathan 方法来生成基于格的签名方案，以及一个陷门采样器 — 快速傅里叶采样。最初，我们选择三个参数：$N$、$p$ 和 $q$。为了生成密钥对，我们选择两个多项式：f 和 g。由此我们计算：

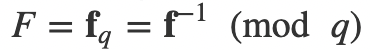
其中 f 和 f _$q$ 是私钥。公钥是：

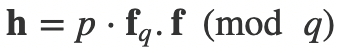
Bob 和 Alice 同意共享 $N$（这限制了最大的多项式幂）、$p$ 和 $q$，然后 Bob 生成两个短多项式（f 和 g），并由此生成他的密钥对。这些多项式的系数为 -1、0 和 1。例如，当 $N$ =11、$p$ =3 且 $q$ =32 时。如果 Bob 选择以下值：

f =[−1,1,1,0,−1,0,1,0,0,1,−1]

那么作为多项式表示：

f =−1+ $x$ + $x²$ − $x$ ⁴+ $x$ ⁶+ $x⁹$ − $x$ ¹⁰

然后选择 g：

g =−1+ $x$ ²+ $x$ ³+ $x$ ⁵− $x$ ⁸− $x$ ¹⁰

然后我们应该能够计算 f 对于 (mod $p$) 和 (mod $q$) 的逆。因此：

f ⋅ f _$p$(mod $p$)=1

f ⋅ f _$q$(mod $q$)=1

使用逆函数，我们得到 [ 这里]：

f _$p$ =[9,5,16,3,15,15,22,19,18,29,5]

f _$p$ =9 $x¹⁰$ +5 $x$ ⁹+16 $x$ ⁸+3 $x$ ⁷+15 $x$ ⁶+15 $x$ ⁵+22 $x$ ⁴+19 $x$ ³+18 $x$ ²+29 $x$ +5

那么公钥变为：

h = $p$ ⋅ f _$q$. f(mod $q$)

在这种情况下，我们得到：

f _$q$ ⋅ g =[−5,−9,−1,−2,11,12,13,3,22,15,16,29,60,19,−2,−7,−36,−40,−50,−18,−30]

为了创建一个环，我们然后除以 $x^{N}-1$ 并得到：

H (Bob's Public Key): [24, 19, 18, 28, 4, 8, 5, 17, 4, 17, 16]

私钥是 f 和 f _$q$。

为了加密，我们取 Bob 的公钥 ($h$)、一个随机多项式 (r) 和一条消息 (M)，然后计算：

$Enc$ = r ⋅ h + M

为了解密，首先我们将 Bob 的私钥 f _$q$ 乘以并取 (mod $q$)：

$Dec$ =( r ⋅ h + M). f(mod $q$)

这会给出：

$Dec$ =( $p$ ⋅ r ⋅ f _$q$ ⋅ g + M). f(mod $q$)

由于 (f _$q$. f)(mod $q$) 是 1，我们得到：

$Dec$ =( $p$ ⋅ r ⋅ g + M ⋅ f)

最后，我们将 f _$p$(mod $p$) 乘以：

$Dec$ =( $p$ ⋅ r ⋅ g + M ⋅ f). f _$p$(mod $p$)

这将是：

$Dec$ = $p$ ⋅ r ⋅ f ⋅ f $p$ + M ⋅ f ⋅ f $p$(mod $p$)

由于我们有一个 $p$ 的乘数，我们将得到第一个项的零值，因为我们有 (mod $p$) 操作：

$Dec$ =0+ M ⋅ f ⋅ f _$p$(mod $p$)

由于 f ⋅ f _$p$(mod $p$) 将是 1，我们得到：

$Dec$ = M

参数的示例值是：

• 最小安全性：$N$ =167、$p$ =3、$q$ =128。
• 良好安全性：$N$ =251、$p$ =3、$q$ =128。
• 强安全性：$N$ =347、$p$ =3、$q$ =128。
• 卓越安全性：$N$ =503、$p$ =3、$q$ =256。

编码

一系列方法都在这里。总的来说，JavaScript 允许代码在浏览器中运行。

使用 JavaScript 的 NIST FIPS 206 (FN-DSA)

我们可以使用多种环度大小来实现 NTRU 方法 [ 这里]：

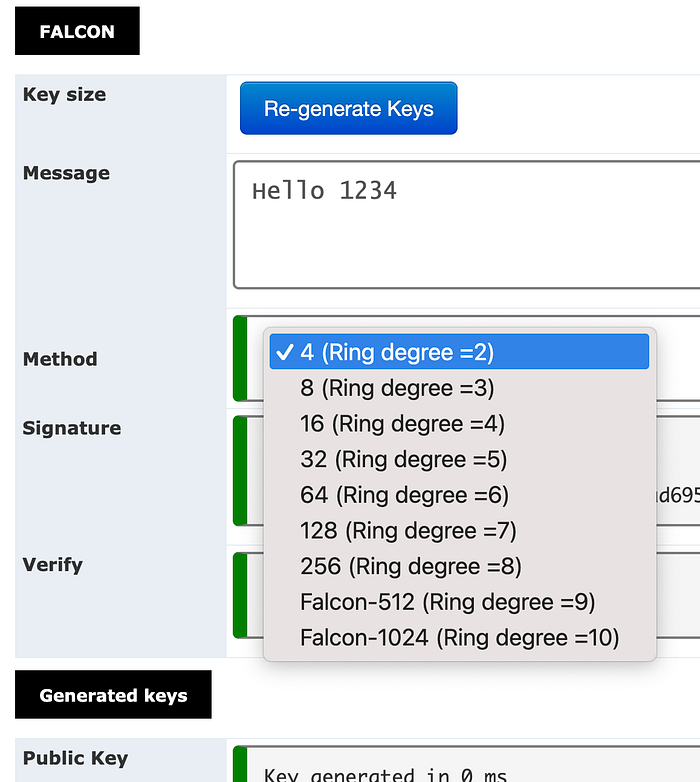
总的来说，我们需要 Falcon-512 的环度为 9，公钥为 1,281 字节，私钥为 897 字节：

然后我们可以实现签名 [ 这里]：

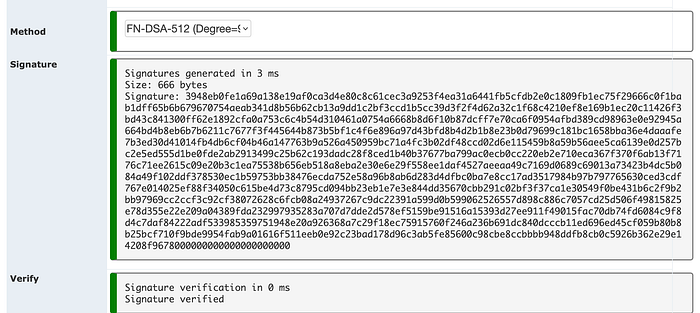
我们可以看到签名和验证相当快，并且密文是 666 字节。

结论

Falcon 在性能上比 Dilithium 慢，但密钥大小和密文要小得多：

Method                           Public key size    Private key size   Signature size  Security level
------------------------------------------------------------------------------------------------------
Crystals Dilithium 2 (Lattice)  1,312            2,528              2,420         1 (128-bit) Lattice
Falcon 512 (Lattice)            897              1,281                666         1 (128-bit) Lattice

参考文献

[1] Kannwischer, M. J., Rijneveld, J., Schwabe, P., & Stoffelen, K. (2019). pqm4: Testing and Benchmarking NIST PQC on ARM Cortex-M4

• 原文链接： medium.com/asecuritysite...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～