各后量子密码学算法安全性评估

在发布了我的关于 UOV 的系列文章后，我收到的一个反馈是，我的博客文章让人们对该方案的安全性更有信心，因为“至少有人在研究这些东西”。我并不一定知道这是我从我的文章中得出的结论，但它给了我一个想法，写下我对 PQC 中各种方法和问题族的安全性，非常主观且带有偏见的估计。

由于我没有无限的智慧或时间旅行的天赋，这些充其量只是有根据的猜测，我对其中的任何错误不承担任何责任。

概论

密码学中有一句颇为流行的说法“攻击只会变得更好”。这是一个空洞的真命题，因为很明显，攻击者总是会使用目前已知的最强大的技术，但我认为它至少在某种程度上具有误导性，暗示攻击方面的进展不仅是不可避免的，而且在某种程度上是持续的。

相反，我们通常看到的是这样的情况：最初，当某种技术第一次被认真讨论时，攻击会迅速出现，并且必须调整参数以应对这些攻击。随着时间的推移，随着我们对该领域的理解不断加深，我们倾向于改进这些攻击，但这是一个收益递减的过程。有可能某种新颖的数学技术会引发攻击方面的新一轮快速进展，但重要的是，攻击通常不会持续改进。

例如，如果我们看看 RSA，我们首先有朴素的因式分解算法，例如试除法和费马方法，它们早于密码学的使用。然后，在 70 年代，它们加入了该领域的第一个重大改进，Pollard 的 rho 算法。在 80 年代，我们得到了二次筛法，作为第一个亚指数算法，以及各种格方法。最后，在 90 年代，也就是 30 多年前，我们得到了当前最佳的因式分解算法，即一般数域筛法，它是二次筛法的改进，以及格技术的进一步改进。量子算法也首次出现在舞台上，即 Shor 算法。此后，成功案例大幅减少，主要局限于对一般数域筛法的相对较小的改进。

这并不是因为我们停止了对因式分解算法的研究，而是大部分精力转移到了其他目标上，例如 Montes 算法，用于在离散赋值环上分解多项式。

如果我们看看椭圆曲线，攻击的故事就更不令人兴奋了。迄今为止，还没有已知的针对椭圆曲线的通用经典攻击，其效果优于时空权衡的暴力搜索版本。这同样不是因为该主题没有被研究，椭圆曲线是代数几何最基本的构建块之一，我们对它们非常了解。事实上，我们对它们的了解非常深入，甚至可以开始解释这种缺乏攻击的情况：它们是目前最通用的 Diffie-Hellman 形式。

总而言之，这使得我们预测哪种算法可能被破解以及哪种算法可能持续存在的工作变得非常非常困难。我们看到的不是好的、可预测的趋势，而是主要看到的是一个每隔几十年就会发生巨大飞跃的过程。

看待相同趋势的另一种不同视角是，每次一个方案在攻击中幸存下来，它就会变得更值得信赖。从这个角度来看，失败的攻击教会了我们关于方案本身的一些东西，调整了我们的先验认知，使其更值得信赖。对于告诉我们关于底层问题的 fundamental 知识的攻击来说，尤其如此； 攻击越普遍，它就越能教会我们为什么一个方案具有弹性。

但是，现在，不再赘述，以下是我个人认为各种 PQC 方法有多安全的列表，以及我个人对该领域的熟悉程度以及我认为该领域被研究的程度。

第一名：基于哈希的签名

关于基于哈希的签名，没有什么可说的。它们具有对所用哈希函数性质的安全归约。任何签名方案，以及几乎任何公钥加密方案，都需要在其构造中使用哈希函数，无论是用于压缩消息、充当随机预言机、密钥派生函数还是单向函数。如果我们无法构造安全的哈希函数，我们就无法进行密码学。事实上，如果我们一直无法创建安全的哈希函数，我们很可能生活在一个 P 等于 NP 的宇宙中。

基于哈希的签名方案具有归约证明，将其安全性归约到其底层哈希函数的安全性。因此，基于哈希的签名方案至少与任何其他非对称（或对称）密码原语一样安全。它们有很多缺点，但缺乏安全性不是其中之一。虽然我没有对它们进行深入研究，但也确实没有什么可说的关于它们的安全性。它们是安全的。

请注意，某些基于哈希的签名方案的一个缺点是需要保持状态 (LMS/XMSS)。虽然如果使用得当，这些方案与其哈希函数一样安全，但如果状态管理不正确，即一次性签名被多次使用，则情况并非如此。虽然我对基于哈希的签名的数学原理有极高的信心，但我对我们集体偶尔不破坏状态的能力也极度缺乏信心。

第二名：格（Lattices）

很难过分强调我对格的信心。通用格（例如 FrodoKEM 中使用的格）被破解几乎等同于证明 P = NP，届时所有密码学都将消失（因为对称密码学很容易归约到布尔可满足性），并且是时候寻找另一份职业了。

格在算术数论中占有重要地位，因为它们在研究数域时自然而然地出现。因此，格算法实际上比因子分解算法更重要。高效的格归约算法解决的问题数量远远多于高效的因子分解算法。主要原因是格问题是丢番图方程问题最简单的形式，即线性丢番图方程。你可以在我的其中一篇之前的博客文章中看到一个例子。这使得格归约成为用于计算离散数学中几乎任何内容的最有用的算法之一。

它们不仅限于代数数论，还出现在代数几何中，用于描述复数上的阿贝尔簇。或者，正如我的博士论文所研究的那样，p-adic 数。鉴于它们在数学中的核心地位，如果有人以某种方式找到一种改进通用格归约的方法，我会感到非常惊讶。即使在量子算法方面，格归约也可能是被研究得最多的算法之一，到目前为止，尚未发现任何通用改进，并且已经确定了几个看起来很 fundamental 的障碍。

格作为一种数学对象，已经被研究了与椭圆曲线几乎相同的时间，因为两者都来自关于椭圆周长的相同底层问题。在这项研究中，某些积分自然而然地出现，定义了一个在复平面中具有两个周期的函数。换句话说，可以看作是在模格的复数上定义的函数。而其中最简单的函数 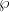，服从一个微分方程 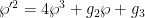。换句话说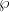， 及其导数定义了一条椭圆曲线。

在密码学中，格也已经被研究了与椭圆曲线几乎相同的时间。首先作为一种攻击，因为它们具有解决丢番图方程的能力，然后很快就成为密码系统本身，通过增加格的秩，使其归约变得无法计算。你之前可能没有听说过它们的主要原因是，与椭圆曲线和 RSA 相比，它们的开销通常更大，这使得它们在一个椭圆曲线和 RSA 未被破解的世界中缺乏吸引力。

但我们没有使用通用格，我们专门使用模块格。这些格来自数域序。数域是 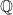的域扩张（例如将虚数单位 i 添加到有理数），而这样一个数域中的序是对整数的推广（例如将虚数单位 i 添加到整数，以获得称为 高斯整数的数域序）。这些数域序本身就是规范格，并且任何在其上的有限生成模块（即向量空间，但对于环）也是以规范方式的格。

如果 ML-KEM 或 ML-DSA 被破解，我会把钱压在利用这种额外结构上。然而，即使对于这种额外的结构，它也得到了很好的理解和研究。

具体来说，看看 MLWE 和 NTRU，这两个问题都与 p 进有理重构问题密切相关。在 MLWE 的情况下，我们需要切换到 RLWE，但一个数域序可以看作是某个子域的序的模块，所以这并没有真正改变局面。

那么什么是 rational 重构问题？回想一下，为了攻击 LWE，我们需要找到 $s, e$，使得 $As + e = t \, \text{mod} \, q$，这主要归结为描述核，即 $As + e = 0\, \text{mod} \,q$ 的解。对于 RLWE（或者实际上是 NTRU），我们需要切换到一个数域序，我们主要通过用小写 $a$ 替换大写 $A$ 来实现。当然，我们可以在没有太多后果的情况下改变误差项的符号，并为我们需要减少的格写出 $as - e = 0 \, \text{mod} \, q$。稍微重新排序一下，这相当于 $a = e/s \, \text{mod} \, q$。由于 $e$ 和 $s$ 在某种度量中都很小，这意味着我们要求的是，给定一个具有有界分子和分母的分数，它只在模某个理想（或更一般地说是 有限位置）的情况下已知，找到分子和分母。

当我们用无限位置替换有限位置时，我们都知道这个问题，尤其是在 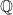上，尽管通常不太正式地穿着数学术语：这是哪个分数最适合给定的有限精度十进制展开的问题，例如 1.666 的输出是否来自 5/3 的实际结果，或者 1666/1000。

这个问题（在有限位置上，即模一个素数）在研究数域时相对自然地出现，而我们知道的解决它的唯一方法是格归约。

这是算术数论中一个非常常见的模式，你通常会遇到其中出现的问题并重新表述它们，直到你可以将它们表达为格问题，然后在数域足够小时继续减少格。另一方面，你可以使用数域的数论性质来说明关于格的一些信息而不减少它的情况非常罕见。

话虽如此，在格密码方面，我们并没有使用随机数域，而是一组相当小的非常具体的数域，它们具有通常在许多数域中不会遇到的性质，例如具有 1 的类数，以及一个易于计算的单位群（直到一些易于计算的有限辅因子，也就是说，但这通常对于随机数域来说是一个困难的格问题，但对于我们用于密码目的的在 2 上高度分歧的循环域来说却很容易）。

话虽如此，即使存在这些瑕疵，当谈到模块格密码时，我们谈论的是数学中一个非常非常被很好理解和探索的部分，应该可以非常安全地用于密码目的。

第三名：码（Codes）

我对码的了解比我对格的了解要少得多，我一直认为它们是格的较小的兄弟姐妹。这两种方案从根本上都是通过欠定的线性系统工作的，其中解具有某些特殊的性质。在格的情况下是小，在码的情况下是有很多零（即在汉明度量中是小的）。它们的构造有很多相似之处，以至于基于码的密码可以使用与格密码必须处理的相同的格归约技术进行攻击。与格相比，码在数学中的核心地位要低得多，但这到底是好事还是坏事很难说。但实际上，我没有对码进行任何必要的深入研究，以对它们发表太多意见，只是认为它们没问题，可能至少只要网格没问题即可。而且，它们在几乎所有实例化中的效率都低于网格，并且至少我不知道如何将它们视为更普遍的数学问题（类似于支配 MLWE/NTRU 的 p 进有理重构问题）。

第四名：同源（Isogenies）

现在到了一个有点争议的位置：同源。什么，即使 SIKE 被破解了？是的，好吧，很明显我没有把 SIKE 放在第四位，它略低于第四位，就在 Vigenère 密码之上，只是因为攻击更有趣。

另一方面，SQISign 是另一回事。在我看来，将其稍微高于多元密码的主要原因是，我们更好地理解了底层的难题以及它与方案本身的关系。

我不羞于承认我偏爱漂亮的数学，而 SQISign 做了一些我所知道的最美丽的数学。话虽如此，该方案目前速度太慢以至于无法在实践中使用，虽然它可以归约到自同态问题，但我们目前无法排除自同态问题最终变得容易，特别是考虑到它在数学中的核心地位远不如格。但是，它已经得到了一定程度的广泛研究，但我有点担心代数几何中自同态问题的最佳专家现在甚至才慢慢开始了解基于同源密码的存在。毕竟，SIKE 攻击基于 1997 年发现的一个定理，直到 2022 年才被发现，这表明学术代数/算术几何与从事基于同源密码的密码学家之间存在巨大差距。

第五名：多元密码( Multivariate Cryptography)

我已经写了关于非平衡油和醋的整个 系列，这可能是多元方案中最基本的方案。从那以后，出现了一种新的攻击，利用楔积。虽然这种攻击远非灾难性的，但它也感觉非常随意，类似于 Kipnis-Shamir 对平衡油和醋的攻击，在我看来，我们缺少一些东西来真正充分理解这个空间。

有趣的是，甚至在论文发表之前，我就曾尝试使用楔积来攻击 UOV，但没有成功，更准确地说，我试图弄清楚余切空间中是否存在可以利用的结构，因此事实上，楔积是一个有意义的攻击向量，这本身并不令人惊讶，但是，如果我们想信任 UOV，我们必须在我看来更好地理解这里的难题实际上是什么。

很容易在这里指向 Gröbner 基，但在我看来，从通用 Gröbner 基计算到特定 UOV 问题的差距相当大。虽然所有 NP 完全问题都必然相互归约，但归约到 Gröbner 基计算是最容易的归约之一，就像你可以通过字面上翻译指令将计算机程序归约到布尔电路可满足性问题一样，你可以将关于多项式的问题归约到 Gröbner 基计算。

关于多元密码学，有一件事特别让我印象深刻，那就是试图减小公钥大小的变体最终经常被破解。对我来说，缺少一些关于充分理解是什么让这个问题难以充分信任的东西，但我更好地理解问题空间的进展至少让我瞥见了为什么基本的 UOV 应该是安全的。

话虽如此，实际上，我应该将它们放在同源之上，主要是因为我们在这个领域经历了更多的幸存攻击，但这是我的列表，如果它不包含至少一个令人不安的位置，那么它现在就不会非常主观了，不是吗？

为什么 RSA 和椭圆曲线会一起崩溃

我最近被问到的一个问题是，为什么 RSA 和椭圆曲线虽然看起来如此不同的密码系统，但都容易受到 Shor 攻击的影响，而所有其他方案几乎没有提到 Shor 为什么不适用于它们。虽然乍一看，RSA 和椭圆曲线确实看起来非常不同，但它们实际上比人们想象的要相关得多，其中一些甚至在经典攻击中已经可见。

正如我在我关于为什么椭圆曲线实际上是离散对数问题的唯一选择的文章中所描述的那样，椭圆曲线包含乘法离散对数作为子情况（至少如果你允许稳定模型）。并且对于乘法离散数问题，我们已经有相同的攻击适用于 RSA 和 DLOG。从这个角度来看，在 RSA 上呈多项式式的攻击也解决了 ECC 可能不那么令人惊讶。

更具体地说，Shor 算法实际解决的是阿贝尔隐藏子群问题：给定一个群 $G$，一个函数 $f \colon G \to X$ 被称为隐藏 $G$ 的子群 $H$，如果 $f$ 在每个陪集上都是常数，但对于不同的陪集则不同。特别是，如果 $H$ 是一个正规子群，这意味着 $f$ 在 $G/H$ 上是定义明确的且单射的。如果所讨论的群是阿贝尔群，则隐藏子群问题是阿贝尔问题。这有点拗口，所以让我们首先看一个简单的例子，使用 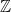作为我们的群，并尝试隐藏 $3\mathbb{Z}$ 作为一个子群。如果一个函数在陪集上具有不同的值，它将隐藏这个子群，例如，如果该函数只是整数模 3 的值。对于一个稍微有趣的函数，它实际上有意义地隐藏了一些东西，我们可以看看变体的 Sudoko 世界，在那里我们经常看到模块化线或模块化镜像或类似的概念，这需要某些数字具有相同的余数模 3（例如这个或那个）。解决这些难题通常是通过将相应的数字着色为三种颜色之一来完成的，指示余数类模 3。重要的是，（至少最初）不知道哪种颜色对应于哪个余数类，这开始表明为什么该函数被认为隐藏了这个子群。当然，即使你只是将整数映射到颜色，隐藏的子群对于任何可以数到三的人来说仍然非常容易找到（而且重要的是，解决 Sudoko 与解决隐藏子群问题无关），但你可以想象对于一个更大的模数，这会变成一个实际的难题。

虽然不是必需的，但在查看阿贝尔群的这个问题时，了解阿贝尔群的分类问题非常有用。所有有限生成的阿贝尔群都可以写成乘积 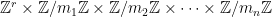，其中 $m_1 | m_2 | \dots | m_n$。知道这一点意味着我们非常清楚，至少在理论上，阿贝尔群的任何子群看起来像什么，这将使接下来的几个部分更容易掌握其通用性。

知道 Shor 算法可以解决阿贝尔隐藏子群问题，并且现在知道阿贝尔隐藏子群问题是什么，剩下的就是显示子群在哪里隐藏，对于 RSA 和椭圆曲线都是如此。如前所述，椭圆曲线或多或少是所有 DLOG 群中最通用的，因此我们无需担心椭圆曲线如何工作的内在机制，而可以只采用一个通用群 G（作为奖励，这允许我使用乘法表示法而不感到肮脏）。实际上，让我们从 DLOG 开始。

因此，给定两个元素 $a, b \in G$，我们正在寻找 $k$，使得 $a^k = b$。我们不是使用 G 作为域，而是使用两个 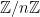的副本，并将我们的函数 $f \mathbb{Z}/n\mathbb{Z} \times \mathbb{Z}/n\mathbb{Z} \to G$ 定义为 $(m_1, m_2) \mapsto a^{m_1}b^{-m_2}$。由于 $b=a^k$，这等于 $(m_1, m_2) \mapsto a^{m_1-k\cdot m_2}$，即它是 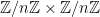上的线性变换，后跟一个离散指数。

但是，离散指数是一个群同构，因此我们可以从根本上忽略它，因为隐藏群的定义从一开始就不太关心函数的范围。作为一个线性函数，很容易看到 $f$ 映射到单位的位置，即精确地映射到由 $(k, 1)$ 生成的向量。 由于 $f$ 是一个群同态，我们可以使用群同构定理来了解 $f$ 在每个陪集上都是常数，并且在商上是单射的，即 $f$ 隐藏了一个阿贝尔子群。应用 Shor 算法，并获得这个子群的生成器，我们可以恢复 $k$，因为这个子群的所有元素都具有 $(k\cdot m, m)$ 的形式。

将 RSA 重新表述为阿贝尔隐藏子群问题甚至更容易：RSA 的安全性建立在攻击者不知道群的阶上，因为 $\left(\mathbb{Z}/n\mathbb{Z}\right)^\times$ 的阶是 $\varphi(n) = (p-1)(q-1)$，由此我们可以轻松恢复 $n$ 的因子 $p$ 和 $q$。那么如何使阶查找成为阿贝尔隐藏子群问题？只需取一个随机元素 $a\in \left(\mathbb{Z}/n\mathbb{Z}\right)^\times$ 并定义 $f$ 为 $f \colon \mathbb{Z} \to \left(\mathbb{Z}/n\mathbb{Z}\right)^\times\;;\;x\mapsto a^x$。这个函数对于 $a$ 的阶的所有倍数具有相同的结果，换句话说，它隐藏了 $ord(a)\mathbb{Z}$ 作为 $\mathbb{Z}$ 的子群。并且一个元素的阶始终是一个群的阶的除数，因此我们可以使用它来查找 $n$ 的因子。

隐藏子群问题比这更通用，并且大多只是一个重新陈述问题的框架。实际上，我们可以将格归约重新表述为隐藏二面体子群问题。但重要的是，量子计算机真的很擅长在阿贝尔群上运行，但至少到目前为止，尚未在非阿贝尔群上表现出任何成功。鉴于它们的构造，这确实是有道理的，并为我们提供了一些关于为什么到目前为止格已经承受住了量子密码分析攻击的数据。

• 原文链接： keymaterial.net/2025/12/...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～