从签名中重构公钥

我一个奇怪的爱好是研究密码方案的合理属性，这些属性是没人承诺过有或没有的。无论是隐形火蜥蜴还是通过共享秘密进行绑定，任何不仅仅是无聊的 IND-CCA2 或存在不可伪造性的东西，都是构建漏洞的绝佳材料。

通常，对于签名方案，你有公钥，并且想知道给定的签名是否有效。但是，如果我们有消息和签名，假设签名有效，并且想知道哪个公钥签署了它呢？如果你想攻击某些提议的“每个人都只使用密码签名来进行所有操作”方案中的匿名性，这是一个相当令人愉快的属性。

第一章: ECDSA

这个非常有名，它甚至有自己的 维基百科章节。简而言之，是的，完全有可能从单个有效签名中恢复公钥。

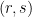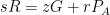ECDSA 签名是两个整数 使得 ，其中 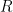是 x 坐标为 的两个点之一。为了重构公钥，我们可以直接求解 并得到 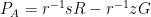，其中我们将 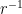计算为 模椭圆曲线阶的逆。

公钥已恢复。

第二章: RSA

这里，它变得有点棘手。我们需要两个签名，而不是一个签名，即 $s_1$ 和 $s_2$，以及相应的消息 $m_1$ 和 $m_2$。RSA 通常会哈希消息，然后以某种方式填充它，但我们并不真正关心这里的部分，并假设 $m$ 已经是这个哈希和填充的消息。唯一重要的属性是，为了有效，RSA 签名必须满足 $s^e = m \mod n$。为了实现这个属性，签名者已经计算了 $s = m^d \mod n$，其中 $d\cdot e \mod \varphi(n)$。$e$ 通常是 65537，我们将只假设这个值并只恢复 $n$。我们通过计算 $n' = \gcd(s_1^e - m_1, s_2^e - m_2)$ 来做到这一点。请注意缺少模运算，这只是一个原始指数，是的，结果将具有大约 65537 倍于签名、消息或模数的位数。欧几里得算法非常高效，它不在乎。好吧，它有点在乎，但我仍然能够在几分钟内计算出 2048 位的公钥。然而，结果并不完全等于 $n$，因为有 1/4 的概率这两个数都是偶数，并且有 1/9 的概率它们都可以被 3 整除。但是 $n$ 应该只有两个非常大的素数因子，所以在对前几百个素数进行试除后，我们可以相对确定剩下的就是实际的公钥。

第三章: 稍微绕道到 Schnorr 签名

在我们进入后量子签名方案之前，我们应该再看一个经典签名方案，虽然在实践中用得不多（诅咒你，专利），但对于理解 PQ 方案来说非常重要。Schnorr 签名是椭圆曲线签名，它使用一种特定的方法将零知识证明转换为签名方案，即 Fiat-Shamir 转换。

对于 Schnorr，我们有通常的设置，即阶数为 $n$ 且生成点为 $G$ 的椭圆曲线，以及公钥 $P_A = x_AG$。

零知识协议的工作方式如下：

首先，证明者提交某个值 $R$。在 Schnorr 的情况下，这是通过选择一个随机值 $k$ 并设置 $R = kG$ 来完成的。

接下来，验证者发出一个挑战 $c$。

证明者现在揭示 $s = k - c\cdot x_A \mod n$。验证者可以检查 $R = sG + cP_A$。

这证明了证明者知道 $x_A$，因为如果事先不知道挑战，则在不知道它的情况下无法给出给定承诺的证明 $s$（或者手头有一台量子计算机）。然而，这个证明是零知识的，因为如果事先知道挑战，那么想出正确的承诺和证明是相当容易的，同时仍然保持承诺均匀随机，通过随机选择 $s$，然后计算 $R' = sG$，并“承诺”到 $R = R' + cP_A$。这意味着我们多次玩这个游戏不会失去安全性，攻击者不妨专注于密钥恢复攻击。

为了将这个零知识协议转换为签名方案，我们将挑战者替换为哈希函数。为了确保我们的承诺实际上被提交了，我们也将其添加到哈希函数中。换句话说，签名方案看起来像这样：

随机选择 $k$。将 $r$ 设置为 $R = kG$ 的 x 坐标。计算 $c = H(r || m)$，并设置 $s = k - c\cdot x_A$。我们现在有两种变体，要么将签名设置为元组 $(r, s)$，要么设置为元组 $(c, s)$。

在第一种情况下，验证者计算 $c = H(r || m)$ 并检查 $sG + cP_A$ 的 x 坐标是否为 $r$，在第二种变体中，验证者首先计算 $sG + cP_A$，取 x 坐标并检查 $c = H(r || m)$。

两种变体都是完全安全的，并且在椭圆曲线的情况下，选择哪一个真的没有关系。但现在它变得有趣了：我们是否可以恢复公钥取决于变体。如果签名是 $(r, s)$，我们可以计算 $c = H(r || m)$ 并执行与之前在 ECDSA 上相同的操作，并计算 $P_A = c^{-1}R - c^{-1}sG$。但是，如果签名是 $(c, s)$，我们没有办法找到 $r$，因为它是具有足够熵的随机 x 坐标，以至于不可能找到 $c$ 的原像。

第四章: Dilithium

有了这个，我们进入我们的第一个后量子签名方案。Dilithium 真的应该有自己的完整博客文章，但由于在这里我们只对恢复公钥感兴趣，我们可以简化它很多。回想一下，对于一个带错误的学习方案，公钥是一个向量 $t$ 和一个矩阵 $A$ 模某个素数 $q$，使得 $t = As + e \mod q$，其中有一些 短 向量 $s$ 和 $e$。密钥是 短 向量 $s$。对于 Dilithium，我们现在使用以下零知识证明：

首先，证明者提交 $Ay$ 的高位 $w_1$，其中 $y$ 是相对较短的。仅使用高位类似于添加错误，因为小错误也只影响最低有效位。然后，挑战者用一个小标量 $\mathit{c}$ 进行挑战（这个标量以某种方式是多维的，我在这里会简单地忽略它），证明者用 $z = y + \mathit{c} s$ 回应。现在，挑战者可以检查 $Az - \mathit{c} t = Ay + \mathit{c}As - \mathit{c}As - \mathit{c}e$ 是否与承诺 $w_1$ 具有相同的高位。

我们将忽略这个协议不是零知识的，并且 Dilithium 实际上必须使用一种叫做 Fiat-Shamir with aborts 的东西，因为，如前所述，这些东西真的应该进入它自己的博客文章。

对于我们的目的，唯一重要的问题是如何将这个零一些知识证明转化为签名方案。对于我们恢复公钥的雄心来说，坏消息来了：事实证明，承诺 $w_1$ 明显大于挑战 $\mathit{c}$，因此 Dilithium 在签名中使用了挑战，落在了 $(\mathit{c}, z)$ 上，而不是承诺，就像 Schnorr 签名一样，这使得公钥无法恢复。

一个单独的、有趣的问题是，如果 $w_1$ 是签名的一部分，我们是否可以恢复公钥。如果我们知道 $A$，我们可以至少恢复 $t$ 的高位，它们是重要的那些。（事实证明，Dilithium 实际上甚至没有在实际公钥中包含 $t$ 的最低有效位，以节省其中的一些位）。

在不知道 $A$ 的情况下，这变成了大量的线性代数，我没有做过，你肯定需要不止一个有效的签名，因为单个签名不包含足够的信息来恢复那个巨大的矩阵。

我没有做那线性代数的部分原因是，如果我们通过某种侧信道或类似的方式知道 $w_1$，我们仍然没有机会恢复公钥，因为 Dilithium 粗鲁地在计算挑战时将公钥与消息哈希在一起，破坏了任何恢复的希望。

第五章 SPHINCS+

这很好地将我们带到了 SPHINCS+。SPHINCS+ 是一种基于哈希的签名方案，这意味着它遵循简单的逻辑，即如果在创建公钥时，你已经知道你想要签名什么，你可以只哈希该东西并将其称为你的公钥。如果你想签名很多东西，你可以将所有这些东西打包成一个 Merkle 树，并声明该树的根是你的公钥。如果你不知道你想签名什么，你可以通过为哈希的单个位创建承诺来承诺每个可能的消息。在那里扔一些随机性，这样你就不会意外地重用你的承诺到打破的程度，你就得到了 SPHINCS+。该方案可能也应该有自己的博客文章，但我们现在真的不需要更多了。Merkle 树包含证明会泄露 Merkle 树的根节点，只要我们可以观察到证明包含的初始消息。不幸的是，由于非常喜欢哈希，SPHINCS+ 的作者做了与 Dilithium 相同的事情，并在计算初始消息哈希时哈希了公钥，使得公钥无法恢复。你只需要相对较少的额外信息即可恢复，并且可能通过对验证逻辑进行一些时序攻击就足以捡起来并沿着 Merkle 树继续前进。

第六章：非平衡油醋

最后，让我们看看第二个入门中一个有趣的候选者，称为非平衡油醋(Unbalanced Oil and Vinegar)。它再次可以使用自己的博客文章，但它在这里被稍微浓缩，并省略了诸如私钥是什么以及任何人实际上如何首先计算有效签名等不必要的细节。

还记得在高中时解二次方程吗？就像给出一个值 $y$，找到值 $x$，使得 $ax^2 + bx + c = y$？现在想象有人将其变成签名方案。当然，即使是对手也知道 $x_{1,2} = \frac{-b\pm \sqrt{b^2 - 4ac}}{2a}$，因此我们将不得不通过使事情更高维来稍微增加难度，但这个想法仍然相同。

UOV 公钥是一个由 $o$ 个变量组成的 $o + v$ 个变量的 $o$ 个二次方程 $(f_i(x_1, x2, \dots, x{o+v})_{i=1,\dots o}$ 系统。这些方程是齐次的，因此我们也可以通过矩阵来描述它们：$f_i(x) = x^TA_ix$，其中 $x$ 是一个向量。为了用它进行签名，签名者计算（通过一个奇迹般的陷门，这篇文章太短以至于无法包含）一个值 $x$，使得 $(f_i(x))_i={1\dots o} = H(m)$。UOV 的真正技巧在于签名者如何计算此原像的过程，但我们不关心这一点，我们关心的是恢复公钥。显然，由于 UOV 签名比 UOV 公钥短得多，因此单个签名不足以恢复公钥，但是如果我们收集的不仅仅是一个呢？我们拥有一组未知的多项式，在某些已知的点（签名）上进行评估，得到某些已知的图像（消息的哈希值）。这听起来像是多项式插值的工作！

实际上，只需 $\frac{(o+v)(o+v+1)}{2}$ 个消息/签名对，我们就可以恢复公钥：

我们采用基

$\left(bi\right){i=1}^{\frac{(o+v)(o+v+1)}{2}}=\left(X_i\cdot Xj\right){i=1,j=i}^{u+v, u+v}$ 并且对于每个消息/签名对 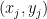，我们计算 $b_k(x_j)$。由于我们知道 $f_i(x_j)=y_j$，并且知道每个 $f_i$ 都是 $b_k$ 的线性组合，这给了我们一个线性方程，一旦我们收集了 $\frac{(o+v)(o+v+1)}{2}$ 个签名，它就开始具有唯一的解。最重要的是，UOV 不会哈希公钥（可能是因为公钥非常庞大），因此即使在已发布的候选版本上，此方法也有效。

UOV 还具有一个具有压缩公钥的版本（如前所述，公钥有点大）。这篇博客文章已经很长了，所以我只想说我们无法恢复此压缩公钥，因为它涉及一个种子，并且当原像具有如此大的熵时，我们无法找到哈希函数的原像。但是扩展的公钥在任何方面都是等效的，因此我仍然将 UOV 视为成功。

结论

公钥是公开的，即使你不告诉人们关于它们。签名方案在密钥恢复的容易程度上差异很大，但请记住，验证逻辑通常不是为了抗侧信道攻击而编写的，因此即使对于不以代数方式泄漏公钥的方案，攻击者可能仍然有一种方法来恢复公钥，并且你需要设计你的协议以抵抗该属性。

• 原文链接： keymaterial.net/2024/06/...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～