2¹³⁰−5之美以及使ChaCha20更快

2¹³⁰−5 的美妙之处以及使 ChaCha20 更快

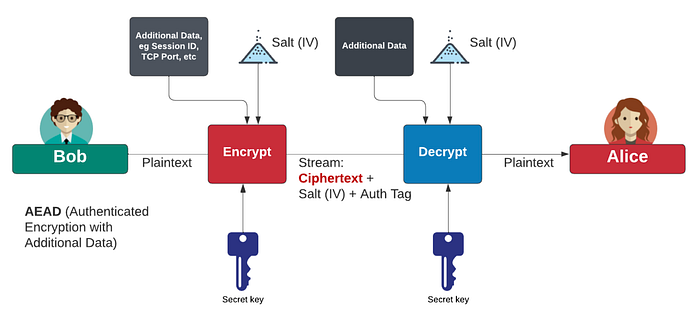
强大的 Daniel J Beirnstein 喜欢用舞蹈来命名加密方法，包括 Rumba、Salsa 和 ChaCha。由于这些是流密码，我们需要一个 MAC（消息认证码）来检查这些位是否被翻转。为此，他使用了 Poly1305，它使用素数 2¹³⁰−5 进行计算（它非常高效且足够大以保证安全）。这个数字在使用 32 位和 64 位架构时也很高效，因此有助于支持各种设备。

2¹³⁰−5 的美妙之处

当我们观察 2¹³⁰−5 时，我们发现很多位都被设置为 1：

>>> 2**130-5
1361129467683753853853498429727072845819
>>> hex(2**130-5)
'0x3fffffffffffffffffffffffffffffffb'
>>> bin(2**130-5)
'0b1111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111011'
>>>
>>> bin(2**130)
'0b10000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000'

当我们乘以 2¹³⁰ 时，由于 1 的存在，它会非常高效，最终我们只需要进行位移和加法运算。对于值 5，乘法运算如下：

5x=4x+x=(x≪2)+x

因此，我们只需将位向左旋转两位并加上 x。

减少轮数

对于 ChaCha20，我们有 20 轮加密，每一轮都使其更难以破解。但是，许多人担心对于许多系统所需的安全性级别来说，20 轮太多了。为此，我们可以将轮数减少到 12 轮，从而提高性能（这对于容量有限的设备尤其有用）。人们也认为，ChaCha12 至少提供了与 AES-256 相当的安全性级别。

以下代码使用 Zig Version 0.15.1 编译 [ 这里], 并集成了 ChaCha12 [ 这里]：

const std = @import("std");
const aead = @import("std").crypto.aead;

pub fn main() !void {
    var gpa = std.heap.GeneralPurposeAllocator(.{}){};
    defer _ = gpa.deinit();
    const allocator = gpa.allocator();
    var stdout_buffer: [4096]u8 = undefined;
    var stdout_writer = std.fs.File.stdout().writer(&stdout_buffer);
    const stdout = &stdout_writer.interface;
    // Get the command-line arguments
    var m: []const u8 = undefined;
    const args = try std.process.argsAlloc(std.heap.page_allocator);
    defer std.process.argsFree(std.heap.page_allocator, args);
    // Check if there are any arguments
    if (args.len > 1) {
        m = args[1];
    }
    var key: [aead.chacha_poly.ChaCha12Poly1305.key_length]u8 = undefined;
    std.crypto.random.bytes(&key);

   var nonce: [aead.chacha_poly.ChaCha12Poly1305.nonce_length]u8 = undefined;
    std.crypto.random.bytes(&nonce);

   const ad = "Add";

   const ciphertext = try allocator.alloc(u8, m.len);
    defer allocator.free(ciphertext);

   var tag: [aead.chacha_poly.ChaCha12Poly1305.tag_length]u8 = undefined;
    aead.chacha_poly.ChaCha12Poly1305.encrypt(ciphertext, &tag, m, ad, nonce, key);
    const m2 = try allocator.alloc(u8, m.len);
    defer allocator.free(m2);
    const ct = ciphertext;

    try aead.chacha_poly.ChaCha12Poly1305.decrypt(m2, ct, tag, ad, nonce, key);

    try stdout.print("ChaCha12/Poly1305 (256-bit)\n", .{});
    try stdout.print("\nMessage: {s}\n", .{m});
    try stdout.print("\nKey:\t{x} \n", .{key});
    try stdout.print("Nonce:\t{x} Length: {d} bytes \n", .{ nonce, nonce.len });
    try stdout.print("AD:\t{s} \n", .{ad});
    try stdout.print("\nCiphertext: {x} \n", .{ciphertext});
    try stdout.print("  Tag:\t{x} \n", .{tag});
    try stdout.print("\nDecrypted: {s} \n", .{m2});
    try stdout.flush();
}

在 Microsoft Windows 上，我们使用以下命令编译为可执行文件 [ 这里]：

> zig build-exe zig_chacha.zig

然后我们可以运行文件 zig_chacha.exe。一个示例运行如下：

ChaCha12/Poly1305 (256-bit)

Message: Hello
Key:    cc04b1944b6713c91cd3a5b9c071b93bfb3faae911c8696a9b5e05cf0e809883
Nonce:  57e9f7227e19ee94f8a8da26 Length: 12 bytes
AD:     Add
Ciphertext: 9a2b50ed9a
  Tag:  ca460a48f55d81361db5f28d8f8b9fe4
Decrypted: Hello

我们可以看到密文长度与明文长度相同。我们正在使用 256 位的 ChaCha12/Poly1305 和 256 位（32 字节）的密钥。标签长度为 16 字节（128 位），nonce（盐/IV）值为 12 字节长（96 位）。

而且，如果我们愿意，我们可以将轮数减少到 8 轮，这更接近破解的边缘，但仍然为我们提供了出色的安全性。这为我们提供了 ChaCha8/Poly1305 [ 这里]：

const std = @import("std");
const aead = @import("std").crypto.aead;

pub fn main() !void {
    var gpa = std.heap.GeneralPurposeAllocator(.{}){};
    defer _ = gpa.deinit();
    const allocator = gpa.allocator();
    var stdout_buffer: [4096]u8 = undefined;
    var stdout_writer = std.fs.File.stdout().writer(&stdout_buffer);
    const stdout = &stdout_writer.interface;
    // Get the command-line arguments
    var m: []const u8 = undefined;
    const args = try std.process.argsAlloc(std.heap.page_allocator);
    defer std.process.argsFree(std.heap.page_allocator, args);
    // Check if there are any arguments
    if (args.len > 1) {
        m = args[1];
    }
    var key: [aead.chacha_poly.ChaCha8Poly1305.key_length]u8 = undefined;
    std.crypto.random.bytes(&key);
    var nonce: [aead.chacha_poly.ChaCha8Poly1305.nonce_length]u8 = undefined;
    std.crypto.random.bytes(&nonce);
    const ad = "Add";
    const ciphertext = try allocator.alloc(u8, m.len);
    defer allocator.free(ciphertext);
    var tag: [aead.chacha_poly.ChaCha8Poly1305.tag_length]u8 = undefined;
    aead.chacha_poly.ChaCha8Poly1305.encrypt(ciphertext, &tag, m, ad, nonce, key);
    const m2 = try allocator.alloc(u8, m.len);
    defer allocator.free(m2);
    const ct = ciphertext;
    try aead.chacha_poly.ChaCha8Poly1305.decrypt(m2, ct, tag, ad, nonce, key);
    try stdout.print("ChaCha8/Poly1305 (256-bit)\n", .{});
    try stdout.print("\nMessage: {s}\n", .{m});
    try stdout.print("\nKey:\t{x} \n", .{key});
    try stdout.print("Nonce:\t{x} Length: {d} bytes \n", .{ nonce, nonce.len });
    try stdout.print("AD:\t{s} \n", .{ad});
    try stdout.print("\nCiphertext: {x} \n", .{ciphertext});
    try stdout.print("  Tag:\t{x} \n", .{tag});
    try stdout.print("\nDecrypted: {s} \n", .{m2});
    try stdout.flush();
}

在 Microsoft Windows 上，我们使用以下命令编译为可执行文件：

> zig build-exe zig_chacha.zig

然后我们可以运行文件 zig_chacha.exe。一个示例运行如下 [ 这里]：

ChaCha8/Poly1305 (256-bit)

Message: Hello
Key:    b71ab16d10b3e199afbe6d90d601e3ada9838fe3388e591874dd847384b9b17c
Nonce:  96dfce06986c3793aaeaf1b8 Length: 12 bytes
AD:     Add
Ciphertext: 1ce4d023d5
  Tag:  dfdecdbbd78c27faf26e94511b762122
Decrypted: Hello

更大的 nonce — XChaCha20, XChaCha12 和 XChaCha8

在对称密钥方法中，我们需要确保对于同一个密钥，永远不要使用相同的 nonce。因此，我们使用 96 位的 nonce 大小，这样几乎不可能重用 nonce 值。对于某些应用，96 位的 nonce 值可能太小，因此 XChaCha20、XChaCha12 和 XChaCha8 为我们提供了 192 位的 nonce，在这种情况下，对于任何密钥来说，永远存在相同的 nonce 值几乎是不可能的：

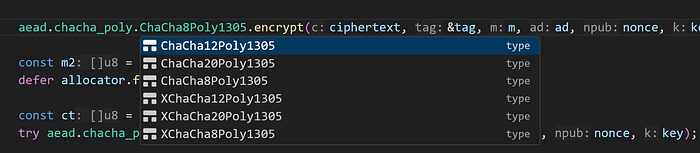
代码在这里：

Zig XChaCha20/Poly1305 AEAD

Daniel 呢？

Daniel J Bernstein（djb）出生于 1971 年。他是美国/德国公民，是埃因霍温理工大学的个人教授和伊利诺伊大学芝加哥分校的研究教授。

在 24 岁的妙龄 – 1995 年 – 他与电子前沿基金会（Electronic Frontier Foundation）一起对美国政府提起诉讼，涉及保护言论自由（Bernstein v. United States: 这里）。结果裁定软件应包含在第一修正案中。一个核心贡献是它减少了政府对加密的监管。这是即将来自 Daniel 惊人思想的伟大之处的征兆。他对当时降低密码学强度的观点是这样定义的：

“幸运的是，世界上没有很多恐怖分子。但是有很多罪犯利用互联网漏洞来获取经济利益。他们渗透计算机并窃取他们能找到的任何秘密，从个人信用卡号码到公司商业计划。也有相当多的破坏者只是为了好玩而制造麻烦。”

从那时起，很少有人为隐私事业做出如此多的贡献，包括在 2005 年创建 Sala20 [l ink] 流密码，然后在 2008 年创建 ChaCha20 [ link] 和 Poly1305。TLS 中的许多连接现在使用 ChaCha20 而不是 AES，因为它更快 – 比 AES 快三倍以上 – 并且计算要求更低。他对使用舞蹈名称的喜爱也体现在 Rumba [ 这里] 中。

他不仅在对称密钥加密方面做出了贡献，而且还在公钥加密方面做出了重大贡献。2005 年，他定义了 Curve 25519 椭圆曲线，它现在是定义椭圆曲线的一种相当标准的方式。对于签名，他随后定义了 Ed25519 以及新的 EdDSA 签名的结果版本（现在包含在 OpenSSH 中）。例如，Tor 协议对其安全路由中涉及的每个节点使用 Curve 25519 进行密钥交换。

他定义了用于 PQC 数字签名的 SPHINCS+ 方法。这是 NIST 批准的量子鲁棒签名方法之一。

2015 年，Daniel 定义了 NSA 可能用来破坏 NIST 定义的椭圆曲线的方法 [ 论文]。在 2005 年，Daniel 再次引入了一种新型的攻击 [ 这里]。

Daniel 从 https://cr.yp.to 运行他的网站

更多详情：https://medium.com/asecuritysite-when-bob-met-alice/a-lifetime-dedicated-to-citizens-rights-to-privacy-daniel-j-bernstein-ab5ab2bf0dc6

• 原文链接： medium.com/asecuritysite...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～