不管我们喜不喜欢，ECDSA都是比特币和以太坊的王者，是其信任基础设施的核心。虽然它的可扩展性不如EdDSA等方法，但在创建签名时稍加修改就可以实现一系列保护隐私的方法。在开始之前，让我们快速了解一下ECDSA是如何工作的。

ECDSA的基础知识

使用ECDSA签名，Alice 用她的私钥 (sk) 对消息的哈希 (h(M)) 进行签名，Bob用她的公钥(Pk)对其进行检查。使用ECDA， Alice生成一个私钥(sk)和一个公钥(Pk):

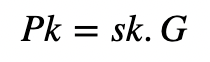
然后我们对消息进行哈希处理：

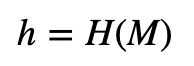
之后，Alice创建一个随机值k，并产生：

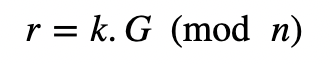
式中，r为k.G(对n取模)的x坐标值，则s值为：

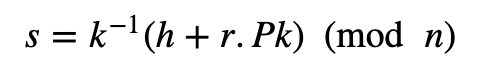
当Bob检查签名时，他计算：

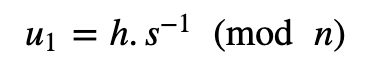
和：

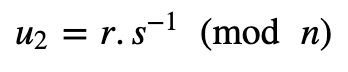
之后Bob计算一个点在：

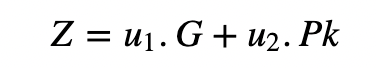
如果Z的x坐标的值等于r，则签名就被验证了。在这种情况下，n 是曲线的阶数。

盲化的ECDSA

使用盲签名，Bob可以在不知道消息是什么的情况下为消息签名。在这种情况下，Alice会创建一个“盲化”的ECDSA签名，Bob可以签名，然后Alice可以解除盲化。该方法是基于奥列格·安德烈夫(Oleg Andreev)的比特币盲签名方法。

首先，Alice生成a, b, c, d的四个随机值，Bob生成p, q的两个随机值，然后计算：

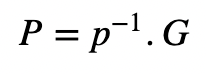
和：

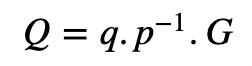
G是曲线的基点。Bob 将这些发送给 Alice。接下来，Alice 计算：

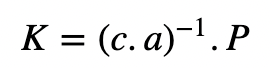
公钥：

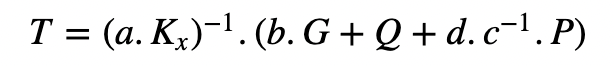
Alice计算消息(M)的哈希值：

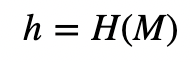
然后Alice进行盲化：

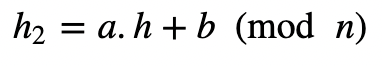
把这个发给Bob。Bob签署盲哈希并返回：

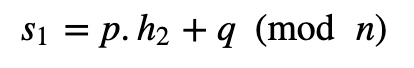
爱丽丝打开她的签名：

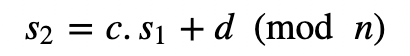
现在签名是r = K_x , s = s 2。

代码

下面是代码：

package main

import (
  "crypto/ecdsa"
  "crypto/elliptic"
  "crypto/rand"
  "crypto/sha256"
  "fmt"
  "math/big"
  "os"
  "strconv"
)

// Derived from Oleg Andreev
// Blind signatures for Bitcoin transactions

func main() {

  type Alice struct {
    m          *big.Int
    a, b, c, d *big.Int
  }

  type Bob struct {
    p, q *big.Int
  }
  bits := 16

  argCount := len(os.Args[1:])

  if argCount > 0 {
    bits, _ = strconv.Atoi(os.Args[1])
  }

  Curve := elliptic.P256()
  n := Curve.Params().N

  alice, bob := Alice{m: getRandom(n)}, Bob{}
  // Alice select random primes
  alice.a, alice.b, alice.c, alice.d = getRandomPrime(bits), getRandomPrime(bits), getRandomPrime(bits), getRandomPrime(bits)

  tmp, x, y := new(big.Int), new(big.Int), new(big.Int)

  // 2. Bob computes P = (p^-1 .G) and Q = (q.p^-1 .G)
  bob.p, bob.q = getRandomPrime(bits), getRandomPrime(bits)
  Px, Py := Curve.ScalarBaseMult(new(big.Int).ModInverse(bob.p, n).Bytes())
  Qx, Qy := Curve.ScalarBaseMult(new(big.Int).Mul(bob.q, new(big.Int).ModInverse(bob.p, n)).Bytes())

  // 3. Alice computes K = (c.a)^-1 .P and public key T = (a.Kx)^-1 .(b.G + Q + d.c^-1 .P).

  tmp = new(big.Int)
  Kx, _ := Curve.ScalarMult(Px, Py, tmp.Mul(alice.c, alice.a).ModInverse(tmp, n).Bytes())

  Tx, Ty := Curve.ScalarBaseMult(alice.b.Bytes())
  Tx, Ty = Curve.Add(Tx, Ty, Qx, Qy)
  x, y = Curve.ScalarMult(Px, Py, new(big.Int).Mul(alice.d, new(big.Int).ModInverse(alice.c, n)).Bytes())
  Tx, Ty = Curve.Add(Tx, Ty, x, y)
  tmp = new(big.Int)
  Tx, Ty = Curve.ScalarMult(Tx, Ty, tmp.Mul(alice.a, Kx).ModInverse(tmp, n).Bytes())

  // 4. Alice computes hash of message
  h := hashToInt(hash(alice.m.Bytes()), Curve)
  // 5. Alice blinds with h_2 = a.h + b (mod n) and sends to Bob
  tmp = new(big.Int)
  h2 := tmp.Mul(alice.a, h).Add(tmp, alice.b).Mod(tmp, n)

  // 6. Bob signs  blinded hash and returns s_1 = p.h_2 + q (mod n).

  tmp = new(big.Int)
  s1 := tmp.Mul(bob.p, h2).Add(tmp, bob.q).Mod(tmp, n)

  // 7. Alice unblinds signature: s_2 = c.s_1 + d (mod n)
  tmp = new(big.Int)
  s2 := tmp.Mul(alice.c, s1).Add(tmp, alice.d).Mod(tmp, n)

  // 8. The signature is now r=Kx, s=s_2
  fmt.Printf("m=%s\n\n", alice.m)
  fmt.Printf("a=%s\nb=%s\nc=%s\nd=%s\n", alice.a, alice.b, alice.c, alice.d)
  fmt.Printf("Public Key Tx=%s\nTy=%s\n", Tx, Ty)
  fmt.Printf("Hash h=%s\n\n", h)
  fmt.Printf("\nBlinded Signature r=%s, s=%s\n", Kx, s1)
  fmt.Printf("Signature r=%s, s=%s\n", Kx, s2)
  fmt.Println("Signature verified: ", ecdsa.Verify(&ecdsa.PublicKey{Curve: Curve, X: Tx, Y: Ty}, h.Bytes(), Kx, s2))

}
func getRandom(n *big.Int) *big.Int {
  m, _ := rand.Int(rand.Reader, n)
  return m
}
func getRandomPrime(bits int) *big.Int {
  m, _ := rand.Prime(rand.Reader, bits)
  return m
}

func hash(msg []byte) []byte {
  hasher := sha256.New()
  hasher.Write(msg)
  return hasher.Sum(nil)
}

func hashToInt(hash []byte, c elliptic.Curve) *big.Int {
  orderBits := c.Params().N.BitLen()
  orderBytes := (orderBits + 7) / 8
  if len(hash) > orderBytes {
    hash = hash[:orderBytes]
  }

  ret := new(big.Int).SetBytes(hash)
  excess := len(hash)*8 - orderBits
  if excess > 0 {
    ret.Rsh(ret, uint(excess))
  }
  return ret
}

下面是一个运行示例：

m=46398016479029616968153310998590589859317634753915956549813904092937392557159a=3303670661
b=3226384361
c=3530828149
d=3607703383
Public Key Tx=75232732142229191477159812086310547165062017290843364912683578530970424703230
Ty=73950523097040244239776555774732425845079447152113985190585097252768983601069
Hash h=53060989786633559228535141356889483919385714906876242047763586659314070909566Blinded Signature r=94046861866238546923597525972649788516701559058765278594626970725249113708126, s=103442503972324084972377390983720274585365710753545239530321864819095340728763
Signature r=94046861866238546923597525972649788516701559058765278594626970725249113708126, s=35825078730317479356116975137038450525621519055620748195720062041695485378112
Signature verified:  true

我们可以看到签名的真实性。运行代码如下:

https://asecuritysite.com/ecdsa/blinding_ecdsa

Source：https://medium.com/asecuritysite-when-bob-met-alice/blinding-ecdsa-8bc3493cac14

关于

ChinaDeFi - ChinaDeFi.com 是一个研究驱动的DeFi创新组织，同时我们也是区块链开发团队。每天从全球超过500个优质信息源的近900篇内容中，寻找思考更具深度、梳理更为系统的内容，以最快的速度同步到中国市场提供决策辅助材料。

本文首发于：https://mp.weixin.qq.com/s/npDpsnb7cY8ADXi9L_IZuA