什么是BLS签名以及它们如何工作？

Boneh-Lynn-Shacham (BLS) 多重签名是一种强大的密码学工具，它允许多个参与者共同生成一个单一、紧凑的签名。这些签名在共识机制中尤其有价值，例如以太坊，它们有助于减少签名大小并提高效率。

在这篇博文中，我们将深入研究 EigenLayer 的主动验证服务 (AVS) 合约中 BLS 多重签名的实现。EigenLayer 代表了区块链生态系统中的一个重要协议，它通过再质押扩展了以太坊的功能。通过使用 EigenLayer AVS 作为示例，我们超越了理论上的密码学构造，展示了 BLS 多重签名如何被用于解决现实世界的挑战。我们在本文中重点介绍了一些经常被忽视或没有记录的关键技术细节。我们还提出了一个在使用 BLS 多重签名时要避免的重要陷阱，EigenLayer 如何解决这个挑战，以及未来可能探索的替代方法。

理解 EigenLayer 的 AVS

EigenLayer 是一个建立在以太坊上的协议，它启用了再质押，以太坊质押者可以通过再质押来复用他们质押的 ETH，从而保护以太坊区块链之外的附加服务。这些附加服务在 EigenLayer 中被称为主动验证服务 (AVS)。以太坊质押者可以将他们质押的某些代币委托给负责验证 AVS 给出的一些任务的运营商。一些 AVS 已经在运行不同的服务，并且可以在这里↗找到已部署 AVS 的列表。

EigenLayer 创建了一个名为Incredible Squaring AVS↗的存储库，实现了一个 AVS 的玩具示例，以展示它在实践中是如何工作的。在这个简单的例子中，一个任务只是一个数字，并且该组运营商负责计算并签署该数字的平方。这是来自该存储库的图片，展示了它的工作原理：

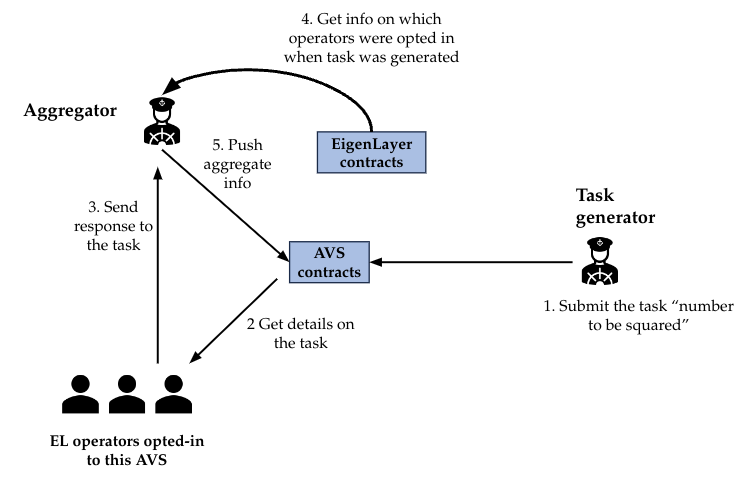
任务生成器负责将任务提交给 AVS 合约。在此示例中，任务由一个数字、任务创建时的区块号和一个阈值组成，该阈值指示运营商验证的百分比，这是验证任务所必需的。AVS 合约由 EigenLayer 开发，可在此处↗获得。但是，每个 AVS 可以根据自己的需要决定是否使用这些合约。

然后，选择加入 AVS 的运营商能够获得这些任务，计算任务答案（在前面的示例中，是数字的平方），并将答案及其任务的 BLS 签名发送给聚合器。

一旦达到相同答案的阈值，聚合器会将所有 BLS 签名合并为一个唯一的聚合签名，并将其发送回 AVS 合约。该合约验证签名是否正确，并开启一个挑战期，在此期间，挑战者可以提供验证不正确的证据，如果是这样，则行为不端的运营商将被罚没。

帖子的以下部分是关于 BLS 签名聚合的细节以及它在 AVS 合约中的实现方式。

定义 Boneh-Lynn-Shacham

我们简要回顾一下 Boneh-Lynn-Shacham (BLS) 签名是如何工作的。有关更详细的定义，请参阅参考论文↗。该签名使用两个不同的群 $\mathbb{G}_1, \mathbb{G}_2$，它们各自的生成器为 $G_1, G_2$。 然后密钥 sksksk 是一个 1 到 q 之间的随机数（$G_1$ 的阶）。相应的公钥为 $pk = sk \cdot G_2 \in \mathbb{G}_2$。要签署消息，我们需要一个哈希函数 $H: { 0,1 }^* \rightarrow \mathbb{G}_1$。此函数将任意消息映射到第一个群的元素。消息 $m$ 的签名由以下给出：

$$\sigma = sk \cdot H(m) \in \mathbb{G}_1$$

给定一个配对 $e$，为了验证签名 $\sigma$ 是否正确，验证者检查以下等式是否成立：

$e(H(m), pk) \stackrel{?}{=} e(\sigma, G_2)$

根据配对 $e$ 的双线性，如果签名正确，我们有

$$ \begin{split} e( H(m), pk) & = e(H(m), sk \cdot G_2) \ & = e(sk \cdot H(m), G_2) \ & = e(\sigma, G_2) \end{split} $$

要了解有关配对及其属性的更多信息，请参阅我们之前的博文↗。

关于前面的定义有一些说明。首先，由于配对验证是对称的，因此签名方案可以用另一种方式定义，即签名在 $\mathbb{G}_2$ 中，公钥在 $\mathbb{G}_1$ 中。大多数情况下，$\mathbb{G}_2$ 是在字段的二次扩展上定义的，并且 $\mathbb{G}_2$元素的存储更大。此外，$\mathbb{G}_2$中的算术比 $\mathbb{G}_1$中的算术更耗费资源。根据实现约束，切换公钥群可能是一个优势。如果实现需要存储所有签署消息的公钥，那么将它们放在 $\mathbb{G}_1$ 中以减少存储将更有趣。如果只能保留聚合公钥，但必须存储所有签名，则签名应在 $\mathbb{G}_1$ 中，公钥应在 $\mathbb{G}_2$中。

另一点是，由于验证涉及配对操作，这非常复杂，因此验证比其他椭圆曲线签名验证（如 Schnorr 或 EdDSA）更耗时。但是，BLS 签名允许直接签名聚合，这对于其他签名算法来说并不那么简单。

在 Solidity 合约中，大多数时候，使用的群是 BN254 曲线↗的子群。这允许使用 EIP-196↗ 和 EIP-197↗ 中定义的预编译合约，以节省大量 gas。然而，预编译合约施加了一些约束，因为它们只提供 $\mathbb{G}_1$ 中的操作，而不提供 $\mathbb{G}_2$ 中的操作。正如我们稍后将看到的，这迫使智能合约开发人员找到一些优化方法来避免在 $\mathbb{G}_2$ 中进行计算。

长期安全的另一个问题是，人们发现 BN254 曲线的安全级别约为 100 位↗，而不是之前认为的 128 位。为此，一些项目（如 Zcash↗）迁移到另一个名为 BLS12-381 的曲线，其安全级别更高。不要与名称“BLS”混淆；在这里，此曲线是 Barreto-Lynn-Scott 曲线↗的成员。以太坊 Pectra 升级↗ 现在还包括用于 BLS12-381 曲线的预编译合约，带有 EIP-2537↗。关于 BLS 签名的主要改进是包括了此曲线的 $\mathbb{G}_2$ 中的操作。

构建聚合签名和多重签名

签名聚合的概念是，当 $n$ 个参与者发布了 $n$ 个不同消息的 $n$ 个签名时，他们构建一个聚合签名 $\sigma_{\mathrm{agg}}$。当有效时，此聚合签名使验证者确信所有参与者都签署了它们的消息。

对于 BLS 签名，有一种自然的方法来构建聚合签名。假设我们有 $n$ 个消息的 $n$ 个签名 $\sigma0, \dots,\sigma{n-1}$。我们可以使用以下方法计算聚合签名，而不是独立验证它们：

$$\sigma{\mathrm{agg}} = \sum{i=0}^{n-1} \sigma_i$$

然后，验证算法变为

$$ e(\sigma_{\mathrm{agg}}, G_2) \stackrel{?}{=} e(H(m0), pk{0}) \cdot ... \cdot e(H(m{n-1}), pk{n-1})$$

聚合签名很小，是一个单一的群元素，并且它为验证节省了 $n-1$ 个配对评估。

多重签名的概念类似于聚合，但所有签名者都签署相同的消息 $m$。对于 BLS，它可以进一步优化验证。如果我们有相同消息 $m$ 的 $n$ 个签名，则验证变为

$e(\sigma_{\mathrm{agg}}, G2) \stackrel{?}{=} e\left(H(m), \sum{i=0}^{n-1} pk_{i}\right)$

无论签名数量如何，我们只需要两个配对评估。此外，我们可以定义一个聚合公钥

$apk = \sum_{i=0}^{n-1} pk_i$

以便为每个签名验证重用。

这种高效的方案在实践中被大量使用。例如，它在以太坊↗中用于将验证者投票聚合为单个签名。如前所述，它也是 AVS 的核心。这减少了验证时间和签名存储。有关实现 BLS 签名聚合或多重签名的良好信息来源是 IETF 草案↗，其中详细介绍了要使用的原语和要避免的一些陷阱。

此时可能会出现一个问题：是否可以使用 Schnorr 签名构建签名聚合？答案是肯定的。Schnorr 签名是线性的；因此，我们也可以聚合它们。然而，由于每个 Schnorr 签名都需要生成一个 nonce，因此与 BLS 的单轮通信相比，多重签名至少需要参与者之间的两轮通信。这使得 Schnorr 协议的实现更加复杂，并且更容易出错。MuSig2↗ 是实践中使用的一种 Schnorr 多重签名协议。在我们之前的关于比特币的博文↗中，我们更多地介绍了 Schnorr 多重签名和阈值签名的主题。

BLS 签名在 EigenLayer 中的样子

如前所述，EigenLayer 也在其 AVS 实现中使用 BLS 聚合。聚合器接收运营商当前任务的 BLS 签名；一旦收到足够的签名，它将它们聚合为单个签名，并将其与已签署消息的公钥一起发送到 BLSSignatureChecker 合约。为了验证签名，合约将所有公钥加在一起，并按照前面所述验证聚合签名。在合约中，验证发生在 trySignatureAndApkVerification 函数中：

function trySignatureAndApkVerification(
    bytes32 msgHash,
    BN254.G1Point memory apk,
    BN254.G2Point memory apkG2,
    BN254.G1Point memory sigma
) public view returns(bool pairingSuccessful, bool siganatureIsValid) {
    // gamma = keccak256(abi.encodePacked(msgHash, apk, apkG2, sigma))
    uint256 gamma = uint256(keccak256(abi.encodePacked(msgHash, apk.X, apk.Y, apkG2.X[0], apkG2.X[1], apkG2.Y[0], apkG2.Y[1], sigma.X, sigma.Y))) % BN254.FR_MODULUS;
    // verify the signature
    (pairingSuccessful, siganatureIsValid) = BN254.safePairing(
            sigma.plus(apk.scalar_mul(gamma)),
            BN254.negGeneratorG2(),
            BN254.hashToG1(msgHash).plus(BN254.generatorG1().scalar_mul(gamma)),
            apkG2,
            PAIRING_EQUALITY_CHECK_GAS
        );
}

值得注意的是，与我们之前介绍的相比，验证略有不同。首先，它采用两个公钥 apkapkapk 和 apk2apk_2apk2​，并且配对检查修改为以下内容：

$$ \begin{split} & e(\sigma + \gamma \cdot apk, G_2) \stackrel{?}{=} e(H(m) + \gamma \cdot G_1, apk_2)\ \Leftrightarrow \quad & e(\sigma, G_2) \cdot e(\gamma \cdot apk, G_2) \stackrel{?}{=} e(H(m), apk_2) \cdot e(\gamma \cdot G_1, apk_2) \ \end{split} $$

在重新排列这些项之后，我们可以将检查分为两部分：

$$ \begin{cases} \begin{equation}e(\sigma, G_2) \stackrel{?}{=} e(H(m), apk_2)\qquad\qquad\:\end{equation} \ \begin{equation}e(\gamma \cdot apk, G_2) \stackrel{?}{=} e(\gamma \cdot G_1, apk_2)\qquad\end{equation} \end{cases} $$

我们在第一个检查中发现了 BLS 验证。带有 γ\gammaγ 因子的第二个检查是先前 论文↗ 中描述的优化。正如我们所看到的，在 Solidity 中，EIP-196 预编译合约允许在 $\mathbb{G}_1$ 中执行操作，但是没有用于 $\mathbb{G}_2$ 操作的预编译合约。如果聚合器只发送了签名者的 $\mathbb{G}_2$ 中的公钥列表，那么聚合公钥必须在 $\mathbb{G}_2$ 中计算，这可能非常耗费 gas。相反，聚合器发送了签名者公钥的列表，但是是在 $\mathbb{G}_1$ 中，并且聚合密钥已经是 $apk_2 \in \mathbb{G}_2$。最后，(2) 中的检查只是为了确保 $apk_2$ 与从签名者的密钥 $apk$ 计算的值相匹配。正如我们之前看到的，如果操作在 BLS12-381 上完成，则不再需要 EIP-2537 的这个技巧。

$\gamma$ 是划分因子。它是在所有公共值上计算的，以防止恶意聚合器伪造签名。例如，如果 $\gamma$ 不包括签名和公钥，那么攻击者可以选择以下内容：

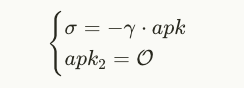
其中 $\mathcal{O}$ 是无穷远点。然后，该签名将验证任何消息 $m$。在前面的函数中，$\gamma$ 是在合约中使用以下方法计算的

$$ \gamma = \mathrm{keccak256}(m, apk, apk_2, \sigma) \mod q $$

防止签名伪造，因为 $\gamma$ 依赖于所有公共参数。与 Fiat–Shamir 启发式↗类似，$\gamma$ 必须依赖于所有验证参数，以防止恶意聚合器伪造签名。

正如 EigenLayer 文档中提到的，还有另一个威胁：

msgHash 是 apk 正在签名的哈希。请注意，调用者负责确保 msgHash 是哈希！如果有人可以提供任意输入，则可能会篡改签名验证。

实际上，如果哈希值 h=H(m)h = H(m)h=H(m) 可以由恶意运营商自由选择，通过设置以下内容：

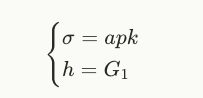
同样，对于任何消息 $m$，都将接受该签名。幸运的是，在前面的示例中，任务消息在传递给签名验证之前被哈希处理：

/* CHECKING SIGNATURES & WHETHER THRESHOLD IS MET OR NOT */
// calculate message which operators signed
bytes32 message = keccak256(abi.encode(taskResponse));

// check the BLS signature
(QuorumStakeTotals memory quorumStakeTotals, bytes32 hashOfNonSigners) =
    checkSignatures(message, quorumNumbers, taskCreatedBlock, nonSignerStakesAndSignature);

然而，AVS 合约有责任正确调用验证，因此检查这一点非常重要。

多重签名的陷阱

多重签名存在一个严重的潜在陷阱，称为 rogue-key 攻击。让我们举例说明这种攻击是如何工作的。

让我们假设一个诚实的用户有一个公钥 $pk_0$。然后，先前见过 $pk_0$ 的攻击者可以选择他们的公钥为 $pk_1 = sk_1 \cdot G_1 - pk_0$。攻击者不会知道与该公钥关联的私钥。然而，多重签名验证将给出以下内容：

$$ e(G1, \sigma) \stackrel{?}{=} e(pk_1 + pk_0, H(m)) = e( sk_1 \cdot G_1, H(m)) $$

只需要 $sk_1$ 来签署消息，从而产生有效的多重签名，即使第一个用户可能没有签署它。这很容易推广到任何数量 rrr 的诚实用户，通过选择 rogue key，即

$$ pk_r = sk_r \cdot G1 - \sum{i=0}^{r-1} pk_i$$

这是一个危险的威胁，因为在我们之前的 AVS 示例中，先前已注册 rogue key 的恶意聚合器可以发送未由验证者签名的聚合签名，但仍然会被合约接受。这将导致验证者即使没有不当行为也会受到惩罚。

防止陷阱

所有权证明

为了防止 rogue-key 攻击，一种常见的方法是要求用户证明他们知道与其公钥匹配的私钥。因此，在第一个注册步骤中，要求用户注册他们的公钥以及所有权证明 π\piπ，使得

$\pi = sk \cdot \tilde{H}(pk)$

基本上，要求用户签署他们的公钥或任何其他识别消息。然而，在证明中使用的哈希函数 $\tilde{H}$ 必须与聚合签名验证使用的哈希函数不同。实际上，$\tilde{H}$ 的构建是通过使用域分离来实现的，如 IETF 草案↗ 中解释的那样。

然后，聚合器通过使用另一个哈希函数 $\tilde{H}$ 使用 BLS 验证算法来验证所有权证明 $\pi$ 来注册公钥。

在 EigenLayer 合约中，所有权证明由 registerBLSPublicKey 函数验证：

function registerBLSPublicKey(
    address operator,
    PubkeyRegistrationParams calldata params,
    BN254.G1Point calldata pubkeyRegistrationMessageHash
) external onlyRegistryCoordinator returns (bytes32 operatorId) {
    // [...]

    // gamma = h(sigma, P, P', H(m))
    uint256 gamma = uint256(keccak256(abi.encodePacked(
        params.pubkeyRegistrationSignature.X,
        params.pubkeyRegistrationSignature.Y,
        params.pubkeyG1.X,
        params.pubkeyG1.Y,
        params.pubkeyG2.X,
        params.pubkeyG2.Y,
        pubkeyRegistrationMessageHash.X,
        pubkeyRegistrationMessageHash.Y
    ))) % BN254.FR_MODULUS;

    // e(sigma + P * gamma, [-1]_2) = e(H(m) + [1]_1 * gamma, P')
    require(BN254.pairing(
        params.pubkeyRegistrationSignature.plus(params.pubkeyG1.scalar_mul(gamma)),
        BN254.negGeneratorG2(),
        pubkeyRegistrationMessageHash.plus(BN254.generatorG1().scalar_mul(gamma)),
        params.pubkeyG2
    ), "BLSApkRegistry.registerBLSPublicKey: either the G1 signature is wrong, or G1 and G2 private key do not match");

    operatorToPubkey[operator] = params.pubkeyG1;
    operatorToPubkeyHash[operator] = pubkeyHash;
    pubkeyHashToOperator[pubkeyHash] = operator;

    emit NewPubkeyRegistration(operator, params.pubkeyG1, params.pubkeyG2);
    return pubkeyHash;
}

与之前的公钥和签名验证一样，这里也应用了相同的技巧。但是，正如之前解释的，哈希的计算方式不同。使用 pubkeyRegistrationMessageHash 函数：

function pubkeyRegistrationMessageHash(address operator) public view returns (BN254.G1Point memory) {
    return BN254.hashToG1(
        _hashTypedDataV4(
            keccak256(abi.encode(PUBKEY_REGISTRATION_TYPEHASH, operator))
        )
    );
}

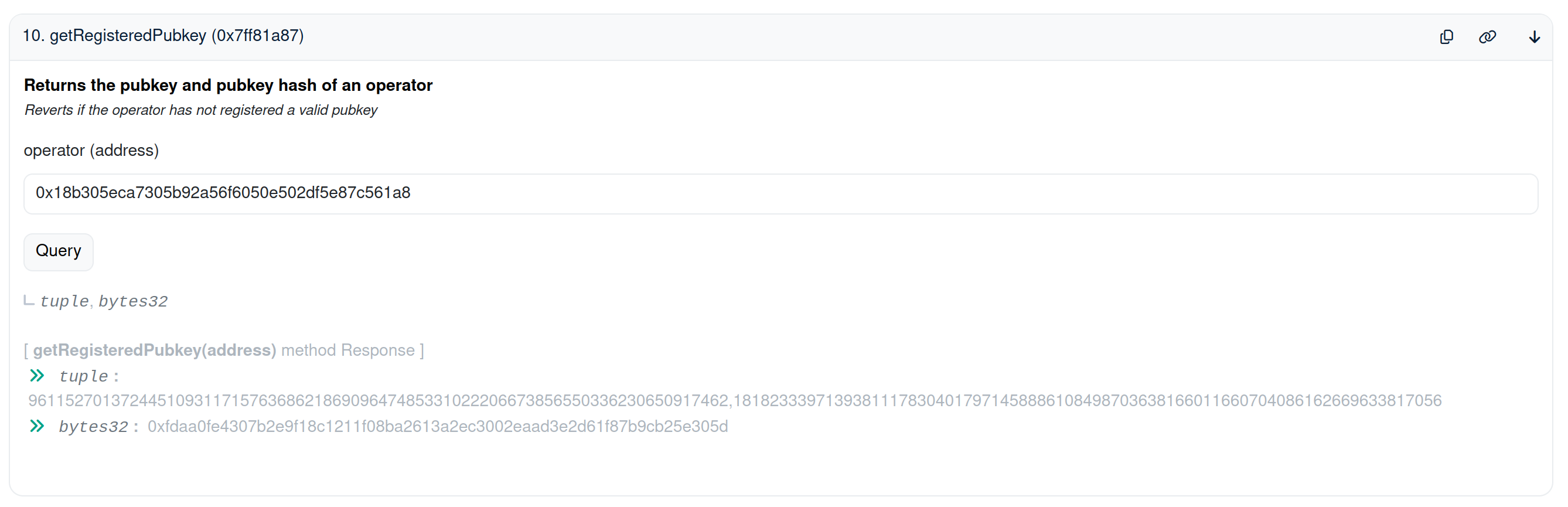
哈希函数使用自定义域分隔符 PUBKEY_REGISTRATION_TYPEHASH 来构建不同的哈希函数，并且消息只是运营商地址。注册后，公钥将添加到合约中。我们可以通过调用 getRegisteredPubkey 函数来验证其值。这是一个为 EigenDA AVS 注册的 BLS 公钥的示例：

对于这部分，使用不同的哈希函数非常重要。让我们看看如果我们使用与 BLS 签名中使用的哈希函数 HHH 相同会发生什么。这是所有权证明：

$\pi = sk \cdot H(pk)$

如果攻击者能够请求 $pk{\mathrm{agg}}$ 的聚合签名 $\sigma{\mathrm{agg}}$，那么他们可以通过发送以下证明来注册 rogue key

$pk = sk \cdot G1 - pk{\mathrm{agg}}$

$\pi = sk \cdot H(pk) - \sigma_{\mathrm{agg}}$

然后，这将允许攻击者执行 rogue-key 攻击，如前所述。因此，使用域分离至关重要。

所有权证明基本上是 BLS 签名。然而，也不建议在所有权证明步骤中使用多重签名，例如，为单个参与者注册多个公钥。如果是这样，参与者将实现 分裂零攻击↗。在这种情况下，参与者可以注册在加在一起时会抵消的密钥，并且可以绕过所有权证明。

修改后的聚合公钥

需要注意的一件事是，可以避免为 BLS 聚合多重签名实现所有权证明的负担。2018 年，Boneh et al. 提出了一个修改后的方案↗，其中可以聚合 BLS 签名，而没有 rogue-key 攻击的威胁，也没有所有权证明。到目前为止，我们还没有看到此解决方案在 EigenLayer AVS 或其他解决方案中实现，但将来可能是一个可能性。

为了聚合 $n$ 个签名，他们使用了一个哈希函数 $H_n: {0,1}^* \rightarrow Z_q^n$。然后，他们生成一个向量 $(t0,\dots, t{n-1}) = H_n (pk0, \dots, pk{n-1})$。修改后的聚合公钥为

$apk = \sum_i t_i \cdot pk_i$

聚合签名通过以下方式计算：

$\sigma = \sum_i t_i \cdot \sigma_i$

验证的工作方式与先前的聚合签名相同，只是使用了修改后的聚合公钥。由于此方案是 BLS 的修改版本，因此它可能与现有实现不兼容。但是，将其用于新实现可能会很有趣。这将消除密钥注册和工作量证明的需要，并简化现有方案。

结论

我们已经看到，BLS 多重签名提供了一个重要的优化机会。EigenLayer 的实现展示了 BLS 签名的强大功能，并且还强调了其实际部署中涉及的复杂性。然而，正如所讨论的，多重签名会带来安全风险，例如 rogue-key 攻击，这需要所有权证明之类的防护措施。我们还注意到，对于 Solidity 合约，许多优化是可能的。

随着 Pectra 升级支持 BLS12-381，我们可能会在 Solidity 中看到更多的实现和改进，因此我们希望这篇文章有助于避免已知的实现错误和漏洞。此外，替代的聚合方案（例如，抗 rogue-key 攻击的方法）为未来的发展提供了有希望的方向。

• 原文链接： zellic.io/blog/bls-signa...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～