零知识证明 - FPGA vs. GPU
- Star Li
- 发布于 2022-09-19 15:05
- 阅读 11440
本文从MSM的计算入手,分析FPGA和GPU加速零知识证明计算的优缺点。
零知识证明技术应用越来越广,隐私证明,计算证明,共识证明等等。在寻找更多更好的应用场景的同时,很多人逐步发现零知识证明证明性能是个瓶颈。Trapdoor Tech团队从2019年开始深入研究零知识证明技术,并一直探索高效的零知识证明加速方案。GPU或者FPGA是目前市面上比较常见的加速平台。本文从MSM的计算入手,分析FPGA和GPU加速零知识证明计算的优缺点。
TL;DR
ZKP是拥有未来广泛前景的技术。越来越多的应用开始采用零知识证明技术。但ZKP算法比较多,各种项目使用不同的ZKP算法。同时,ZKP证明的计算性能比较差。本文详细分析了MSM算法,椭圆曲线点加算法,蒙哥马利乘法算法等等,并对比了GPU和FPGA在BLS12_381曲线点加的性能差别。总的来说,在ZKP证明计算方面,短期GPU优势比较明显,Throughput高,性价比高,具有可编程性等等。FPGA相对来说,功耗有一定的优势。长期看,有可能出现适合ZKP计算的FPGA芯片,也可能为ZKP定制的ASIC芯片。
ZKP算法复杂
ZKP是个零知识证明技术的统称(Zero Knowledge Proof)。主要由两种分类:zk-SNARK以及zk-STARK。zk-SNARK目前常见的算法是Groth16,PLONK,PLOOKUP,Marlin和Halo/Halo2。zk-SNARK算法的迭代主要是沿着两条方向:1/是否需要trusted setup 2/电路结构的性能。zk-STARK算法的优势是毋需trusted setup,但是验证计算量是对数线性的。
就zk-SNARK/zk-STARK算法的应用来看,不同项目使用的零知识证明算法相对分散。zk-SNARK算法应用中,因为PLONK/Halo2算法是universal(无需trusted setup),应用可能越来越多。
PLONK证明计算量
以PLONK算法为例,剖析一下PLONK证明的计算量。
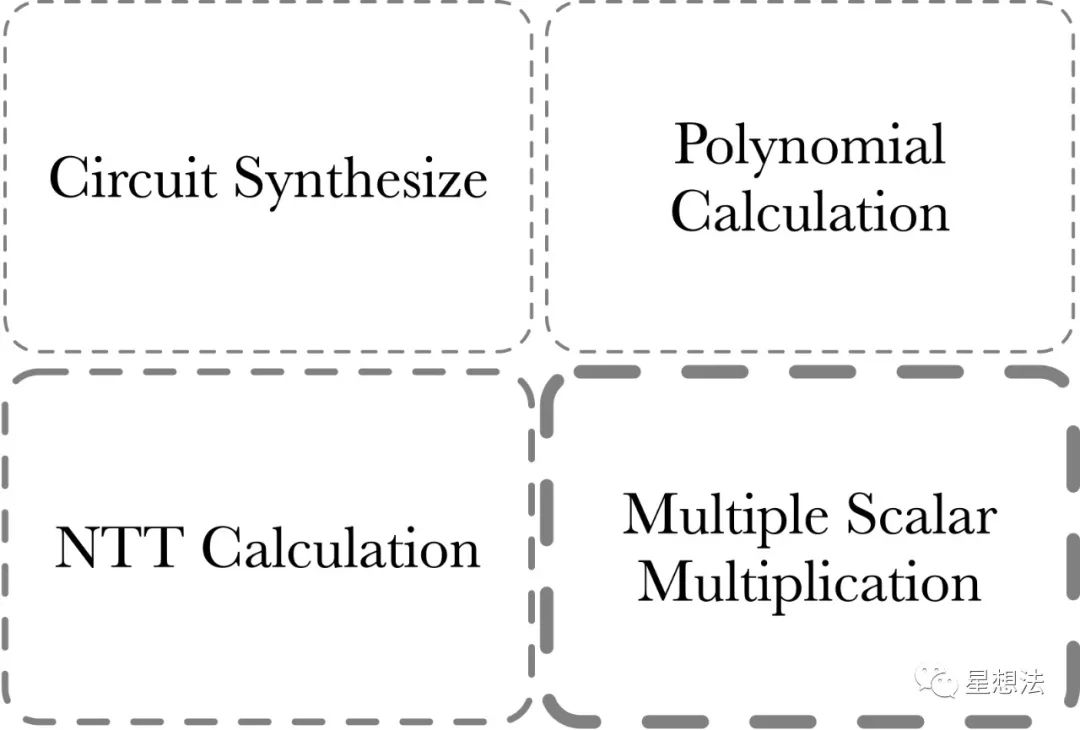
PLONK证明部分的计算量由四部分组成:
1/ MSM - Multiple Scalar Multiplication。MSM经常用来计算多项式承诺。
2/ NTT计算 - 多项式在点值和系数表示之间变换。
3/ Polynomial计算 - 多项式加减乘除。多项式求值(Evaluation)等等。
4/ Circuit Synthesize - 电路综合。这部分的计算和电路的规模/复杂度有关。
Circuit Synthesize部分的计算量一般来说判断和循环逻辑比较多,并行度比较低,更适合CPU计算。通常来讲,零知识证明加速一般指的是前三部分的计算加速。其中,MSM的计算量相对来说最大,NTT次之。
What's MSM?
MSM(Multiple Scalar Multiplication)指的是给定一系列的椭圆曲线上的点和标量,计算出这些点加的结果对应的点。
比如说,给定一个椭圆曲线上的一系列的点:
Given a fixed set of Elliptic curve points from one specified curve:
[G_1, G_2, G_3, ..., G_n] 以及随机的系数:
and a randomly sampled finite field elements from specified scalar field:
[s_1, s_2, s_3, ..., s_n] MSM is the calculation to get the Elliptic curve point Q:
Q = \sum_{i=1}^{n}s_i*G_i 行业普遍采用Pippenger算法对MSM计算进行优化。深入看看Pippenger算法的过程的示意图:
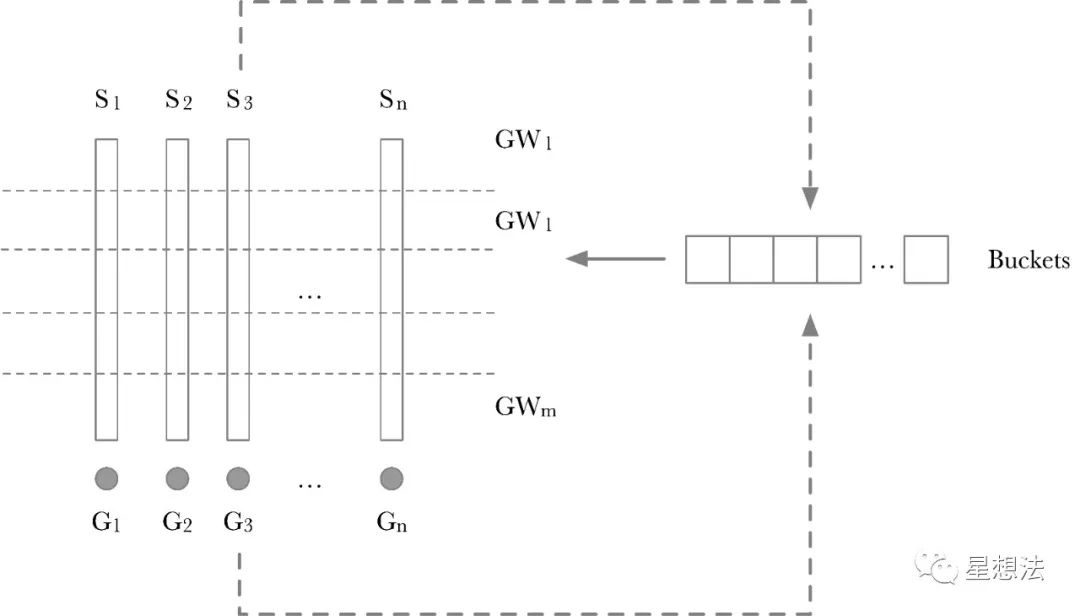
Pippenger算法的计算过程分成两步:
1/ Scalar切分为Windows。如果Scalar是256bits,并且一个Window是8bits,则所有的Scalar切分为256/8=32个Window。每一层的Window,采用一个“Buckets”临时存放中间结果。GW_x就是一层上的累加结果的点。计算GW_x也比较简单,依次遍历一层中的每个Scalar,根据Scalar这层的值作为Index,将对应的 G_x加到相应的Buckets的位上。其实原理也比较简单,如果两个点加的系数相同,则先将两个点相加后再做一次Scalar加,而不需要两个点做两次Scalar加后再累加。
2/ 每个Window计算出来的点,再通过double-add的方式进行累加,从而得到最后的结果。
Pippenger算法也有很多变形优化算法。不管怎么说,MSM算法的底层计算就是椭圆曲线上的点加。不同的优化算法,对应不同的点加个数。
椭圆曲线点加(Point Add)
你可以从这个网站看看具有“short Weierstrass”形式的椭圆曲线上点加的各种算法。
http://www.hyperelliptic.org/EFD/g1p/auto-shortw-jacobian-0.html#addition-madd-2007-bl
假设两个点的Projective坐标分别为(x1, y1, z1) 和 (x2, y2, z2) ,则通过如下的计算公式可以计算出点加的结果(x3, y3, z3)。
Z1Z1 = Z12
U2 = X2*Z1Z1
S2 = Y2*Z1*Z1Z1
H = U2-X1
HH = H2
I = 4*HH
J = H*I
r = 2*(S2-Y1)
V = X1*I
X3 = r2-J-2*V
Y3 = r*(V-X3)-2*Y1*J
Z3 = (Z1+H)2-Z1Z1-HH详细给出计算过程的原因是想表明整个计算过程绝大部分是整数运算。整数的位宽取决于椭圆曲线的参数。给出一些常见的椭圆曲线的位宽:
-
BN256 - 256bits
-
BLS12_381 - 381bits
-
BLS12_377 - 377bits
特别注意的是,这些整数运算是在模域上的运算。模加/模减相对来说简单,重点看看模乘的原理和实现。
模乘 (Modular Muliplication)
给定模域上的两个值:x和y。模乘计算指的是 x*y mod p。注意这些整数的位宽是椭圆曲线的位宽。模乘的经典算法是蒙哥马利乘法(Montgomery Muliplication)。在进行蒙哥马利乘法之前,被乘数需要转化为蒙哥马利表示:
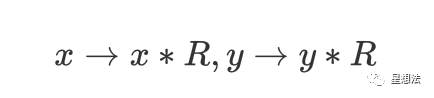
蒙哥马利乘法计算公式如下:
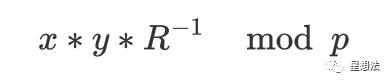
蒙哥马利乘法实现算法又有很多:CIOS (Coarsely Integrated Operand Scanning),FIOS(Finely Integrated Operand Scanning),以及 FIPS(Finely Integrated Product Scanning)等等。本文不深入介绍各种算法实现的细节,感兴趣的读者可以自行研究。
为了对比FPGA以及GPU的本身的性能差别,选择最基本的算法实现方法:
1. t = a * b
2. m = (t * n') mod r
3. tmp = t + m * n
4. u= tmp / r
5. if (u > n) result = u - n else result = u简单的说,模乘算法可以进一步分成两种计算:大数乘法和大数加法。理解了MSM的计算逻辑的基础上,可以选择模乘的性能(Throughput)来对比FPGA和GPU的性能。
DSP in Xilinx FPGA
Xilinx FPGA的UltraScale+系列是最新的产品线。VU9P是中端产品。AWS FPGA云平台也是采用VU9P芯片。
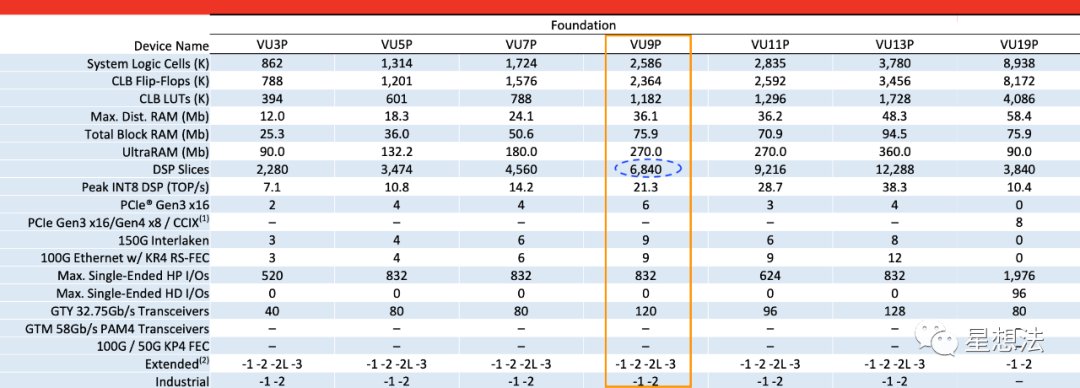 FPGA自带的DSP是宝贵的资源。为了保证系统clock,采用DSP设计大数模乘(包括大数乘法和大数加法)。VU9P内部的DSP信号是DSP48E2,其逻辑功能图如下:
FPGA自带的DSP是宝贵的资源。为了保证系统clock,采用DSP设计大数模乘(包括大数乘法和大数加法)。VU9P内部的DSP信号是DSP48E2,其逻辑功能图如下:
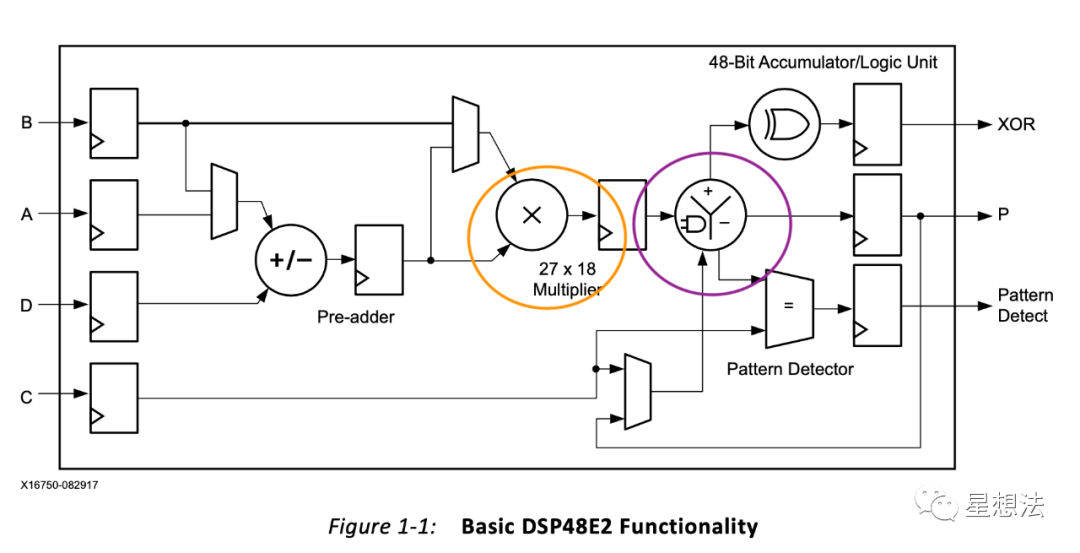
DSP48E2核心逻辑由一个27 18的乘法器以及一个算术计算器(加减/逻辑操作)。为了防止乘法溢出,在进行大数乘法计算时,可以把DSP48E2当作17 17的模块。
Pipelined Modular Multiplication in FPGA
为了对比FPGA和GPU的Modular Multiplication的性能,选定BLS12_381曲线。也就是说,模乘的位宽是381bit。利用FPGA的DSP的缘故,为了17bits对齐,位宽扩展为391bits(23*17bits)。
整个Pipelined Modular Multiplication的设计逻辑如下:
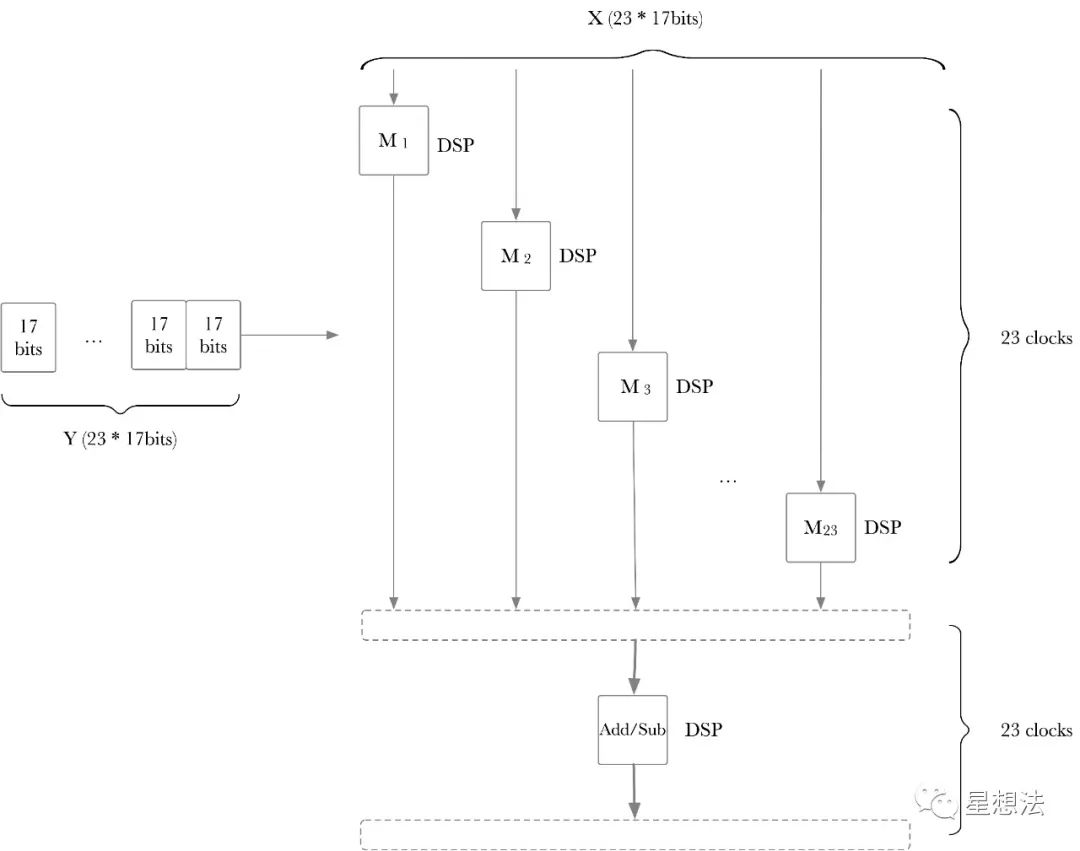
模乘的电路模块总共采用25个DSP,并分为两部分,一部分由23个DSP组成,实现大数乘法,另外一部分由2个DSP组成分别实现大数加/减。显然可以发现,大数乘法需要23 clocks完成,每个clock完成X*17bits。大数加和大数减的计算因为采用一个DSP,也需要23 clocks完成。这样的设计下,大数乘法的内部计算是pipeline的,大数乘法和大数加/减之间也是pipeline的。
因为模乘需要3个大数乘法和若干个大数加/减,*381bits的模乘计算需要323=69个clocks**。
观察和思考
在这样的FPGA设计下,可以估算出整个VU9P能提供的在BLS12_381椭圆曲线点加Throughput。一个点加(add_mix方式)大约需要12个模乘。FPGA的系统时钟为450M。
(6840/25)*(450/69)/12 = 104.3M/s在同样的模乘/模加算法下,采用同样的点加算法,Nvidia 3090的点加Troughput(考虑到数据传输因素)超过500M/s。当然,整个计算涉及到多种算法,可能存在某些算法适合FPGA,有些算法适合GPU。采用一样的算法对比的原因,想对比FPGA和GPU的核心计算能力。
在这样的计算能力差异下,再分析一下性价比的差异:
- Xilinx VU9P board - $8394
https://www.xilinx.com/products/boards-and-kits/vcu118.html
- Nvidia 3090 - $1499
在这样的情况下,我们来看看产品的性价比:
8394*500/1499/104.3 = 26.8也就是说,从性价比的角度看,Nvidia 3090是Xilinx VU9P的26倍。
Note:有关Xilinx VU9P的开发板,本身量比较少。能查到的公开价格也比较少,可能价格有偏差。其他FPGA芯片的性价比可以按照类似的逻辑进行计算。
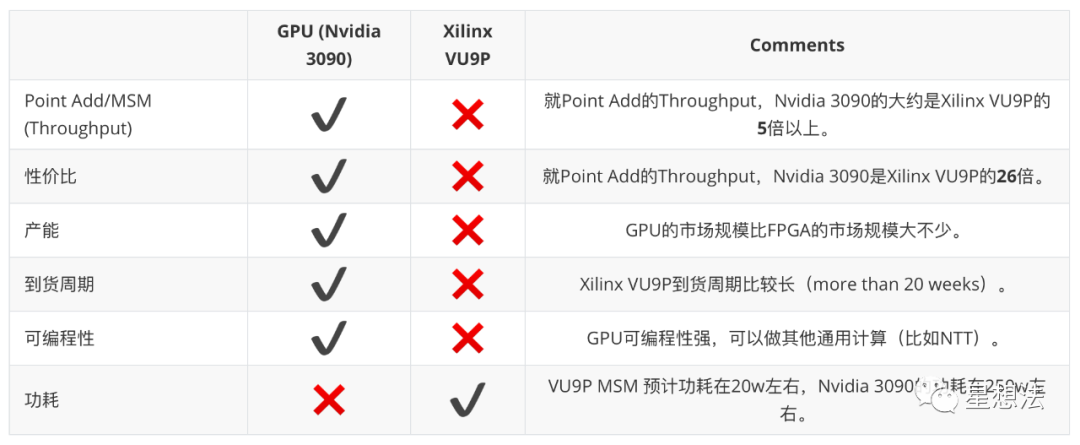
基于上述的结果,总结一下GPU和FPGA在ZKP证明性能方面的比较:
More powerful FPGA AI Engine
Xilinx的VCK5000平台,采用VC1902芯片(7nm工艺),实现AI加速引擎。价格相对便宜:$2,745.00。
https://www.xilinx.com/products/boards-and-kits/vck5000.html
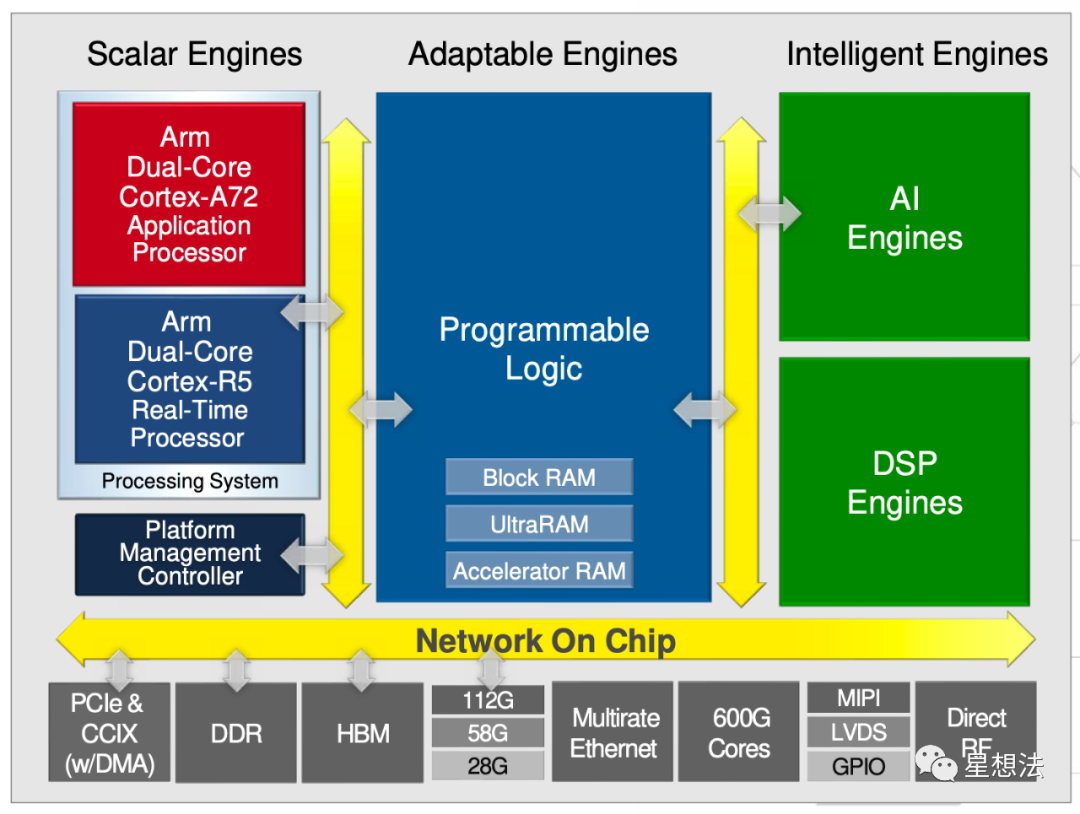
这款芯片除了可编程逻辑外(Programmable Logic),还配备了AI和DSP引擎。DSP引擎由1968个DSP58组成。AI引擎由400个AI Core组成。目前还不确定在这种芯片上的MSM/FFT的性能,不过值得期待。
总结:
越来越多的应用开始采用零知识证明技术。但ZKP算法比较多,各种项目使用不同的ZKP算法。从我们的实践工程经验来看,FPGA是个选项,但是目前GPU是个性价比高选项。FPGA偏好确定性计算,有latency以及功耗的优势。GPU可编程性高,有相对成熟的高性能计算的框架,开发迭代周期短,偏好需要throughput场景。

- ZK编年史:哈希登场 84 浏览
- Layer Zero 发布 Zero 链:去中心化的多核世界计算机 313 浏览
- “Jolt Inside” - 构建者需要了解的全新武器 265 浏览
- 以太坊的下一个重大转变:从重新执行每笔交易到验证 ZK 证明 337 浏览
- Zcash:比特币遗忘的隐私 413 浏览
- ZK编年史:计算模型 285 浏览
- lambdaworks 2026 年更新路线图和优先级 340 浏览
- 2026年构建机构级DeFi平台真正需要什么 850 浏览
- zkMesh:2026年1月回顾 437 浏览
- 如果它能编译,那它就是正确的(几乎):Lean 4 在 ZK 系统和工程中的介绍 615 浏览
- Zcash 的时代到来了 734 浏览
- ZK 编年史:电路(第二部分) 412 浏览

