默克尔树(Merkle Patricia Tree)详解
- Ellen
- 发布于 2023-01-20 16:59
- 阅读 9594
默克尔树(MerklePatriciaTree)在以太坊中是一种通用的,用来存储键值对的数据结构,可以简称为“MPT”,是字典树Redixtree的变种,也是以太坊的核心算法
一、概念
本文是阅读《深入以太坊智能合约开发》的附录A Merkle Patricia Tree后的知识归纳以及扩展。
默克尔树(Merkle Patricia Tree)在以太坊中是一种通用的,用来存储键值对的数据结构,可以简称为“MPT”,是字典树Redix tree的变种,也是以太坊的核心算法之一。
MPT对于树中节点的插入、查找、删除操作,这种结构可以提供对数级别的复杂度O(log(N)),所以它是一种相对高效的存储结构。
二、如何根据键值对构造默克尔树
2.1 节点类型
树类型的数据结构,都会有节点的概念,MPT也不例外。
MPT中有三种节点类型:branch、leaf、extension:
-
branch(分支)
- 由17个元素组成的元组,格式为:(v0,……,v15,vt)。
- 其中,v0~v15的元素是以其索引值(0x0~0xf)为路径的子节点数据的keccak256哈希值,如果没有子节点数据则元素为空。
- vt为根节点到当前节点的父节点所经过的路径对应的value值,也就是根节点到父节点所经过的路径组成了一个键key,这个key对应的value存在vt里面,如果这个key没有对应的value,那么vt为空。
-
leaf(叶)
- 两个元素组成的元组,格式为:(encodePath,value)
- encodedPath为当前节点路径的十六进制前缀编码
- value是从根节点到当前节点路径组成的键对应的值
-
extension(扩展)
- 两个元素组成的元组,格式为:(encodePath,key)
- encodedPath为当前节点路径的十六进制前缀编码
- key为当前节点子节点数据的keccak256哈希值
总结一下上述的那一堆概念:
-
键值对
-
extension节点记录着:路径、子节点的哈希值。
-
leaf节点记录着:路径、vlaue。
-
branch记录着:以索引值为路径的子节点的哈希值、从根节点到branch的父节点路径组成的键对应的value。
-
value值在leaf和branch节点中存放,key被拆解开,最终由extension、leaf的encodePath以及branch的索引值组成。
2.2 十六进制前缀编码
branch和extension元组的第一个元素encodePath就是当前节点路径的十六进制前缀编码(Hex-Pretix Encoding,HP编码)。使用HP编码能够区分节点是扩展结点还是叶子节点。 而HP编码,和当前节点类型还有当前路径半字节长度的奇偶有关。
半字节是4位二进制,即1位16进制。
0xf是半字节,0xff是1字节。
1111是半字节,11111111是1字节。
共有四种前缀:
| 路径所对应的节点类型 | 路径长度 | 二进制数值 | 十六进制数值 | 最终前缀(HP前缀) |
|---|---|---|---|---|
| Extension | 偶数个半字节 | 0000 | 0x0 | 0x00 |
| Extension | 奇数个半字节 | 0001 | 0x1 | 0x1 |
| Leaf | 偶数个半字节 | 0010 | 0x2 | 0x20 |
| Leaf | 奇数个半字节 | 0011 | 0x3 | 0x2 |
所以extension节点有两种前缀:0x00、0x1;leaf有两种前缀:0x20、0x3。
可以看到最终前缀在偶数个半字节0x0、0x2后补了一个0,变成了0x00,0x20,目的是为了凑成整字节,避免出现半字节导致长度不便于合并。
HP前缀需要放在原始路径前面去组成HP编码,实例:
| 原始数据 | 节点类型 | HP前缀 | HP编码 |
|---|---|---|---|
| (0x012345,key)(注:012345长度为偶数) | Extension | 0x00 (0000 0000) | (0x00012345,key) |
| (0x12345,key)(注:12345长度为奇数) | Extension | 0x1 (0001) | (0x12345,key) |
| (0x0f1cb8,value)(注:0f1cb8长度为偶数) | Leaf | 0x20 (0010 0000) | (0x200f1cb8,value) |
| (0xf1cb8,value)(注:f1cb8长度为奇数) | Leaf | 0x3 (0011) | (0x3f1cb8,value) |
2.3 构造一颗默克尔树
上面的概念不容易理解,现在我们以下面的例子,一步步来进行树的构造,帮助我们更好的理解:
我们假设有一组(4个)键值对数据需要用树来存储:
<64 6f> : 'verb'
<64 6f 67> : 'puppy'
<64 6f 67 65> : 'coin'
<68 6f 72 73 65> : 'stallion'
为方便解释说明以及阅读,我们把键值对数据的“键”表示为十六进制字符串,“值”则保留为原始字符串。在实际使用时,它们都需要经过特定的编码变换。
1.
<64 6f> : 'verb'
<64 6f 67> : 'puppy'
<64 6f 67 65> : 'coin'
<68 6f 72 73 65> : 'stallion'
每棵树都有根节点,默克尔树的根节点会保存当前路径和子节点哈希,所以很明显,根节点会是一个extension节点。
上面节点类型介绍了extension格式为:(encodePath,key),encodePath是十六进制的HP编码。分析给出的4个键我们可以得出都是以6开头,后面分为4、8两条路。所以根节点存储的共同路径值为0x6。
由于0x6只有一位,所以路径长度是奇数,节点又是extension类型,所以HP前缀是0x1,组合出来的HP编码:0x16。
所以当前默克尔树如下图:
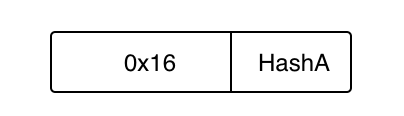
HashA代表着子节点的哈希值。
2.
<64 6f> : 'verb'
<64 6f 67> : 'puppy'
<64 6f 67 65> : 'coin'
<68 6f 72 73 65> : 'stallion'
根节点已经找到,但在根节点后出现了两条路,这个时候需要使用branch来处理这种多条路径的情况。
上文说到,branch由17个元素组成的元组,格式为:(v0,……,v15,vt)。其中,v0~v15是以其索引值(0x0~0xf)为路径的子节点数据的keccak256哈希值,如果没有子节点数据则为空。
这里4和8就是索引值,4、8对应元素是其字节点的哈希值。
所以当前默克尔树如下图:

3.
<64 6f> : 'verb'
<64 6f 67> : 'puppy'
<64 6f 67 65> : 'coin'
<68 6f 72 73 65> : 'stallion'
我们可以观察到,在0x68后只有唯一路径了,即0x6f727356,而value为“stallion”,所以不再分叉的情况下,就不是branch或者extension了,而应该是一个叶节点。
上文提到,leaf节点是两个元素组成的元组,格式为:(encodePath,value),encodedPath为当前节点路径的十六进制前缀编码,value是从根节点到当前节点路径组成的键,所对应的值。
当前节点的路径是0x6f727356,长度是偶数,节点类型是leaf,所以可以得出HP前缀是0x20,HP编码是0x206f727356。所以可得该leaf节点:(0x206f727356,"stallion")。
所以当前默克尔树如下图:
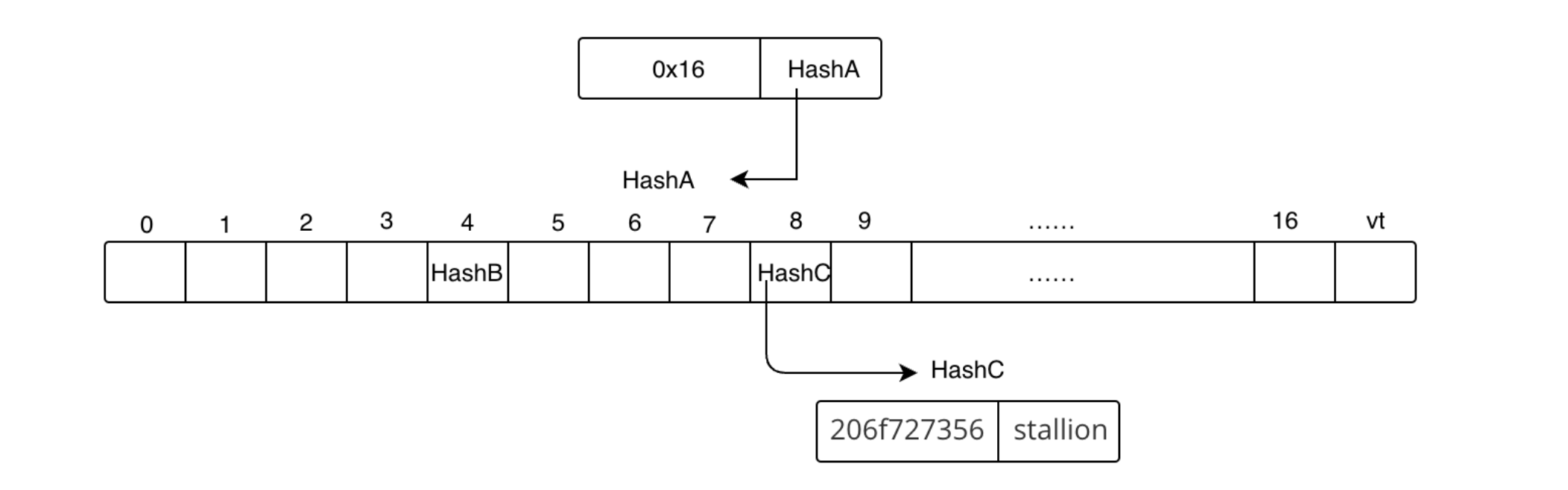
4.
<64 6f> : 'verb'
<64 6f 67> : 'puppy'
<64 6f 67 65> : 'coin'
<68 6f 72 73 65> : 'stallion'
说完了8,我们再说说4这部分,路径4后面有共同路径6f,6f后才产生null和6两条分叉。
共同路径6f是一个extension节点,extension节点格式不再介绍,开始计算HP编码,6f长度是偶数,又是extension类型,所以HP前缀为0x00,HP编码为0x006f。
所以当前默克尔树如下图:
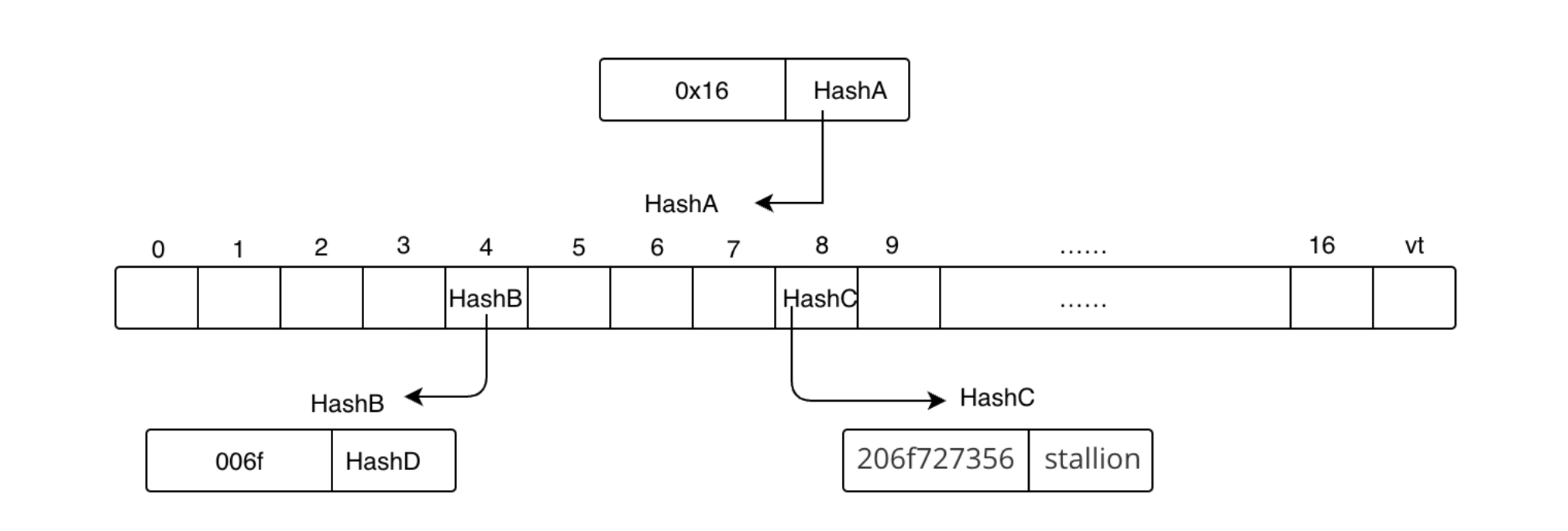
5.
<64 6f> : 'verb'
<64 6f 67> : 'puppy'
<64 6f 67 65> : 'coin'
<68 6f 72 73 65> : 'stallion'
6f后分出了null和6,是多条路径,所以HashD的节点是一个branch节点,6是索引值,索引为6的元素存储着子节点hash;而null是没有的,上文提到:vt为根节点到当前节点的父节点所经过的路径组成的键对应的value。
则代表当前HashD节点该存储从根节点到父节点0x646f组成的键对应的值:'verb'。那么该由HashD的vt保存'verb'。
所以当前默克尔树如下图:
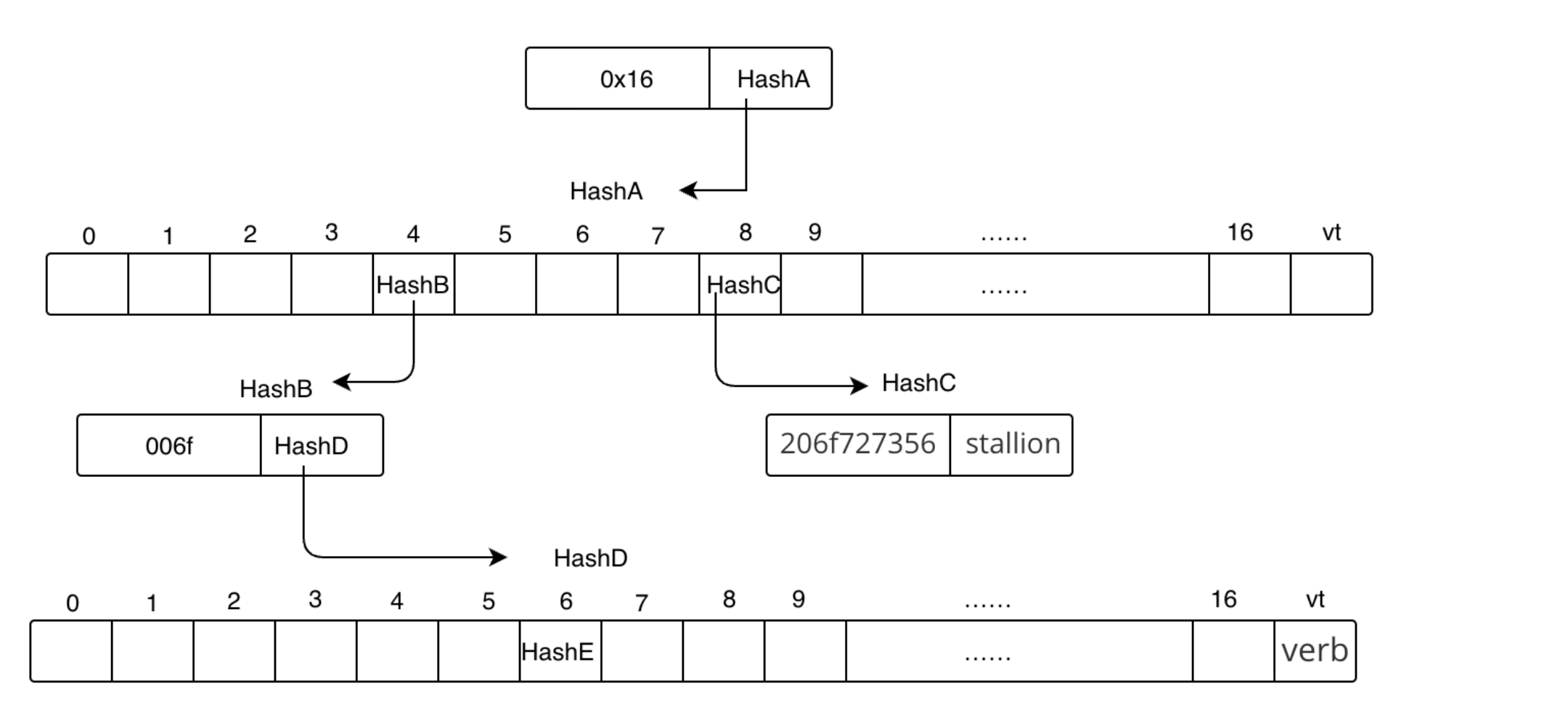
6.
<64 6f> : 'verb'
<64 6f 67> : 'puppy'
<64 6f 67 65> : 'coin'
<68 6f 72 73 65> : 'stallion'
接下来是共同路径7,一个extension节点,开始计算HP编码,7长度是奇数,又是extension类型,所以HP前缀为0x1,HP编码为0x17。
所以当前默克尔树如下图:
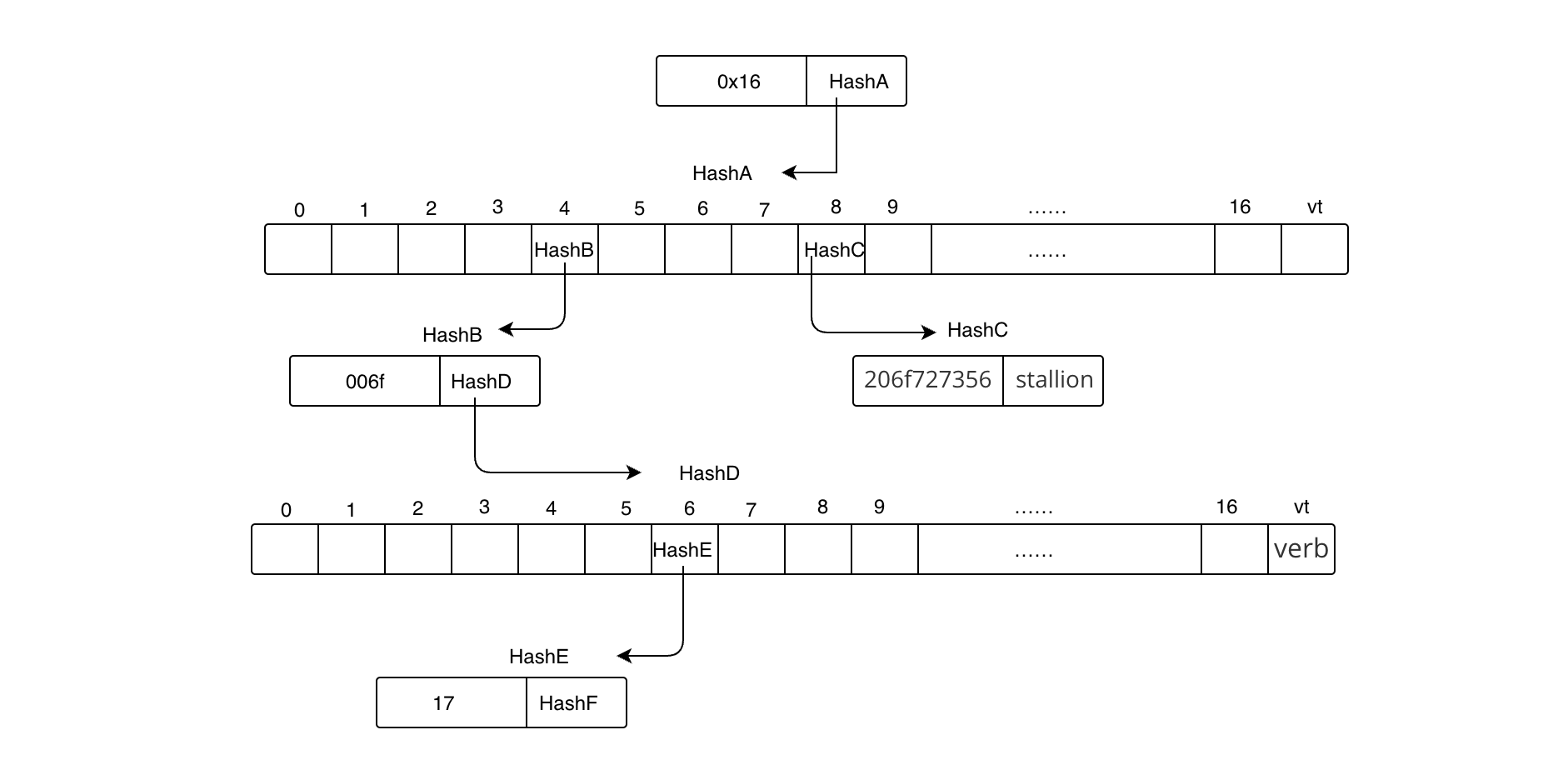
8.
<64 6f> : 'verb'
<64 6f 67> : 'puppy'
<64 6f 67 65> : 'coin'
<68 6f 72 73 65> : 'stallion'
7后分出了null和6,是多条路径,与第五步相同,HashF是一个branch节点,索引为6的元素存储子节点哈希,vt存储'puppy'的值
所以当前默克尔树如下图:
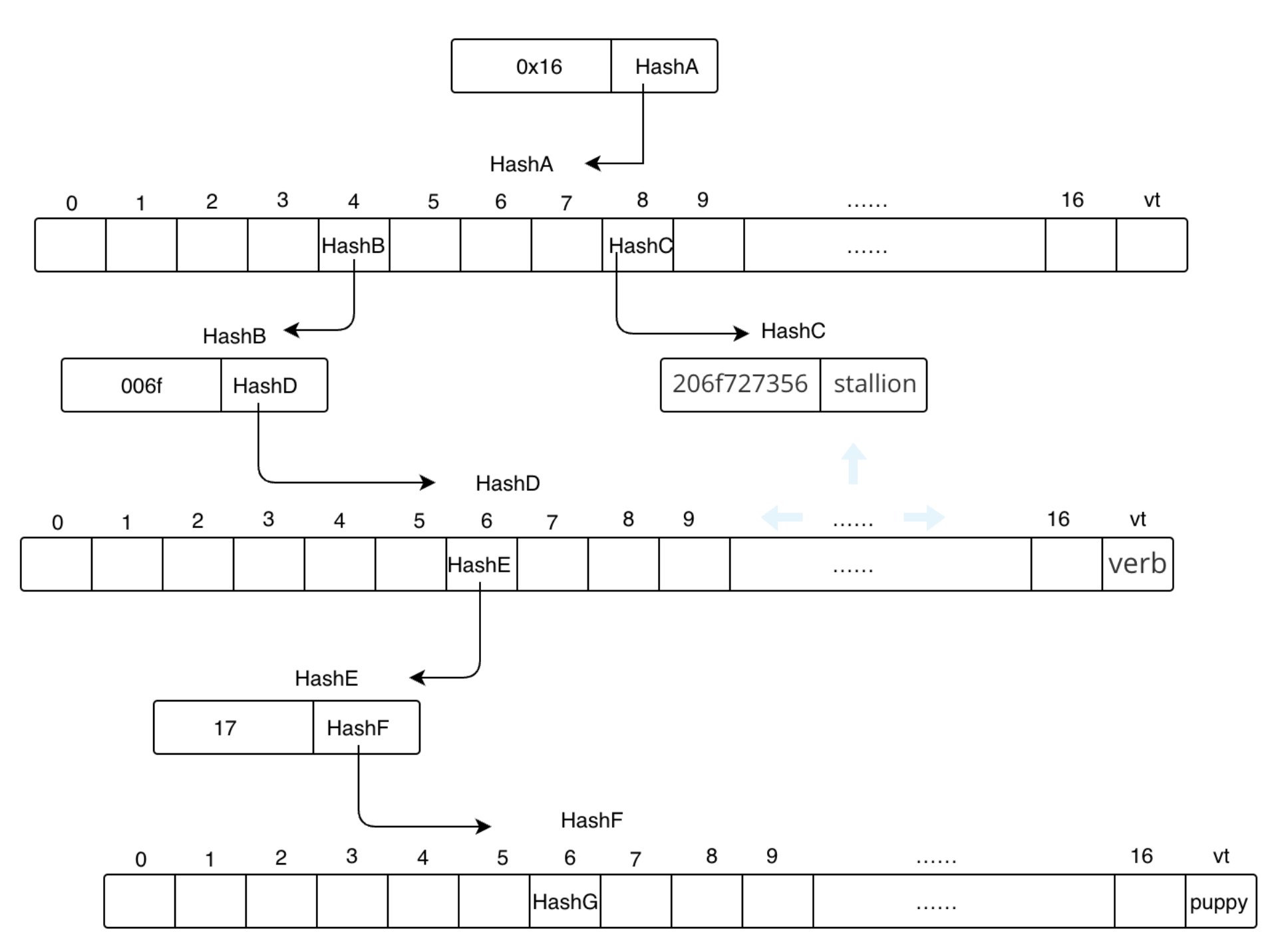
9.
<64 6f> : 'verb'
<64 6f 67> : 'puppy'
<64 6f 67 65> : 'coin'
<68 6f 72 73 65> : 'stallion'
好了,现在只剩下一条路径了,表示这最后一个是一个leaf叶子节点,路径为5,路径长度为奇数,索引HP前缀为0x3,HP编码为0x35
所以当前也是最终的默克尔树如下图:
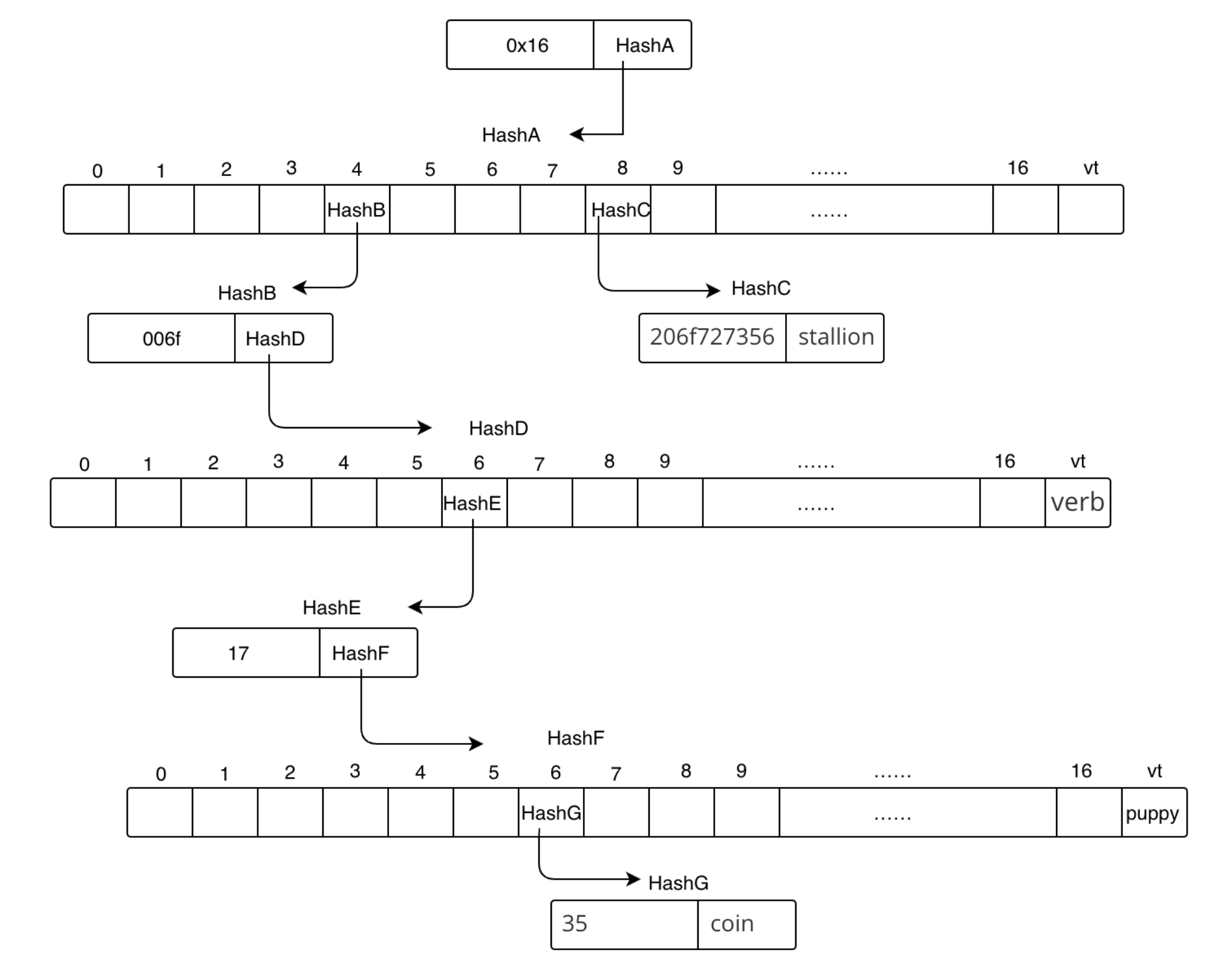
以上就是这棵默克尔树构造的全部过程了,写得很详细,是希望能够为在阅读书籍时没有理顺思路的小伙伴们提供一些帮助。
三、总结
从构造过程中我们可以看出,MPT中节点之间,是通过哈希值来确定的。由于哈希值的特性,只要数据有了微小改动,就会导致根节点改变,所以我们可以用树的根节点来代表整个树中数据的状态,这样就不用保存整个树的数据。
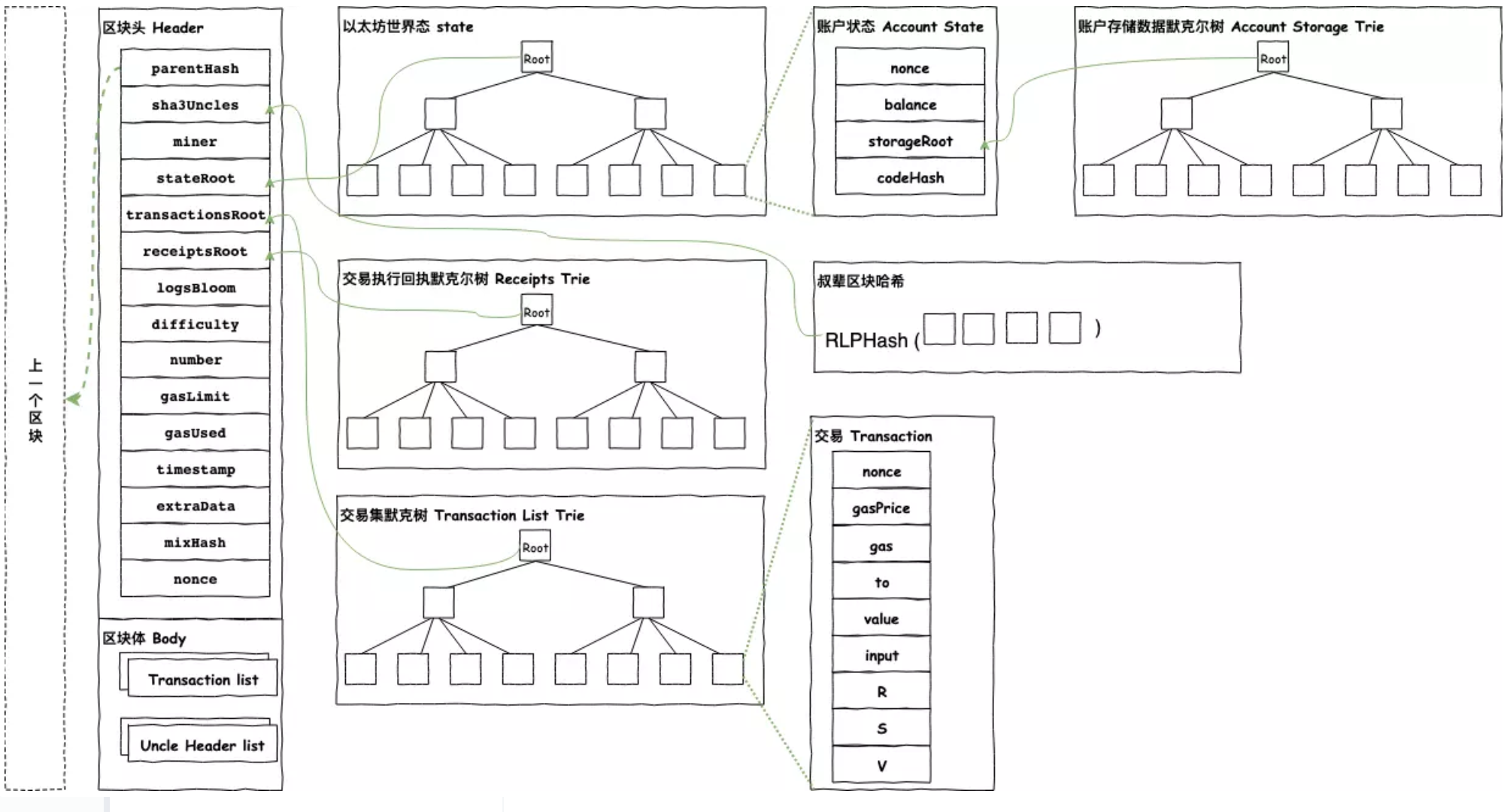
在以太坊中,默克尔树有着大量的应用,比如保存和验证系统中的所有账户状态、所有合约的存储状态、区块中的所有交易和所有收据数据的状态等。
参考
《深入以太坊智能合约开发》
- 基于哈希函数的签名(四):XMSS 和 SPHINCS 560 浏览
- 基于哈希函数的签名(三):多次签名 722 浏览
- 64 字节长的比特币交易 1206 浏览
- 区块链密码学基础概念 2501 浏览
- 用于验证 Taproot 资产转移的虚拟机执行环境 1550 浏览
- Merkle Patricia Trie 简介 1589 浏览
- 不可重用证明1 961 浏览
- bips/bip-tap-proof-file.mediawiki,位于 bip-tap · Roasbeef/bips 1327 浏览
- 空投大杂烩 - 合约实现空投发放的三种方案 3460 浏览
- ariard/bips 的bips/bip-merklesub.mediawiki,提交版本号为ddb77158a8309f307faaaf643830e4d0f07b90d3 1667 浏览
- bips/bip-tap-universe.mediawiki,位于 Roasbeef/bips 的 Taproot 资产宇宙 1130 浏览
- 比特币 - bips/bip-tap-ms-smt.mediawiki,位于Roasbeef/bips - Roasbeef 1109 浏览

