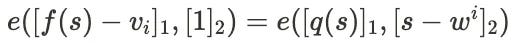以太坊无状态系列 #3：Verkle 树验证
- Chaisomsri
- 更新于 3天前
- 阅读 91
以太坊无状的一个关键是，让证明数据足够小
1. 引入 Verkle 树的原因
Vitalik 在“A state expiry and statelessness roadmap”中提出了实现无状态性的两种方法：
- 状态到期
- 弱无状态
状态到期和弱无状态在第一部分中有详细介绍。简要回顾一下，弱无状态只需要区块提议者存储状态，允许验证状态的节点无需自行存储状态。如果区块提议者提交一个证明，指示特定值是否包含在特定位置，验证节点就无需存储状态。
减少证明的大小对于弱无状态至关重要。这是因为每次生成区块时都必须创建和传输一个证明。当前默克尔树创建的证明大小会随着树的深度和广度的增加而增加，这使其不合适。Verkle 树可以创建恒定大小的证明，是一个值得采用的有前途的候选者。
2. 为什么需要树的证明？
证明是指示特定值是否包含在特定位置的证据。引入 Verkle 树以减少状态到期的证明大小突显了证明的重要性。那么，这是否意味着以太坊不需要概念证明，因为完整节点存储整个状态？
以太坊节点可以分为三种类型：存档节点、完整节点和轻节点。存档节点存储所有数据。完整节点从创世区块开始拥有所有数据，但不保留历史状态，尽管它们可以提供当前状态。轻节点只有区块头。
轻节点无法向其他节点或客户端提供数据，必须从完整节点接收证明以验证其接收的数据是否正确。轻节点使用证明和它们拥有的区块头中的状态根来验证数据。
因此，存档节点和完整节点不需要证明。这些节点可以验证它们收到的请求，因为它们拥有数据。证明是为轻节点准备的，它们无法独立验证收到的请求。
然而，证明对以太坊的用户至关重要。 让我们考虑在 Devcon 6 上介绍的一个示例。
来源：Light Clients After the Merge by Etan Kissling | Devcon Bogota
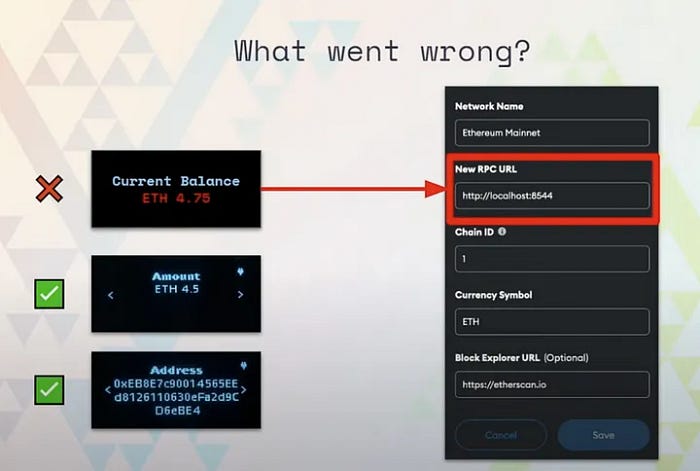
MetaMask，一个广泛使用的钱包之一，需要输入由主网节点提供的 RPC URL，以向主网发送请求。如果用户没有运行自己的完整节点，则必须使用其他人提供的节点 URL。但如果信任的节点被证明是恶意的呢？
来源：Light Clients After the Merge by Etan Kissling | Devcon Bogota
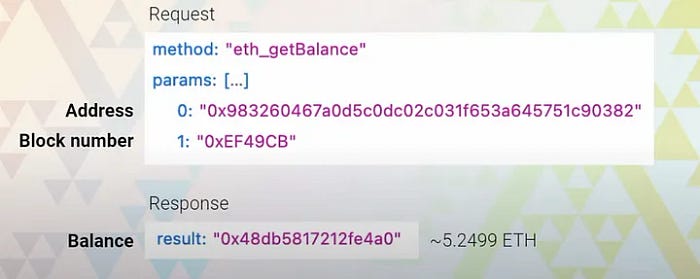
MetaMask 不会独立验证其检索到的数据。 它查询节点 RPC URL 以获取当前登录到钱包的地址的以太和代币余额的信息。因此，如果节点故意报告不正确的以太数量，MetaMask 无法检测到这一点，并将信息如实显示给用户。 例如，即使用户在交易中发送了 1 以太，节点也可能错误地报告以太余额没有减少，导致用户认为交易失败，并可能发送另外 1 以太。
来源：Light Clients After the Merge by Etan Kissling | Devcon Bogota
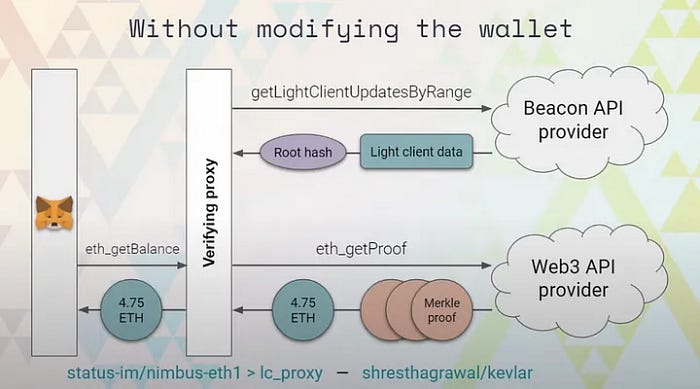
为了安全使用 MetaMask，建议使用一个代理在 MetaMask 前面检索和验证证明。即使节点提供不正确的数据，有了证明也可以验证这些数据。
因此，证明不仅对轻节点重要，而且对最终用户也起着至关重要的作用。
3. Merkle 树的验证方法
来源：merkle-proofs-for-offline-data-integrity
树是可以存储数据的数据结构。树的顶部节点称为根节点，具有子节点的节点称为内部节点，没有子节点的节点称为叶节点。
Merkle 树将数据存储在叶节点中，内部节点包含通过将子节点输入哈希函数而获得的值。在树中包含哈希值而不仅仅是数据的原因是为了生成证明。
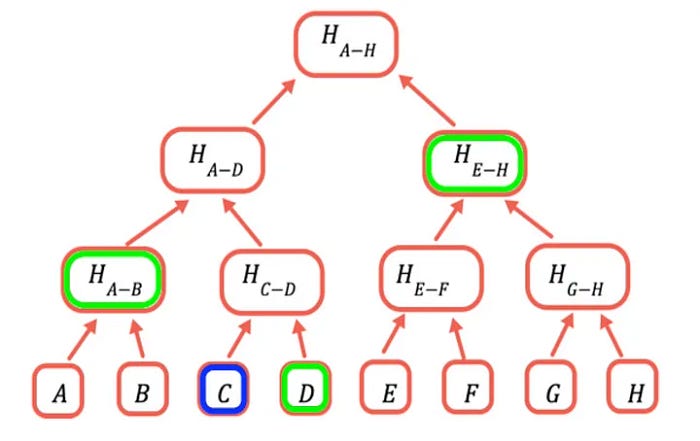
如果以太坊的状态存储在 Merkle 树中，轻节点可以通过仅拥有根节点的值（Merkle 根）和通过证明来知道特定值是否存在于 Merkle 树中。
例如，为了证明上图中 C 存在于 Merkle 树中，轻节点需要提交 D、H(A-B)和 H(E-H)作为证明。轻节点可以使用 C 和接收到的 D 作为证明计算 H(C-D)，然后使用 H(C-D)和接收到的 H(A-B)作为证明计算 H(A-D)。最后，通过使用 H(E-H)和 H(A-B)作为输入计算哈希值，并将其与他们拥有的 Merkle 根进行比较，他们可以验证 C 是否存在于 Merkle 树中。
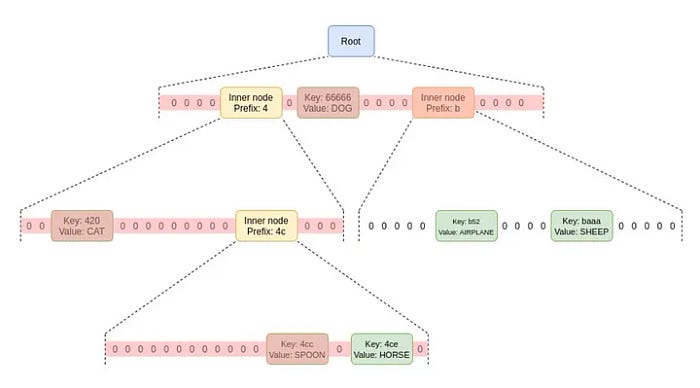
以太坊使用 Merkle Patricia 树，它同时满足 Merkle 树和 Patricia 树的属性。Patricia 树是一种使用作为键的字符串的前缀来组织内部和叶节点的树。使用 Patricia 树的优点是在根据特定键添加或删除数据时不需要移动所有节点以维护树的顺序。
以太坊使用的是十六制（hexary） Merkle Patricia 树，与示例不同，最多有 16 个子节点。Vitalik 在他的著作中指出，当 Merkle 树具有两个子节点时效率最高。
然而，以太坊使用 16 个子节点，因为它在树中存储“状态”。以太坊有一个树，其中键是地址，值是余额、nonce、代码等。这种树的问题在于与地址关联的余额和 nonce 等值会发生变化，并且随着用户涌入会生成新地址。也就是说，修改和插入频繁发生，因此需要减少这些成本。因此，以太坊通过在 hexary 树中编码键进行了优化，导致有 16 个子节点。有关优化的详细信息超出了本文的范围，但感兴趣的人可以参考以下文章 。
hexary Merkle Patricia 树的缺点是证明的大小很大。在生成证明时，必须包含同一高度的所有兄弟节点。而二叉树只有一个兄弟节点，hexary 树有 15 个，使得大小大得多。通过消除状态以引入无状态性，意味着证明的大小成为一个重要障碍。Verkle trees 提供了与默克尔树相同的功能，同时解决了证明大小的问题。在接下来的段落中，我们将探讨 Verkle 树如何验证和减小证明的大小。
4. Verkle 树的证明
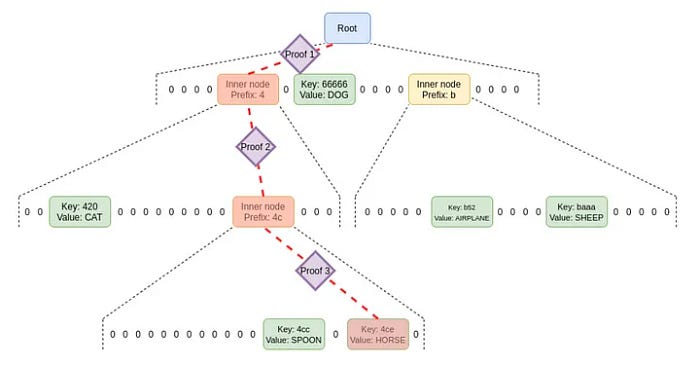
Verkle 树与 Merkle 树的不同之处在于证明的大小是恒定的。这是因为在证明中不需要包含兄弟节点。
在 Merkle 树中，为了证明键为 4ce 的值 HORSE 的存在，内部节点必须包含它们的哈希值以及所有子节点（用红色标记）。
然而，Verkle 树不是这样操作的。Verkle 树通过使用向量承诺来解决证明大小问题。简单来说，向量承诺方案是一种特殊类型的哈希函数。在 Verkle 树中，每个级别的证明大小与兄弟节点的数量无关，这使得增加宽度变得更容易。事实上，关于设置宽度在 256 和 1024 之间的讨论正在进行中。
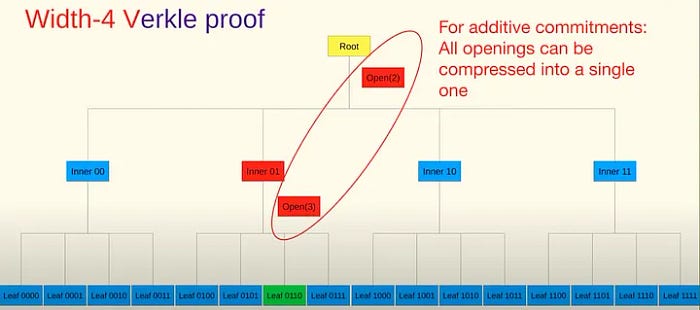
Verkle 证明。来源：Verkle tries for Ethereum state with Dankrad Feist
Merkle 树在内部节点存储值以进行存在性证明。Verkle 树也在内部节点中存储值，称为承诺。与 Merkle 树不同，承诺不仅仅是通过哈希获得的，而是需要子节点的值。承诺如何计算会改变 Verkle 树的验证方法，因为承诺会影响证明的创建。
在 Verkle 树中生成证明的公式称为Opening。一个 Opening，Open(C, x, i, v)，证明了当承诺为 C 时，x_i = v。
通过 Openings 生成的证明可以压缩成一个。因此，不是每个级别都有一个证明，总共有 log(n)个证明，而是最终可以压缩成一个单一的证明，实现大小为 O(1)。
无论子节点的数量如何，证明的大小如何保持恒定呢？要完全理解这一点需要具备高级数学知识。然而，本文将避免深入的数学证明，以便更容易理解整体情况。首先，我们将看一下早期讨论中提到的KZG 承诺，然后我们将探讨当前被认为是一个有前途的采用选项的Pedersen 承诺。
5. Verkle 树的验证方法 — KZG 承诺
考虑一个最多有 d 个子节点的 d 元 Verkle 树。每个内部节点都保存通过其子节点计算的承诺，并且可以生成证明以证明特定子节点的存在。
KZG 承诺使用多项式来创建承诺。 使用多项式创建承诺的过程如下：
- 选择一个 w，使得 w^d = 1，并且对于 0≤i<d，w^i≠1。
- 使用拉格朗日插值来唯一定义一个次数为 d-1 的多项式 f，使得对于 0≤i<d，f(w^i)=v_i。
- 通过将一个特定值 s代入 f 来计算 f(s)。
- 将 f(s)映射到椭圆曲线以计算[f(s)]（椭圆曲线的解释查看 Vitalik Buterin 的著作）。
- 使用[f(s)]作为承诺。
这意味着使用第 i 个子节点的值 v_i 创建一个多项式 f，并使用它来计算承诺。有一个前提条件，即用于创建承诺的值 s 必须对任何人都是未知的。如果 s 被泄露，就有可能创建一个不同的多项式 f’(x) = f(x)-x+s，但具有相同的承诺。因此，伪造子节点的值并创建证明其存在是可能的，因此 s 绝不能被披露。
当 f(w^i) = v_i 时，证明为[(f(s)-v_i)/(s-w^i)]。进一步解释，由于 f(w^i) = v_i 被认为是成立的，q(x) = {f(x)-v_i}/(x-w^i)也是一个多项式。这个多项式就是 Opening，通过将 s 代入 Opening 得到的值就是 Proof，即证明是 q(s)。通过这种方式计算证明满足以下方程：
这里，e 代表椭圆曲线上的配对概念。
这个方程意味着什么？假设我们是持有 Verkle 树的一个节点。我们知道承诺，即 f(s)。一个用户声称内部节点的第 i 个子节点的值是 v_i，并提交了一个证明。我们已经知道 f(s)，并且从用户那里收到了 v_i、w^i 和证明[[q(s)]，使我们了解方程式的所有元素。现在我们可以直接计算以检查等式是否成立。如果成立，就确认第 i 个子节点的值确实是用户声称的 v_i。
总之，Verkle 树的每一层都有一个承诺，并提交相应的证明可以验证子节点值的存在。
然而，这并不满足无状态性的条件，这要求证明的大小是恒定的。由于每一层都需要一个证明，总共需要 O(logn)个证明。为了实现恒定大小，这些证明必须再次被压缩。 简化来说，上面看到的方法被扩展以创建用于证明的多项式。有关详细解释，请参考 Dankrad Feist 的文章 （PCS 多证明）。
如果你迄今为止一直在关注，你应该大致了解了 KZG 承诺如何用于将 Verkle 树证明的大小减小到一个恒定值。然而，KZG 承诺方法有一个关键缺点：创建一个未知的 s 非常具有挑战性。 知道 s 的攻击者可以创建一个伪造的开启以证明一个不存在的值的存在。 下一节将探讨 Pedersen 向量承诺，它不使用 s。
6. Verkle 树的验证方法 — Pedersen 向量承诺
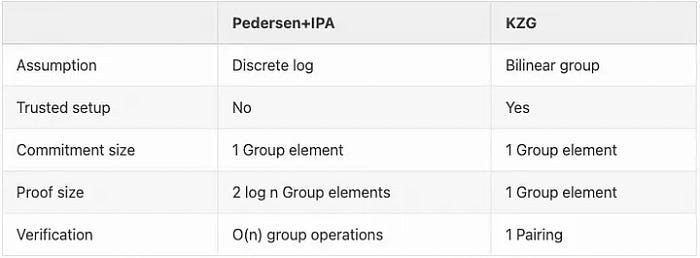
Pedersen 向量承诺（以下简称 Pedersen）是一种创建承诺的方案。内积论证（IPA）是在 Pedersen 之上创建开启的方案。通过将 Pedersen 和 IPA 结合使用，可以创建证明，而无需像 KZG 那样需要一个可信的设置。
如上表所示，缺点是证明的大小增加，验证时间变长。 尽管由于其对数尺度，证明的大小可能是可以管理的，但验证时间的线性增加对于应用程序可能是关键的。
为了减轻这一劣势，使用了 多证明压缩 和前面简要提到的Halo协议。 (1) 将多个证明合并为一个证明和 (2) 使用 Halo 允许在较短时间内验证组合开启。Halo 协议将验证步骤分为 k 部分，在每一步创建和组合证明，从而允许在几乎 O(k)时间内进行验证。应用 Halo 到 IPA 显示，尽管证明比 KZG 的大，但验证时间缩短到一个常数。因此，它适用于 Verkle 树的应用，因为它不需要可信设置，同时保持证明大小小，减少验证时间。
Verge 路线图。来源：Vitalik Twitter
Halo 是应用于 Zcash 的协议，并且基于与 SNARK 链合作。这意味着，必须是基于 IPA 的 SNARK 块才能应用 Halo。事实上，看看 Verge 的路线图，最终目标是一个完全基于 SNARK 的以太坊。为 SNARKs 创建 Verkle 证明可以减少证明大小和验证时间，为无状态性做准备。
想要了解 Pedersen、IPA 和 Halo 操作的人，请参考 Dankrad Feist 和 Vitalik Buterin 的文章。
7. 结论
Verkle 树旨在减少证明（见证）的大小，以证明树中特定位置的特定值的存在/不存在所需。随着无状态性的应用，这是至关重要的，因为节点和用户将频繁交换见证人。有各种方法可以实现 Verkle 树，Pedersen 向量承诺方法是一种有前途的方法。
本文简要介绍了引入 Verkle 树及其验证方法的原因。在下一篇文章中，我们将看看 Merkle 树和 Verkle 树的结构有何不同。
