也许是国内第一篇把以太坊工作量证明从算法层讲清楚的
- 七哥
- 发布于 2020-04-23 15:17
- 阅读 11927
找遍中文资料,没有哪篇文章能对以太坊工作量证明有一个全面的介绍。对于没有把数学学会的同学来说,如果希望从算法层了解以太坊的工作量证明是非常困难的。一本黄皮书会难倒一大批吃瓜群众。因此,本文将试图使用图文和尽量简单的数学来解释以太坊挖矿工作量证明,包括以太坊是如何对抗ASIC1、如何动态调整挖矿难度、如何校验挖矿正确性的。
对于没有把数学学会的同学来说,如果希望从算法层了解以太坊的工作量证明是非常困难的。一本黄皮书会难倒一大批吃瓜群众。因此,本文将试图使用图文和尽量简单的数学来解释以太坊挖矿工作量证明,包括以太坊是如何对抗ASIC1、如何动态调整挖矿难度、如何校验挖矿正确性的。
认识工作量证明PoW
工作量证明(Proof-of-Work,PoW)是一种对应服务与资源滥用、或是拒绝服务攻击的经济对策。 一般是要求用户进行一些耗时适当的复杂运算,并且答案能被服务方快速验算,以此耗用的时间、设备与能源做为担保成本,以确保服务与资源是被真正的需求所使用。
摘自维基百科
这种经济性应对政策概念,是在1993年提,直到1999年才使用 Proof-of-Work一词。
Proof of Work ,直接翻译过来是工作量证明。这个词的中文直接听起来有点不知所云。实际上如果我跟你说结婚证明,离职证明,那你是不是首先想到的是一张上面印着一些东西的纸呢?别人看到这张纸就知道你的确结婚了,或者你的确从某单位离职了。工作量证明从语法上也是一个逻辑,也可以理解成一张纸,通过这张纸就可以证明你的确完成了一定量的工作。这就是工作量证明的字面意思。
那工作量证明有什么特点呢?我们抛开计算机,用现实世界的例子来说明。例如我上课不认真,老师罚我把《桃花源记》抄写十遍,我用了两个小时的劳动,最后给老师的就是一张纸,而老师要确认我的确付出了大量劳动,其实只需要看一眼就可以了。这个例子道出了 POW 机制的一大特点,那就是生成需要花费大量劳动,但是验证只需一瞬间。另外一个工作量证明的例子可以是,老师给我出一道题,我给老师的运算结果,或者说就是最后的那个数字,就是我的工作量证明。回到计算机情形下,纸当然是不存在的,所以所谓的工作量证明就是花费了很多劳动而得到的一个数了。
再说说 POW 最早的用途。人们在使用电子邮件的时候会收到垃圾邮件的骚扰。如果没有成本,那么发送一百万封邮件的确是很轻松的事情了。所以,聪明的人就会想,如果让每一封邮件发送时候,都有一个微小的成本,那么垃圾邮件就会被很大程度的遏制了。而 POW 就是为了服务这个目的产生的。基本过程就是邮件接收方会先广播一道题出去,邮件发送方发邮件的时候必须附带上这道题的答案,这样邮件才会被接受,否则就会被认为是垃圾邮件。
挖矿
挖矿就是在求解一道数学方程。方程的多个可能的解被称为解的空间。挖矿就是从中寻找一个解。 不同于几何方程,这个挖矿方程有如下特点:
- 没有比穷举法更有效的求解方法;
- 解在空间中均匀分布,每一次穷举查找到解的概率基本一致;
- 解的空间足够大,保证一定能够找到解;
假设挖矿方程是: n=random(1,10),求 n< D。
当 D为10时,我们只需要运算一次就可以找到任意的n都满足 n<10,可当 D =5,则平均需要两次运算才能找到 n<5,随着D的减小,需要运算的次数就会增大。
这里的D 就是通常说的挖矿难度,通过调整解空间中的符合要求的解的数量来控制求解所需要尝试的次数,间接的控制产生一个区块所需要的时间。使得可以调控和稳定区块间隔时间。
当挖矿的人很多,单位时间内尝试次数增多时,求解的速度也就更快,区块挖出用时更短。此时则增大挖矿难度,增大平均尝试次数,使得挖矿耗时上升。反之依然。
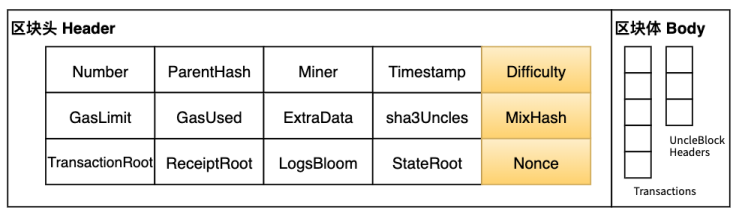
以太坊新区块挖矿流程
通过父区块可计算新区块的挖矿难度,再求解挖矿方程。
挖矿工作量证明通过一个密码学安全的nonce来证明“为了获得挖矿方程解n,已经付出了一定量的计算”。工作量证明函数可以用PoW表示:
$$
m = H_{m} \; \wedge \;
n \leq \frac{2^{256} } {Hd} \qquad
\text{with} \quad (m,n) = \text{PoW}(H{\cancel{nm} },H_{n},\textup{d})
$$
 其中
其中
- $H_{\cancel{nm}}$ 是新的区块头,但nonce和mixHash均为空值;
- $H_d$ 是区块 difficulty 值。;
- $H_m$ 是区块mixHash值;挖矿方程算法返还的第一个参数值;
- $H_n$ 是区块nonce值; 挖矿方程算法返还的第二个参数值;
- $d$ 是一个计算mixHash所需要的大型数据集dataset;
- PoW是工作量证明函数,可以得到两个值,其中第一个是mixHash,第二个是密码学依赖于 H和d的伪随机数。
这个基础算法就是挖矿方程Ethash。通过可以信任的挖矿方程求解,来确保区块链的安全性。同时,挖出新块还伴有区块奖励,所以工作量证明不仅提供安全保障,还是一个利益分配机制。
下面是挖矿工作量证明的计算过程:

大致流程如下:
- 根据父区块头和新区块头计算出$H_d$ ;
- 在PoW开始时选择一个随机数作为Nonce的初始化值;
- 将Nonce和作为挖矿方程Ethash的入参;
- 执行Ethash将得到两个返回值:mixHash和 result;
- 判断 result 是否高于 Traget( 2256/$H_d$ ) 。如果是则 nonce加1,继续穷举查找; 否则,如果是则说明求解成功。返回 mixHash和Nonce;
- 两个值记录到区块头中,完成挖矿。
区块难度 difficulty
以太坊的挖矿难度记录在区块头difficulty上 ,那么在它是如何动态调整的呢?
调整算法在以太坊主网有多次修改,即使以太坊黄皮书中的定义也和实际实现代码也不一致,这里我以程序实现代码来讲解区块难度调整算法。
$$
H{i}^D=\begin{cases}
H{0}^D & \text{if} \; H_{i}=0 \
\text{max}(H0^D, H{i-1}^D + x \times \zeta_{2} + \epsilon ) & \text{otherwise} \
\end{cases}
$$
其中有: $$ H{0}^D= 131,072 \ x = \frac{ H{i-1}^D}{2048} \ \zeta{2} = \text{max}( y - \frac{ H{i}^T - H{i-1}^T }{9} ,-99 ) \ y =\begin{cases} 1 & \text{if} \; H{i-1}^U =0\ 2 & \text{otherwise} \ \end{cases} \ \epsilon = 2^{ \frac{ \text{max}(H_i-H_i^{'},0) }{100000} -2} \ H_i^{'}= 5,000,000 $$
$H{0}^D$是创世区块的难度值。难度值参数 $\zeta{2} $被用来影响出块时间的动态平衡。使用了变量而非直接使用两个区块间的时间间隔,是用于保持算法的粗颗粒度,防止当区块时间间隔为1秒时只有稍微高难度情况。也可以确保该情况下容易导致到软分叉。
-99 的上限只是用来防止客户端安全错误或者其他黑天鹅问题导致两个区块间在时间上相距太远,难度值也不会下降得太多。在数学理论是两个区块的时间间隔不会超过24秒。
难度增量 $\epsilon$ 会越来越快地使难度值缓慢增长(每10万个区块),从而增加区块时间差别,为以太坊2.0的权益证明(proof-of-stake)切换增加了时间压力。这个效果就是所谓的“难度炸弹”(“difcultybomb”)或“冰河时期”(“iceage”)。
以太坊的设想是最终从PoW过度到PoS,为了给过度施加时间压力,所以在区块难度中预埋了一个难度炸弹 $\epsilon$ ,他是以2的指数级增长的。如果听过“棋牌摆米”的数学故事,就应该清楚指数级增长是非常恐怖的。
最终,在拜占庭版本中,伴随EIP-649,通过伪造一个区块号 $H_i^{'}$ 来延迟冰河时期的来临。这是通过用实际区块号减去300万来获得的。换句话说,就是减少 $\epsilon$和区块间的时间间隔,来为权益证明的开发争取更多的时间并防止网络被“冻结”。
在君士坦丁堡版本升级中,以太坊开发者在视频会议中表示,如果直接执行难度炸弹,那么难保以太坊能顺利切换到PoS就有大量矿工离开,这很有可能极大的影响以太坊的安全性。因此,伴随EIP-1234,再一次修改 $H_i^{'}$ 到500万来延迟冰河时期。
这个挖矿难度调整机制保证了区块时间的动态平衡;如果最近的两个区块间隔较短,则会导致难度值增加,因此需要额外的计算量,大概率会延长下个区块的出块时间。相反,如果最近的两个区块间隔过长,难度值和下一个区块的预期出块时间也会变短。
挖矿方程Ethash
区块链鼻祖比特币,是PoW共识,已经稳定运行10年。但在2011年开始,因为比特币有利可图,市场上出现了专业矿机专门针对哈希算法、散热、耗能进行优化,这脱离了比特币网络节点运行在成千上万的普通计算机中并公平参与挖矿的初衷。这容易造成节点中心化,面临51%攻击风险。因此,以太坊需要预防和改进PoW。因此在以太坊设计共识算法时,期望达到两个目的:
- 抗ASIC1性:为算法创建专用硬件的优势应尽可能小,理想情况是即使开发出专有的集成电路,加速能力也足够小。以便普通计算机上的用户仍然可以获得微不足道的利润。
- 轻客户端可验证性: 一个区块应能被轻客户端快速有效校验。
在以太坊早期起草的共识算法是 Dagger-Hashimoto,由 Buterin和 Dryja提出。 但被证明很容易受到 Sergio Lerner 共享内存硬件加速的影响。 所以最终抛弃了 Dagger-Hashimoto,改变研究方向。 在对 Dagger-Hashimoto 进行大量修改,终于形成了明显不同于 Dagger-Hashimoto 的新算法:Ethash。Ethash 就是以太坊1.0 的挖矿方程。
介绍
这个算法的大致流程如下:
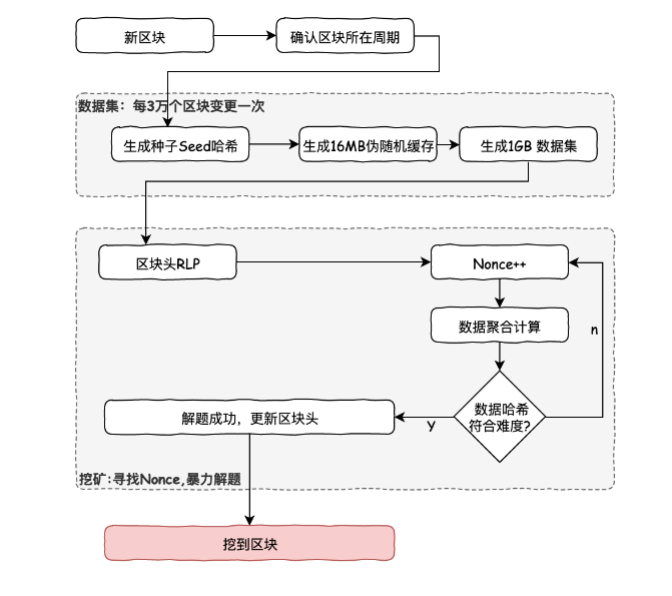
- 通过扫描区块头直到某点,来为每个区块计算得到一个种子 Seed。
- 根据种子可以计算一个初始大小为 16MB的伪随机缓存cache。轻客户端保存这个 cache,用于辅助校验区块和生成数据集。
- 根据 cache, 可以生成一个初始大小为 1GB的DAG数据集。 数据集中的每个条目(64字节)仅依赖于 cache 中的一小部分条目。数据集会随时间线性增长,每30000个区块间隔更新一次。 数据集仅仅存储在完整客户端和矿工节点,但大多数时间矿工的工作是读取这个数据集,而不是改变它。
- 挖矿则是在数据集中选取随机的部分并将他们一起哈希。 可以根据 cache 仅生成验证所需的部分,这样就可以使用少量内存完整验证,所以对于验证来讲,仅需要保存 cache 即可。
这里cache选择16 MB 缓存是因为较小的高速缓存允许使用光评估(light-evaluation)方法,太容易用于 ASIC。 16 MB 缓存仍然需要非常高的缓存读取带宽,而较小的高速缓存可以更容易地被优化。 较大的缓存会导致算法太难而使得轻客户端无法进行区块校验。
选择初始大小为 1GB 的DAG数据集是为了要求内存级别超过大多数专用内存和缓存的大小,但普通计算机能够也还能使用它。 数据集选择 30000 个块更新一次,是因为间隔太大使得更容易创建被设计为非常不频繁地更新并且仅经常读取的内存。 而间隔太短,会增加进入壁垒,因为弱机器需要花费大量时间在更新数据集的固定成本上。
同时,缓存和数据集大小随时间线性增长,且为了降低循环行为时的偶然规律性风险,数据大小是一个不超过上限的素数。 每年约以0.73倍的速度增长,这个增长速率大致同摩尔定律持平。这仍有越过摩尔定律的风险,将导致挖矿需要非常大量的内存,使得普通的GPU不再能用于挖矿。因为可通过使用缓存重新生成所需数据集的特定部分,少量内存进行PoW验证,因此你只需要存储缓存,而不需要存储数据集。
缓存和数据集大小
缓存c和数据集d的大小依赖用区块的窗口周期Eepoch。 $$ E_{epoch}= \frac{H_i}{30000} $$
每过一个窗口周期后,数据集固定增长8MB(223 字节),缓存固定增长 128kb(217 字节)。为了降低循环行为时的偶然规律性风险,数据大小必须是一个素数。
计算缓存大小公式:
$$
c{size}= E{prime}( 16\text{MB} + 128\text{KB} \cdot E{epoch} - 64\text{bytes}, 64\text{bytes} )
$$
计算数据大小公式:
$$
d{size}= E{prime}( 1\text{GB} + 8\text{MB} \cdot E{epoch} - 64\text{bytes}, 64\text{bytes} )
$$
其中,求素数公式如下:
$$
E{prime(x,y)}=\begin{cases}
x & \text{if} \;\; x/y \in \mathbb{ P} \
E{prime(x-2 \cdot y,y)} & \text{otherwise} \
\end{cases} \
$$
这个素数计算是从不高于上限值中向下依次递减2*64字节递归查找,直到 x/64是一个素数。
生成种子哈希值
种子seed实际是一个哈希值,每个窗口周期(30000个区块)更新一次。它是经过多次叠加Keccak256计算得到的。
第一个窗口周期内的种子哈希值s 是一个空的32字节数组,而后续每个周期中的种子哈希值,则对上一个周期的种子哈希值再次进行Keccak256哈希得到。

生成缓存cache
缓存cache 生成过程中,是将cache切割成64字节长的若干行数组操作的。
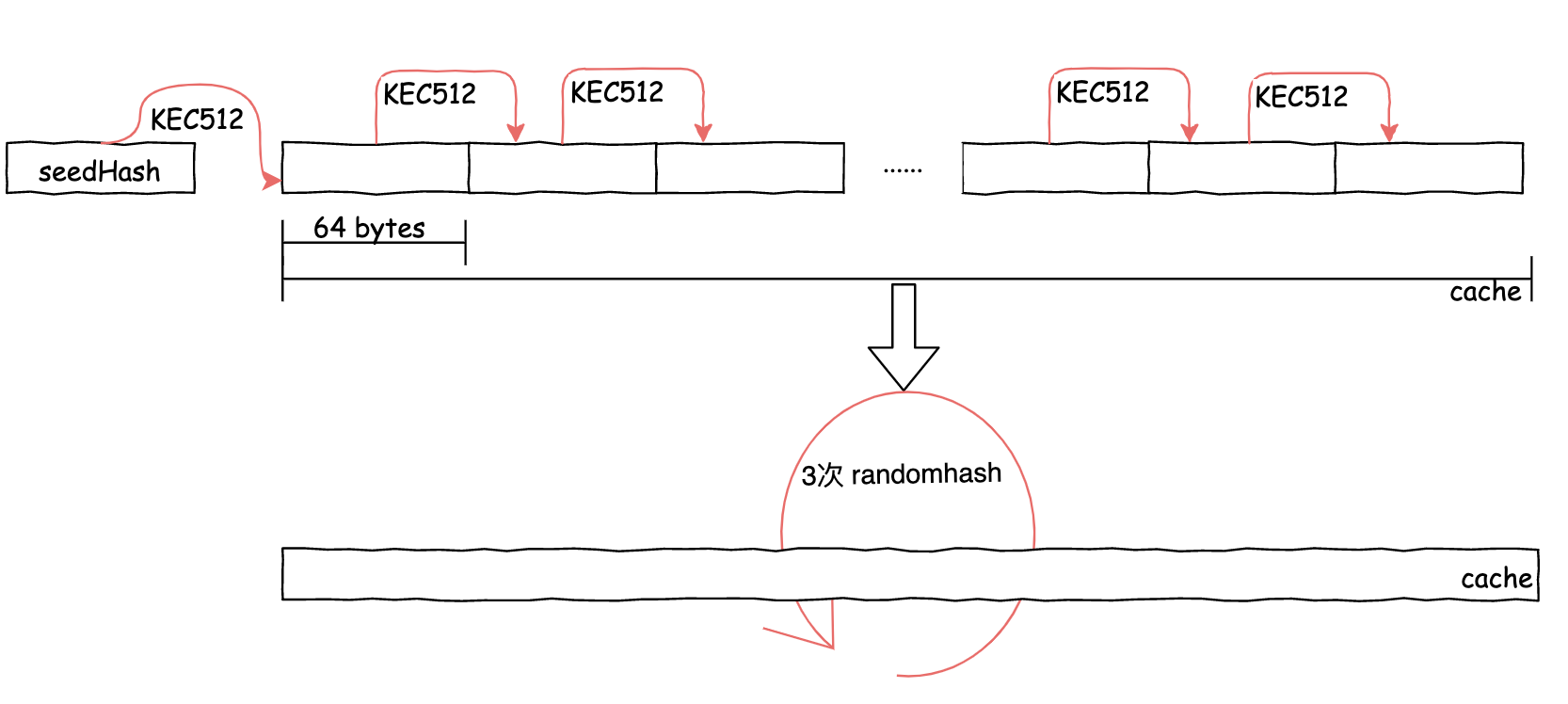
先将种子哈希值的Keccak512结果作为初始化值写入第一行中;随后,每行的数据用上行数据的Keccak512哈希值填充;最后,执行了3次 RandMemoHash算法(在严格内存硬哈希函数 Strict Memory Hard Hashing Functions (2014)中定义的内存难题算法)。该生成算法的目的是为了证明这一刻确实使用了指定量的内存进行计算。
RandMemoHash 算法可以理解为将若干行进行首尾连接的环链,其中n为行数。
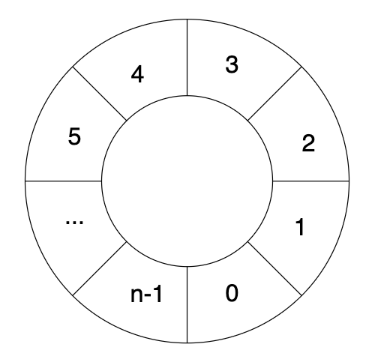
每次RandMemoHash 计算是依次对每行进行重新填充。先求第 i 行的前后两行值得或运算结果,再对结果进行Keccak512哈希后填充到第i行中。
最后,如果操作系统是 Big-Endian(非little-endian)的字节序,那么意味着低位字节排放在内存的高端,高位字节排放在内存的低端。此时,将缓存内容进行倒排,以便调整内存存放顺序。最终使得缓存数据在内存中排序顺序和机器字节顺序一致。
生成数据集
利用缓存cache来生成数据集,首先将缓存切割成n个16 bytes大小的单元。在生成过程中时将数据集切割为若干个64bytes大小的数据项,可对每项数据mix并发生成。最终将所有数据项拼接成数据集。
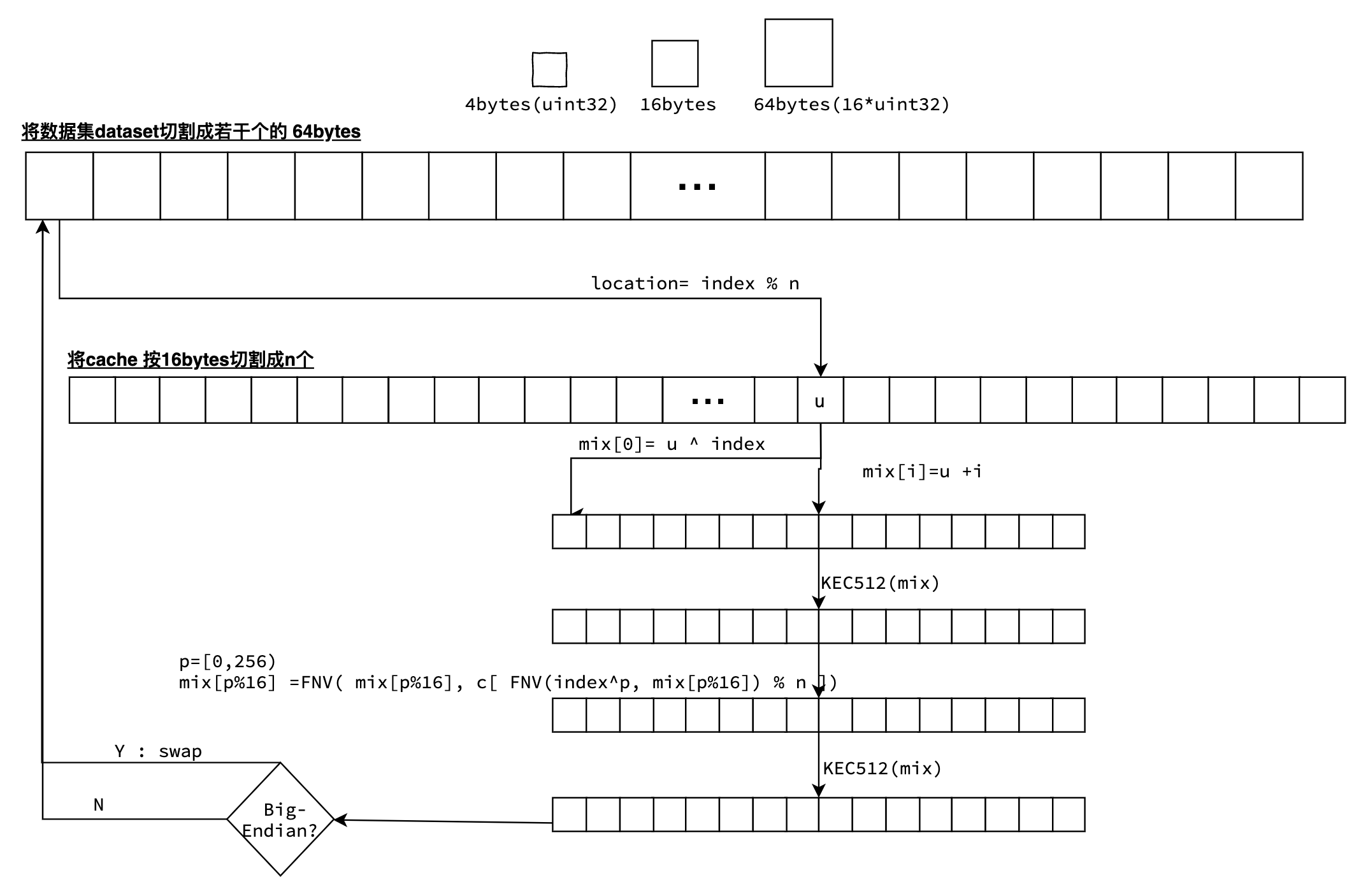
-
在生成index行的数据时,先从缓存中获取第 index % n 个单元的值u;
-
数据项mix长度64bytes,分割为4bytes的16个uint32。第一个uint32等于 u^index,其他第i个uint32等于u+i;
-
用数据项mix的Keccak512哈希值覆盖mix;
-
对mix进行FNV哈希。在FNV哈希时,是要从缓存中获取256个父项进行运算。
- 确定第p个父项位置: FNV(index^p , mix[p%16]) % n;
- 再将FNV( mix[p%16], cache[p] )的值填充到 mix[p%16]中; 其中,FNV(x,y)= x*0x01000193 ^ y ;这里的256次计算,相当于mix的16个uint32循环执行了16次。
-
再一次用数据项mix的Keccak512哈希值覆盖mix;
-
如果机器字节序是Big-Endian的,则还需要交换高低位;
-
最后将mix填充到数据集中,即 dataset[index]=mix;
注意,在FNV哈希计算中,初始大小1 GB数据集累积需要约42亿次(16777216 * 256) 次计算。即使并发计算,也需要一定的时间才能完成一次数据集生成。这也就是为什么在启动一个geth挖矿节点时,刚开始时会看到一段“Generating DAG in progress” 的日志,直到生成数据集完成后,才可以开始挖矿。
Ethash挖矿方程求解
准备好数据集dataset就可以用于工作量证明计算。依赖nonce、h、dataset可计算出的一个伪随机数N,工作量证明就是校验N是否符合难度要求。 工作量计算由挖矿方程Ethash定义。
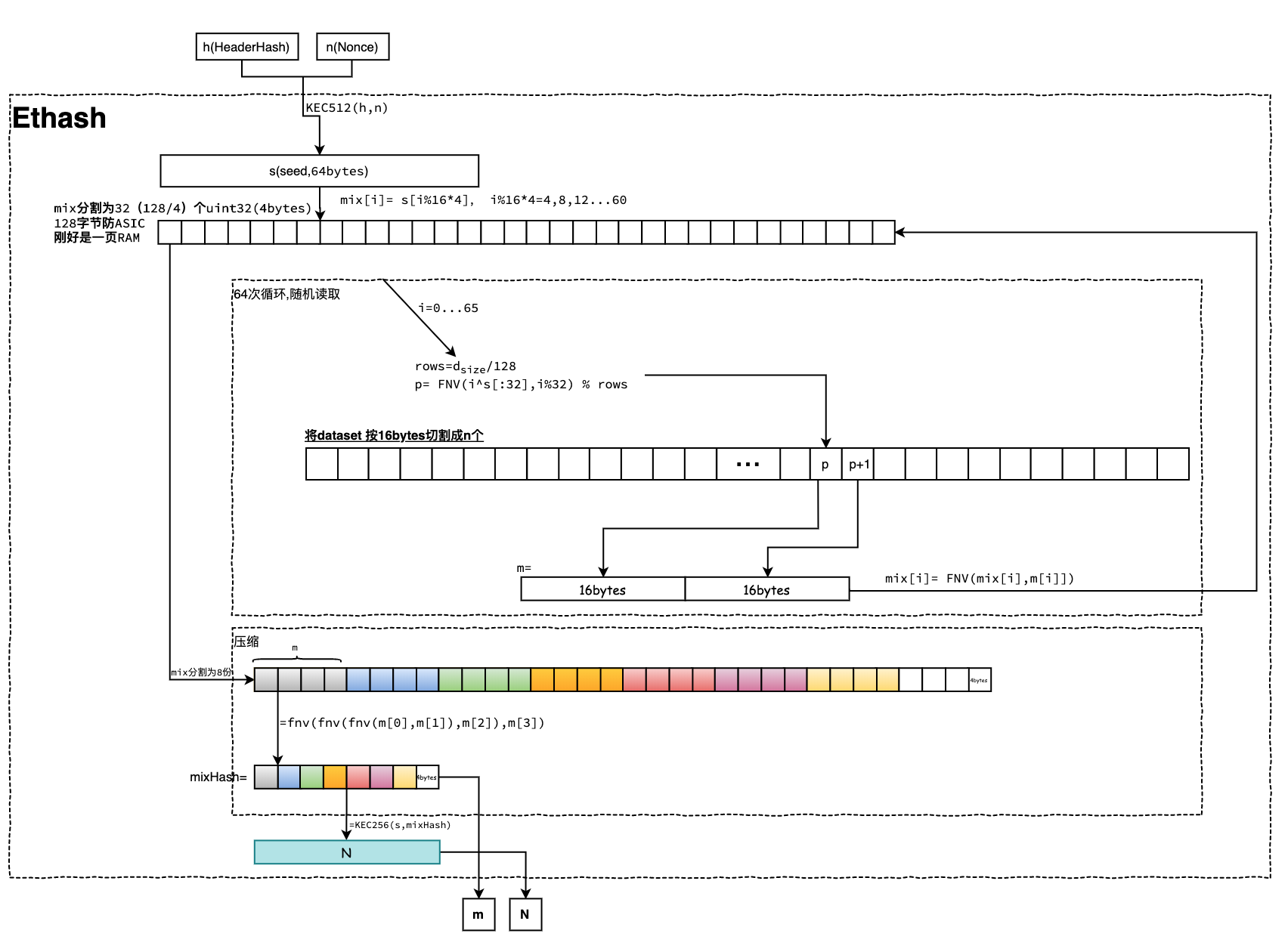
上图是Ethash的计算流程图。说明如下:
- 首先将传入的新区块头哈希值和随机数nonce拼接后进行KEC512哈希,得到64字节的种子seed;
- 然后初始化一个128字节长的mix,初始化时分割成32个4字节的单元;使用128字节的顺序访问,以便每次Ethash计算都始终从RAM提取整页,从而最小化页表缓存未命中情况。理论上,ASIC是可以避免的;
- mix数组的每个元素值来自于seed; mix[i]= s[i%16*4];是seed的第0、4、8...60位的值;
- 紧接着完成64次循环内存随机读写。 每次循环需要从 dataset 中取指定位置p(fnv(i^s[:32],i%32) % rows)和p+1上的两个16字节拼接成32字节的m;然后,使用fnv(mix[i],m[i])去覆盖mix[i]; 其中,i是循环索引、s[:32]是种子seed的前32字节、rows是表示数据集dataset可分成rows个128字节。
- 然后压缩mix。压缩是将mix以每16字节分别压缩得到8个压缩项。每16字节又是4小份的fnv叠加哈希值fnv(fnv(fnv(m[0],m[1]),m[2]),m[3]);
- 拼接这8个压缩项就得到mix的哈希值mixHash;
- 最后将seed和mixHash进行KEC256哈希得到伪随机数N;
- 最终,返回这两个参数:mixHash和N;
参考资料
- 太坊黄皮书
- go-ethereum
- 画图工具 Draw : https://www.draw.io
- 数学公式:LaTeX
- 扫了一眼 https://zhuanlan.zhihu.com/p/42694998
-----------------恭喜你,总算看完了!-------------------- 以上内容就是关于以太坊的工作量证明的说明。希望能帮助到你,记得点赞/分享让更多人知道!
- 以太坊 2026年协议级更新确定 3 大方向 239 浏览
- 寻找底线:为什么我们为 Layer 2 构建了紧急提款出口( Exit Hatch) 166 浏览
- 如何去中心化构建区块? 293 浏览
- Builder Codes & ERC-8021:修复链上归属问题 323 浏览
- 并行执行的谎言:为什么SOL和ZERO不是在与ETH竞争,而是在输给它的L2 363 浏览
- “夺旗”竞赛继续! 312 浏览
- EVM Gas 分析:新的执行跟踪数据 317 浏览
- 质押和链上信贷市场之间的微妙张力 425 浏览
- 以太坊应该停止担心扩展性,去做人们想要的东西 357 浏览
- Vitalik的L2重置:以太坊为何需要此航向修正 310 浏览
- 如何桥接到MegaETH(今天测试网,主网即将上线) 416 浏览
- Vitalik: 重新评估以太坊 Layer2 399 浏览

