深入解读 Uniswap V2 白皮书 【全网最详细】

引言

本文主要记录我个人对 uniswap v2 白皮书的解读，水平有限难免有错误之处，欢迎斧正。

旨在深入理解其中的数学原理，从而帮助进一步理解 代码的实现。

文章按照白皮书的目录进行解读，其中会加入一些个人的理解和思考。

1. Introduction

Uniswap v1是一个以太坊链上智能合约系统，实现了基于 𝑥⋅𝑦=𝑘 的AMM（自动做市）协议。每一个Uniswap v1交易对池子包含两种代币，在提供流动性的过程中保证两种代币余额的乘积无法减少。交易者为每次交易支付0.3%的手续费给流动性提供者。v1的合约不可升级。

Uniswap v2是基于同一个公式的新版实现，包含许多令人期待的新特性。其中最重要的一个特性是可以支持任意ERC20代币的交易对，而不是v1只支持ERC20与ETH的交易对。此外，v2提供了价格预言机功能，其原理是在每个区块开始时累计两种代币的相对价格。这将允许其他以太坊合约可以获取任意时间段内两种代币的时间加权平均价格；最后，v2还提供“闪电贷”功能，这将允许用户在链上自由借出并使用代币，只需在该交易的最后归还这些代币并支付一定手续费即可。

虽然v2的合约也是不可升级的，但是它支持在工厂合约中修改一个变量，以便允许Uniswap协议针对每笔交易收取0.05%的手续费（即0.3%的 1/6 ）。该手续费默认关闭，但是可以在未来被打开，在打开后流动性提供者将只能获取0.25%手续费，而非0.3%。

这里的数学原理将会在后面的 2.4 Protocol fee

在第三节，将介绍Uniswap v2同时修复了Uniswap v1的一些小问题，同时重构了合约实现，通过最小化（持有流动性资金的）core合约逻辑，降低了Uniswap被攻击的风险，并使得系统更加容易升级。

本文讨论了core合约和用来初始化交易对合约的工厂合约的结构。实际上，使用Uniswap v2需要通过router（路由）合约调用交易对合约，它将帮助计算在交易和提供流动性时需要向交易对合约转账的代币数量。

2. New feature

2.1 ERC-20 pairs

Uniswap v1 使用 ETH 作为桥梁货币。每对都包含 ETH 作为其资产之一。这使得路由更简单——ABC 和 XYZ 之间的每笔交易都经过 ETH/ABC 对和 ETH/XYZ 对——并减少了流动性的分散。

• V1 和 V2 工作原理的区别：

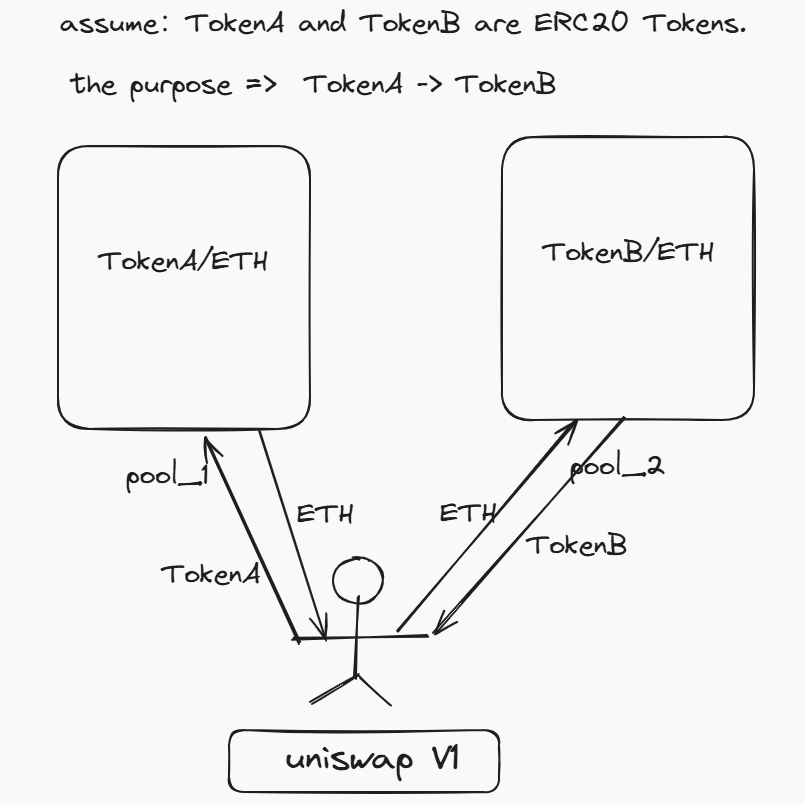
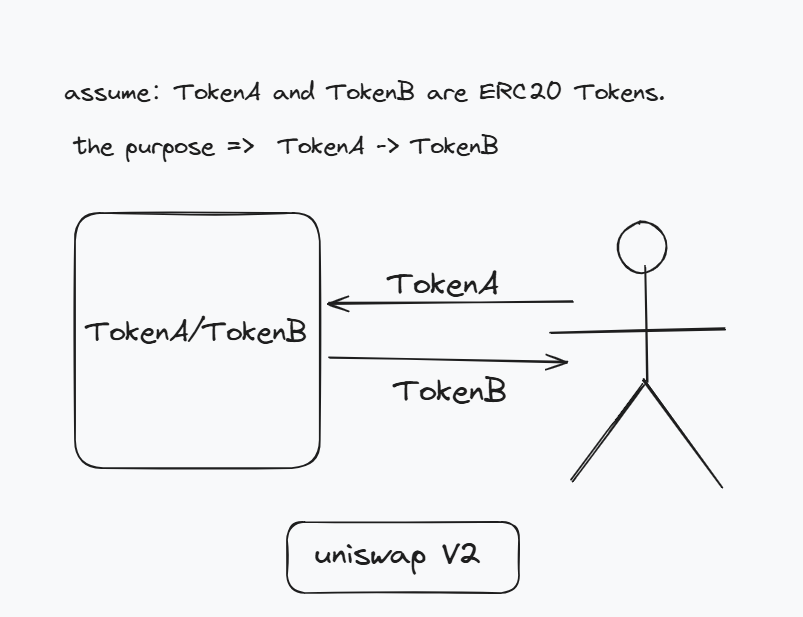
然而，这条规则给流动性提供者带来了巨大的成本。所有流动性提供者都接触 ETH，并根据其他资产相对于 ETH 的价格变化而遭受无常损失。当两种资产 ABC 和 XYZ 相互关联时——例如，如果它们都是美元稳定币——Uniswap 对 ABC/XYZ 上的流动性提供者通常会比 ABC/ETH 或 XYZ/ETH 对遭受更少的无常损失。

什么是无常损失？可以阅读 这篇文章。

可以举个实际案例分析：

LP亏损的资金便被称为无常损失。

这样看似乎，做LP反而会亏钱，但是实际上这部分的损失已经由用户的手续费冲淡了。（因为不断地收取用户的手续费，从而使得池子越来越深，LP可以从中获利。）

因为稳定币的价格比较稳定，不会像 ETH 有这么大的波动，所以相对来说遭受的无常损失较弱。

使用 ETH 作为强制性桥梁货币也会给交易者带来成本。交易者必须支付的费用是直接 ABC/XYZ 对的两倍，并且他们会遭受两次滑点。

Uniswap v2 允许流动性提供者为任意两个 ERC-20 创建配对合约。

v2不直接支持 ETH 的交易对，它需要 wrap 成遵循 ERC20 标准的 WETH Token。

任意 ERC-20 之间的配对激增可能会使找到交易特定配对的最佳路径变得更加困难，但可以在更高层处理路由（链下或通过链上路由器或聚合器）。

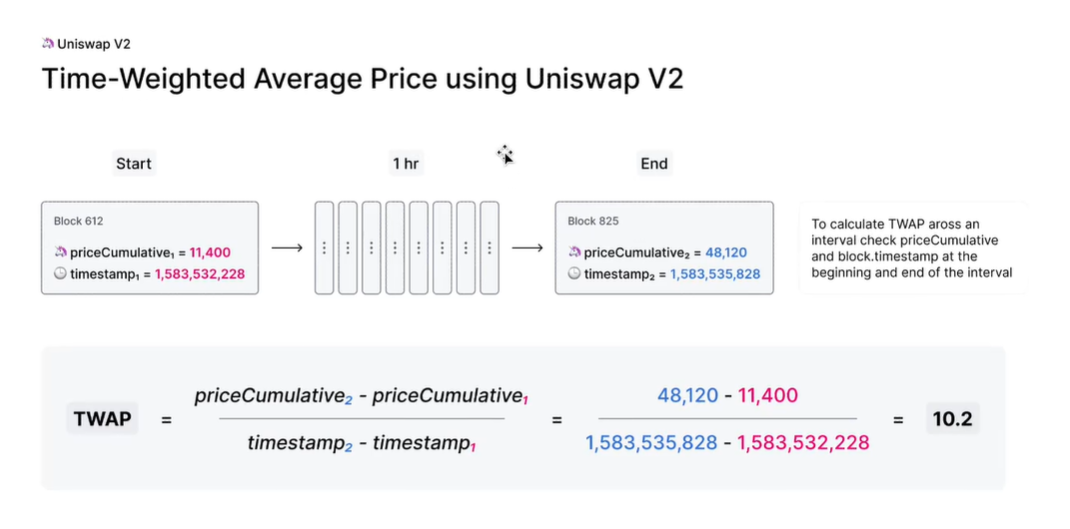
2.2 Price Oracle

价格预言机，理解起来有点挑战性，推荐一些参考资料

• link1
• link2
• link3
• 这篇文章讲的很不错：文章1
• 文章2

看图利于理解：

区块与区块之间不管间隔多久，都理解为价格不变，价格的变化只在区块中发生。

在时间点 $t$ 由Uniswap提供的边际价格（不包含手续费）可以通过代币a和代币b的数量相除得出：

$$ p_t = \frac {r ^ a_t} {r ^ b_t} $$

当Uniswap提供的价格不正确时，套利者可以在Uniswap交易套利（通过足够数量代币以支付手续费），因此Uniswap提供的代币价格将跟随市场价格。这意味着Uniswap提供的代币价格可以作为一种近似的价格预言机。

注：同一个代币在不同市场的价格差异提供了套利机会，驱使套利者维持Uniswap市场价格与其他市场（如中心化交易所或DEX）价格一致。

然而，Uniswap v1无法提供安全的链上预言机，因为它的价格很容易被操控。假设其他合约使用当前ETH-DAI价格作为衍生品交易的基准价格。攻击者可以从ETH-DAI交易对买入ETH来操控价格，并触发衍生品合约的清算，接着再将ETH卖回以使价格回归正常。上述操作可以通过一个原子交易完成，或者被矿工通过排序同一区块中的不同的交易来实现。

注：由于采样的价格是瞬时的，因此很容易通过买入卖出大额代币来操纵实时价格。

samczsun有一篇博客介绍了这种攻击。

Uniswap v2改进了预言机功能，通过在每个区块的第一笔交易前计算和记录价格来实现（等价于上一个区块的最后一笔交易之后）。操纵这个价格会比操纵区块中任意时间点的价格要困难。如果攻击者通过在区块的最后阶段提交一笔交易来操纵价格，其他套利者（发现价格差异后）可以在同一区块中提交另一笔交易来将价格恢复正常。矿工（或者支付了足够gas费用填充整个区块的攻击者）可以在区块的末尾操控价格，但是除非他们同时挖出了下一个区块，否则他们没有特殊的优势可以进行套利。

注：由于价格预言机仅在每个区块记录一次，因此除非同一个人控制了两个区块的所有交易，否则他们将没有足够的套利优势。但是这从另一方面说明，Uniswap v2的预言机仍然是不够健壮的。我们在v3可以看到这方面的改进。

Uniswap v2通过在每个区块第一笔交易前记录累计价格实现预言机。每个价格会以时间权重记录（基于当前区块与上一次更新价格的区块的时间差）。这意味着在任意时间点，该累计价格将是此合约历史上每秒的现货价格之和。

$$ at = \sum{i=1}^t p_i $$

为了估算在 $t_1$ 到 $t_2$ 时间段内的时间加权平均价格（TWAP），外部调用者可以分别记录 $t_1$ 和 $t_2$ 的累计价格，将 $t_2$ 价格减去 $t_1$ 价格，并除以 $t_2 - t_1$ 的时间差（需注意，合约本身不存储历史的累计价格，因此需要调用者在区间开始时调用合约，读取并保存当前的价格）。

$$ p_{t_1,t2} = \frac{\sum{i=t_1}^{t_2} p_i}{t_2 - t1} = \frac{\sum{i=1}^{t_2} pi - \sum{i=1}^{t_1} p_i}{t_2 - t1} = \frac {a{t2} - a{t_1}}{t_2 - t_1} $$

预言机的用户可以自行选择区间的开始和结束。选择一个更长的区间，意味着攻击者将花费更高的代价来操控该区间的时间加权平均价格，虽然这将导致该平均价格与实时价格相差较大。

注：公式(3)比较容易理解，这里就不展开。但是需注意，由于合约仅记录当前的累计价格，因此如果需要计算区间的平均价格，外部应用要自己记录并保存历史价格，合约本身不保存历史数据。

Uniswap v2的TWAP计算方式实际上使用的是（加权）算数平均数（Arithmetic Mean），这里我们需要了解几种平均数的概念和应用场景。

在数学上有一个毕达哥拉斯平均的概念，指的是三种经典平均数，分别是：算数平均数、几何平均数和调和平均数。

• 算数平均数 Arithematic Mean

$$ A(x_1,...,x_n) = \frac{1}{n}(x_1 + ... + x_n) $$

• 几何平均数 Geometric Mean

$$ G(x_1,...,x_n) = \sqrt[n]{x_1 ... x_n} $$

• 调和平均数 Harmonic Mean

$$ H(x_1,...,x_n) = \frac{n}{\frac{1}{x_1} + ... + \frac{1}{x_n}} $$

当 $x$ 为正数时，三者的关系：

$$ A(x_1,...,x_n) \geq G(x_1,...,x_n) \geq H(x_1,...,x_n) $$

其中，算术平均数是最常见的一种平均数，其优点是计算简单，缺点是容易受到极端数据的影响，导致均值误差；几何平均数相比算术平均数，更适用于在金融市场场景，因为金融市场价格本身是一种布朗运动；调和平均数更易受到极小值的影响，一般应用于计算平均速率等场景。

从应用场景上，Uniswap价格均值应该使用几何平均数更合适，均值的误差更小，但由于几何平均数在以太坊合约上实现难度较大，所以Uniswap v2版本采用算数平均数；但是Uniswap v3则使用几何平均数计算价格预言机。

在3.4节，Uniswap v2使用几何平均数计算初始流动性代币数量。

一个难题：我们应该计算以B代币计价的A代币价格，还是以A代币计价的B代币价格？虽然在现货价格上，以B代币计价的A代币价格（B/A）与以A代币计价的B代币价格（A/B）总是互为倒数，但在计算某个时间区间的算数平均数时，二者却不是互为倒数关系。比如，假设在区块1的价格为100 USD/ETH（B为USD，A为ETH），区块2的价格为300 USD/ETH，则其平均价格为200 USD/ETH，但ETH/USD的平均价格却是1/150 ETH/USD。因为合约无法知道交易对中哪一个代币将被用户用作计价单位，因此Uniswap v2同时记录了两个代币的价格。

注：两种代币计价的均值计算如下：

• 以 USD 计价

$$ A(x_1, x_2) = \frac{100 + 300}{2} = 200 \text{ USD/ETH} $$

• 以 ETH 计价

$$ A(\frac{1}{x_1}, \frac{1}{x_2}) = \frac{\frac{1}{100} + \frac{1}{300}}{2} = \frac{1}{150} \text{ ETH/USD} $$

另一个难题是用户可以不通过交易而直接向交易对合约发送代币（这将改变代币余额并影响价格），此时将无法触发预言机价格更新。

注：因为预言机价格需要在区块的第一笔交易之前更新，因此如果不交易，将绕开预言机更新。

如果合约只是简单地检查它的余额，并使用当前余额计算价格来更新预言机，那么攻击者可以在区块的第一笔交易之前，立即向合约发送代币来操控预言机价格。如果上一笔交易是在 $x$ 秒之前的某个区块，合约将错误的使用（被操纵后的）新价格乘以 $x$ 来累计，即使并没有人使用该价格交易过。

注：假设在上一个区块最后一笔交易后，交易对合约中两个代币A、B的余额分别为100、200，以A计价的B价格为 $\frac{200}{100}=2$ ，在 $x$ 秒后，下一个区块第一笔交易发生之前，应该累计的价格是 $2x$ ，但是如果在第一笔交易发生之前，攻击者向合约发送了100个B，此时价格为 $\frac{200}{200}=1$ ，合约将错误地以 $1x$ 累计。

为了防止这个问题，core合约在每次交互后缓存了两种代币余额，并且使用缓存余额（而非实时余额）更新预言机价格。除了防止预言机价格被操控外，这个改动也带来了合约架构的重新设计，我们将在3.2节进行说明。

2.2.1 Precision 精度

因为Solidity原生不支持非整数数据类型，Uniswap v2使用了简单的二进制定点制进行编码和操作价格。确切地说，任意时间的价格都被保存为UQ112.112格式的数据，它表示在小数点的左右两边都有112位比特表示精度，无符号（注：非负数）。这个格式能表示的范围为 $[0, 2^{112}-1]$ ，精度为 $\frac{1}{2^{112}}$ 。

注：UQ112.112的理论最大值为： $2^{112}-\frac{1}{2^{112}}$ ，但由于Uniswap v2使用两个uint112相除得到UQ112.112，因此其最大值为 $2^{112}-1$ 。

选择UQ112.112格式是出于（Solidty合约）编程实践的考虑，因为这些格式的数字能够使用一个uint224类型（占用224位比特，28个字节）的变量表示，在一个256位（比特）的存储槽（注：EVM中一个Storage Slot是256位）中正好剩余32位可用。而对于缓存的代币余额变量，每一个代币余额可以使用一个uint112类型（112比特位，14个字节）的变量，（在声明时）也正好在256位的存储槽中剩余32位可用。这些剩余空间可用于上述的累计运算使用。具体来说，代币余额与最近一个有交易区块的时间戳一起保存，该时间戳针对 $2^{32}$ 取模，以确保可以使用32位表示。此外，虽然在任意时间点的价格（使用UQ112.112格式的数字）一定符合224位，但是一段时间的累计价格却不是这样。在存储槽末尾的多余32位空间将用于存储由于重复累计价格导致的溢出数据。这样的设计意味着价格预言机仅仅在每个区块的第一笔交易增加了3个SSTORE操作（当前消耗15,000 gas）。

注：这里我们可以看到Uniswap在设计上是非常小心的，价格预言机虽然是一个很有用的功能，但是却不能因为过度设计而给用户增加成本，因此如何在确保对用户影响最小的同时把功能实现，就成为设计的核心所在。为了避免每次交易都更新预言机给用户带来额外交易成本，Uniswap v2才设计成只在每个区块的第一笔交易之前更新。

每个代币余额使用uint112表示，时间戳使用32位表示，总共112+112+32=256位，正好占用一个storage slot。更少的storage slot意味着交互时需要花费的gas更小，有利于减少用户操作成本。累计价格则采用256位表示。

这个设计最主要的缺点是32位无法确保时间戳永不溢出。事实上，Unix时间戳溢出32位（可表示的最大值）将发生在02/07/2106。为了确保系统能够在该时间后正常工作，同时在每一轮32位溢出后（ $2^{32}-1$ 秒）也能正常工作，预言机需要至少在每一轮（大约136年）被调用查询一次。因为累计计算的核心方法是溢出安全的，这意味着即使交易跨越了时间戳溢出的时间点，它也是可以被正常累计的，只要预言机使用了正确的溢出算法来检查时间间隔。

注：这里我们主要关注在时间戳溢出边界，使用公式（3）是否能够正确算出预言机价格的平均数。假设在2106年2月7日附近， $t_1,t_2,t_3$ 分别表示三个连续的区块时间，其中 $t_1$ 未发生时间戳溢出（差1秒），而 $t_2$ , $t_3$ 则发生溢出，可以算出即使在溢出后， $t_2 - t1$ 仍然可以计算出正确的时间差（3秒）；同理可以计算即使当累计价格 $a{t3}$ 发生溢出后，只要调用者保存了 $a{t1}$ 的值，即可计算出二者正确的差值。 $p{t_1,t_3}$ 为 $t_1$ 到 $t_3$ 时间区间的平均价格，按照公式（3）可推出如下计算：

$uint32.max = 2^{32} - 1 = 4,294,967,295$

$t_1 = 4,294,967,294$

$t_2 = 4,294,967,297 \% 4,294,967,296 = 1$

$t_3 = 4,294,967,301 \% 4,294,967,296 = 5$

$\Delta{t_1,t_2} = 1 - 4,294,967,294 = -4,294,967,293 = 3$

$\Delta{t_2,t_3} = 5 - 1 = 4$

$\Delta{t_1,t_3} = 5 - 4,294,967,294 = -4,294,967,289 = 7$

$p_{t_1} = 100$

$p_{t_2} = 110$

$a_{t_1} = 1000$

$a_{t2} = a{t1} + p{t_1} \Delta{t_1,t_2} = 1000 + 100 3 = 1300$

$a_{t3} = a{t2} + p{t_2} \Delta{t_2,t_3} = 1300 + 110 4 = 1740$

$$ p_{t_1,t3} = \frac {a{t3} - a{t_1}}{t_3 - t1} = \frac {\Delta{a{t1},a{t_3}}} {\Delta{t_1,t_3}} = \frac {740}{7} = 105.71 $$

2.3 Flash Swaps

在Uniswap v1，用户如果想使用XYZ购买ABC，则需要先将XYZ发送到合约才能收到ABC。这将给那些希望使用ABC购买XYZ的用户带来不便。比如，当Uniswap与其他合约出现套利机会时，用户可能希望使用ABC在别的合约购买XYZ；或者用户希望通过卖出抵押物来释放他们在Maker或Compound的头寸，以此偿还Uniswap的借款。

Uniswap v2增加了一个新特性，允许用户在支付费用前先收到并使用代币，只要他们在同一个交易中完成支付。swap方法会在转出代币和检查k值两个步骤之间，调用一个可选的用户指定的回调合约。一旦回调完成，Uniswap合约会检查当前代币余额，并且确认其满足k值条件（在扣除手续费后）。如果当前合约没有足够的余额，整个交易将被回滚。

用户可以只归还原始代币，而不需要执行交易操作。这个功能将使得任何人可以闪电借出Uniswap池子中的任意数量的代币（闪电贷手续费与交易手续费一致，都是0.30%）。

这是 uniswap 提供的闪电贷功能，虽然很实用，但是也埋下了不少隐患。（重入攻击）

2.4 Protocol fee

Uniswap v2包含一个0.05%的协议手续费开关。如果打开，该手续费将被发送到合约中的feeTo地址。

默认情况下没有设置feeTo地址，因此不收取协议手续费。预定义的feeToSetter地址可以调用Uniswap v2工厂合约中的setFeeTo方法来修改feeTo地址。feeToSetter也可以调用setFeeToSetter修改合约中feeToSetter地址。

如果feeTo地址被设置了，协议将开始收取5个基点（0.05%）的手续费，也就是流动性提供者收取的30个基点（0.30%）手续费中的1/6将分配给协议。这意味着交易者将继续为每一笔交易支付0.30%的交易手续费，83.3%（5/6）的手续费（整笔交易的0.25%）将分配给流动性提供者，剩余的16.6%（手续费的1/6，整笔交易的0.05%）将分配给feeTo地址。

如果在每笔交易时收取0.05%的手续费，将带来额外的gas消耗。为了避免这个问题，累计的手续费只在提供或销毁流动性时收取。合约计算累计手续费，并且在流动性代币铸造或销毁的时候，为手续费受益者（feeTo地址）铸造新的流动性代币。

在理解白皮书的公式之前，需要提前知道收取手续费的方式。

参考资料：link。

1. 通过增发share的方式把手续费给项目方（即lp持有的lp的价值不变，手续费全给项目方[feeTo]）

2. 不增发share，让原来的share更值钱（由于手续费的积累，池子越来越深，share也更值钱了）。

3. 项目方要分走一定比例 ${\phi}$ 的手续费，这也是 v2 采用的模式。

总累计手续费可以通过计算从上次收取手续费后，以 $\sqrt{k}$（也就是 $\sqrt{x \cdot y}$ ）计价的增长量。可计算从 $t_1$ 到 $t_2$ 的累计手续费，与 $t_2$ 时刻的流动性的百分比如下：

$$ f_{1,2} = 1 - \frac{\sqrt{k_1}}{\sqrt{k_2}} $$

如果协议手续费在 $t_1$ 之前被激活，那么在 $t_1,t2$ 时段，feeTo地址应该收取 $\frac{1}{6}$ 的手续费作为协议手续费。因此，我们需要为feeTo地址铸造新的流动性代币以代表该时段手续费，这里等于 $\frac{1}{6} \cdot f{1,2}$。

假设协议手续费对应的流动性代币数量为 $s_m$ ， $s_1$ 为 $t_1$ 时刻的流动性代币数量，则有以下等式：

$$ \frac{s_m}{s_m + s1} = \phi \cdot f{1,2} $$

替换 $f_{1,2}$ ，经过计算可以得出 $s_m$ 为：

$$ s_m = \frac{\sqrt{k_2} - \sqrt{k_1}}{(\frac{1}{\phi} - 1) \cdot \sqrt{k_2} + \sqrt{k_1}} \cdot s_1 $$

替换其中的比例部分，可得：

$$ s_m = \frac{\sqrt{k_2} - \sqrt{k_1}}{5 \cdot \sqrt{k_2} + \sqrt{k_1}} \cdot s_1 $$

假设初始流动性提供者存入100 DAI和1 ETH，获得10个流动性代币。一段时间后（假设没有其他流动性提供者），当feeTo希望取出协议手续费时，两种代币余额分别为96 DAI和1.5 ETH。分别代入公式可得：

$$ s_m = \frac{\sqrt{1.5 \cdot 96} - \sqrt{1 \cdot 100}}{5 \cdot \sqrt{1.5 \cdot 96} + \sqrt{1 \cdot 100}} \cdot 10 \approx 0.0286 $$

2.5 Meta transactions for pool shares

Uniswap v2的池子份额（即流动性代币）天然支持元交易。这意味着用户可以通过签名授权第三方转移其持有的流动性代币，而无需通过他们自己发起链上交易。任何人都可以通过调用permit方法来代替该用户提交签名，支付gas费用，并且可以在同一交易中执行其他操作。

permit 方法是在 EIP-2612 中提出。

现在这种方法在 ERC20Permit.sol中，已经被实现了，link。

3. Other changes

3.1 Solidity

Uniswap v1使用Vyper语言实现，这是一个类Python的智能合约语言。Uniswap v2使用更流行的Solidity语言实现，因为v2依赖一些（在开发时）Vyper语言还不具有的能力，比如解析非标准ERC-20代币的返回值，通过内联的assembly语法访问一些新操作码，如chainid。

3.2 Contract re-architecture

Uniswap v2的一个设计重点在于最小化core交易对合约的对外接口范围和复杂度（core合约存放流动性提供者的代币资产）。在core合约上发现的任何bug都可能是灾难性的，因为这可能会导致数百万美元的流动性资产被盗走或冻结。

在评估core合约的安全性时，最重要的问题是它是否能保护流动性提供者的资产不被盗走或冻结。任何增强或保护交易者的功能特性，而不是允许池子里资产交换这种最基本的功能，都应该被抽取放到router（路由）合约。

事实上，甚至部分swap功能的代码也可以被提到router合约中。如前所述，Uniswap v2保存每种代币最后的余额记录（为了防止攻击者操纵预言机机制）。新的架构在此基础上针对Uniswap v1做了进一步简化。

在Uniswap v2，卖方在执行swap方法前，会发送代币到core合约。合约将通过比较缓存余额和当前余额来判断收到多少代币。这意味着core合约无法知道交易者是通过什么方式发送代币。事实上，他可以通过离线签名的元交易方式，或者其他未来授权ERC-20代币转移的机制，而不只是transferFrom方法。

3.2.1 Adjustment for fee

Uniswap v1的交易手续费是通过减少存入合约的代币数量来实现，在比较k常值函数之前，需要先减去0.3%的交易手续费。合约隐式约束如下：

$$ (x1 - 0.003 \cdot x{in}) \cdot y_1 \geq x_0 \cdot y_0 $$

通过闪电贷功能，Uniswap v2引入了一种可能性，即 $x_in$ 和 $y_in$ 可能同时不为0（当一个用户希望通过归还借出的代币，而不是做交易时）。为了处理这种情况下的手续费问题，合约强制要求如下约束：

$$ (x1 - 0.003 \cdot x{in}) \cdot (y1 - 0.003 \cdot y{in}) \geq x_0 \cdot y_0 $$

注：Uniswap的swap方法可以同时支持闪电贷和交易功能，当通过闪电贷同时借出x和y两种代币时，需要分别对x和y收取0.3%的手续费，因此需要先扣除手续费，再保证余额满足k值约束。

为了简化链上计算，我们可以为公式两边同时乘以1,000,000，得出：

$$ (1000 \cdot x1 - 3 \cdot x{in}) \cdot (1000 \cdot y1 - 3 \cdot y{in}) \geq 1000000 \cdot x_0 \cdot y_0 $$

3.2.2 sync() and skim()

为了防止某些可以修改交易对合约余额的定制代币，同时也为了更优雅地解决那些总量超过 $2^{112}$ 的代币，Uniswap v2提供了两个方法：sync()和skim()。

当某种代币异步通缩时，sync()可以作为一种恢复手段。在这种场景下，交易将获得次优的兑换率，如果没有流动性提供者愿意纠正这种状态，交易对将难以继续工作。sync()方法可以将合约中缓存的代币余额设置为当前实际余额，以帮助系统从这种状态中恢复。

当发送大量代币导致交易对的代币余额溢出（超过uint112最大值）时，交易将失败，skim()可以作为这种情况的恢复手段。skim()允许任意用户取出多余的代币（代币实际余额与 $2^{112}-1$ 的差值）。

3.3 Handling non-standard and unusual tokens

ERC-20标准要求transfer()和transferFrom()返回一个布尔值表示该请求是否成功。然而某些代币在实现这两个（或其中一个）方法时并没有返回值，比如USDT和BNB。Uniswap v1在解析无返回值的方法时，将其当作失败处理，因此将回滚交易，从而导致交易失败。

扩展阅读： EIP-20: ERC-20代币标准 USDT合约地址 BNB合约地址

Uniswap v2针对非标准ERC-20代币的实现，则使用不一样的处理方法。当transfer()方法没有返回值时，Uniswap v2认为它表示执行成功，而非失败。这个改动不会影响任何实现标准ERC-20的代币（因为他们的transfer()方法有返回值）。

同样，Uniswap v1假设transfer()和transferFrom()不能触发重入交易对合约的方法。这种假设会和某些ERC-20代币冲突，包括那些支持ERC-777标准hooks的代币。为了完全支持这些代币，Uniswap v2引入了"lock"机制用来解决所有公开修改状态方法的重入问题。这也可以防止在闪电贷中用户自定义回调的重入问题。

注：lock实际上是一个Solidity modifer，通过一个unlock变量控制同步锁。

3.4 Initialization of liquidity token supply

当一个新的流动性提供者将代币存入一个已存在的Uniswap交易对，新铸造的流动性代币数量可根据当前代币数量计算：

$$ s{minted} = \frac{x{deposited}}{x{starting}} * s{starting} $$

这里 ${s_{minted}}$ 其实本身也是一种ERC20 Token，持有的流动性 Token的数量即表示占有该交易池的份额（一般称之为share）。

当往现有的交易对，且不是第一个流动性提供者，那么存入的代币价值和总价值的比例，与其得到的 LP Token数量和 LP Token 的总数量（可以通过totalSupply()获取）的比例相等。即

$$ \frac {s{minted}} {s{starting}} = \frac {x{deposited}} {x{starting}} $$

但是在实际的代码实现中，只需要比较 $\frac {x_{deposited}}{x_0}$ ，其中x指的交易对中的某个代币，比如ETH/DAI中的ETH， ${x_0}$ 指未添加流动性前x的数量。白皮书这里没有说x是什么，所以我尝试着理解为 x*y的乘积开根号算出来的结果也没错。推导过程如下：

举个实际案例：往 ETH/DAI 交易池中添加流动性即做lp。

$$ state_0 ==> ETH = 10 : DAI = 100, add => ETH=2,DAI=20 $$

如果采用上述文字部分的推导，则计算过程如下：

$$ s_{minted} = \frac {\Delta {ETH}} {{ETH}_0} s_1 = \frac {2} {10} s_1 = 0.2 *s_1 $$

如果采用的是图中的推导，则计算过程如下：

$$ \sqrt {k_1} = \sqrt {x_0 y_0} = \sqrt {10 100},\sqrt {k_2} = \sqrt {x_1 y_1} = \sqrt {12 120} $$

$$ s_{minted} = \frac {{\sqrt k_2} - {\sqrt k_1}} {\sqrt k_1} s_1 = \frac {{\sqrt {12 120}} - {\sqrt {10 100}}} {\sqrt{10 100}} s_1 = 0.2 s_1 $$

由此可见，结果是一致的，感觉两种方式都可以，但是还是推荐文字版推导，因为白皮书是这么写的。

但如果他们是第一个流动性提供者呢？在这种情况下， $x_{starting}$ 是0，因此上述公式无法适用。

Uniswap v1将首次流动性代币数量等同于存入的ETH数量（以wei为单位）。这有一定的合理性，因为如果首次流动性是以正确的价格存入的，那么1个流动性份额（如ETH是一种有18位小数的代币）将代表大约2ETH的价值。

这里是什么意思，为什么是2 ETH？

答：因为Uniswap v1 / v2提供流动性时需要注入两边等值的代币，如果份额等同于ETH数量，则1份额表示需要存入1ETH，而在价格正确时，另一个代币的价值也同样是1ETH，因此1个流动性份额的流动性总价值是2ETH。

然而，这意味着流动性份额的价值需要依赖首次注入流动性时的价格比例，而这个价格是可以被认为控制的，我们无法保证首次注入流动性时的两种代币的比例能够正确反映真实价格。此外，由于Uniswap v2支持任意代币的交易对，因此将有更多的交易对不包含ETH。

与v1不同，Uniswap v2规定首次铸造流动性代币的数量等于存入的两种代币数量的几何平均数：

$$ s{minted} = \sqrt {x{deposited} * {y_{deposited}}} $$

该公式确保在任意时刻，流动性份额的价值与其存入代币的价格比例无关。比如，假设当前1 ABC的价格是100 XYZ，如果首次存入2 ABC和200 XYZ（对应的比例为1:100），则流动性提供者将收到 $\sqrt {2 * 200} = 20$ share。这些share代币价值2 ABC和200 XYZ，以及对应的累计手续费。

如果首次存入2 ABC和800 XYZ（对应比例1:400），则流动性提供者将收到 $\sqrt {2 * 800} = 40$ share。

以上公式确保1个流动性份额（代币）的价值将不少于池子中两种代币余额的几何平均数。然后，1个流动性代币的价值将可能随着时间持续增长，比如通过累计交易手续费，或者通过其他人“捐赠”代币到池子里。

这里的 捐赠其实指那些往池子中转入代币，或者在执行 swap()函数的时候多偿还手续费等等。

理论上可能存在这种情况，最小的流动性代币单位（ 1e-18 ，即1 wei）的价值太高，以至于无法让其他（小）流动性提供者加入。

为了解决这个问题，Uniswap v2销毁首次铸造 1e−15（最小代币单位的1000倍）share。这个损耗对于大部分交易对而言都是微不足道的。但是这将极大提高首次铸币攻击的代价。为了将每个share价格提高到100美元，攻击者需要捐赠10万美元的代币到池子中，这些代币将被作为流动性而永久锁定。

这里很有意思，必须要仔细讲讲如何提高攻击者代价。

        if (_totalSupply == 0) {
            liquidity = Math.sqrt(amount0.mul(amount1)).sub(MINIMUM_LIQUIDITY);
           _mint(address(0), MINIMUM_LIQUIDITY); // permanently lock the first MINIMUM_LIQUIDITY tokens
        }

这里的 MINIMUM_LIQUIDITY = 10 ^ 3 wei，永久封锁这 MINIMUM_LIQUIDITY便提高了攻击者攻击的代价。

攻击原理是使用极小的 share 来操控着大量资金。（攻击逻辑可以通过编写攻击合约实现）

• 当 hacker 首次添加流动性的时候，存入了最小单位的流动性 1 wei即 1e-18，比如 1 wei A Token 和 1 wei B Token，此时铸造的 share 为 $\sqrt { 1 * 1}$ ；
• 此外hacker在同一笔交易中通过代币的转账函数往池子中转入大量的A Token 和 B Token（这种转账方式不会 mint share），假设 1e8 个 A Token，1e8 个 B Token；
• 让在同一笔交易中，在转账逻辑之后调用池子中的sync()函数，更新池中两种代币的reserve，此时 1 wei 的 share 对应的价值为 (1e8 + 1e-18) 个 A Token 和 (1e8 + 1e-18) 个 B Token。

那么此时如果其他的用户想要添加流动性的话会发生什么情况呢？

$$ s{minted} = \frac{x{deposited}}{x{starting}} * s{starting} $$

从这个公式中不难得到：

$$ s{minted} = \frac{x{deposited}} {{10 ^ {8} + {10 ^ {-18}}}} * 1wei $$

在solidity语法中，对于小数的值都是采取向下取整的操作，所以用户投入的资金价值至少要大于等于(1e8 + 1e-18) * 2 ，否则share的值都是0，这极大的提高了做 lp 的门槛。

但是，直接锁掉 MINIMUM_LIQUIDITY数量的 share，而且hacker还是使用如上的攻击原理，如果hacker仍想给自己 铸造 1 wei 的 share，那 ta 必须要 添加 1001个 A Token 和 1001个B Token，因为 ${\sqrt {1001 1001}} - 1000 = 1$ 。接着通过 “捐赠”的方式想将 share的价值提高到 100$，那么ta则需要”捐赠“ 价值 1001 100$的 Token。

3.5 Wrapping ETH - WETH

使用以太坊原生代币ETH进行交易的接口，与使用ERC-20代币的接口是不同的。因此，许多以太坊协议并不支持ETH，而使用一种符合ERC-20标准的代币封装ETH，即WETH。

Uniswap v1是一个例外。因为每一个Uniswap v1交易对都使用ETH作为其中一种交易代币，因此直接支持ETH交易是合理的，并且能够更省gas。

由于Uniswap v2支持任意ERC-20交易对，因此没有必要支持原生ETH交易。增加这种支持将使core合约代码量翻倍，并且将使流动性分裂为ETH和WETH交易对。原生ETH需要先封装为WETH才能在Uniswap v2交易。

3.6 Deterministic pair address

与Uniswap v1一样，所有Uniswap v2交易对合约都由一个统一的工厂合约初始化生成。在Uniswap v1，这些合约使用CREATE操作码创建，这意味着这些合约的地址依赖于合约生成的顺序。Uniswap v2使用以太坊新的CREATE2操作码生成具有确定地址的交易对合约。这意味着交易对合约的地址是可以通过链下计算的，而无需查询链上状态。

3.7 Maximum token balance

为了更有效地实现预言机功能，Uniswap v2只支持缓存代币余额的最大值为 $2^{112}-1$ 。该数字已经大到可以支持代币总量超过千万亿的18位小数代币。

如果任意一种代币余额超过最大值，swap方法的调用将会失败（由于_update()方法的检查导致）。为了从这种状况中恢复，任何人都可以调用skim()方法来从池子中移除多余的代币。

思考

swap导致价格波动的原因

UNISWAP 围绕着 x * y = k 这个恒定乘积执行代币的swap操作。

$$ x * y = k
$$

如果 userA 使用 ${\Delta x}$ 数量 的 TokenA 去兑换 TokenB，有

$$ y'_1 = \frac {k} {x_0 + \Delta x} $$

如果 userB 使用 ${\Delta x}$ 数量 的 TokenA 去兑换 TokenB，有

$$ y'_2 = \frac {k} {x_0 + \Delta x + \Delta x} $$

不难看出 ${y'_2}$ 的值肯定是要比 ${y'_1}$ 的值要小的，从而反映出 TokenB的价格升高了。

这是因为 TokenA 的数量变多了，即使 userB 和 userA 的 TokenA 数量相同，那么后来者的 TokenA 将会对池子中TokenA的数量影响将会被削弱，即池子TokenA的数量将不会受到同样大幅度的影响。

举个例子，假如ETH/DAI池子中的资金为：ETH(100):DAI(10000)，K = 100 * 10000 = 1e6

$$ state_0: K = 1e6, ETH=100, DAI=10000 $$

假设userA使用10个ETH兑换DAI，有

$$ y'_1 = \frac {k} {x_0 + \Delta x} = \frac {1e6} {100 + 10} \approx 9090.9 $$

$$ \Delta y_1 = y_0 - y'_1 = 10000 - 9090.9 = 909.1 DAI $$

$$ state_1: K = 1e6, ETH=110, DAI=9090.9 $$

假设userB也使用10个ETH兑换DAI，有

$$ y'_2 = \frac {k} {x_1 + \Delta x} = \frac {1e6} {110 + 10} \approx 8333.3 $$

$$ \Delta y_2 = y_0 - y'_2 = 9090.9 - 8333.3 = 757.6 DAI $$

$$ state_2: K = 1e6, ETH=120, DAI=8333.3 $$

userB也是使用10 ETH兑换 DAI，换出来的DAI要少于userA兑换的DAI，说明TokenB的价格变高了。

TokenA 和 TokenB 在池中的数量变换关系为：

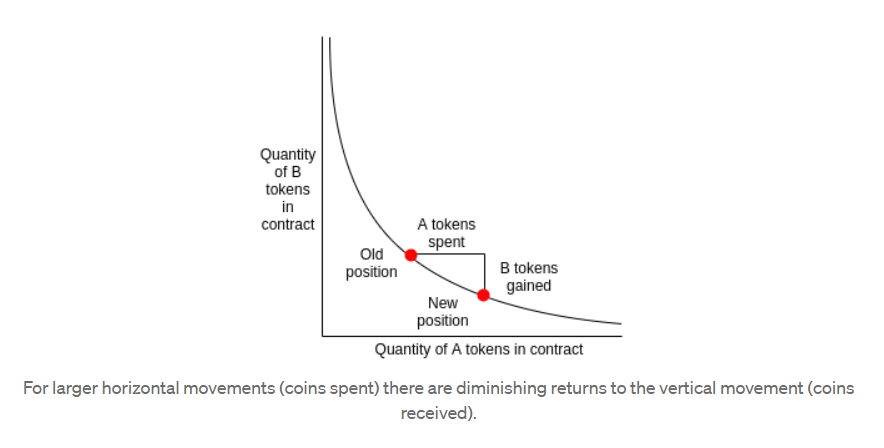
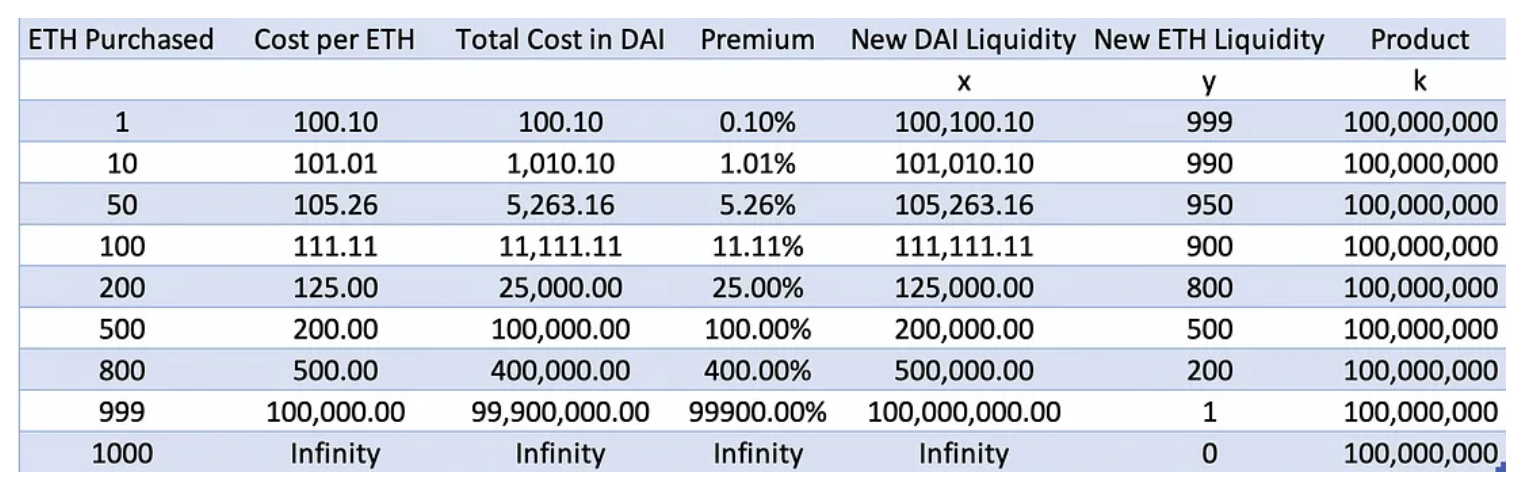
代码测试

链接：https://github.com/LBiyou/DeFi-Learning/tree/main/uniswap/v2/contracts

参考资料

• link1

最后码字不易，点个赞支持一下🤪~