加密工具101 - 哈希函数与默克尔树

13 min read 2023年9月25日

本文内容是什么？

区块链使人们能够在不需要中介的情况下达成共识。区块链并不依赖于信任，而是依赖于加密证明。加密原语用于提供这些证明。但它们是什么？

在本文中，我们将介绍两个对区块链的加密证明至关重要的加密原语：哈希函数和默克尔树。我们将探讨哈希函数的核心机制，了解它们对区块链的重要性，并学习哈希指针。接着，我们将考察传统和并发默克尔树，并概述它们对Solana的重要性。

什么是加密原语？

加密原语是构建加密协议和系统的基础操作或算法。从加密原语到加密协议，就像原子和分子一样 —— 它们是更复杂解决方案的构建块。随机数生成器、承诺方案和公钥加密都是加密原语的例子。

单独的加密原语相当有限。组合后的加密原语提供基本的安全功能，例如身份认证、保密性和完整性。组合加密原语是一个非常微妙的过程，需要充分的规划以及对每个原语相互作用的深刻理解。在这个过程中，你必须关注安全考虑，以实现所希望的安全目标。组合加密原语的方法可以大致分为：

• 顺序组合：一个接一个地应用原语（例如，哈希链接）
• 并行组合：同时并独立地使用原语（例如，同时对数据进行加密和哈希处理）
• 分层组合：在另一个加密原语内部使用原语（例如，默克尔树）

理解什么是加密原语，它们的工作原理，以及组合它们时涉及的微妙问题，帮助你理解并设计安全有效的系统。哈希函数是最常用且常被组合的加密原语之一。

什么是哈希函数？

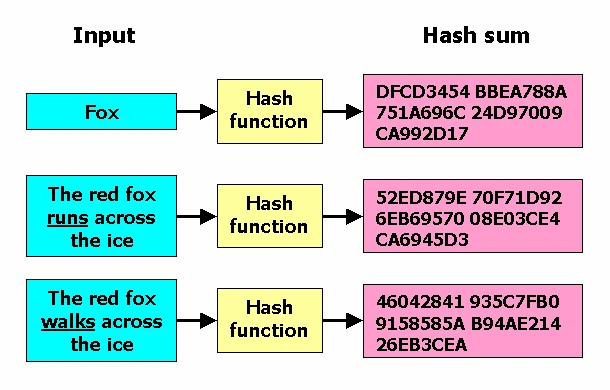
哈希函数是一种加密函数，它接受任意大小的数据，并返回一个固定大小的值。这个函数返回的值称为摘要，或称为 hash。流行的哈希算法包括：SHA-1、SHA-2、SHA-3、MD5 和 Argon2。哈希函数在区块链中无处不在，因此理解它们是什么以及它们如何工作是至关重要的。

一个简单的类比

想象一下烘焙一块华丽的巧克力蛋糕。蛋糕有多个层次，每一层都有自己的配料。在烘焙的时候，你的朋友给你发短信问你在做什么。给朋友详细解释制作蛋糕的过程和使用的所有配料会非常繁琐。相反，你决定给朋友发送一张巧克力蛋糕的照片。

在这里，蛋糕的照片就相当于一个哈希——它是对更复杂事物的简单、紧凑的表示。你的朋友不会知道你做蛋糕用到了每一种配料，但他们会对你刚刚烤好的东西有一个大概的了解。假设你的巧克力蛋糕上面放了覆盆子。如果你把它们拿掉或者换成草莓，那蛋糕的照片就会和最终产品完全不同。同样，对哈希的数据进行的任何更改都将产生一个新的哈希值。

良好加密哈希函数的特性

诚然，之前给出的哈希函数的定义是具有误导性的。哈希函数可能会返回可变大小的哈希。它还可能对两个不同的输入返回相同的哈希。并且，要想逆向工程找到原始输入，可能非常简单。之前给出的定义是为一个 良好 的加密哈希函数而设的。但是什么使一个加密哈希函数成为 良好 的加密哈希函数呢？

良好的哈希函数是确定性的——相同的输入总会产生相同的输出。如果我对输入“baseball”进行哈希，那么，无论系统如何，那哈希函数每次都会输出相同的哈希。这在一定程度上也意味着，无论输入的大小，哈希的大小都将相同。这对处理效率和数据存储是重要的。知道唯一的输入总是会产生唯一的输出，并且这些输出始终是固定大小的，是良好加密哈希函数的明显指标。

良好的哈希函数是抗原像的。这意味着根据哈希逆向工程输入值在计算上是不可行的。因此，如果某人给你一个哈希，你就不能确定是什么数据产生了该哈希。这也引出了一个想法：两个不同的数据集不应产生相同的哈希。当任何两个输入 从不 产生相同的哈希时，良好的哈希函数被认为是抗碰撞的。

良好的哈希函数遵循雪崩效应——对输入的微小更改应该导致完全不同的哈希。即使更改一个字符也应该产生完全不同的哈希。因此，哈希输出不应透露任何关于输入的信息或有任何可识别的模式。注意上述图中的哈希差异。红狐狸“跑”的哈希与红狐狸“走”的哈希完全不同。这两个哈希中没有任何迹象表明它们包含几乎相同的信息。

良好的哈希函数应该是计算快速的。慢速哈希函数对于实时或接近实时的计算情况（例如交易验证）来说并不实用。慢速哈希函数可能成为严重的瓶颈，限制吞吐量和网络性能。快速哈希函数对于区块链的高效和安全性能是必要的。

为什么这对区块链很重要？

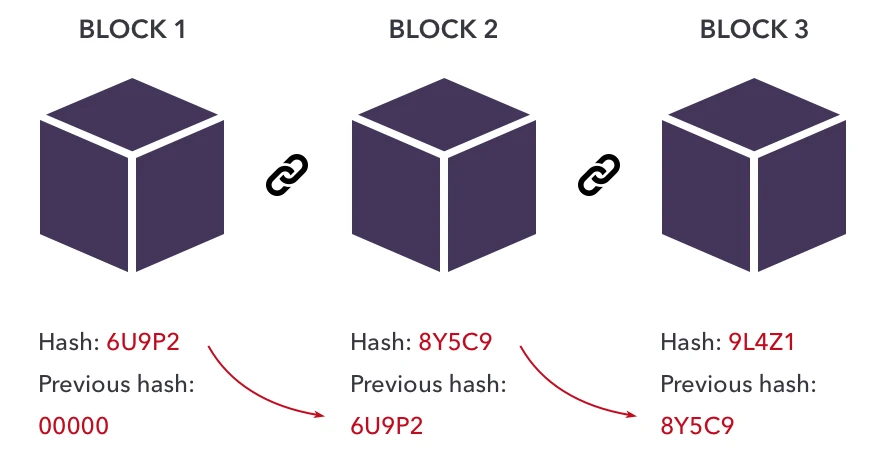
区块链是一个去中心化的、分布式的账本，记录其网络上的交易。这些交易被分组到区块中，这些区块通过 良好 的哈希函数安全链接在一起。每个区块包含交易数据、时间戳和前一个区块的哈希。由于每个区块的哈希依赖于上一个区块的哈希，任何对一个区块内容的更改都会改变其哈希并使所有后续区块失效。使用先前哈希生成新哈希的过程称为哈希链接。

向区块链添加新块被称为确认。确认验证并确保新块中的所有交易以及所有以前区块的安全性。这是因为每个新确认使得修改以前区块变得更加困难。要修改前一个区块，攻击者需要重新计算所有先前哈希。因此，哈希链接确保在一个区块获得一定数量确认后，篡改区块链是不可行的。

简单来说，区块链是一系列通过哈希函数安全链接的区块。但是，我们到底如何从一个区块指向另一个区块呢？是的，一个加密哈希函数用于链式连接这些块，但是我们如何能够查看之前区块的数据呢？我以为 良好 的加密哈希函数是抗原像的。

什么是哈希指针？

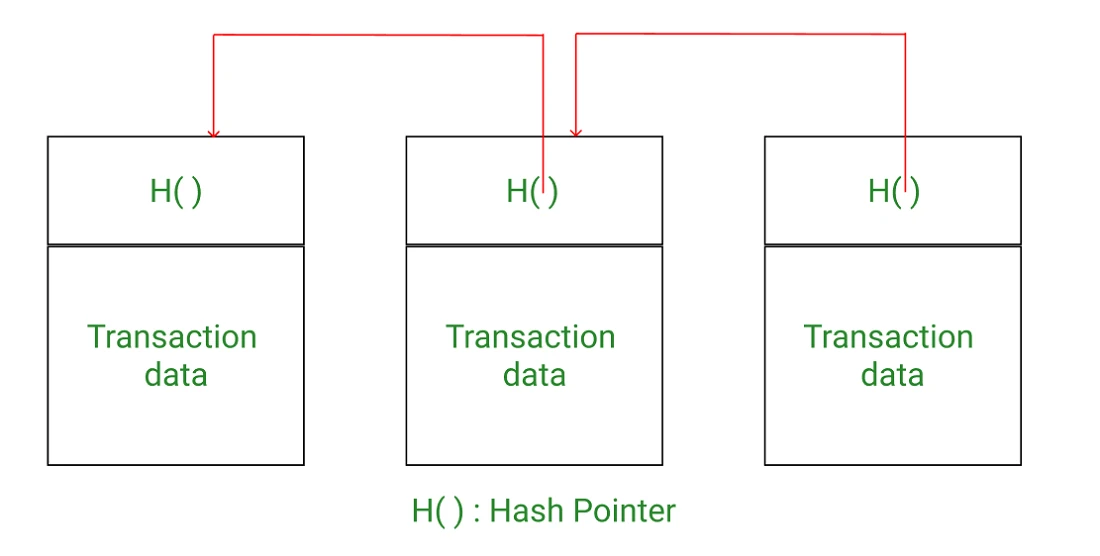
指针是一个变量，持有特定数据在内存中存储位置的位置。可以轻松访问该内存地址的数据，因为指针“指向”数据的位置。哈希指针是一种类似于指针的数据结构，但它还包含被引用数据的加密哈希。因此，哈希指针告诉你在哪里访问特定的数据，并允许你检查访问数据的完整性。

区块链的结构可以更准确地描述为使用哈希指针的链表。前一个区块的哈希是指向一组交易和这些交易所有哈希的哈希指针。哈希指针有助于区块链接、每个区块的完整性，并验证新添加的区块是否正确跟随前面的区块。

哈希指针用于有效地链接区块。但是区块中的交易呢？如果一个区块包含一千个交易，逐一验证这些交易不会很昂贵吗？

什么是默克尔树？

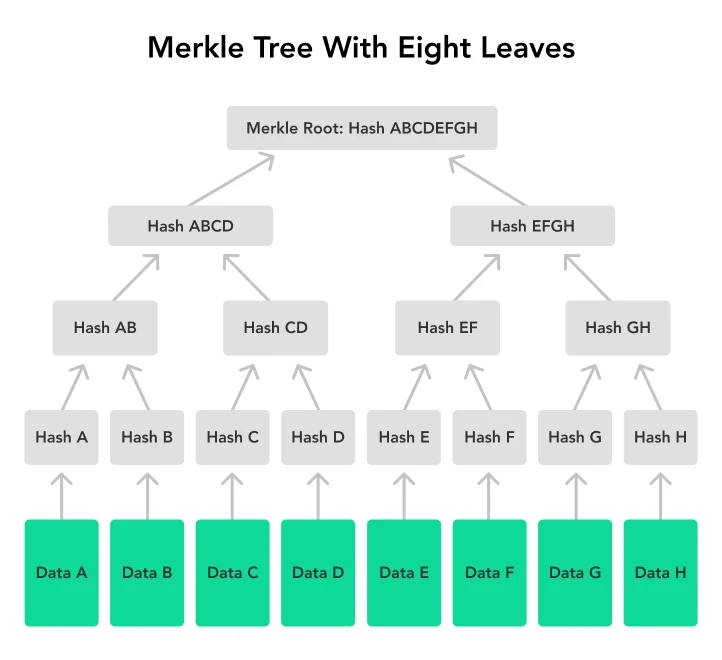
默克尔树是一种用于组织和验证大量数据的数据结构。这些数据被组织成一个树状结构，其中每个叶子或节点都用一组数据的哈希标记。每个非叶节点都是其子节点的哈希。默克尔树用于验证已传播到区块链的特定区块中包含的交易。那么，它是如何工作的呢？

交易被批量整理为列表以形成一个区块。列表中的每个交易使用一个 良好 的哈希函数进行哈希处理。这些哈希作为叶节点。这些叶节点成对哈希在一起以创建新的哈希层。这个过程通过迭代进行，直到只剩下一个被称为默克尔根的哈希。默克尔根存储在区块的头部，并作为该区块中所有交易的数字指纹。我们也可以将默克尔根称为区块的哈希。因此，当我们说一个新块与前一个块连接时，使用前一个块的块哈希时，我们的意思是该块使用前一个块的默克尔根作为新块哈希的一部分。

默克尔树高效地验证区块内的单个交易。传统上，你需要验证每个交易以验证特定交易，这非常昂贵并耗时。默克尔树提供了一个名为默克尔证明的加密“捷径”来帮助这一验证过程。默克尔证明是从交易的叶节点到底部的默克尔根的路径。参考上面的图像，想象这是从数据A到默克尔根的一条路径。这条路径还包括它的兄弟节点，路径上每个节点的相邻叶子节点，但不包括路径本身。验证者可以使用证明路径计算哈希，以检查其计算出的哈希是否与默克尔根匹配。如果结果哈希匹配，验证者就可以确信交易是合法的并且未被篡改。

通过对新叶的数据进行哈希并重新计算默克尔根，叶可以被更改。这个新的默克尔根用于验证新的更改，并使之前的证明失效。在像Solana这样高吞吐量的网络中，验证者可以快速接收对链上默克尔树的更改请求（例如，在同一槽内）。每个数据更改必须按顺序重新计算，否则每个后续更改请求都将被先前在该槽内进行的更改请求失效。在区块链中更改叶子数据和计算新的默克尔根非常常见。那么，我们如何解决快速更改的问题？

什么是并发默克尔树？

并发默克尔树是一种针对并发读写进行了优化的默克尔树。它存储最近更改的安全变更日志、其根哈希和证明。这些变更日志存储在链上特定于树的帐户中，并且在默克尔根仍然有效的情况下，可以更改的最大次数被称为 maxBufferSize。因此，当验证者快速接收到链上默克尔树的更改请求时，它可以使用该变更日志作为真相来源，允许最多 maxBufferSize 次更改在同一槽中。

并发默克尔树改进了传统的默克尔树，使其适合像Solana这样的高吞吐量环境。在Solana上创建链上并发默克尔树有以下三个属性影响树的大小、创建树的成本以及对树的并发更改次数：

• 最大深度
• 最大缓冲区大小
• 树冠深度

最大深度指的是从任何叶子到默克尔根所需的最大跳数。maxDepth用于确定树中要存储的最大节点数。可使用以下公式计算：numberOfNodes = 2 ^ maxDepth。树的深度必须在创建时设定，因此使用该公式确定你希望树存储多少个数据是重要的。

如前所述，最大缓冲区大小是指在其默克尔根仍然有效的情况下，可以对树进行的最大更改次数。

树冠深度指的是存储在链上的默克尔树的一个子集。这些缓存证明用于检查哈希是否与链上的默克尔根相匹配。在对叶子进行写入时，必须使用完整的证明路径来验证原始所有权。例如，在转让NFT时，你需要向树写入数据。树冠允许你减少证明大小，并避免使用 maxDepth 的证明大小来验证树。一个 maxDepth 为20的树将需要20的证明大小。而拥有15的树冠时，每次写入事务只需要提交5的证明大小。因此，更高的树冠深度会导致更高的前期成本，以便你在后续提交较小的证明。

树冠深度是创建树的成本的主要因素。这是因为树冠深度越高，所需的帐户就越大。开发者可以使用 @solana/spl-account-compression 包 来计算给定树大小所需的空间和在链上分配所需空间的成本。开发者可以使用 getConcurrentMerkleTreeAccountSize 函数根据参数计算给定帐户所需的空间，并使用 getMinimumBalanceForRentExemption 计算所需空间的最终花费，单位为Lamports。

Solana利用并发默克尔树进行状态压缩。状态压缩是生成离线数据哈希并将其存储在链上以便安全验证的方法。状态压缩的最流行用例是压缩NFT，因为它大幅减少了铸造的成本。例如，在Solana上铸造十亿个NFT的成本为507 $SOL，而使用“常规”NFT的成本为12,000,000 $SOL。现在你对哈希和默克尔树有了充分的了解，我们将在未来的文章中深入探讨压缩NFT！。

结论

祝贺你！在本文中，我们分析了哈希函数和默克尔树，这两个对区块链至关重要的加密原语。理解区块链并不是一件小事——它们是复杂的分布式系统，需要广泛的技术理解。通常，对于普通开发者、用户或投资者，这种知识是被假设的。本文不假设读者对加密原语有任何先前知识。相反，我们从基础开始，然后逐步深入讨论传统与并发默克尔树。拥有这些基本知识至关重要，因为它将使我们能够深入讨论更复杂的话题，例如压缩NFT。凭借这些新知识，你将能够更好地导航代码库或参与有关加密原语和更复杂加密解决方案的讨论。

如果你读到这里，谢谢你！

额外资源/进一步阅读

• 关于加密原语的详细书籍章节
• 比较安全哈希算法的文章
• Computerphile 的哈希算法与安全性 - YouTube 视频
• 关于默克尔树的简明 YouTube 视频
• 探索 Solana 上的 NFT 压缩

• 原文链接： helius.dev/blog/cryptogr...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～