Uniswap V2: 计算AMM交易的结算价格

这篇文章解释了如何确定自动做市商（AMM）中交易对的价格结算。它回答了“可以用多少代币 X 交换代币 Y 从 AMM 中？”这个问题。

在 Uniswap V2 上的 swap() 函数需要你提前计算从池中要交换的代币数量（包括 0.3% 的交易费用）。

考虑一个 ETH / USDC 的交易对，流动性池中有 100 ETH 和 100 USDC。为简化起见，这里假设 1 ETH 等于 1 USDC。

虽然 1 ETH 的现货价格是 1 USDC，反之亦然，但这并不意味着我们可以用 25 USDC 交换 25 ETH ，因为这不会保持 恒定乘积公式。

作者

本文由 Aymeric Taylor（LinkedIn，Twitter）共同撰写，他是 RareSkills 的一名研究实习生。

恒定乘积公式理论：x * y ≥ k

恒定乘积公式规定，在代币 X 和代币 Y 的对池中，池中两个资产数量的乘积（X 乘以 Y）在任何时候都应该保持恒定，至少不变。

$$x \times y \geq k$$

恒定乘积公式确保了两个代币之间的反比关系，建模市场的供需关系。随着一种代币数量的增加（存入 AMM），另一种代币的数量应减少（从 AMM 合约中提取）。

如果我们将变量重新排列，反比关系会更清楚地显示出来，如下方的等式所示。

$$y \geq \frac{k}{x}$$

让我们把运行示例代入恒定乘积公式方程：

• x 轴 = 100 ETH
• y 轴 = 100 USDC
• k = 10,000 (100 ETH * 100 USDC)
• 粉色线描绘了曲线 x y ≥ 10,000

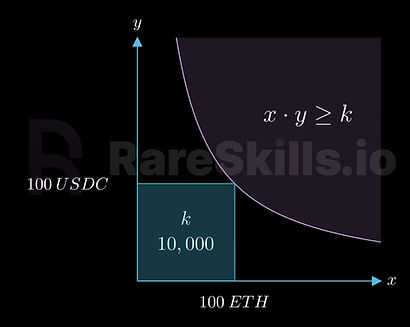
曲线下的框住区域是恒定的 k，即 x 和 y 的乘积。

我们稍后将演示如何以一种保持此常量的方式将 ETH 交换为 USDC。

Uniswap 恒定乘积公式实现

在实践中，恒定乘积公式是通过比较交易前后流动性池的恒定乘积来保证其至少保持不变。

$$k\text{before} \leq k\text{after}$$

Uniswap 不会阻止你给 AMM 提供超过你应给予的量，在这种情况下，如果你这样做，那么就是你低估了你能提取的量，因此出现了 ≤ 符号。

扩展上述等式，我们得到等效的方程如下：

$$\underbrace{x\text{Before} \times y\text{Before}}{k\text{Before}} \leq \underbrace{x\text{After} \times y\text{After}}{k\text{After}}$$

• x_Before 和 y_Before 是交换 前 流动性池中每种代币的数量。
• x_After 和 y_After 是交换 后 流动性池中每种代币的数量。

这意味着，交换 ETH 为 USDC 后，流动性池的恒定乘积必须至少保持不变。

$$\underbrace{\text{ETH}\text{Before} \times \text{USDC}\text{Before}}{k\text{Before}} \leq \underbrace{\text{ETH}\text{After} \times \text{USDC}\text{After}}{k\text{After}}$$

Uniswap V2 对每个交换收取 0.3% 的 AMM 交易费。在考虑费用时，流动性池的恒定乘积在每次交换之后都会增加。这种流动性的增长是流动性提供者的主要激励。只有在流动性提供者提取流动性时，池的恒定乘积才会减少。我们将展示如何在本文末尾计算包含交易费用的交换。

为什么我们不能用 25 ETH 交换 25 USDC

要确定一次交换是否合法，我们需要预先计算这次交换将如何影响流动性池的恒定乘积。它是否保持至少不变？

我们将 ΔETH 和 ΔUSDC 表示为分别存入和提取流动性池的数量。

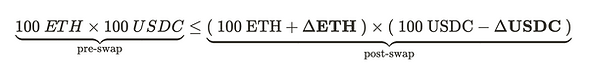
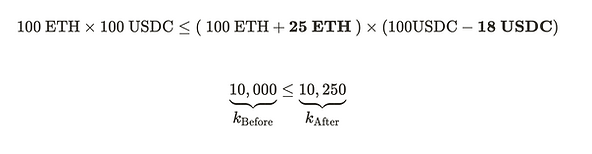
用 25 ETH 交换 25 USDC 意味着我们向 AMM 存入 25 ETH，并从中提取 25 USDC。这将调节流动性池的流动性到 125 ETH 和 75 USDC。AMM 将拒绝此交换，因为池的 恒定乘积 在交换后减少了。

交换后的产品低于交换前的产品 10,000，这违反了恒定乘积不变性。下图可视化该交换。

显然，我们无法期待提取 25 USDC——我们必须提取更少的量以保持恒定乘积不变。

确定正确的 USDC 交换金额

回到之前的例子，向池中添加 25 ETH 将 ETH 数量增加到 125 ETH（100 + 25）。接下来的任务是找到减少后的 USDC 数量，以保持恒定乘积，从而确保 AMM 会接受它。

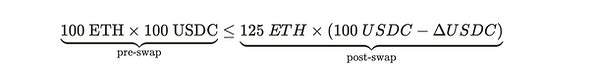
我们有一个方程揭示出可以交换 25 ETH 的最大 ΔUSDC 值。

求解 ΔUSDC

我们重新排列方程来明确求解 ΔUSDC。

此时池中有 125 ETH 和 80 USDC，总的恒定乘积为 10,000。

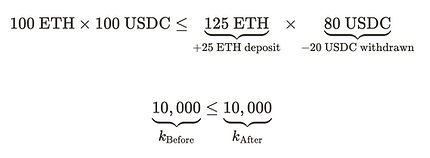
交换 25 ETH 换得 20 USDC 是你可以从 AMM 流动性池中提取的最多 USDC 数量。该交换被接受，因为它保持了恒定乘积公式。20 USDC 比 25 USDC 少五分之一，因此我们在此次交换中经历了滑点。滑点是由于我们的交易导致价格变动的程度。如果我们进行更小的交易，最终支付的价格接近 1 USDC : 1 ETH。但由于我们的交易量较大，最终支付的价格更高，提取的 USDC 更少，因此产生了更高的滑点。

我们可以在下面可视化此交换。

计算交换的通用公式可以表示如下：

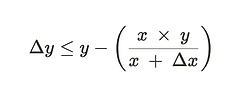
• x 和 y 表示交换前流动性池中的代币数量
• Δx 表示存入 AMM 的代币数量
• Δy 表示从 AMM 中提取的代币数量

错误计算交换：给 AMM 提供的超量

如果你提取更少的数量，例如 18 USDC，AMM 仍会接受，因为流动性池的恒定乘积增加，但你会因为没有最大化你的交换而遭受损失。

计算含费用的交换

我们上面进行了“理论”计算，这排除了交易费用。如前所述，Uniswap V2 对每次交换收取 0.3% 的交易费用，但费用仅适用于存入 AMM 的代币。假设我们用代币 X 交换代币 Y，0.3%的费用仅从 X 中扣除，而不从 Y 中扣除。

Uniswap V2 如何计算 0.3% 的费用是将存入的代币划分为两部分：

• 费用： 0.3%
• 可供交换的剩余量： 99.7%

对于 25 ETH，我们的费用和可供交换的剩余量将是：

• 费用（0.3%）： 0.075 ETH
• 可供交换的剩余量（99.7%）： 24.925 ETH

费用立即从此次交换的计算中排除，因此兑换者不会被记入 0.3% 的费用部分。

剩下的就是可供交换的数量，即 24.925 ETH。这就是我们从池中交换 USDC 的实际数量。

让我们求解可以从池中提取的最大 USDC 数量 (ΔUSDC)。向池中添加 24.925 ETH 会将 ETH 数量增加到 124.925 ETH。

求解 ΔUSDC 我们得到：

考虑到 0.3% 的交换费用，我们可以从 AMM 中提取大约 19.952 USDC。这比我们在没有费用的例子中能够获得的 20 USDC 要少。

计算时考虑费用的主要区别在于，我们将存入的代币乘以 99.7%，0.3% 被留出并分配给 AMM。给定 Δx 是存入的代币，Δy 是提取的代币数量，则一般方程变为：

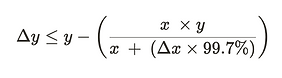
通过 RareSkills 学习更多

本文是我们高级 Solidity Bootcamp 的一部分。请查看课程以了解更多内容。

最初发布于 2024 年 4 月 17 日

• 原文链接： rareskills.io/post/unisw...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～