Monero技术详解(三):核心技术——环签名(1)
- victorsun
- 发布于 2020-06-18 15:55
- 阅读 9154
前文介绍了一次性地址,本文将以例子的形式来介绍Monero的核心技术——环签名
系列导航: Monero技术详解(一):技术方案总览 Monero技术详解(二):一次性地址 Monero技术详解(三):核心技术——环签名(1) Monero技术详解(四):隐藏交易数额之Pederson承诺
在前文介绍了Monero的一次性地址方案。从方案看来,Monero中的UTXO只有一次性地址,用户地址是产生一次性地址的基础,用户对UTXO的所有权并不能显现地看出来。发送人在每次交易时创建一次性地址来接收UTXO,并将一次性地址的相关私密信息(一次性私钥)秘密地传递给接收人,用以保护接收人隐私。这样,每个UTXO都具有不同的一次性地址,同一用户的不同笔UTXO“收入”都看上去没有联系。但是如果仅仅使用一次性地址,那么只要UTXO被花费出去,那么同一交易连接的输入输出的UTXO之间也可以产生联系,也就是说资金的链路还是没有被打断或者混淆,资金的走向还是清晰可见。
从观察者角度来看,每个UTXO可以看成与不同的用户对应。如果发送人在发送交易的时候引入多个UTXO,并且将真正的UTXO混淆与引入的UTXO集合之中,这样观察者追踪资金链路的难度将会加大。多次交易之后资金的追踪将会是实际上不可行。那么问题出现了,如何将多个UTXO涉及的一次性地址“捆绑”在一起呢?这里需要使用到环(群)签名方案。
1. 环签名概念介绍
将真正签名人隐藏于多个“助攻”签名人集合之中这一想法最早起源于群签名,在群签名之中存在分发中心,分发中心不仅负责分发产生与分发密钥,并且有机制可以恢复出真正的签名人。但是在环签名中,分发中心被彻底取消。用户密钥不需要分发,只要用户自己生成,也无法恢复出真正的签名人身份。
具体来说,环签名具有如下几个性质:
- 签名人混淆性质:旁观者只能确定签名出自于群体中的某一成员,仅此而已,具体何人,无从得知,
- 可链接性:如果同一私钥对不同的消息进行签名,那么有算法可以判定这两个签名出自于同一私钥只手。这种可链接性可与群体有关系,也可与群体无关系。与群体有关系是指,两个环签名所选的混淆群体不同,那么可能无法获知两个环签名是否出自于同一私钥。与群体无关系,就是说无论两个环签名算选的混淆群体是否相同,那么只要这两个环签名出自于同一私钥,就可以链接起来。
- 不可伪造性:没有私钥不能伪造一个合法的环签名。
虽然环签名概念本身与Monero并无关系,但是这里依然用Monero的场景来举例说明某几个环签名方案。
2. Version-1: 绑定群体的可链接性
2.1 方案
以3个UTXO作为混淆输入为例。假设发送人Alice拥有某一UTXO,其一次性地址为$K^a_2 \rightarrow K_2$,其对应的一次性私钥是$k^a_2 \rightarrow k_2$。并且假设交易发送给Bob且是单输出(此处多输出并无不同)。Alice同时选择3个一次性地址$K_1,K_3,K_4$(不需要拥有其对应的私钥),组成环$\mathcal{R} = {K_1,K_2,K_3,K_4}$,接下来Alice如下步骤操作来签名交易信息$msg$:
-
利用自己掌握的私钥$k_2$作:$\tilde{K} \leftarrow k_2\mathcal{H}_p(\mathcal{R})$;// $\mathcal{H}_p(\mathcal{R})$是椭圆曲线上的点
-
产生随机数$\alpha$与$r_1,r_3,r_4$;// 不产生$r_2$
-
计算“签名环”的“接头点” $$ c_3 \leftarrow \mathcal{H}_n(\mathcal{R}, \tilde{K}, msg, \alpha G, \alpha \mathcal{H}_p(\mathcal{R})) $$
-
逐步“编织”签名环: $$ D_4 \leftarrow r_3G + c_3K_3, \ \ \ E_4 \leftarrow r_3\mathcal{H}_p(\mathcal{R}) + c_3\tilde{K}, \ c_4 \leftarrow \mathcal{H}_n(\mathcal{R}, \tilde{K}, msg, D_4, E_4) $$
$$ D_1 \leftarrow r_4G + c_4K_4, \ \ \ E_1 \leftarrow r_4\mathcal{H}_p(\mathcal{R}) + c_4\tilde{K}, \ c_1 \leftarrow \mathcal{H}_n(\mathcal{R}, \tilde{K}, msg, D_1, E_1) $$
$$ D_2 \leftarrow r_1G + c_1K_1, \ \ \ E_2 \leftarrow r_1\mathcal{H}_p(\mathcal{R}) + c_1\tilde{K}, \ c_2 \leftarrow \mathcal{H}_n(\mathcal{R}, \tilde{K}, msg, D_2, E_2) $$ //其中$\mathcal{H}_n(\mathcal{R}, \tilde{K}, msg, D_2, E_2)$是数域上的标量
-
“焊接”首尾成为签名环: $$ r_2 \leftarrow \alpha - c_2k_2 $$
输出结果签名$\sigma(msg) = (c_1, r_1, r_2, r_3, r_4)$,密钥像$\tilde{K}$($\tilde{K}$实际上是对真正签名人信息和用于混淆的所有公钥信息的承诺),以及成员集合$\mathcal{R}$。
2.2 验签
验签过程实际上就是从起点(并不一定是签名人的“起始点”)开始,依次验证签名环中相邻的两个节点之间是否满足“编织”的映射关系,并最终是否能回到起始点。
形式化地描述,对于签名$\sigma = (c_1, r_1, r_2, r_3, r_4)$、密钥像$\tilde{K}$、消息$msg$、公钥集合$\mathcal{R} = {K_1,K_2,K_3,K_4}$,令依次验证: $$ D_2' \leftarrow r_1G + c_1K_1, \ \ \ E_2' \leftarrow r_1\mathcal{H}_p(\mathcal{R}) + c_1\tilde{K}, \ c_2' \leftarrow \mathcal{H}_n(\mathcal{R}, \tilde{K}, msg, D_2', E_2'), \ \ \ c_2' == c_2 $$
$$ D_3' \leftarrow r_2G + c_2K_2, \ \ \ E_3' \leftarrow r_2\mathcal{H}_p(\mathcal{R}) + c_2\tilde{K}, \ c_3' \leftarrow \mathcal{H}_n(\mathcal{R}, \tilde{K}, msg, D_3', E_3'), \ \ \ c_3' == c_3 $$
$$ D_4' \leftarrow r_3G + c_3K_3, \ \ \ E_4' \leftarrow r_3\mathcal{H}_p(\mathcal{R}) + c_3\tilde{K}, \ c_4' \leftarrow \mathcal{H}_n(\mathcal{R}, \tilde{K}, msg, D_4', E_4'), \ \ \ c_4' == c_4 $$
$$ D_1' \leftarrow r_4G + c_4K_4, \ \ \ E_1' \leftarrow r_4\mathcal{H}_p(\mathcal{R}) + c_4\tilde{K}, \ c_1' \leftarrow \mathcal{H}_n(\mathcal{R}, \tilde{K}, msg, D_1', E_1'), \ \ \ c_1' == c_1 $$
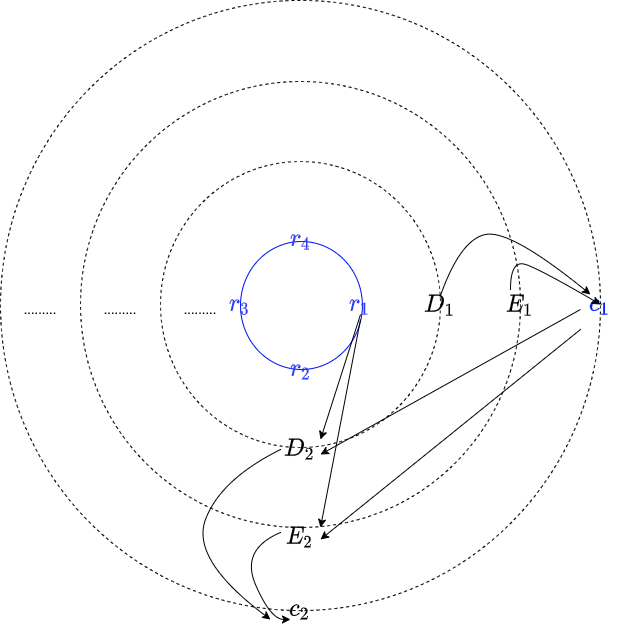
2.3 解释
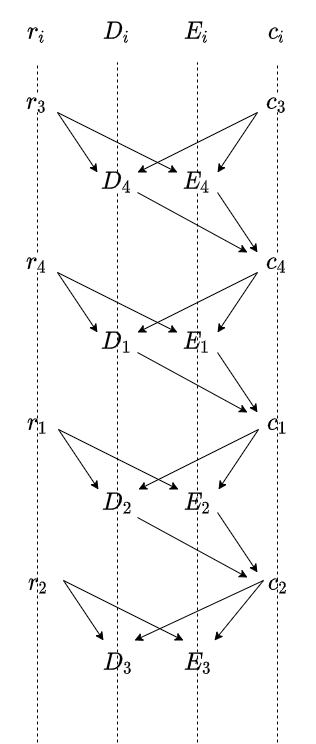
将以上的方案图式化如上图。签名环从接头点——第三个节点着手,开始编织签名环。从上一个节点到下一个节点通过3个映射关系连接起来。结合随机数,计算这个三个映射关系,得到下一个签名环节点。按此方式编织下去,得到一个“签名带”,需要将签名带的首尾焊接起来,获得一个完整的环状结构。如果在没有部分私密信息的情况下,签名带只能一直向下编织,而不能回头与起始点衔接,因为从例子可以看出,从$D_3$和$E_3$映射出来的$c'_3 \leftarrow \mathcal{H}_n(\mathcal{R}, \tilde{K}, msg, D_3, E_3)$(为了与起点的$c_3$区别,记作$c'_3$)不能与起点的$c_3$相同,所以首尾连接失败。但是幸亏在起始点上拥有“陷门”信息——私钥$k_2$。具体的做法:
起始点:$c_3 = \mathcal{H}_n(\mathcal{R}, \tilde{K}, msg, \alpha G, \alpha \mathcal{H}_p(\mathcal{R}))$
结尾点:$c'_3 \leftarrow \mathcal{H}_n(\mathcal{R}, \tilde{K}, msg, D_3, E_3)$,且$D_3 = r_2G + c_2K_2$,$E_3 = r_2\mathcal{H}_p(\mathcal{R}) + c_2\tilde{K}$
如果要让$c_3 = c'_3$,需要让 $$ \alpha G = r_2G + c_2K_2 = (r_2+c_2k_2)G $$
$$ \alpha \mathcal{H}_p(\mathcal{R}) = r_2\mathcal{H}_p(\mathcal{R}) + c_2\tilde{K} = (r_2+c_2k_2)\mathcal{H}_p(\mathcal{R}) $$
在产生随机数${r_i}$时刻意没有产生随机的$r_2$,取而代之的是$\alpha$,这让签名环的收尾衔接有了可能。要让以上两等式成立,只需可以巧妙拼凑$r_2$来达到目的。这里令$r_2\leftarrow \alpha - c_2k_2$即可。
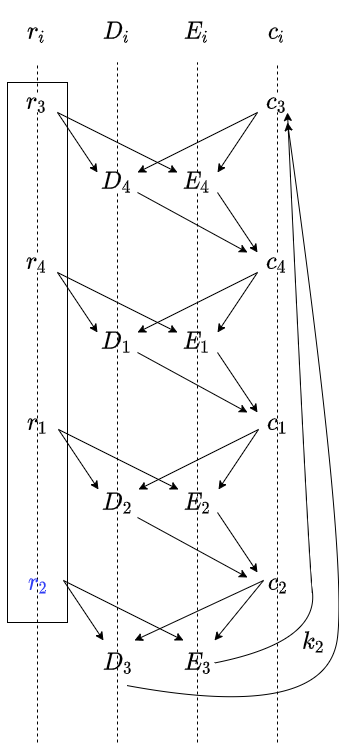
这种预先埋陷门的方式,让带状结构首尾衔接成了完整的环状结构,并且从签名环看来,无法看出签名的起点(起点即是真正的签名人)。
2.4 问题
如上所说,环签名需要有可链接性,即当同一私钥对不同消息$msg_1$和$msg_2$分别作出两个不同的签名$\sigma_1$和$\sigma_2$时,这两个签名就是链接起来的。在Monero中,如果发现同一UTXO的私钥作了两个不同的签名,说明该UTXO有被双花的恶意。有一笔交易将被判定为非法。上述方案的可链接性需要用于混淆两个签名的参与者集合也相同才可以(实际使用中,通过判定密钥像$\tilde{K}$是否曾经出现过来判断UTXO是否双花),但是恶意的发送中用不同的签名者集合就会逃过这一检查。本方案对于用户量少且固定的场景较为合适,因为这样可以将所有的用户公钥都作为混淆个体。当用户不固定时将不具有可链接性。Monero中每个UTXO对应一个(一次性)公钥,所以以上方案对于Monero并不适用。
3. Version-2: 独立于群体的可链接性
为了让发送者在选择不同的群体时也不能发动双花交易,需要让环签名方案拥有的独立于群体的可链接性,即无论签名者在两次签名所使用的混淆集合是否相同,只要真正签名人相同,那么着两个签名就可以判定为是同一个签名人所为。为此,可以将Version-1的方案中的密钥像$\tilde{K}$替换成只与签名人有关的信息(Version-1中$\tilde{K}$包含的是真正签名人信息和用于混淆的所有公钥信息)——$\tilde{K} \leftarrow k_2\mathcal{H}_p(K_2)$作为密钥像。其他细节与Version-1几乎相同,也是从起始点“编织”签名带,再利用真正的私钥作为陷门将签名带的结尾与起始点巧妙焊接。
3.1 方案
同样以Version-1的场景为例描述方案。
-
利用自己掌握的私钥$k_2$作:$\tilde{K} \leftarrow k_2\mathcal{H}_p(K_2)$;
-
产生随机数$\alpha$与$r_1,r_3,r_4$;// 不产生$r_2$
-
计算“签名环”的“接头点” $$ c_3 \leftarrow \mathcal{H}_n( msg, \alpha G, \alpha \mathcal{H}_p(K_2)) $$
-
逐步“编织”签名环: $$ D_4 \leftarrow r_3G + c_3K_3, \ \ \ E_4 \leftarrow r_3\mathcal{H}_p(K_2) + c_3\tilde{K}, \ c_4 \leftarrow \mathcal{H}_n( msg, D_4, E_4) $$
$$ D_1 \leftarrow r_4G + c_4K_4, \ \ \ E_1 \leftarrow r_4\mathcal{H}_p(K_2) + c_4\tilde{K}, \ c_1 \leftarrow \mathcal{H}_n(msg, D_1, E_1) $$
$$ D_2 \leftarrow r_1G + c_1K_1, \ \ \ E_2 \leftarrow r_1\mathcal{H}_p(K_2) + c_1\tilde{K}, \ c_2 \leftarrow \mathcal{H}_n(msg, D_2, E_2) $$ //其中$\mathcal{H}_n(msg, D_2, E_2)$没有在像Version-1中把环成员$\mathcal{R}$和密钥像$\tilde{K}$纳入其中。
-
“焊接”首尾成为签名环: $$ r_2 \leftarrow \alpha - c_2k_2 $$
输出结果签名$\sigma(msg) = (c_1, r_1, r_2, r_3, r_4)$,密钥像$\tilde{K}$,以及成员集合$\mathcal{R}$。
验签过程与Version-1几乎相同。
4. Version-3: 简单的多UTXO输入版本
以上的两个方案都都是要发送单个UTXO。发送人都是以私钥为$k_2$,公钥为$K_2$的UTXO为输入来组织交易的环签名的。但是实际中发送人需要组织多个UTXO的环签名。
例如发送人拥有2个UTXO,对应的公私钥对分别是$UTXO1:(K{1,2}, k_{1,2})$、$UTXO2:(K{2,3}, k_{2,3})$。可以对每个UTXO,运用 Version-2的方案构建独立的环签名放入到交易中。但是这样的问题是,环签名的数量与输入的UTXO数量成线性增长,这使得交易数据的空间复杂度与签名、验签的时间复杂度都成线性增长,有优化的空间。
总之,真正的签名人,“编织”签名带,并且最终,运用自己所具有的私钥作为“焊接”器,讲编织带的收尾完美地焊接起来。使之成为一个外观完美的环。
环签名的作用不仅仅可以用来混淆发送者,还可以用来作资金数额的区间证明,这个将在后续文章介绍。
- 回归密码朋克——2. 每个人都可以,天生就是密码朋克 475 浏览
- Galaxy Research:美联储官员讲话、HeavenDEX 崛起及门罗币 51% 攻击分析 883 浏览
- 区块链 101:区块链之旅 3253 浏览
- 范围证明 2484 浏览
- 隐私货币:第一部分 848 浏览
- 隐私币为何没有兴起 1508 浏览
- Monero技术详解(四):隐藏交易数额之Pederson承诺 6975 浏览
- Monero技术详解(二):一次性地址 7800 浏览
- Monero技术详解(一):技术方案总览 7737 浏览
- 何谓“零知识”,何谓“证明”? 3646 浏览

