释放ElGamal加密的力量 - 使用SageMath实现和增强安全性

• 简介
• ElGamal 加密
• 增强 ElGamal 加密的安全性
• 寻找安全生成器
• ElGamal 加密的实际应用
• 结论

介绍

ElGamal 加密是一种广泛使用的公钥加密算法，为通信系统提供保密性和安全性。它由 Taher ElGamal 于 1985 年提出，基于 Diffie-Hellman 密钥交换协议。在本指南中，我将逐一讲解 ElGamal 加密方案的关键组成部分，包括密钥生成、加密和解密。我还将演示如何使用 SageMath 软件实现该算法，并通过使用 256 位随机质数来增强系统的安全性。

ElGamal 加密

关键组件 ElGamal 加密方案由三个主要组件组成：

• 密钥生成：为加密和解密过程生成一对公钥和私钥的过程。
• 加密：使用公钥将明文转换为密文的过程。
• 解密：使用私钥从密文中恢复明文的过程。

在 ElGamal 加密中，公钥用于加密消息，而私钥用于解密。ElGamal 加密方案的安全性基于求解离散对数问题的难度。

让我们考虑一个 ElGamal 加密过程的示例：

• Alice和Bob同意一个大质数 $p$ 和一个原根 $g$（模 $p$）。
• Bob选择一个随机私钥 $x$，并计算他的公钥 $Y = g^x \mod p$。
• Alice想把一个消息 $M$ 发送给Bob。她选择一个随机整数 $k$ 并计算密文 $(a, b) = (g^k \mod p, M * Y^k \mod p)$。
• Bob接收密文，并使用他的私钥解密：$M = b * a^{-x}\ mod\ p$。

ElGamal 加密的流程

这里是 ElGamal 加密的完整流程图。

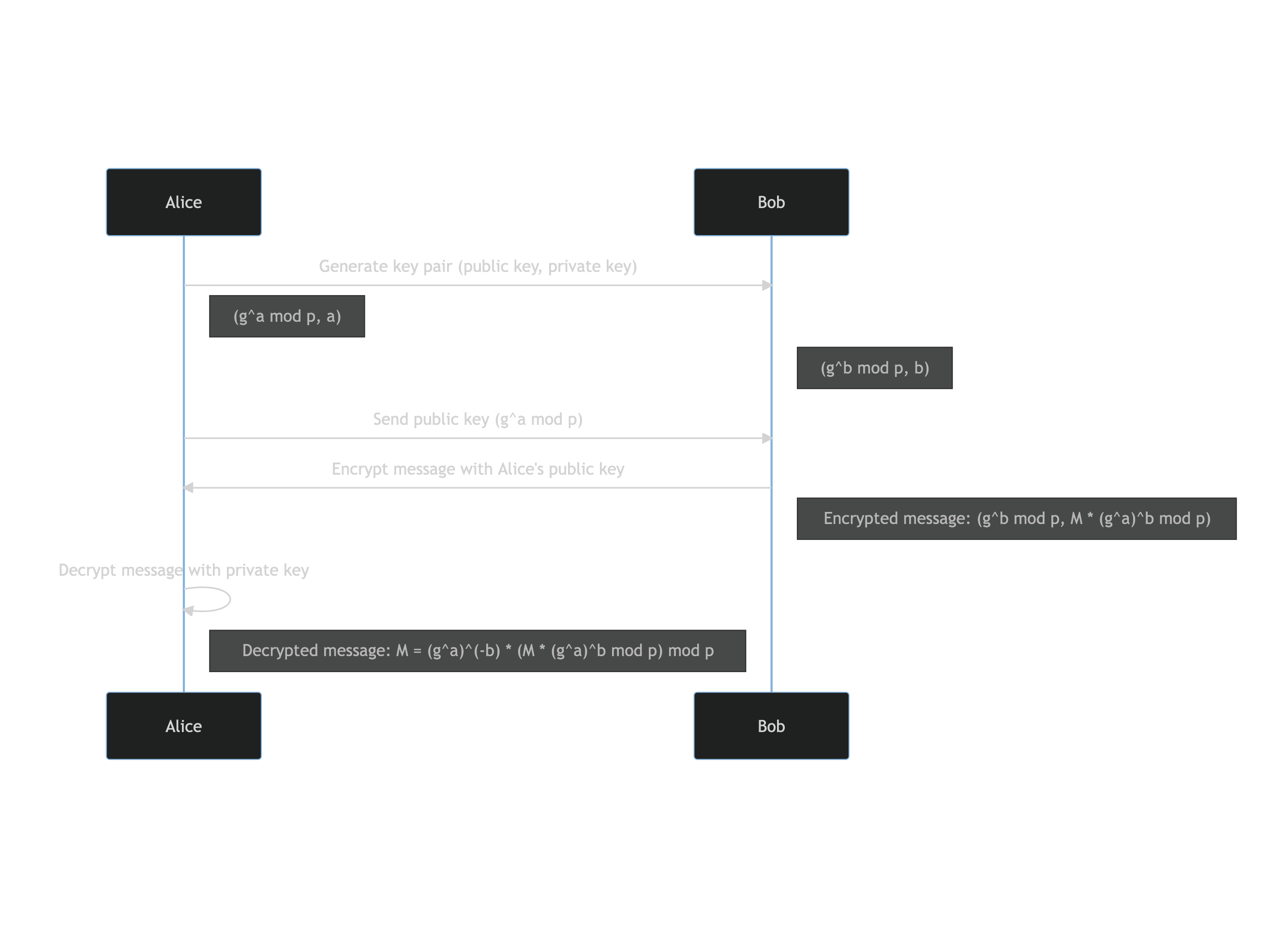
sequenceDiagram 

Alice->>Bob: 生成密钥对（公钥，私钥） 
Note right of Alice: (g^a mod p, a) 
Note right of Bob: (g^b mod p, b) 
Alice->>Bob: 发送公钥 (g^a mod p) 
Bob->>Alice: 使用Alice的公钥加密消息 
Note right of Bob: 加密消息: (g^b mod p, M * (g^a)^b mod p) 
Alice->>Alice: 使用私钥解密消息 
Note right of Alice: 解密消息: M = (g^a)^(-b) * (M * (g^a)^b mod p) mod p

使用 SageMath 实现 ElGamal 加密 SageMath 是一个开源数学软件，为实现各种加密算法（包括 ElGamal 加密）提供了强大的环境。要开始使用 SageMath，你可以在本地机器上安装它，或使用可在 sagemath.org 上获得的在线版本。

安装并运行 SageMath 后，你可以按如下操作实现 ElGamal 加密过程：

   from sage.all import *

   # 密钥生成
   p = 23  # 质数
   g = 5   # 生成器
   x = 6   # Bob的私钥
   Y = power_mod(g, x, p)  # Bob的公钥

   # 加密（Alice）
   M = 12  # 消息
   k = 3   # 随机值
   a = power_mod(g, k, p)
   b = (power_mod(Y, k, p) * M) % p

   # 解密（Bob）
   M_decrypted = (b * power_mod(a, -x, p)) % p

   print("原始消息:", M)
   print("加密消息:", (a, b))
   print("解密消息:", M_decrypted)

此示例演示了具有固定质数 $p$ 的基本 ElGamal 加密过程。输出显示原始消息、加密消息和解密消息。

增强 ElGamal 加密的安全性

选择 256 位随机质数 在 ElGamal 加密过程中使用大质数对于确保系统的安全性至关重要。较大的质数使攻击者更难解决离散对数问题，这是 ElGamal 加密方案安全性的基础。

要在 SageMath 中生成 256 位随机质数，你可以使用 random_prime() 函数：

   p = random_prime(2^256, lbound=2^255, proof=False)  # 256 位质数

通过使用这种新的质数生成方法更新之前的 SageMath 代码，你可以增强 ElGamal 加密过程的安全性。

寻找安全生成器

在 ElGamal 加密方案中，选择一个安全生成器 $g$ 对于系统的安全性至关重要。安全生成器是一个能够生成乘法群 $modulo p$ 的循环子群的数字，其中 $p$ 是一个大质数。

要找到一个安全生成器 $g$，请遵循以下步骤：

1. 首先，选择一个大质数 $p$，并计算 $(p-1)/2$，该值也应该是质数。这个新质数称为 $q$。
2. 现在，从集合 ${2, 3, ... , p-2}$ 中选择一个随机数 $g$。
3. 计算 $(g^q) \mod p$。如果结果不等于 1，则 $g$ 是一个安全生成器。

以下是如何使用 SageMath 找到安全生成器的示例：

## 为给定质数 $p$ 找到安全生成器 $g$
def find_safe_generator(p):
    q = (p - 1) // 2
    g = 2
    while True:
        if power_mod(g, q, p) != 1:
            return g
        g += 1

## 示例：为 256 位质数找安全生成器
p = random_prime(2^256, 2^255)
g = find_safe_generator(p)
print("安全生成器 (g):", g)

通过遵循此方法，你可以确保所选择的生成器 $g$ 是安全的，并适合在 ElGamal 加密方案中使用。

ElGamal 加密的实际应用

ElGamal 加密有许多实际应用，包括：

• 安全通信：ElGamal 加密可用于确保通信系统（如电子邮件和即时消息）的保密性。
• 数字签名：ElGamal 加密可以改编用于数字签名方案，为电子文档和交易提供完整性和不可否认性。
• 密钥交换：ElGamal 可以用作密钥交换协议，允许双方在不安全的通道上建立共享密钥。
• 安全投票系统：ElGamal 加密可用于安全电子投票系统，以维护选民隐私并确保投票的准确计数。

尽管有其益处，但 ElGamal 加密在选择加密解决方案时也有一些局限性：

• 计算复杂性：ElGamal 加密和解密需要模幂运算，这在处理大质数时可能计算上比较昂贵。
• 消息扩展：ElGamal 加密中的密文由两个元素组成，与原始明文大小相比，导致消息扩展因子为二。
• 缺乏内置认证：ElGamal 加密不提供内置的信息认证或完整性检查，可能需要额外的机制来确保数据完整性。

结论

在这篇文章中，我提供了对 ElGamal 加密及其关键组成部分的深入解释，包括密钥生成、加密和解密。我还演示了如何使用 SageMath 实现 ElGamal 加密算法，并通过使用 256 位随机质数来增强系统的安全性。

ElGamal 加密是密码学领域的一项重要工具，在安全通信、数字签名、密钥交换和安全投票系统等多个实际应用中具有重要作用。然而，考虑到其局限性，选择最合适的加密方案以满足你的具体需求至关重要。

我鼓励你使用 SageMath 进行 ElGamal 加密实验，并探索其在各种应用中的潜力。通过了解 ElGamal 加密的基本原理及其实现，你可以构建更安全、更可靠的加密系统。

你可以在 GitHub 仓库找到完整代码 github.com/thogiti。

参考文献

1. ElGamal, T. (1985). 基于离散对数的公钥密码系统和签名方案。IEEE 信息理论学报, 31(4), 469-472.
2. Diffie, W., & Hellman, M. E. (1976). 密码学的新方向。IEEE 信息理论学报, 22(6), 644-654.

• 原文链接： github.com/thogiti/thogi...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～