AMM中的路由革命 - Uniswap V4中的Hook与最佳交易执行 - 一篇论文评审

对于熟悉 Uniswap 的人来说，你会知道它的力量在于其简单性：由常数函数市场制造商（CFMM）公式管理的流动性池。最近，Uniswap V4 引入了 Hooks，这是一种智能合约“扩展”，能够将自定义逻辑注入到这些池中。想象一下：动态费用根据波动性调整，在 AMM 直接进行链上限价单，以及市场对外部数据源的反应。Hooks 准备解锁 DeFi 市场的新水平的复杂性和定制化。

最近一篇由 Tarun 等人撰写的论文，“在 Hooks 存在下的最优路由：三个案例研究,” 深入探讨了 hooks 对最优交易路由的影响。

这篇论文探讨了一个关键问题：在这个新景观中，我们如何在增强了 hooks 的 CFMM 中优化交易路由？作者提供了严格的数学框架和三个有见地的案例研究。

总体而言，论文表明，这些新设计的 hooks——限价单、时间 hooks 和外部（“主权”）hooks——都可以通过标准数学技术（凸优化, 马尔可夫决策过程）和数值分析整合到 CFMM 路由中。结果是，交易在链上的执行设计空间更为丰富，超越了早期 CFMM 静态的“一次性”交易。

关键要点

• 在大多数 hooking 场景中，当 hook 以凹/凸方式修改 输出集 时，凸性是保留的（例如，限价单）。
• 当交易分摊到不同时间，并存在路径依赖或状态依赖优势时，动态规划是必不可少的（例如，捕捉有利的错误定价）。
• 均值-方差风格的框架捕获来自不确定、不可组合 hooks 的风险。

CFMM 和最优路由问题的背景

常数函数市场制造商 (CFMMs)

一个 常数函数市场制造商 是一个持有两个资产 $A$ 和 $B$ 的非负储备 $R, R'$ 的智能合约。用户可以提交一个交易 $\bigl(\Delta,\Delta'\bigr)$（意味着用户输入 $\Delta$ 个单位的 $A$ 以换取 $\Delta'$ 个单位的 $B$），该交易在满足 交易函数 $\varphi$ 时被接受。例如，一个常数乘积 CFMM 使用

$$ \varphi(R, R', x, y) \;=\; (R + x)\,(R' - y) \;=\; K, $$

其中 $K$ 在没有交易发生时是固定的。用户接收的输出 $\Delta'$ 是通过 $\varphi$ 隐式确定的。

正向交换函数

一个关键概念是 正向交换函数 $G(\Delta)$。对于特定的 CFMM，在储备 $(R, R')$ 和资产 $A$ 的交易大小 $\Delta$ 下：

• $G(\Delta)$ 是用户收到的净 $B$ 的数量。
• 等价地，可以将边际交换率 $g(\Delta)$ 定义为 $\Delta'$ 对应于 $\Delta$ 的导数。
• 在大多数标准 CFMM（如常数乘积或常数和）中，$G$ 是凹且递增的，反映了较大输入交易的收益递减。

原始路由问题

给定一个 $m$ 个 CFMM 和 $n$ 个资产的 网络，用户希望找到一个最佳净交易 $\Psi$（在所有 $n$ 个资产中）以最大化某个效用 $U(\Psi)$。每个 CFMM $i$ 有一个可行的 交易集 $T_i$。经典问题是

$$ \begin{aligned} \text{maximize}\quad &U(\Psi),\ \text{subject to}\quad &\Psi \;=\; \sum_{i=1}^m A_i\, \Delta_i,\quad \Delta_i \;\in\; T_i, \end{aligned} $$

其中 $A_i$ 是局部与全局的“资产索引”矩阵，而 $\Delta_i$ 表示市场 $i$ 中的交易。由于每个 $T_i$ 通常是一个 凸 集（来自于凹 CFMM 不变性），因此可在 $\Psi,\Delta_i$ 中获得一个凸程序。

由 Diamandis et al. (2023) 引入了一种高效分解算法来解决这个路由问题。在实践中，流行的 DEX 聚合器（如 1inch、Matcha、Uniswap 自身的路由器等）在寻找多池路由时，通常会解决这个问题的近似版本。

在 Hooks 存在下的路由

一个 hook 是一个特殊的智能合约，能够修改或扩展 CFMM 的行为，例如动态改变费用、添加外部流动性条件或引入外部数据。Uniswap v4 提出了一个设计，允许在池的生命周期中 各个阶段 轻松扩展此类自定义逻辑。

这篇论文将关注三种改变路由问题的 archetypal hooks：

• 链上限价单，它们表现为离散价格的“额外流动性”。
• 将用户交易（清算）分布在时间上的 hooks，利用外部波动性。
• 提供更好价格但附带填充风险的非可组合 hooks。

在每种情况下，作者都制定了新的优化或动态编程模型，并展示如何解决这些问题。

通过限价单进行路由

限价单作为交易集

从路由器的角度来看，限价单 是：

• 最大（买入）或最小（卖出）价格 $p_0$。
• 最大交易量 $V_0$。

从数学上讲，假设用户在卖出 $A$ 以获得 $B$，则（买入）限价单是集合

$$ \tilde{T} \;=\; \bigl{(z^1,z^2)\,\mid\,z^2 \le p_0\,z^1,\;z^2 \le V_0,\;z^1,z^2 \ge 0\bigr}. $$

因为这个区域是由线性（不等）式定义的，它是凸的。多个限价单可以被 Minkowski 求和 成单个的组合可行集。

修改后的正向交换函数

当一个限价单与标准的 CFMM 曲线 $G(\Delta)$ 组合时，用户有时可以在价格 $p_0$ 停止 CFMM 交易，直到使用了交易量 $V_0$，从而形成一个新的分段函数 $\tilde{G}(\Delta)$。这个函数：

• 在 CFMM 的 瞬时价格 达到 $p_0$ 之前遵循 CFMM 的原始 $G(\Delta)$。
• 然后成为以斜率 $p_0$ 的 线性 形式（即，限价单“主导” CFMM）直到点 $\Delta_2$ 的位置，在该位置限价单被完全使用。
• 最后，如果 $\Delta$ 超过 $\Delta_2$，则继续按照 CFMM 的原始曲线进行。

我们可以用分段形式写出新的正向交换函数 $G_{\text{with-limit}}$：

$$ G{\text{with-limit}}(\Delta) \;=\; \begin{cases} G{\text{CFMM}}(\Delta), & \Delta\le \Delta1,\[4pt] G{\text{CFMM}}(\Delta_1) + p_0 \,(\Delta - \Delta_1), & \Delta_1<\Delta\le \Delta_2,\[4pt] \ldots \end{cases} $$

其中 $\Delta_1$ 是 CFMM 的边际价格首次达到 $p_0$ 的位置，而 $\Delta_2$ 是限价单被完全消耗的点。可以证明这个分段函数仍然是凹的且单调递增的，因此 $\tilde{T}$ 仍维持凸性。这意味着，使用限价单的最优路由仍然是一个凸问题。

该方法产生一个分段定义的、凹的函数，在过渡边界 $\Delta_1$ 和 $\Delta_2$ 处可微。

使用限价单解决路由问题

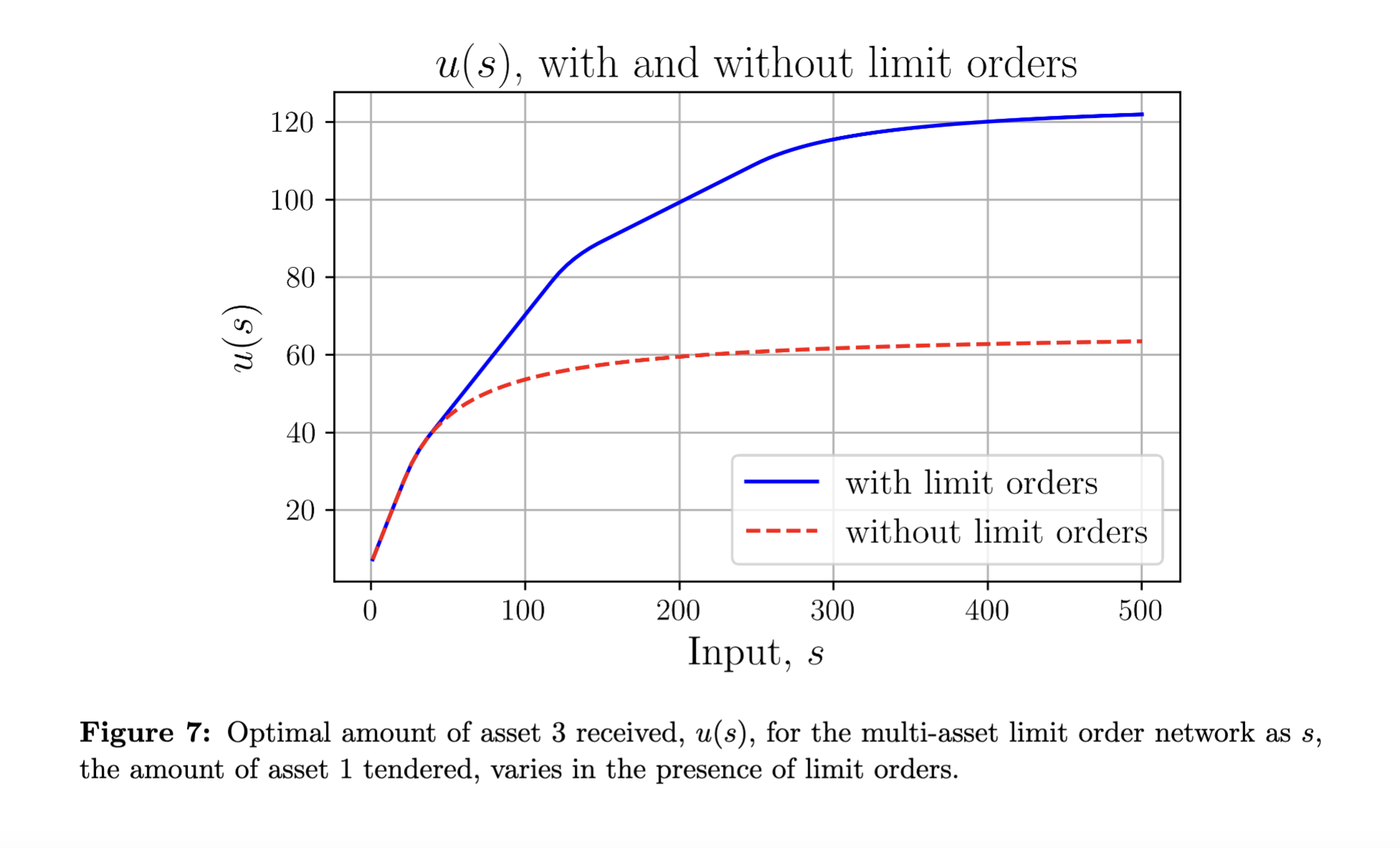
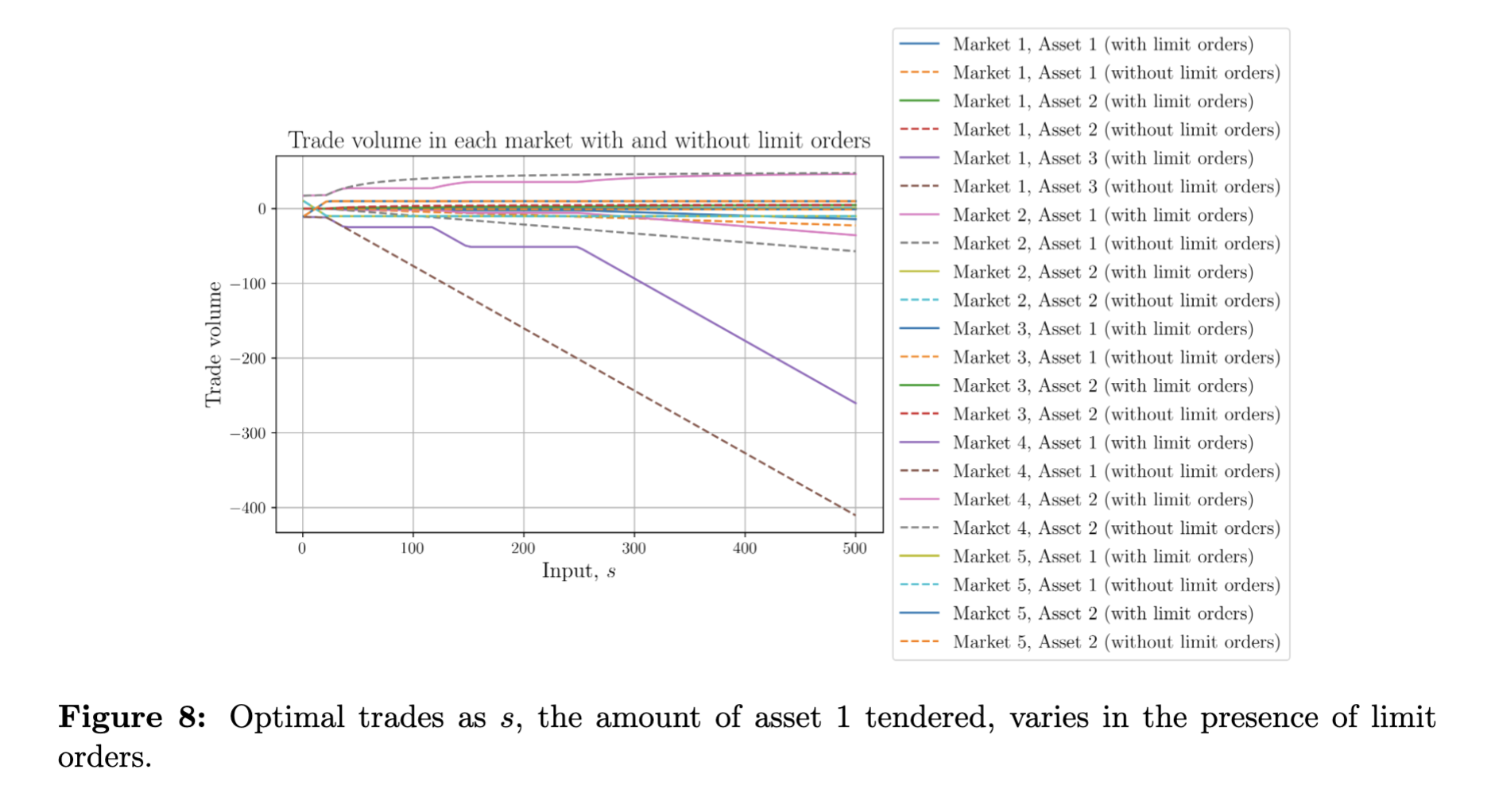
通过简单地引入额外变量 ${z_j}$ 代表每个限价单的交易，标准路由问题得到了扩展，每个限制在 $\tilde{T}_j$ 内。由于这些 $\tilde{T}_j$ 集合仍然是凸的，整个路由问题仍然是 凸的，并可以通过典型的凸求解器（如 cvxpy）进行求解。

• 债务猪网络及限价单（图 5-6）。这是一个经典的玩具示例，包含两条路径：一条是标准常数乘积 CFMM，另一条是单个限价单 $(p_0,V_0)$。通过一个简单的凸程序找到最优路径。结果与 $\tilde{G}$ 的分段形状相匹配。
• 一般多资产示例（图 7-8）。作者展示了如何处理五个 CFMM 和两个限价单。他们展示了用户的输出得到改善，以及在每个设定价格上限价单流动性被消耗时解决方案中的“拐点”。

最优清算：时间路由

在这里，用户有大量的 高风险 资产（例如 ETH）要出售为稳定资产（例如 USDC）。在 CFMM 上一次性完成这一操作会造成较大的价格影响。Uniswap v4 的 hooks 使得用户能够使用 TWAMM（时间加权自动市场制造商），用户可以发布一个单一的“虚拟”订单，该订单在多个小时间间隔内（或在区块时间内持续）部分执行。

然而，如果用户有 错误定价 或波动性的 信号，她可能希望采取更具策略性的方式——仅在 CFMM 的价格优于外部市场的价格时进行交易。这通过动态规划的马尔可夫决策过程（MDP）方法进行研究。

基于时间的 Hooks (TWAMM / 清算)

在典型的 CFMM 中，每笔交易都是无状态操作（池仅更新其储备）。Hook 可以在块之间持有附加状态——例如：

$$ \text{(状态)} = \Bigl{\text{本区块迄今已交易的代币数量},\; \text{自上一区块以来的时间}, \ldots\Bigr}. $$

这个状态可以反馈到有效的正向交换函数。例如，一个 hook 可能会表述：“区块中前 10k 的交易量费用为 0.3%，之后为 0.5%。”

这将导致收益 $\Delta'$ 的分段定义，依赖于在区块中迄今已交易的量。

• 如果这一逻辑仍然是分段线性或分段凹的，那么得到的可行 $\Delta$ 集仍然可以保持为凸的。但如果引入了离散跳跃或基于区块的限制，你可能会失去凸性。

• 作者显示，对于最优清算，你可以将用户的问题视为：

$$ \max\pi \; \mathbb{E}\Bigl[\textstyle \sum{t=1}^T U_t(\Deltat)\Bigr] \quad\text{subject to}\quad I{t+1} = I_t - \Delta_t,\;\; \Delta_t \in T(\text{状态}_t). $$

这变成了一个 马尔可夫决策过程 (MDP) 在 $(I_t,z_t)$ 中，其中 $z_t$ 是“错误定价”，而 $I_t$ 是“库存”。该 hook 有效地为用户提供了时间或状态的维度。解决方案通过动态规划给出：

$$ Vt(I,z)\;=\;\max{\Delta\in T(\dots)} \Bigl{\, R(I,z,\Delta) + \mathbb{E}[\,V_{t+1}(I-\Delta,z')\,] \Bigr}. $$

由于 $\Delta$ 通常是连续的而 $\text{状态}$ 可能很大或复杂，作者运行数值 DP 或近似方法。通常，这不再是单步的凸程序，而是一个 $\textit{序列}$ 问题。如果状态转移和即时奖励是足够规则的（在 $\Delta$ 中是凹的），你可以进行反向归纳或 Q学习 类型的方法。

建模错误定价过程

高风险资产的外部市场价格为 $p_t'$，池的链上价格为 $p_t$。定义

$$ z_t \;=\; \log!\bigl(\tfrac{p_t'}{p_t}\bigr), $$

即“对数错误定价”。存在一个 费用界限 区域 $(-\gamma-, \gamma+)$，在这个区间内，没有套利者会进行交易，因为收益太小而无法覆盖费用。如果 $zt$ 超出该区间，套利者便会进入并将其恢复为 $\pm \gamma\pm$。随后，如果用户也交易了 $\Delta_t$，链上的价格也会改变，导致错误定价发生“跳跃”。在区块与区块之间，$z_t$ 还遵循具漂移 $\mu$ 和波动性 $\sigma$ 的几何布朗运动。

TWAMM 与最优清算

• TWAMM 策略：用户将整个库存 $D$ 作为单一订单持续执行。价格滑点受到一定缓解，并且只支付一次Gas费。预期收益可以在未来路径的分布中进行计算。
• 最优清算策略：用户解一个离散时间的 MDP；在每个区块 $t$，状态为 $(I_t, z_t)$（剩余库存和当前错误定价），用户选择 $\Delta_t$ 进行出售。每次交易时有一个成本 $g$，还有每单位剩余库存的惩罚 $\xi$。由此产生的 贝尔曼方程 系统可以通过 值迭代 进行求解，得到：
  • 一个 价值函数 $V(I_t, z_t)$。
  • 一个 最优策略 $\Delta_t^*$，规定在每种状态下出售多少单位。

数值结果（图 9-12）

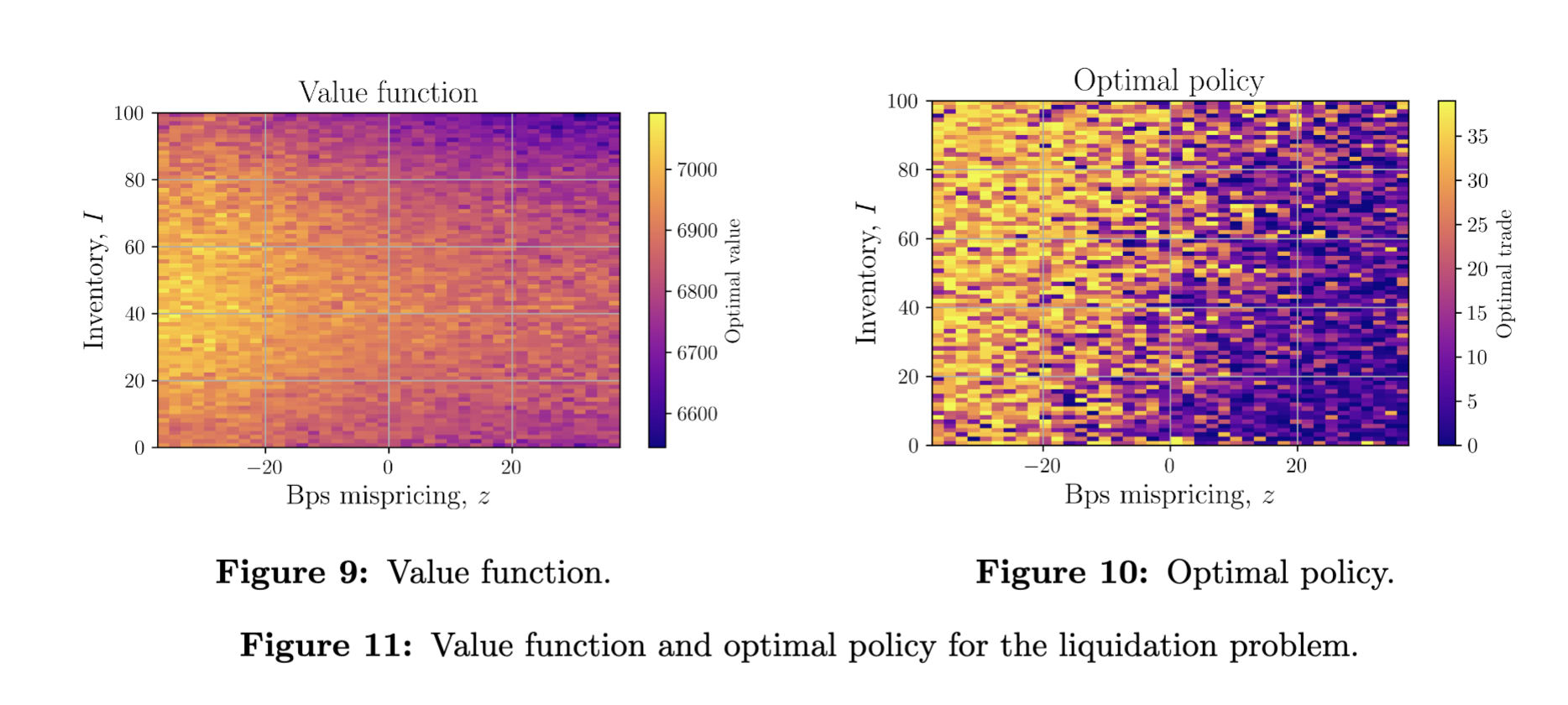
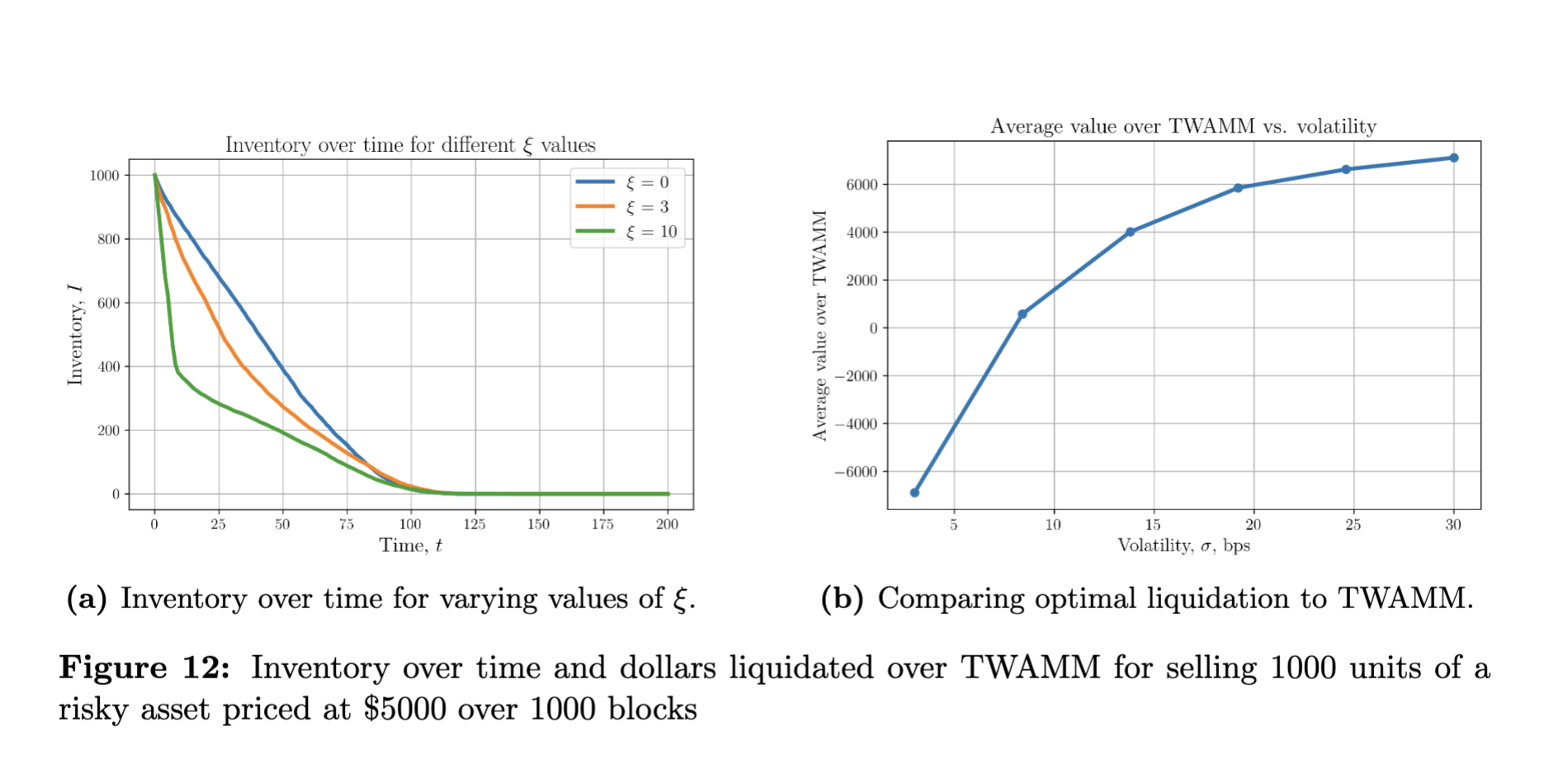
• 动态程序方法表明，如果波动性 $\sigma$ 较大，或者错误定价可能 有利，用户的表现好于简单的 TWAMM 策略（因为她在链上成本价更有利时会卖得更多）。
• 权衡包括支付多次Gas费和库存持有惩罚。
• 图 9（价值函数）和图 10（最优策略）表明，当错误定价为负时（即在卖出时 趋向于有利），用户会更积极地出售。
• 图 11-12 显示用户的库存在不同惩罚参数 $\xi$ 下的演变，并比较平均收益与 TWAMM 基准。

通过非可组合 Hooks 进行路由

第三种情况是 非可组合 hook：一个单独的流动性池（可能与外部市场制造商合作），无法与标准 CFMM 交易同步组合。用户看到 潜在更好的价格，但也面临“填充风险”—交易未能完全或部分填充的可能性，或最终实现输出的不确定性。

模型制定

用户希望将 $D$ 单位的资产 $A$ 交易为资产 $B$，决定多少 $\Delta$ 路由到可组合 CFMM 与多少 $D-\Delta$ 路由到不可组合 hook。

• 可组合 CFMM：一个标准常数乘积市场制造商，储备为 $(R, R')$。其正向交换函数为

$$ G_1(\Delta) \;=\; -\,\frac{R\,R'}{R + \Delta} \;+\; R'. $$

这是确定性的（忽略优先交易风险）。

• 非可组合 hook：

  • 它具有某种参数化的正向交换函数

    $$ G_2(\Delta) \;=\; 2\,\Delta \;-\; \frac{R_n'}{R_n}\,\Delta^{\,1+\alpha}\quad (\alpha \in[0,1]). $$

    更大的 $\alpha$ 使其更曲线化（更接近于“常数乘积–类型”的形状）；$\alpha=0$ 会使其线性（就像 hook 提供了固定价格）。

  • 其执行是 有风险的：用户可能并不实际以 概率 1 收到 $G_2(\Delta)$。

均值-方差优化

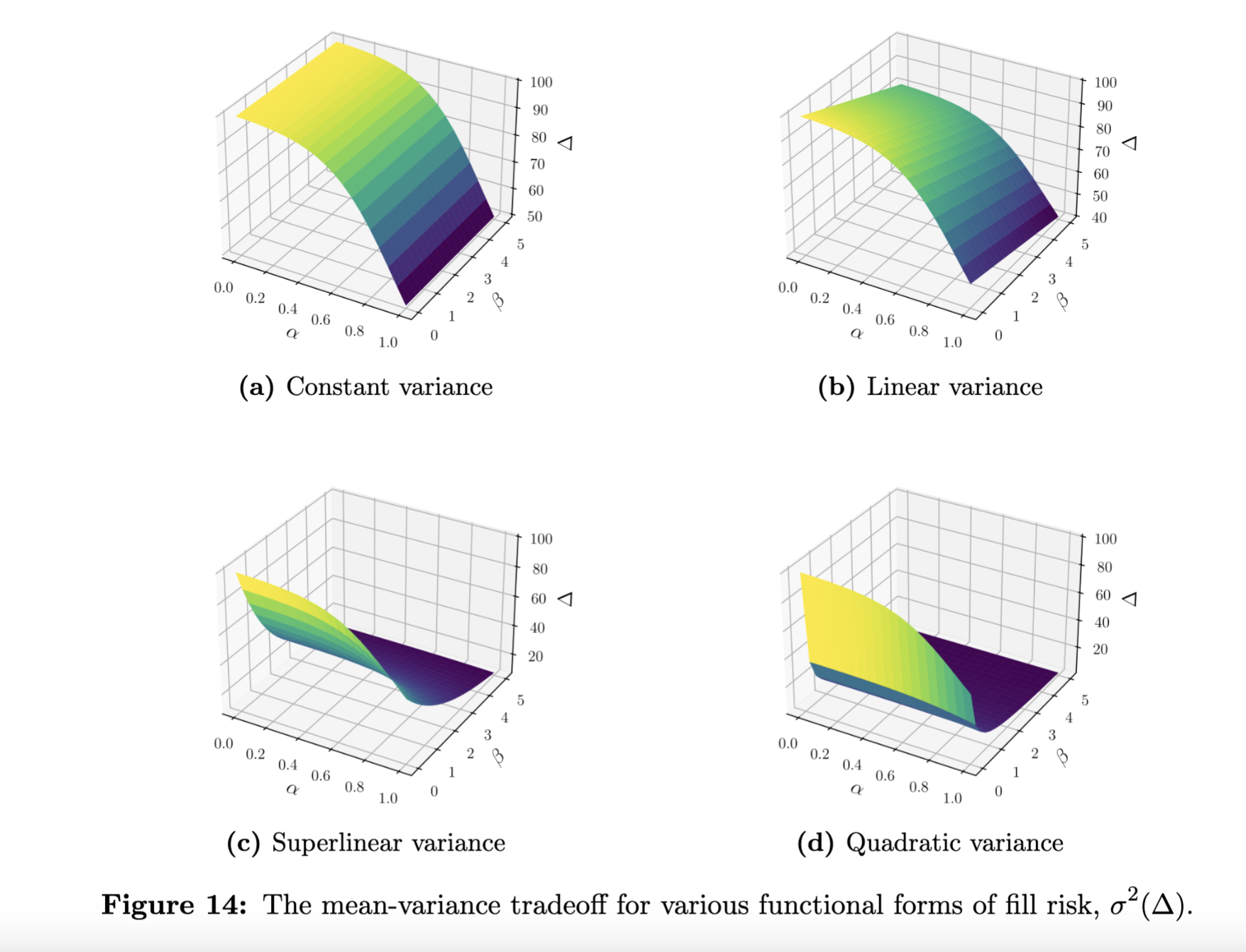
作者引入一个 方差 项 $\sigma^2(\Delta)$ 来建模填充风险。例如，$\sigma^2(\Delta) = \beta\,\Delta$ 或 $\beta\,\Delta^2$ 等，均捕获较大的交易面临更大的不确定性。然后定义目标

$$ \max_{\Delta}\quad G_1(D-\Delta)\;+\;G_2(\Delta)\;-\;\lambda\,\sigma^2(\Delta), $$

其中 $\lambda>0$ 是一个 风险厌恶 参数。只要 $G_1, G_2$ 是凹的并且 $\sigma^2(\Delta)$ 是凸的，就会得到一个凸程序。

• 结果： 当 $\alpha$ 较小时，用户会通过“风险” hook 进行更多交易，但随着 $\sigma^2(\Delta)$ 随着 $\Delta$ 的增长，路由器对在该 hook 中进行大型交易的倾向性减弱。

效率前沿

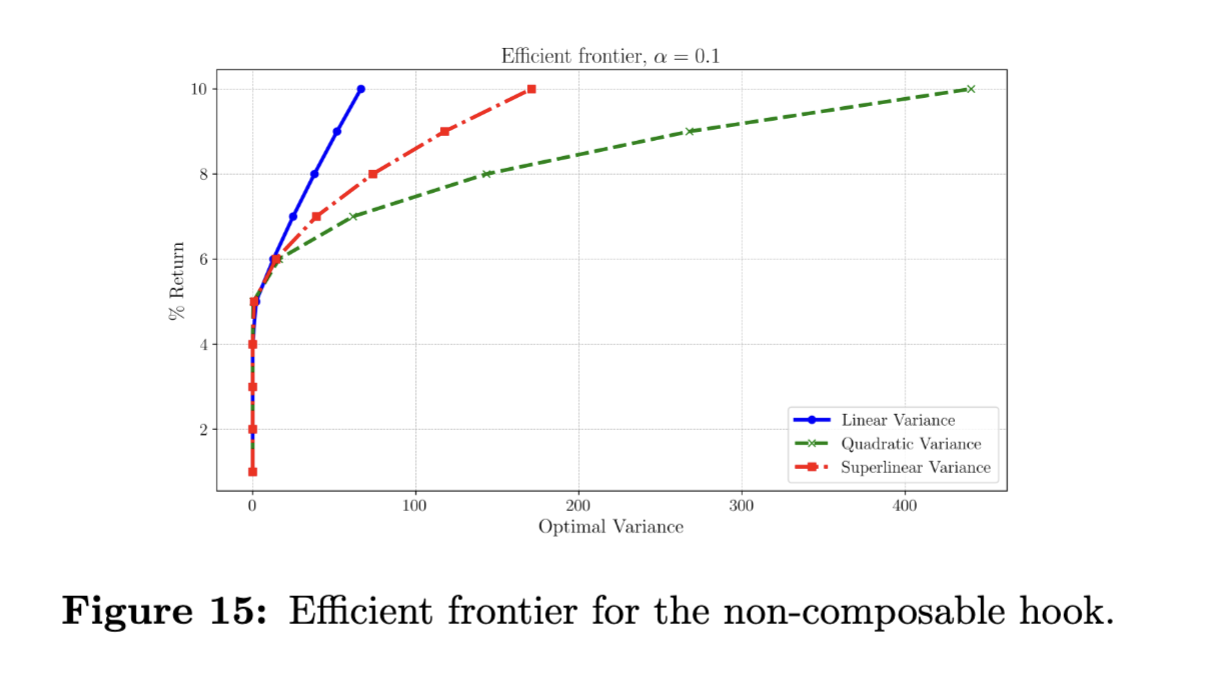
作者还计算了 效率前沿：达到指定目标输出 $\tau$ 所需的最低方差 $\sigma^2(\Delta)$：

$$ \begin{aligned} &\min_{\Delta} \quad \sigma^2(\Delta)\ &\text{subject to}\quad G_1(D-\Delta)+G_2(\Delta)\;\ge\;\tau,\quad 0 \;\le\;\Delta\;\le\;D. \end{aligned} $$

对于不同形状的 $\sigma^2(\Delta)$，可获得“可达风险与回报”的曲线。随着目标 $\tau$ 的增加，用户必须更多地分配到非可组合 hook（假设其价格更好），但风险却增加。这在论文中得到了图 14-15，说明对于超线性或二次方方差风险如何快速增长。

为什么有些 Hooks 保持凸性，有些则不然

• 保持凸性

  • 生成 $\textit{交易集 } T_i$ 形式的 hooks

  $$ T_i \;=\; \bigl{\, \Delta \mid f_j(\Delta) \le 0 \text{ for } j=1,\dots,k \bigr}, $$

  其中每个 $f_j$ 是凹的，使得路由问题成为标准的凸可行性。等价地，如果 hooks 导致的正向交换函数 $G(\Delta)$ 在 $\Delta$ 中是凹的，通常可以保持良好的凸结构。

• 打破凸性

  • 生成 $\textit{离散跃迁}$、具有不连续的分段定义或对块状态具有复杂依赖的 hooks 可能会导致可行 $\Delta$ 的非凸集合。
  • 示例：“前 10k 交易量支付 0.3% 的费用，然后下一 20k 交易量支付 0.5%。”在 10k 和 20k 之间的边界可能会使该区块中的 $(\Delta_1,\ldots,\Delta_m)$ 交易集合成为一个有效的“混合整数”或分段问题，这可能变得是 $\text{NP-hard}$。

结论

• 限价单可以被视为额外的凸约束或“在单一价格上的集中流动性”，并可轻松地纳入现有的 CFMM 路由框架中。
• 如果用户对外部错误定价有信号，则时间加权交易（TWAMM）可能是次优的。通过对错误定价的随机模型制定动态程序，用户可以做得更好，尽管这意味着更频繁地承担Gas费用。
• 非可组合 hooks 可以提供更好的价格，但增加填充风险。均值-方差方法捕获了这个权衡。用户可以计算多少交易发送到风险 hook 与保证的 CFMM。

参考文献

1. Chitra, Tarun et al., "在 Hooks 存在下的最优路由：三个案例研究，2025年。
2. Diamandis et al., 当通过常数函数市场制造商进行最优路由时的一种高效算法，2023年。
3. Guillermo Angeris 等人, Uniswap 市场分析，2021
4. Uniswap V4
5. Guillermo Angeris 等人, 尾巴是否摆动狗尾？曲率与市场制造，2022年。

• 原文链接： github.com/thogiti/thogi...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～