零基础学MPC 教程 - 每个人都可以学会
- zellic
- 发布于 2025-04-07 17:39
- 阅读 2544
本文介绍了多方计算(MPC)尤其是姚的加密电路协议的实现,涵盖了从理论基础到代码实现的各个方面,包括RSA、模糊传输、加密电路的生成与评估等。特别强调了如何在保持私人输入的隐私前提下进行安全计算,适合对MPC感兴趣的读者深入学习。
假设你和你的朋友都是百万富翁。你想找出谁更富有——但是不想向彼此透露各自的净资产。换句话说,你希望共同计算函数 $ a \geq b$,而不让任一方知道另一方的数值。这是一个经典的激励问题:百万富翁问题。
MPC为此类问题提供了解决方案。MPC,或多方计算,是指多个方如何在不透露其私密输入的情况下,对私人输入进行共享计算。实际上,MPC使我们能够安全地共同计算任何函数 $f(x_1, x_2, x_3, \cdots) $,其中输入的任意子集对于任一方都是私密的。(虽然有针对多个方的MPC协议,但我们在这篇文章中只讨论两个方的MPC。)
这听起来很酷,但可能吗?MPC实际上很容易实现。让我们从头开始走过一个基本的MPC实现。在几百行代码中,我们将构建执行Yao的加密电路协议↗所需的所有基本构件。

生成素数
为了进行MPC,我们需要非对称加密。最简单的非对称原语可能是RSA↗,而要进行RSA,我们需要生成一些素数。
我们可以通过猜测和检查来生成素数。然而,我们首先需要一种方法来快速检查一个数字是否为素数。有很多测试存在,但一个常见的测试是Rabin-Miller素性测试↗。这是一个基于初等数论的简单测试,且相当容易实现:
def rabin_miller(n, k=40):
if n == 2:
return True
if n % 2 == 0:
return False
r, s = 0, n - 1
while s % 2 == 0:
r += 1
s //= 2
for _ in range(k):
a = random.randrange(2, n - 1)
x = pow(a, s, n)
if x == 1 or x == n - 1:
continue
for _ in range(r - 1):
x = pow(x, 2, n)
if x == n - 1:
break
else:
return False
return True看看它是否有效。
>>> rabin_miller(101)
True
>>> rabin_miller(1234567891234567)
False
>>> rabin_miller(2**2203-1)
True不错。这是一个概率算法,其中参数 k 决定了你的确定性。这是因为我们选择的随机基数 a 的可能性存在微小的误报率。有趣的是,如果基数可以预先预测,那么可以伪造通过该测试但实际上是合成数的伪素数。不过我们在这里并不太关心,因为我们的素数候选是随机生成的。
在实践中,像 k=40 对于RSA大小的数字来说是可以的。它的运行时间是多对数时间,因此我们可以用它进行猜测和检查。在实践中,首次筛选出任何小素数会更快,然后再运行更昂贵的全测试。
def gen_prime(n=2048):
while True:
p = randbits(n)
p |= 1 # 我们只想要奇数
for p in SMALL_PRIMES:
if n % p == 0:
break
else:
if rabin_miller(p):
return pRSA
现在我们有了素数,可以进行RSA↗。RSA非常简单,所以我们只需进行。
def gen_rsa_params(n=2048):
p, q = gen_prime(n//2), gen_prime(n//2)
N = p * q
e = 65537
phi = (p-1)*(q-1)
d = pow(e, -1, phi)
return e,d,NPython 3.8及以上版本支持使用 pow(x, -1, N) 来进行模逆。在此之前,可以使用扩展欧几里得算法↗来进行。
像往常一样,加密为 pow(m,e,N),解密为 pow(c,d,N)。让我们测试一下:
>>> e,d,N = gen_rsa_params(32) # 小N用于示例目的
>>> (e, N) # 公钥
(65537, 2393534501)
>>> d # 私钥
2037798773
>>> m = 123456789 # 消息
>>> c = pow(m,e,N) # 加密
>>> c # 密文
1967143072
>>> pow(c,d,N) # 解密
123456789注意:这是教科书式RSA↗,这是不好的。在实践中,安全使用RSA并不容易,并且需要诸如填充↗、生成安全的随机数↗、避免侧信道攻击↗等内容。一般来说,你不应该自己设计加密,而是应该使用专家编写的库等等。(但这仅仅是出于学习目的,所以让我们继续。)
无知传输(Oblivious Transfer)
现在我们有了RSA,我们可以构建无知传输↗。无知传输是MPC的构建块。实际上,它对于MPC来说是完整的,这意味着你可以仅通过无知传输构建任何MPC。
在无知传输中,有两个方:_发送者_和接收者。发送者Alice有两个消息。她希望让接收者Bob选择接收这两个消息中的一个,而不透露另一个消息。然而,接收者也不想透露他选择了哪个消息。
这里有一个更直观的类比。假设你是发送者,而我是接收者。你把两个消息放进两个看起来相同的盒子里。然后,你转过身,我拿走其中一个盒子。当你转过身时,你无法知道我选择了哪个盒子,而我也不知道另一个盒子里有什么。
要用密码学实现这一点,我们将构建1–2无知传输。数字1和2表示接收者可以选择接收两个消息中的一个。首先,让我们考虑以下协议。该协议无法工作,我们将看到原因:
- Alice有消息 $m_0, m_1$。Bob希望接收 $m_b$,其中 b 是 0 或 1。
- Alice生成两个随机填充 $x_0, x_1$,将它们都给Bob。
- Bob也生成一个随机填充 k k k。
- Bob选择两个填充中的一个 $x_b$,然后用自己的填充将其盲化:$x_b + k$。这返回给Alice。
- Alice不能知道Bob选择了哪个 x,因为 k 是未知的。Alice减去她自己两个填充,得到$(x_b + k) - x_0$和$(x_b + k) - x_1$。这其中一个将等于 k,而另一个对Alice来说是没有意义的(例如,$x_1 + k - x_0$)。
- Alice取两个值,并用它们填充两个消息:$m_0 + x_b + k - x_0$和 $m_1 + x_b + k - x_1 $。其中一个将等于$ m_b + k$。这两个都发送给Bob。
- Bob从两个消息中去掉 k。一个将去掉变为$m_b$,Alice的其他消息对Bob来说是无用的,因为他无法在没有私钥的情况下预测其中填充的值, $(xb + k - x{b'})^d$。
在这个协议中,Bob成功接收了他的消息 $mb$,而不透露他选择了哪个。不过,有一个问题:Bob也可以算出另一个消息!由于Bob拥有x0和x1,他还可以恢复$m{b'} $。这打破了发送者只会透露所选消息的期望属性。
我们可以用非对称加密来修复这个问题。问题出在第5步,当Alice在发送之前对两个消息进行填充时。问题是Bob可以计算出两个消息的填充值。我们可以通过让Alice对她的值进行某种私钥运算(即解密)来解决这个问题。一个天真的尝试可能看起来像$m_0 + (x_b + k - x_0)^d$;然而,这样做不起作用。
问题在于:Bob现在如何去掉Alice的填充?没有私钥,他无法计算或预测其值。为了解决这个问题,我们将让Bob在第3步中加密他的盲化k。在这种情况下,当Alice在第5步中稍后解密填充时,这将抵消Bob的加密,留给一个填充值k,这个值是Bob知道的。对于另一个填充,它将解密为毫无意义的垃圾。现在,Bob将能够预测Alice的填充,而Alice用于另一个消息的填充仍是不可解码的。
这是完整的修订协议:
- Alice有消息$m_0,m_1$。Bob希望接收$m_b $,其中b是0或1。
- Alice生成两个随机填充$x_0,x_1$,将它们都给Bob。
- Bob也生成一个随机填充$ k $。他用Alice的RSA公钥加密它:$k^e$。
- Bob选择两个填充中一个$x_b$,然后用自己的加密填充盲化它:$x_b + k^e $。这返回给Alice。
- 即便拥有私钥,Alice也无法知道Bob选择哪个x,因为k可以是任何东西。Alice减去她的两个填充值得到$(x_b + k^e) - x_0$和$(x_b + k^e) - x_1$。其中一个将等于$ k^e $,另一个对Alice来说是毫无意义的(例如,$x_1 + k^e - x_0 $)。
- Alice 解密两个填充。一个会等于$k$,另一个则是毫无意义的。Alice取这两个值并用它们对两个消息进行填充:$m_0 + (x_b + k^e - x_0)^d$和$m_1 + (x_b + k^e - x_1)^d $。一个将等于$m_b + k$。这两个都发送给Bob。
- Bob从两个消息中去掉$k$。一个将去掉变为$m_b$。Alice的其他消息对Bob来说是无用的,因为他无法在没有私钥的情况下预测其填充的值$(xb + k^e - x{b'})^d$。
在这个新版修正协议中,Bob可以安全地接收他的消息,而Alice仅透露她的两个消息中的一个!
该协议是计算上安全的。它不是信息论安全的,意味着Bob可以使用猜测和检查来尝试猜测Alice的消息。然而,考虑到消息的大小足够,这不太可能发生。有信息理论安全的OT协议(例如,基于切割和选择的协议)。
现在,让我们在Python中实现它。由于这是一个互动协议,我们将使用协程模拟Alice和Bob之间的通信,使用yield来传递消息。
def oblivious_transfer_alice(m0, m1, e, d, N, nbits=2048):
x0, x1 = randbits(nbits), randbits(nbits)
v = yield (e, N, x0, x1) # 将参数发送给bob,等待他的回复
k0 = pow(v - x0, d, N)
k1 = pow(v - x1, d, N)
m0k = (m0 + k0) % N
m1k = (m1 + k1) % N
yield m0k, m1k # 回复两个填充消息
def oblivious_transfer_bob(b, nbits=2048):
assert b in (0, 1)
e, N, x0, x1 = yield # 从Alice接收参数
k = randbits(nbits)
v = ((x0, x1)[b] + pow(k, e, N)) % N
m0k, m1k = yield v # 将(x_b + k^e)发送给Alice,等待她回复
mb = ((m0k, m1k)[b] - k) % N
yield mb # 接收的消息!每个协程模拟了传输中的一个方。我们可以这样使用协程:
def oblivious_transfer(alice, bob):
e, N, x0, x1 = next(alice)
next(bob) # 运行Bob直到第一个yield语句
v = bob.send((e, N, x0, x1))
m0k, m1k = alice.send(v)
mb = bob.send((m0k, m1k))
return mb现在我们有了基本的MPC构建块,我们可以使用无知传输构建任何我们想要的MPC。这正是我们接下来要与加密电路一起做的事情。
加密电路
与其从上往下解释加密电路,不如从下往上构建它。总体想法是,我们使用1–2无知传输以MPC的方式评估各个逻辑门。然后“画出剩下的猫头鹰↗”(https://i.kym-cdn.com/photos/images/original/000/572/078/d6d.jpg)。做得好,现在你有了通用的MPC。
计算单个门
首先,让我们尝试对AND门进行MPC处理。我们的门涉及三根线:输入A和B以及输出线。假设Alice知道值A,Bob知道值B,而他们想共同计算输出Out。
我们将这样做。为所有三条线的每个布尔值0和1选择一个随机的k位数字,k是一个安全参数。我们称这些为标签。每条线有两个标签。
- $A_{ \color{blue}0} = 12214430034326763207138511821778...$
- $A_{ \color{red}1} = 15587367908968267934296553115483...$
- $B_{ \color{blue}0} = 66560761019031368742675262660503...$
- $B_{ \color{red}1} = \cdots$
- $Out_{ \color{blue}0} = \cdots$
- $Out_{ \color{red}1} = \cdots$
好的。现在让我们看一下真值表:
| A | B | Out |
|---|---|---|
| $\color{blue}0$ | $ \color{blue}0$ | $ \color{blue}0$ |
| $ \color{blue}0$ | $ \color{red}1$ | $ \color{blue}0$ |
| $ \color{red}1$ | $ \color{blue}0$ | $ \color{blue}0$ |
| $ \color{red}1$ | $ \color{red}1$ | $ \color{red}1$ |
对于每一行,取输出线值的标签。然后,使用对称密码,用从输入线值的标签派生的密钥对标签进行加密。
| Out |
|---|
| $Enc{A{ \color{blue}0},B{ \color{blue}0}}(Out{ \color{blue}0})$ |
| $Enc{A{ \color{blue}0},B{ \color{red}1}}(Out{ \color{blue}0})$ |
| $Enc{A{ \color{red}1},B{ \color{blue}0}}(Out{ \color{blue}0})$ |
| $Enc{A{ \color{red}1},B{ \color{red}1}}(Out{ \color{red}1)}$ |
此外,洗牌表格以便无法轻易判断每个逻辑输入值对应的是哪个值。
| Out |
|---|
| $Enc{A{ \color{blue}0},B{ \color{red}1}}(Out{ \color{blue}0})$ |
| $Enc{A{ \color{red}1},B{ \color{red}1}}(Out{ \color{red}1})$ |
| $Enc{A{ \color{red}1},B{ \color{blue}0}}(Out{ \color{blue}0})$ |
| $Enc{A{ \color{blue}0},B{ \color{blue}0}}(Out{ \color{blue}0})$ |
这就是所谓的加密表,用于AND门。
这就是MPC协议开始的地方。Alice将这个加密表和她的输入的标签(要么$A_0$,要么$ A_1$)给Bob。这不会泄露任何信息给Bob,因为他不知道标签对应的是什么。对Bob而言,它们只是随机数。Bob如何评估这个加密表?
假设目前Bob也神奇地知道他的输入的标签(不论是$B_0$还是 $B_1$)。有了这些,Bob可以遍历加密表中的四个条目,进行尝试解密↗,直到一个成功。然后他会得到一个输出标签,要么是$Out_0$,要么是$Out1$。举个具体的例子,如果Alice的值是0,而Bob的值是1,他就能解密正到Out0的标签$Enc{A_0,B_1}(Out_0)$。Bob将这个标签发送回Alice。
此时,Alice知道门的输出为0。记住她不知道Bob是0还是1——她只知道结果。Alice也与Bob分享这个结果。如果Bob不想盲目信任Alice的结果,他们可以整个协议再次运行,但交换角色,由Bob进行加密并发送表。
整体协议有效,除了一个问题。还记得我们假设Bob神奇地知道了他的输入标签?他应该如何向Alice询问而不透露他的输入?Alice可以发送两个标签,但这样Bob就可以利用这一点从加密表中提取信息。在我们的示例中,Bob现在可以解密两个表中的行。看到两个值相同,他可以推断出Alice的值一定是零,因为解密后的标签是同一值(如果Alice的值为1,输出将不同)。
为了解决这个问题,我们使用之前开发的无知传输!我们将让Bob通过1–2无知传输从Alice接收他的标签。Alice将让Bob选择$B_0$和$B_1$;Alice不知道Bob选择了哪一个,而Bob将只了解到他的输入值,而不必得知另一个。
最后一点,在这个例子中,Bob(输入为1)仍然能够推测Alice的输入为0,这是由于计算本身(AND函数)造成的,而不是协议的弱点。如果我们有一个包含更多输入位的电路,比如比较器,每个方会学到关于对方输入的信息相对较少。
单个门的实现
好的,让我们实际编码这个东西。
首先,我们需要一个对称加密原语。冒着违反文章标题的风险,我将只是导入AES↗。有更简单的原语(受欢迎的包括TEA↗和RC4↗),它们在这篇文章中同样适用,但是这些算法都较弱。(不管怎样,这不是本文的主要重点,所以我们继续。)
from Crypto.Cipher import AES
from Crypto.Util.Padding import pad, unpad
from Crypto.Util.number import long_to_bytes, bytes_to_long
def symmetric_enc(key, x):
cipher = AES.new(key, AES.MODE_CTR)
ciphertext = cipher.encrypt(pad(long_to_bytes(x), 16))
nonce = cipher.nonce
return ciphertext, nonce
def symmetric_dec(key, ciphertext, nonce):
cipher = AES.new(key, AES.MODE_CTR, nonce=nonce)
x = bytes_to_long(unpad(cipher.decrypt(ciphertext), 16))
return x让我们试试:
>>> key = b'This is my key__'
>>> ciphertext, nonce = symmetric_enc(key, 12345)
>>> ciphertext.hex(), nonce.hex()
('db6f1eef1b94bbc04016176f8dfbdd4765b7ab61355d087d8e869c15e77b8e29', '7ad8c3a7dff064e2')
>>> symmetric_dec(key, ciphertext, nonce)
12345好的!
为了将两个标签组合成一个密钥,我们可以使用一些哈希函数。我将使用Keccak↗。
from Crypto.Hash import SHA3_256
def combine_keys(keys, k=128):
h = SHA3_256.new()
for ki in keys:
h.update(long_to_bytes(ki))
return h.digest()现在,这里是实际的表格加密。首先,我们需要标记真值表,同时跟踪每个标签对应的线和逻辑值。
def label_table(logic_table, output_name, input_names, k=128):
labels = {}
# 为每个变量生成0和1的标签
for var in (output_name, *input_names):
labels[var] = [randbits(k), randbits(k)]
labeled_table = []
# 一些itertools的事,以支持任意数量的输入线
# 输入线的数量=逻辑表的维数
for inp_values in itertools.product((0,1), repeat=len(input_names)):
output_value = functools.reduce(operator.getitem, inp_values, logic_table)
output_label = labels[output_name][output_value]
input_labels = [labels[input_names[i]][v] for i, v in enumerate(inp_values)]
labeled_table.append((output_label, input_labels))
return labeled_table, labels让我们试试。我们将$k=5$,以便标签较小,以作说明。
>>> labeled_table, labels = label_table([[0, 0], [0, 1]], "out", ["A", "B"], k=5)
>>> labels
{'out': [30, 27], 'A': [28, 19], 'B': [17, 30]}
>>> labeled_table
[(30, [28, 17]), # 0 = 0 & 0
(30, [28, 30]), # 0 = 0 & 1
(30, [19, 17]), # 0 = 1 & 0
(27, [19, 30])] # 1 = 1 & 1好的。现在,让我们加密这个表:
def garble_table(labeled_table, k=128):
result = []
for row in labeled_table:
output_label, input_labels = row
key = combine_keys(input_labels)
c, nonce = symmetric_enc(key, output_label)
result.append((c, nonce))
Crypto.Random.random.shuffle(result)
return result让我们测试一下:
>>> garble_table(labeled_table)
[(b'\x02\xd6H\x01\xb2\xc9\xbe*"\x842\xb77\xf5\x81\xd2\xd2\x00\xbb\xb9\xcc\xce5\xe5\x89\x94\xc7"w\x03\x14>', b'\xdc\x0bWT\x8cM\xda\x01'),
(b'\x9f\xd7\xe71\x922V\x92s\x90Z\x81tY\x0f5\xa2K/\xb7\x10\xf5\xbec\xd0\xff&\x05\x82\xc2\x80 ', b'\x95[\xf6Q&kZE'),
(b'\xe7A\x8e\xf2#+\xcd\xc9\xa2\xe8\xb4p\xbdd\x93_ \\xf7U\xdc\x01u\xb6,JW\x18\xa2\xb5~\xe6\xd6', b'\xc1\xde\xca\xc5\xe90tu'),
(b'\xfa\xdc\x9d\xe5&\x81\x03q\xf4\x15\x1c%\xc2t\xb0\xbf\x0b0Vk\xbdNm\xe8CT\xb3\x01\xd7\x82\xe7\x12', b'J,q)B\x88\xe9r')]
这个混淆表看起来像一个加密的二进制块,正如预期的那样。要评估混淆表:
def eval_garbled_table(garbled_table, inputs):
for row in garbled_table:
ciphertext, nonce = row
try:
key = combine_keys(inputs)
output_label = symmetric_dec(key, ciphertext, nonce)
except ValueError: # 解密失败,填充不正确
continue
return output_label
>>> a, b = 1, 1
>>> eval_garbled_table(garbled_table, [labels['A'][a], labels['B'][b]])
27
>>> labels['out'][1] # 验证这是否与 out=1 的标签匹配
27
它工作了!接下来我们也在 NOT 门上试试。通过 AND 和 NOT,我们在功能上是完整的。
>>> labeled_table, labels = label_table([1, 0], "out", "x", k=5)
>>> labels
{'out': [23, 25], 'x': [31, 24]}
>>> labeled_table
[(25, [31]), (23, [24])]
>>> garbled_table = garble_table(labeled_table)
>>> eval_garbled_table(garbled_table, [labels['x'][0]])
25
>>> labels['out'][1]
25
很好!但是,我们的对称加密有一个大问题。每隔一段时间,解密在我们的混淆表中的错误行意外地成功。由于偶然性,解密有有效填充,而我们的混淆表评估器产生了错误的结果。我们如何防止这个问题呢?
防止试验解密中的假阳性
在某种意义上,我们的填充像是一个校验和,通过使随机解密成功的可能性不大。这里有一个例子:\
>>> from Crypto.Util.Padding import pad, unpad
>>> pad(b'test', 16)
b'test\x0c\x0c\x0c\x0c\x0c\x0c\x0c\x0c\x0c\x0c\x0c\x0c'
>>> unpad(b'test\x0c\x0c\x0c\x0c\x0c\x0c\x0c\x0c\x0c\x0c\x0c\x0c', 16)
b'test' # <-- 成功的去填充
>>> unpad(b'test\x0c\x0c\x0c\x0c\x0c\x0c\x0c\x0c\x0c\x0c\x0c\x0d', 16)
只有一个字节改变! ^
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "python3.10/site-packages/Crypto/Util/Padding.py", line 95, in unpad
raise ValueError("PKCS#7 padding is incorrect.")
ValueError: PKCS#7 padding is incorrect.
这类似于一种错误检测。也许我们可以通过使用校验和来加强这一点。我们可以使用像弗莱彻校验和或 CRC-32 这样的简单校验和。不幸的是,虽然这能降低错误率,但我们仍然遇到校验和_意外_有效的情况。
那么,对于 SHA-2 这样的加密哈希函数呢?这将保证消息在意外有效的情况下不会出现。因此我们只需在末尾添加一个哈希,对吗?也许,但一般来说,这种方式非常容易↗出错。我们真正想要的是 认证加密模式↗。认证加密不仅保护明文的机密性,还保护真实性(即,完整性)。
我们可以构建一个认证加密,假设使用 HMAC↗ 和我们的分组密码配对,但更容易使用 GCM↗。GCM 性能优越,仅使用 AES 即可实现认证加密,而无需引入其他加密原语。将我们的代码修改为使用 GCM 代替 CTR 模式是简单的。这里是更新后的代码:
def symmetric_enc(key, x):
cipher = AES.new(key, AES.MODE_GCM)
ciphertext, tag = cipher.encrypt_and_digest(pad(long_to_bytes(x), 16))
nonce = cipher.nonce
return ciphertext, tag, nonce
def symmetric_dec(key, ciphertext, tag, nonce):
cipher = AES.new(key, AES.MODE_GCM, nonce=nonce)
x = bytes_to_long(unpad(cipher.decrypt_and_verify(ciphertext, tag), 16))
return x
现在我们的代码不再依赖填充来检测无效解密(填充本身并未设计用于此!)。相反,我们依赖于 GCM,这是专门为解决此问题而设计的。请注意,现在我们不仅要存储密文和随机数,还需要存储一个标签。你可以把这个标签看作一个像 MAC 一样的完整性检查。
计算两个门
现在我们可以混淆并评估一个门。那两个串联的门呢?
基本上与之前的原理相同。我们为所有线路生成逻辑值 0 和 1 的标签:输入线 A、B 和 C;中间线 X;以及输出线 Y。然后我们混淆两个真值表,每个门一个。

为了评估电路,我们按顺序评估门,从输入开始,向前推进。因此,我们首先会评估门 1 的混淆表,以获得线路 X 的解密标签;然后,我们可以评估门 2 的混淆表,以获得线路 Y 的解密标签。

支持 N 门
现在我们有了基本情况,也有了归纳情况。我们基本上可以做任何任意电路。
我们将电路表示为有向图,其中边是线路,节点是门。这通常被称为 netlist↗。
电路的混淆版本是Alice传输给Bob的内容。这也是有向图,具有与原始电路相同的连通性,但节点是混淆表而不是门。网络(及其门)可以有任意数量的输入和输出线路。一些输入是Alice私人拥有的,一些是Bob私人拥有的。与 1 门示例一样,Alice公开将她的输入线标签提供给Bob。对于Bob的输入线,他通过盲转移从Alice那里接收它们。
为了评估电路,Bob从输入线开始,按 拓扑顺序↗ 迭代访问门。在拓扑顺序中,当一个节点被访问时,其所有前驱都已被访问。在我们的情况下,这意味着在我们评估一个混淆表时,所有输入线的标签都是可用的。
你可以在 这里↗ 找到这个算法的代码实现。
逻辑综合
这很好,但我们难道真的期望自己手动构建所有我们希望使用门级逻辑的 MPC 计算吗?也许手动编写像 N 位比较器或全加器这样的东西很简单,但复杂计算呢?如果我们想要 MPC 的以下内容—— Sign(message, key=Hash(Alice key, Bob key))(例如,为了创建一个 2-of-2 多签名),我们显然不必从门开始重新实现非对称加密和哈希函数,对吗?幸运的是,这是一个已经解决的问题。我们可以用 HDL↗(如 Verilog)编写高级代码,并将其综合成门级逻辑。
如果你不熟悉硬件设计,HDL 是一种编程语言,但用于电路设计。对于这个类比要小心,因为一些熟悉的编程语言概念不能直接转换到电路中。例如,我们在传统意义上并没有“循环”;我们可以通过有限次数展开来假装有一个循环。而且,与编程语言中的变量不同的是,线路不应该被多次赋值(即,被多个事物驱动)。从某种意义上说,一切都是 全局值编号↗,就像 SSA 形式↗。如果你做过符号执行或者使用过 SMT 求解器,这些差异你会很熟悉。
对于实际的综合,有一些流行的开源工具,如 Yosys↗。Yosys 还处理 技术映射↗。技术映射的主要思想是我们告知综合工具我们可以使用的门 / IP 块 / 单元,综合工具将尽力生成一个良好的设计。如果你以前写过 LLVM 后端,我喜欢把这看作是 LLVM 的 模式匹配↗ 和降级。
作为我们第一个非平凡的 MPC 示例,假设Alice和Bob有两个 32 位数字 x 和 y,并想要查看它们是否是彼此的乘法逆。我们可以轻松在 Verilog 中编写此逻辑:
// circuit.v
module mycircuit(x, y, out);
input wire [31:0] x;
input wire [31:0] y;
output wire out = (x * y) == 1;
endmodule
我们可以使用以下 Yosys 脚本将其综合为门:
## 读取设计
read_verilog circuit.v
## 主要逻辑综合步骤
synth
## 技术映射步骤。告知 yosys 我们的平台支持的门
## 我们仅实现了 AND 和 NOT 门,因此告知 abc 这一点
abc -g AND # 'NOT' 总是自动添加
## 调整设计,以便只使用 1 位线路
splitnets -ports -format _
## 杂项清理
clean_zerowidth
clean -purge
## 保存降级设计
write_verilog -simple-lhs -noattr out.v
生成的门级设计如下所示:
 \
\
为了好玩,如果我们用 Graphviz 可视化它,这就是它的样子。32 位设计太大了,无法显示,所以这里是 4 位版本:
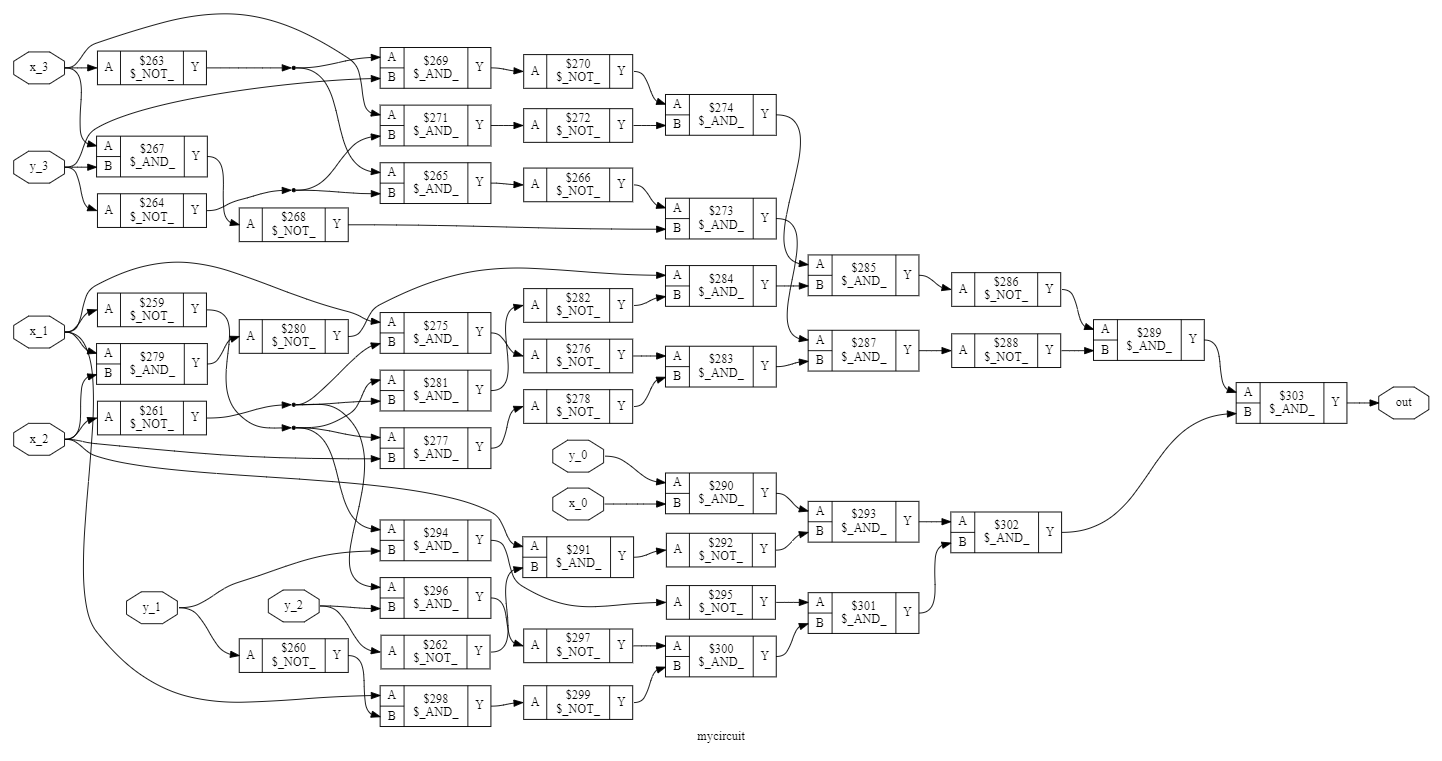
当然,我们很高兴让 Yosys 为我们生成这个,而不是手动编码。这只是一个简单的乘法器。想象一下,对于更复杂的计算,设计会有多复杂!
综合所有内容
此时,我们准备好实际进行我们的 MPC。再次在示例中,Alice和Bob希望确认他们的两个 32 位数字,XXX 和 YYY,是彼此的乘法逆。Alice的输入 XXX 是 1185372425,而Bob的输入 YYY 是 1337。电路将是 out = (x * y) == 1。让我们试试。
 \
\
我们现在可以看到所有步骤的实际操作。首先,它创建电路中的所有门。然后,它为每个线路分配标签。Bob使用盲转移接收他的输入标签,然后以拓扑顺序评估所有门。最后,他将输入标签返还给Alice,Alice发布结果:out=1。好极了!
现在让我们研究一些使我们的实现更高效的方法。
优化 1:避免试验解密
对于每个门,我们必须在找到混淆表中的正确条目之前进行最多四次试验解密,或者在平均情况下 2.5 次解密。这效率低下,我们可以做得更好。
我们可以通过在每一行中编码信息,以表示它对应于哪些输入密钥,从而避免试验解密。这种方法在 这篇论文↗ 的第 5.1 节中用复杂的数学方程进行了描述,但我将在这里用普通的英语概要说明。
首先,回想一下每个密文是用从两个输入标签派生的联合密钥进行加密的,每根线有一个标签。对于每根输入线,有两个标签:一个用于逻辑 0,另一个用于逻辑 1。未经损失的可一般性,我们可以生成两个标签,使其最低有效位 (LSB) 总是不同。这并不会泄露有关实际逻辑值的信息,因为逻辑 0 的标签可能具有 LSB 1 或 0;毕竟标签是随机的。然后,对于每个表条目,我们将两个标签的 LSB 附加到密文:
| 输出 | |
|---|---|
| $Enc{A{ \color{blue}0},B{ \color{red}1}}(Out{ \color{blue}0}) | LSB(A_0) | LSB(B_1)$ | \ |
| $Enc{A{ \color{red}}1,B{ \color{red}1}}(Out{ \color{red}1}) | LSB(A_1) | LSB(B_1)$ | \ |
| $Enc{A{ \color{red}}1,B{ \color{blue}0}}(Out{ \color{blue}0}) | LSB(A_1) | LSB(B_0)$ | \ |
| $Enc{A{ \color{blue}0},B{ \color{blue}0}}(Out{ \color{blue}0}) | LSB(A_0) | LSB(B_0)$ | \ |
然后,我们可以寻找与输入标签匹配的 LSB。
更好的是,我们可以按两个 LSB 对表进行排序(这在安全上是可行的,因为 LSB 是随机的),以便以 O(1)O(1)O(1) 索引。到那时,由于信息通过行的排列隐式编码,我们也可以移除附加的 LSB。通过这个优化,我们可以选择不使用认证加密,因为我们应该总是拥有正确的密钥对应于相应的密文。
优化 2:支持更多门\
我们的 MPC 实现可以正常工作,但综合电路非常庞大。为了使实现更高效,我们将增加对超出 AND 和 NOT 的一些其他门的支持。这里是我们目前支持的门:
def truth_table(gate):
if gate == 'and':
return [[0, 0], [0, 1]]
elif gate == 'not':
return [1, 0]
elif gate == 'const_0':
return 0
elif gate == 'const_1':
return 1
else:
raise ValueError('unsupported gate', gate)
Yosys 输出的设计非常庞大,因为它必须仅从 AND 和 NOT 门综合一切。但就我们的 MPC 而言,我们的混淆电路非常庞大且评估速度慢——电路的_深度_非常大。如果我们有更多的门类型可供使用,Yosys 将能够综合出一个更小的电路。
从技术上讲,我们真正需要的是 NAND。在现实生活中,更复杂的单元与单元尺寸之间存在一些实际权衡。如果单元较简单,则可以在给定的平面或晶圆上放置更多。相同的原理也适用于我们的 MPC。对于我们来说,如果使用更复杂的真值表,我们可以综合出具有更少门(深度)的小电路。这会影响评估复杂性。然而,门的输入数量(宽度)会影响混淆表中的条目数量,从而影响我们协议的通信复杂性。
更抽象地说,我们正在研究电路宽度和深度之间的权衡。我们可以将整个计算编码到一个巨大的真值表中,但表大小与宽度成指数关系。通过使用多个较小的门,我们权衡出一些宽度——更深但宽度较小。这就是为什么混淆电路相对单纯的盲转移如此重要的原因。
无论如何,我们已经在使用 AND 门,其宽度为 2(= 四个真值表条目)和 NOT 门,其宽度为 1(= 两个真值表条目)。当 Yosys 综合 NOT(AND(...)) 时,这实际上是六个表条目。一个无窥优化是也增加 NAND 门,它常量折叠了这个外部的 NOT 门。但我们可以进一步支持常见的双输入门类型。让我们通过将这些真值表硬编码来增加对 AND、NAND、OR、NOR、XOR、XNOR、ANDNOT 和 ORNOT 一组简单门的支持。
# [...]
elif gate == 'nand':
return [[1, 1], [1, 0]]
elif gate == 'xor':
return [[0, 1], [1, 0]]
elif gate == 'nor':
return [[1, 0], [0, 0]]
# [[... 你明白了]]
我们更新 Yosys 脚本中的 abc 调用:
## 现在我们有了更多的门!请使用它们
## 'gates' 是 AND,NAND,OR,NOR,XOR,XNOR,ANDNOT,ORNOT 的简写
abc -g gates
现在,如果我们查看综合的设计,它显著更小了。之前的设计有超过 8000 个内部线路,而新的设计只有 3000 个。不仅如此,如果我们计算混淆电路中条目的总数,它也更少了。新的设计总共有 12056 个条目,而旧设计有 24842 个。增加对这些额外门的支持将条目数量减少了 50%!
最后,供娱乐,这里可视化的 4 位设计——使用新的门类型。

查找表 Lookup Tables
然而我们可以做得更好。Yosys 中的技术映射步骤支持直接合成到查找表 (LUT) 中。除了考虑门,这正是我们真正想要的,因为我们的混淆电路实质上只是一个真值表网络。
我们可以指定我们希望 LUT 有多大(即,输入数量)。这里有一个宽度-深度权衡,因为更大的 LUT 导致电路深度减少,但表条目增多。nnn 输入查找表中的条目数量为 2n2^n2n,因此我们预计最佳 nnn 会很小。与此同时,ABC 主要优化电路深度,而牺牲面积。
| $n$ | # LUT2 | # LUT3 | # LUT4 | # LUT5 | # LUT6 | # LUT 总计 | 总 LUT 条目 | 电路深度 |
|---|---|---|---|---|---|---|---|---|
| 2 | 1607 | 2098 | 6428 | 44 | ||||
| 3 | 709 | 942 | 1638 | 10372 | 26 | |||
| 4 | 653 | 920 | 46 | 1376 | 10708 | 19 | ||
| 5 | 330 | 360 | 106 | 489 | 1285 | 21544 | 16 | |
| 6 | 548 | 256 | 66 | 80 | 471 | 950 | 36116 | 12 |
不意外的是,我们确实感受到了更大 LUT 所带来的指数成本,因此我们让我们坚持更小的 LUT。要进行 LUT 合成,我们可以像这样修改 Yosys 脚本中的 abc 调用:\
abc -lut 4综合后的代码看起来像这样:
// [...]
assign _0735_ = 16'h7888 >> { x_14, y_1, x_15, y_0 }; // 4-way LUT
assign _0736_ = 8'h78 >> { _0737_, x_10, y_5 }; // 3-way LUT
assign _0737_ = 16'h7888 >> { x_11, y_4, x_12, y_3 };
assign _0738_ = 16'hb24d >> { _0739_, _0684_, _0677_, _0676_ };
// [...]
进一步优化
在我们的混淆电路实现上,还有许多方法可以进一步改进。作为进一步阅读,有以下内容:FreeXOR↗,具有零成本的 XOR 门;半门↗,每个门使用两个 AES 而不是四个;以及 切分与调整↗,每个门使用 1.5 AES 块长度。我们不打算详细介绍这些论文,但如果你对如何使混淆电路在现实用例中更高效感兴趣,我们推荐你了解一下这些内容。
讨论
在结束之前,让我们讨论一些值得提出的事项。
组合逻辑
在此时,请注意,我们只有组合逻辑↗,没有时序↗。这意味着我们没有触发器或翻转器。由于缺乏时序逻辑,我们没有寄存器,因此我们无法构建任何有状态的内容。CPU 实际上是状态机。如果我们想要构建一个通用的 MPC “CPU”,我们需要调整我们的加密原语。我们可以通过展开循环并每个周期复制一次 CPU 设计来模拟 CPU 周期,但这非常低效。在电路中减少重复的一个优化是出口并重新输入任何状态作为线路,并多次运行混淆电路(即每个周期进行一次求值)。
半诚实与恶意模型
我们的 MPC 实现是在假设参与者是 半诚实 ↗。这意味着参与者会尽一切可能窃取他人私密信息,但他们不会偏离协议。这意味着,例如,他们确实不会提供虚假的或恶意的输入或响应给协议。
更现实的模型是_恶意_模型。在这个模型中,敌方操纵并控制计算中多个参与者,可以遵循任何多项式时间策略试图攻击协议。我们不会在这篇博客文章中涉及这一点,但混淆电路可以扩展以在两种状态下工作。例如,切分与选择技术↗让混淆者承诺一组电路,评估者首先打开子集以检查它们是否计算正确的函数,然后将未打开的电路用于协议的其余部分。\
进一步阅读
请查看以下资源:
结论
在这篇文章中,我们构建了一个可用的 MPC 实现,以 Yao 的混淆电路协议的形式。我们从零开始构建了所有必要的原语。首先,我们构建了素数生成和 RSA,然后从那个非对称原语构建了 1-2 盲转移。利用盲转移作为 MPC 构建块,我们然后开发了混淆电路。我们解释了混淆和评估单个真值表的工作原理,然后扩展成完整电路。最后,我们回顾了如何使用逻辑合成和硬件设计工具来进行我们的 MPC。
你可以在 GitHub↗ 找到这个项目的完整实现代码。我们鼓励你去看看!
感谢
我想感谢 Catherine (whitequark)↗ 在 Yosys 和硬件与逻辑合成部分的有益反馈和建议。
我还要感谢来自 Zellic 加密团队的 Avi Weinstock 和 Mohit Sharma,感谢他们对混淆电路细节的有用反馈。
关于我们
Zellic 专注于保护新兴技术。我们的安全研究人员在从财富 500 强到 DeFi 巨头的最有价值目标中发现了漏洞。
开发人员、创始人和投资者信任我们的安全评估,以快速、自信且没有关键漏洞地上市。凭借我们在现实世界攻击性安全研究中的背景,我们能够发现他人遗漏的内容。
联系我们↗,享受比其他审计更优质的审计。真正的审计,而不是橡皮图章。
- 原文链接: zellic.io/blog/mpc-from-...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 以太坊协议研究学习小组 - 2026 启动 146 浏览
- 神奇的 Zig、C 和 OpenSSL 170 浏览
- Shamir份额的魔力:BLS门限签名 418 浏览
- zkMesh:2026年1月回顾 427 浏览
- FRI (and friends) 使用 Lean4 形式化验证 FRI(及相关内容) 408 浏览
- ZK 编年史:电路(第二部分) 410 浏览
- 我对 2026年隐私的论点 1003 浏览
- Zig语言实现的社会主义百万富翁问题 584 浏览
- 有限域之美与力量 (以及 Zig) 503 浏览
- 扳手攻击:发生与预防 533 浏览
- zkEVM 安全性概览 608 浏览
- 基于哈希函数的签名(三):多次签名 682 浏览


