理解Schnorr和Musig

理解 Schnorr 和 Musig

内容

1. Schnorr 签名
   • 椭圆曲线中的加密方法
   • Schnorr 签名的实现原理
   • 签署消息
   • 验证签名
   • 为什么非对称随机数是必要的
2. 基于 Schnorr 签名的 Musig 实现
   • 聚合公钥
   • 密钥抵消攻击
   • 聚合随机数
   • 聚合签名
   • Musig 三轮通信的完整过程

Schnorr 签名

椭圆曲线中的加密方法

​ 在学习 Schnorr 签名之前，首先需要基于椭圆曲线创建公钥和私钥对。椭圆曲线上的点可以执行一些代数运算，涉及标量和点的概念。标量是正整数，用小写字母表示（例如，k），曲线上的点用大写字母表示（如 A）或一对坐标表示（例如，（x，y））。标量和点支持下图所示的运算。

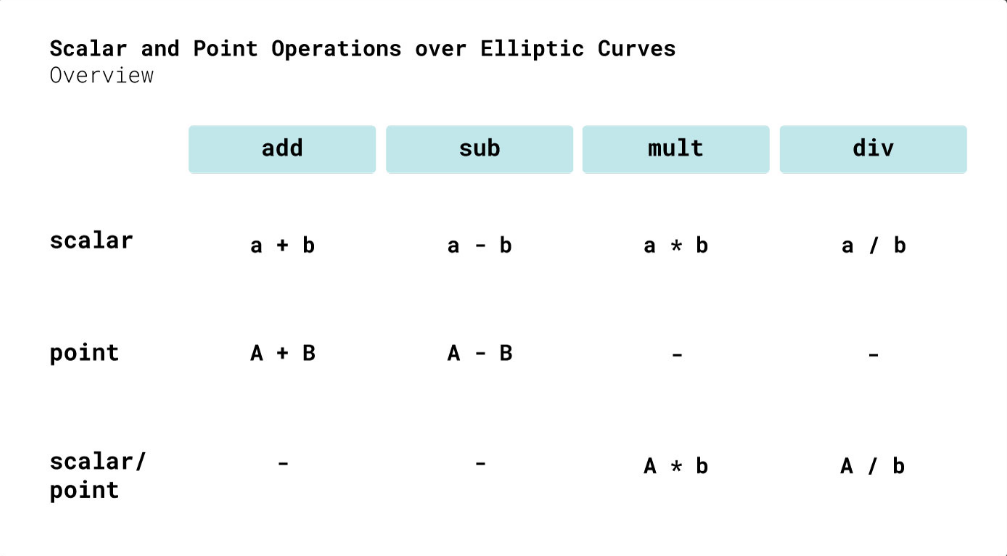
​ 从图中可以看出，标量与点之间可以进行乘法和除法运算，但点与点之间的乘除法是不成立的。进一步说明，如果有一个点 GMague G 将自身加了多次得到 R = G + G + G = 3 * G，则 G 和 R 可以被视为加密前后的点，而 3 是一个标量（实际上这是一个非常大的数）。如果已知 3 和 G，那么 R = 3 * G 可以很容易地计算出来，但如果只知道加密后的点 R 和加密前的点 G，我无法通过R / G得到一个等于 3 的标量 k，因为点无法满足该运算。上述情况与生成公钥和私钥对的过程相似。标量 k 被认为是私钥，而加密点的纵坐标被认为是公钥。要逆向破解私钥 k 的唯一可行方式是猜测标量 k 的值，即 k * G = R，然后枚举 k 得到答案。在比特币中，公钥和私钥对是通过 SECP256K1 曲线生成并签署的。标量的值是一个在 0 到 $2^{256}$ 之间的整数，这等于整个宇宙中原子的数量，因此可能性无穷，从而确保生成的公钥和私钥对的安全性。

​ 椭圆曲线是一组由 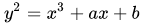定义并满足 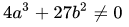的点集，其中不同的参数值对应于不同的椭圆曲线。对于每个 X 轴的值，对应于 Y 轴的 y 和 -y 的值，这两个纵坐标的值中只有一个满足 SECP256K1_FIELD_SIZE 模数的二次剩余，可以通过 jacobi_symbol 确定，该有效的 y 值就是公钥。因此，从私钥 d 可以无歧义地生成一个点 P = k* G，并可以得到其有效的 y 轴值作为公钥。

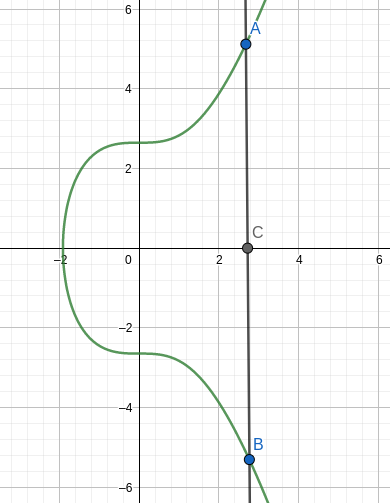
​ 上述不对称性是讨论 Schnorr 签名的前提。

Schnorr 签名的实现原理

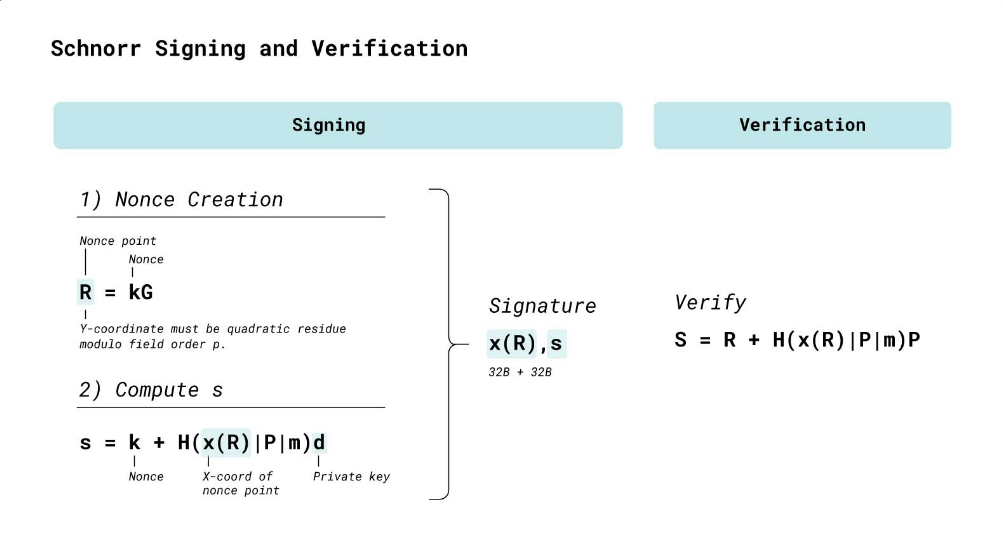
要使用 Schnorr 签署消息 m，首先需要定义几个变量：

• G：椭圆曲线。
• m：要签名的数据，通常是 32 字节的哈希。
• d, P：用户持有的私钥 d 和公钥 P，其中 P = d * G。
• H()：哈希函数。
• 其他：H(m | R | P) 可以理解为将 m、R、P 字段拼接在一起然后进行哈希处理。
• 另一个：X(R) 表示点 R 的横坐标值。

签署消息

以下方法用于创建 Schnorr 签名：

• 创建一个随机数 k，并从 k 创建一个随机点 R，其中 R = k* G。
• 计算标量 s = k + H(x(R) | P | m) * d，其中 P 为公钥，d 为私钥，m 为消息。
• 最终的 Schnorr 签名为 S = (x(R), s)，是一个值对，由 32 字节的 x(R) 和 32 字节的 s 组成，最终长度为 64 位。

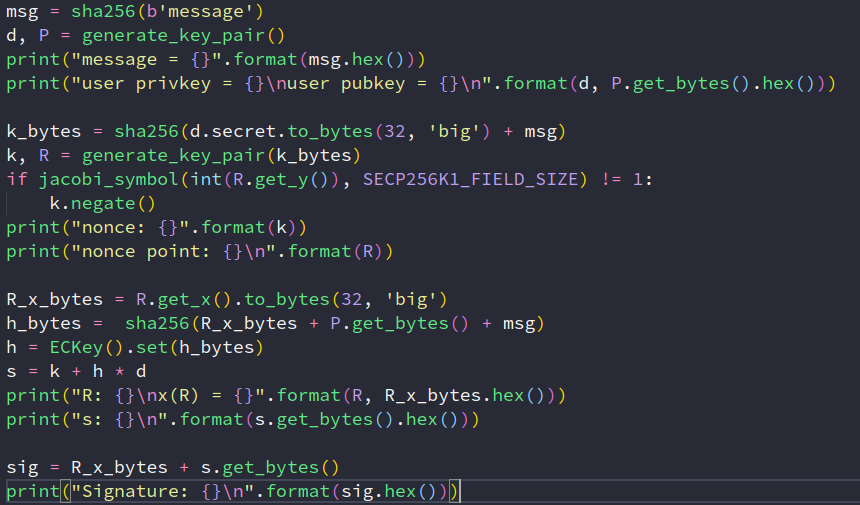
Schnorr 签名的结果如下：

message = ab530a13e45914982b79f9b7e3fba994cfd1f3fb22f71cea1afbf02b460c6d1d
user privkey = 40811356790294382983149959962124660206130438370548668724053064036307538116679
user pubkey = 0374248e7fdb13546ac94d961365aff6d352c413dd79b2056a2bb60f2971e79fc6

nonce: 55221941004635623701832462325081428209726520449893387818054719258463597914212
nonce point: 039c5530a2e78faa9a87d12ea48f201cec4462e21237ee6e682c935a28a44b826d

R: 039c5530a2e78faa9a87d12ea48f201cec4462e21237ee6e682c935a28a44b826d
x(R) = 9c5530a2e78faa9a87d12ea48f201cec4462e21237ee6e682c935a28a44b826d
s: 2265af70948f333f49fd1f4d38b4791cb8682f05d9719e5f482ef99b7dff790d

Signature: 9c5530a2e78faa9a87d12ea48f201cec4462e21237ee6e682c935a28a44b826d2265af70948f333f49fd1f4d38b4791cb8682f05d9719e5f482ef99b7dff790d

验证签名

​ 任何人可以在不知道随机数 k 和私钥 d 的情况下验证 Schnorr 签名。验证者所知道的是 G-椭圆曲线，H()-哈希函数，m-要签名的消息，P-公钥，x(R) 和 s-Schnorr 签名。验证方程：S = R + H(x(R) | P | m) * P。如果这个等式为真，则签名有效。

​ 推导这个过程，包含一个极其重要的理论：椭圆曲线中的点之间没有涉及除法。

1. s = k + H(m | R | P) d，如果方程两边都乘上椭圆曲线 G，则有：

2. sroomG = karmG + H(m | R | P) * d * G，因为 R = k* G, P = x* G，则有：

3. sSecretG = R + H(m | R | P) * P，椭圆曲线不能进行除法，因此，如果第 3 步的方程无法推导回第 1 步，k 的值和 x 的私钥将不会暴露。同时，方程验证也完成。

为什么非对称随机数是必要的

​ 如果我们只对消息 m 进行签名，则 h = H(P | m)，我们得到标量 s = h* d。由于没有随机数，我们得到 32 位的 Schnorr 签名 S = s = h*d。对于这个结果，计算是否 S = H(P | m) * P 是有效的，我们可以像往常一样验证签名是否有效。

​ 但在这种情况下，任何人都可以计算出私钥 d，因为 s 为标量，因此 d = s / h 可以轻易计算；如果添加一个随机数 k，则必须解决 d = (s-k) / h，但随机数 k 是未知的，因此这一计算是不可行的，这解释了为什么需要引入随机数。

基于 Schnorr 签名的 Musig 实现

​ 由于椭圆曲线上的点可以线性相加，因此多个用户的随机数和公钥可以线性相加，从而生成聚合随机数和聚合公钥。因此，“聚合账户”的概念应运而生。使用这个“聚合账户”来完成上述 Schnorr 签名的过程基本上与普通账户的 Schnorr 签名步骤相同。因此，在将 Schnorr 签名引入比特币主网络之后，聚合签名与普通交易在事务结果上没有区别，这在很大程度上保护了参与聚合签名的用户的隐私。

​ 聚合 Musig 方案由两部分组成，聚合公钥和聚合随机数，以及签名。聚合公钥的离线过程不需要通信，而聚合随机数和签名的过程需要三轮通信（在 Musig2 方案下，已经改进为两轮通信，详见上一篇文章）。

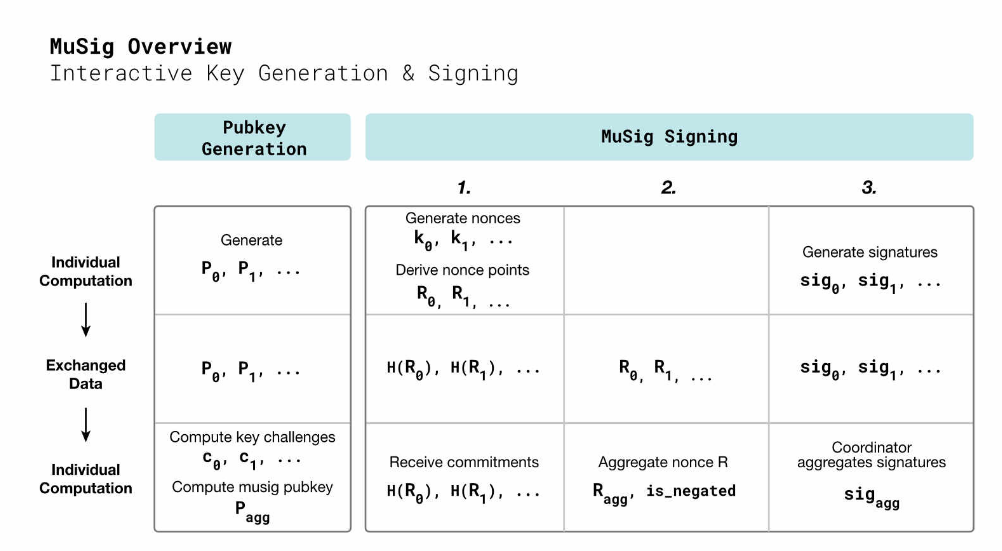
聚合公钥

​ 聚合公钥是将每个参与者的公钥线性相加。这个过程很容易完成，即 P_agg = P_0 + P_1 + ... + P_n，但需要考虑密钥抵消攻击。

密钥抵消攻击

​ 我们可以想象一个情景，Alice 和 Bob 想要生成 2-2 的聚合签名，为了达到聚合的目的，他们需要交换上述 Schnorr 签名所需的公钥和随机数。但如果 Bob 事先知道 Alice 的公钥 P_a 和随机数 R_a，那么当 Alice 计算签名时，Bob 可以通过发送 P'_b = P_b - P_a 和 R'_f = R_b - R_a 来欺骗 Alice。 随之而来。

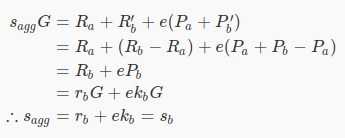
​ 从结果中可以看到，Alice 的 Ra 和 Pa 在最终签名结果中被抵消，这意味着 Bob 可以单独控制聚合签名的资产，这显然对 Alice 是危险的。

​ 当然，我们可以挑战 Bob 让他证明他拥有声明公钥 P 和随机数 R 的私钥标量，但这需要多一个通信轮次，因此我们可以通过添加挑战因子来调整参与者的公钥，以抵消密钥抵消攻击，具体如下：

​ 每个参与者的公钥通过挑战因子进行调整，挑战因子对于每个参与者都是唯一的，所有挑战因子是基于参与者的聚合公钥生成的，确保没有单个参与者（或参与者组）可以创建抵消其他参与者公钥的公钥。只要每个人都可以访问所有参与者的公钥（通过离线通信、协调等），挑战因子和聚合公钥可以在本地计算，而不需要额外的通信轮次。

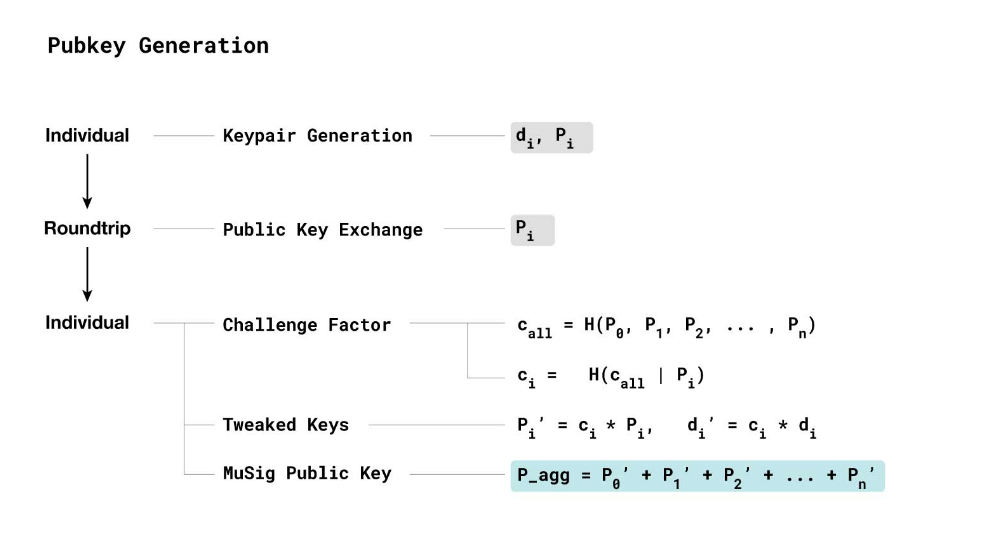
聚合随机数

​ 每个参与者必须生成自己的随机数 k_i 和随机数点 R_i（I = 0,1,...，表示参与者的顺序）。然后，参与者交换这些随机数点 R_i，并将所有随机数点 R_i 线性相加以生成聚合随机数点 R_agg。这个过程与上述聚合公钥相似，但不能像聚合公钥那样安全地进行验证，因为参与者的公钥保持不变，即使进行了多次签名且进行了离线协调，最终聚合公钥仍然是相同的。然而，随机数是不同的，每个签名过程中的随机数是不同的。为了避免在交换过程中出现欺骗，必然需要增加一个通信轮次。在这一轮通信中，参与者会交换随机数点 R_i 的哈希承诺。

​ 每个参与者在收到所有随机数点 R_i 的承诺之后，将交换随机数 R_i，并验证随机数 R_i 是否与提供的哈希承诺相匹配，如果相符。

​ 如果确认正确，则计算：符合模块 SECP256k1_FIELD_SIZE 的有效聚合随机数 R_agg 的二次剩余。

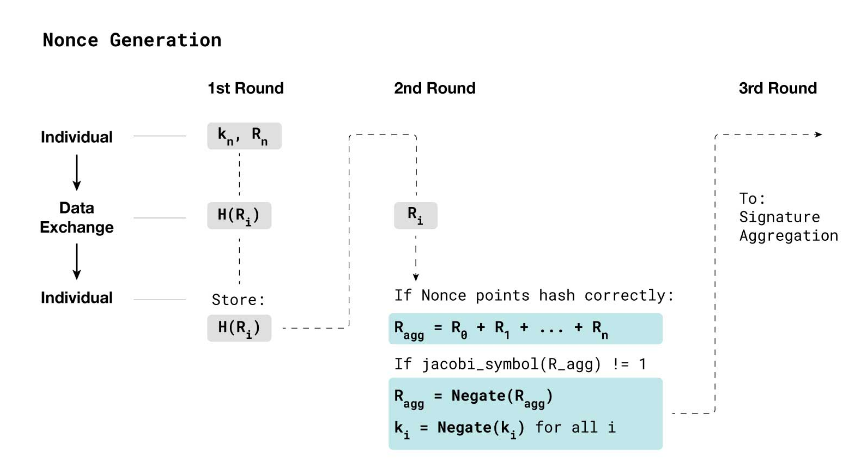
聚合签名

​ 每个参与者计算聚合公钥和聚合随机数后，就可以进行签名计算。每个参与者都有一个私钥 d_i 和一个随机数 k_i。通过计算标量 s_i = k_i + H(x(R_agg) | P_agg | m) * d_i 得到的结果是部分签名。最后，交换签名结果，将每个参与者的部分签名线性相加以生成最终的聚合签名。

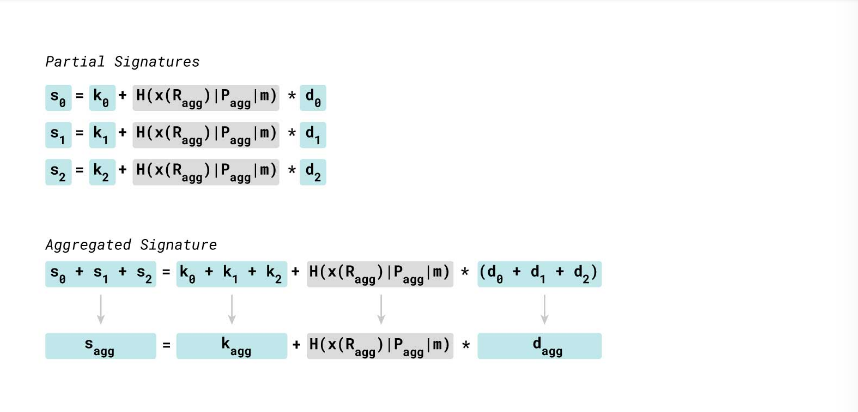
Musig 三轮通信的完整过程

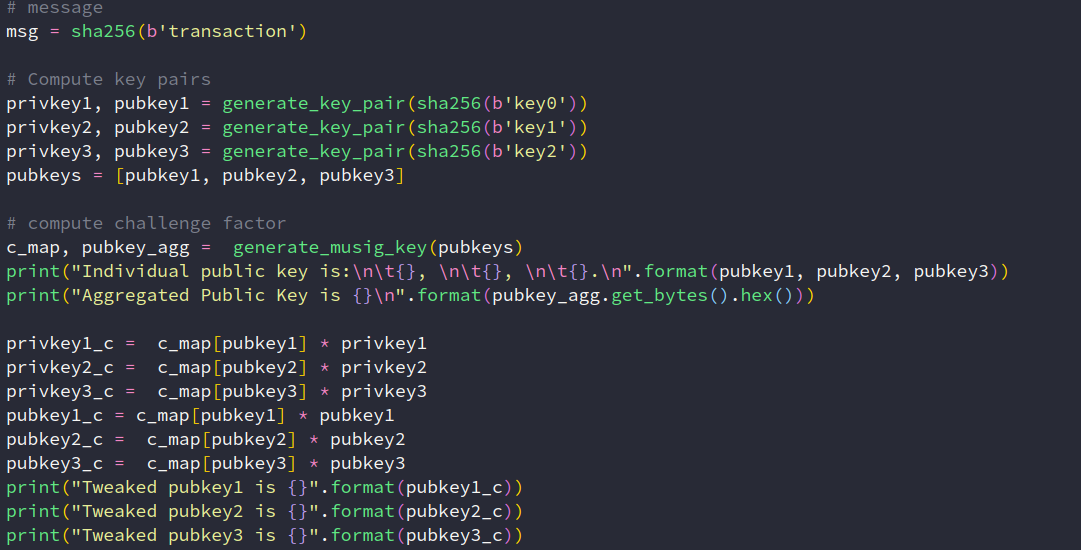
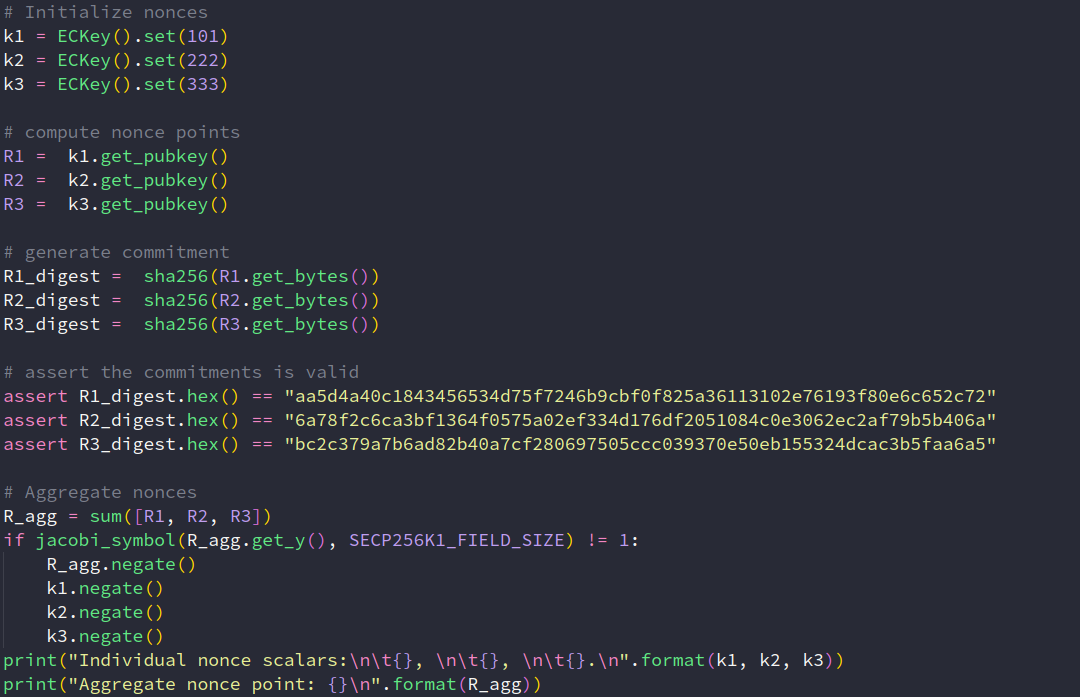
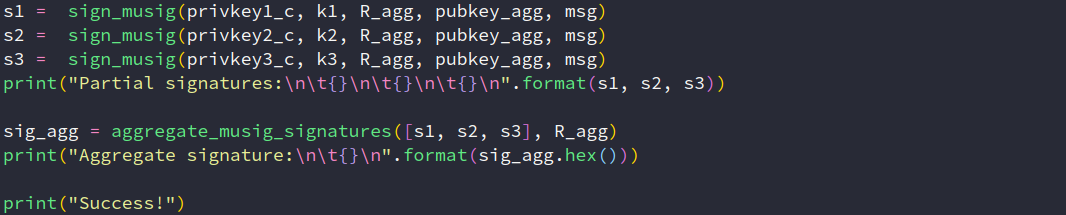
结果如下：

个人公钥是：
    026c5d5e73124f3c821c0985df787e11b3d018a86add577fa8661613a0d49dde59, 
    03f771877964fa2ce401d87bc2558a0df1e6921acef99389f059712b32cfda35fd, 
    03f039fdcdb728efbbddf4ee452419a988497debb7bd1b42644c5fa66e9af8c8b6。

聚合公钥是 02eeeea7d79f3ecde08d2a3c59f40eb3adcac9defb77d3b92053e5df95165139cd

调整后的 pubkey1 是 02066483b0841dba5821ee719178fb878102262cf505975e0a2d18e48c84b8362e
调整后的 pubkey2 是 0376e2769bcdc42a20e18cfa83125435c0cd1348a7849c6feebeb9394776cdcea6
调整后的 pubkey3 是 03bbc4110f3b28023f6ffefd29de76fe915029ce693f8fc3a1c327bdeb73940840
个人随机数标量：
    115792089237316195423570985008687907852837564279074904382605163141518161494236, 
    115792089237316195423570985008687907852837564279074904382605163141518161494115, 
    115792089237316195423570985008687907852837564279074904382605163141518161494004。

聚合随机数点： 03f90c3416d74049bf27b5563067c58401ff466e4bb04e1fa4d51ae4c93b4a8316

部分签名：
    65632340538892058604021005685526525791383877758802541334726676556343496273695
    49071424722101348040708779394444974474178306070453713897027096230295229616215
    40052638870461774859002446004708555184684360378078494722527781424448839071327

聚合签名：
    f90c3416d74049bf27b5563067c58401ff466e4bb04e1fa4d51ae4c93b4a83165625054ca06a0e7a76ecca379955370d56fa014fc1c0e62313dd4ed246b23494

成功！

• 原文链接： github.com/chainx-org/ch...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～