密码学101
椭圆曲线深入研究(第七部分)
- Frank Mangone
- 发布于 2025-05-21 08:55
- 阅读 2010
本文是关于配对(Pairings)的深入探讨文章的第一部分,介绍了配对的基本概念,即一种将两个群的元素作为输入并输出另一个群元素的双线性映射。
走到这里一定不容易。
我们已经涵盖了广泛的概念,从简单的东西到一些非常抽象的想法。
嗯,如果你觉得到目前为止事情已经很复杂了…… 好吧,抓住你手边的任何东西。 事情将变得非常疯狂。

因为今天,我们将讨论 配对。 与我之前关于该主题的文章形成鲜明对比的是,这次我们将深入了解更精细和具体的细节。
因此,配对将在 连续两次交付 中解决:第一部分(本文)将侧重于建立一些基础,我们将在第二部分(下一篇文章)中定义配对。
这将是很长的一篇文章。 深吸一口气。 喝杯咖啡。 准备好了吗? 让我们开始吧。
配对概览
首先,什么是配对?
通俗地说,配对 或 双线性映射 是一个函数,它接受两个输入,每个输入属于一个群,并输出另一个群的元素。 更正式地说,我们写成:
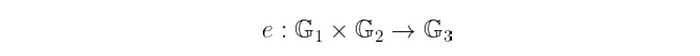
现在,这不仅仅是任何一种函数——要使其成为配对,它必须具有非常特殊的性质。 这种性质称为 双线性:这意味着它在两个输入中都是 线性的。
这是什么意思? 假设群运算可以分别用 𝔾 ₁、𝔾 ₂ 和 𝔾 ₃ 的 +、· 和 * 表示。 双线性本质上意味着以下两个等式都成立:
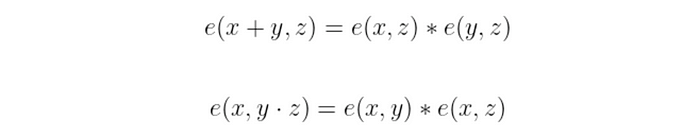
我知道,这看起来并没有那么疯狂。 但是这个特性使得可以巧妙地四处移动东西。 例如,很容易看出:
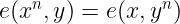
我随意使用了指数表示法,因为我们总能找到与乘法的同构。 但请记住,指数表示重复应用群运算。
这些我们可以使用配对进行的小技巧可以实现各种很酷的密码学原语,例如 基于身份的加密 (IBE) 和对于一些现代零知识证明至关重要的工具。 当然,还有其他的。
而这就是简单部分的结束。

现在的问题是我们需要找到 合适的群,并定义一些 函数,使其表现得像双线性映射。 当然,我们可以推断出这些群与我们值得信赖的椭圆曲线有关。 但这不像仅仅选择两条随机曲线那么简单——我们需要更多才能使其工作。
特别是,我们需要再次回顾椭圆曲线群的群结构。
椭圆曲线子群
在前一篇文章中,我们探讨了椭圆曲线群的结构如何可以用 Mordell-Weil 定理来描述:
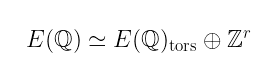
我们可以将其分为 无限阶 的子群(与整数同构)和 有限阶 的子群。
正如我们所知,有限域上的椭圆曲线群是有限的——在 p × p 网格上只能容纳这么多点。 因此,那些无限阶子群对我们来说并不是那么重要——将注意力集中在有限阶子群上更有意义。
通过按适当的系数缩放曲线,我们可以确保这些有限子群中的每个点不仅是合理的,而且是 整数值。 这就是我们获得有限域上的椭圆曲线群的方式。
我们关注的这些子群非常特殊,并且有自己的名称:它们被称为 挠群。
它们正是我们构建配对所需要的。
挠群
挠群是这样的子群,对于某个整数 r,其所有元素 P 都具有乘以 r 时得到 𝒪 的性质。 所以基本上,对于子群中的每个点,[r]P = 𝒪。 我们将其写为 E[r]——E 的 r-挠。
此外,如果 P 是 E[r] 的生成元,我们可以看到子群中的每个其他点也属于挠群,因为 [r]([n]P) = [n]([r]P) = [n] 𝒪 = 𝒪 .
因此,群 E[r] 也是映射 [r]: P → P 或乘以 r 的 核。 请记住,核只是 根 的广义概念。
现在我们回到有限域。 如前所述,很明显,整个椭圆曲线群是有限的。 然而,值得记住的是,正如我们在上一篇文章中探讨的那样,在椭圆曲线上找到整数值点是非常重要的。
同样很明显,由于我们可以使用的点数量有限,因此我们保证会有一些循环子群。 最多,整个群将是一些大小为 r 的单个循环。
接下来的是非常令人困惑的。 有一个定理,称为 有限阿贝尔群的结构定理(这是一个很长的名称),指出:
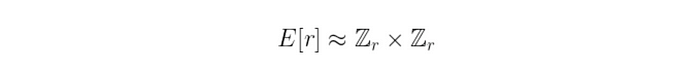
这意味着这两个群之间存在某种同构,这也意味着它们具有相同的大小(这是一一对应的关系)。
想想这会产生什么后果。 也就是说,r-挠应该具有 r² 的大小。 如果 r 大于 p(我们有限域的大小),我们甚至没有那么多可用的点!
因此,寻找这些剩余的点迫使我们查看 域扩展。
扩展曲线
使用域扩展对我们来说并不是一个新概念。 我们已经知道它是如何工作的:我们将一些元素附加到我们的有限域,导致它变得更大。 其中一个例子是 复数扩展:通过将 i 添加到域中——使得 i² + 1 = 0 ——,突然在扩展域中出现了无数个新的(复数)数字,并且它的大小增长到 p²。
同样,也有更多可用的点。 其中一些也满足椭圆曲线方程 E,因此椭圆曲线群的大小 也增加了。
复数在这里有点 显而易见的选择 ——但它们不是 唯一可用的选择。 事实上,我们可以实现任何大小为 pᵏ 的扩展,其中 k 是一个称为扩展 度 的整数。
我想在这里精确一点。 让我们再次使用 𝔽₁₇。 假设我们想通过添加一个元素 α 来扩展该域,使...
