与独裁者共处:变形密码学
- asecuritysite
- 发布于 2025-04-21 18:35
- 阅读 2083
本文介绍了变形密码学的概念,它允许对同一密文进行不同的解密,使得在“独裁者”审查的环境下,可以向审查者显示无害信息,同时秘密接收者可以解密出真实信息。文章通过ElGamal算法演示了变形密码学的实现,并提供了相应的Python代码示例。

与独裁者共存:变形密码学
上周,我花了一个小时与强大的 Moti Yung 进行了精彩的对话 [ 这里],他概述了变形密码学的用法:

他还在 2022 年发表了一篇经典论文 [ 这里]:

通过变形图像,我们可以移动到不同的视角并看到不同的图像。例如 [ 这里]:

在网络安全中,我们可以使用变形密码学来改变密码的视角。有了这个,我们假设我们有一个独裁者会读取我们所有的加密数据,因此会拥有一个密钥 sk。独裁者(Mallory)会逮捕任何发送他们无法读取的秘密信息的人。为此,Bob 可以创建两个密钥:sk0 和 sk1。他将 sk0 发送给 Mallory,将 sk1 发送给 Alice(Bob 想要发送秘密信息的人)。就 Mallory 而言,他拥有密文的唯一密钥。
然后我们有一个公钥 Pk 和两个私钥 sk0 和 sk1。然后 Bob 有两条消息:
msg0="我爱独裁者"
msg1="我恨独裁者"然后 Bob 使用公钥加密这两条消息:
CT=Enc(pk,msg0, msg1)然后独裁者将使用 sk0 解密并显示第一条消息:
Dec(sk0,CT) -> m0Alice 将使用她的密钥解密并显示第二条消息:
Dec(sk1,CT)-> m1因此,独裁者认为他们可以解密消息,并得到“我爱独裁者”。 然而,Alice 能够将密文解密为另一条消息“我恨独裁者”。
有一些方法支持创建变形加密,例如 RSA-OAEP、Pailler、Goldwasser-Micali、ElGamal 方案、Cramer-Shoup 和基于 Smooth Projective Hash 的系统 [ 这里]。 在这种情况下,我们将使用 ElGamal 方法。
ElGamal
使用 ElGamal 方法,我们创建一个密钥 sk,然后是一个公钥:
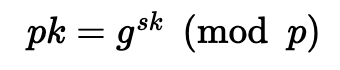
其中 g 是离散对数的基础,p 是一个素数。 对于消息 m,密码是:
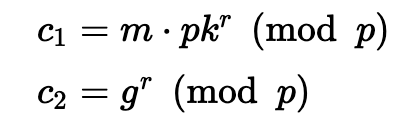
要解密,我们执行:
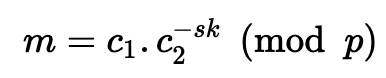
[2] 中的论文然后使用以下内容定义了用于变形密码学的 ElGamal 方法:

示例代码是 [ 这里}:\ \
import random
from Crypto.Cipher import AES
from Crypto.Random import get_random_bytes
class PublicParams:
def __init__(self, p, q, g):
self.p = p
self.q = q
self.g = g
class AnamParams:
def __init__(self, l, s, t):
self.F = lambda pp, K, x, y: \
int.from_bytes(AES.new(K, AES.MODE_ECB) \
.encrypt(x.to_bytes(8, 'little') \
+ y.to_bytes(8, 'little')), "little") % pp.p
self.d = lambda ap, x: x % ap.t
self.l = l
self.s = s
self.t = t
class KeyPair:
def __init__(self, sk, pk):
self.sk = sk
self.pk = pk
class DoubleKey:
def __init__(self, K, T, pk):
self.K = K
self.T = T
self.pk = pk
def Gen(pp):
sk = random.randint(0, pp.q - 1)
pk = pow(pp.g, sk, pp.p)
return KeyPair(sk, pk)
def Enc(pp, pk, msg):
r = random.randint(0, pp.q - 1)
c0 = (msg * pow(pk, r, pp.p)) % pp.p
c1 = pow(pp.g, r, pp.p)
return c0, c1
def Dec(pp, sk, c):
return (c[0] * pow(c[1], -sk, pp.p)) % pp.p
def aGen(pp, ap, pk):
K = get_random_bytes(16)
T = dict()
for i in range(ap.l):
T[pow(pp.g, i, pp.p)] = i
return DoubleKey(K, T, pk)
def aEncCtr(pp, ap, dk, msg, cm, ctr):
found = False
for x in range(ctr[0], ap.s):
for y in range(ctr[1], ap.t):
t = ap.F(pp, dk.K, x, y)
r = (cm + t) % pp.q
if ap.d(ap, pow(pp.g, r, pp.p)) == y:
found = True
break
if found:
break
ctr[1] = 0
ctr[0] = (x + (1 if y == ap.t - 1 else 0)) % ap.s
ctr[1] = (y + 1) % ap.t
c0 = (msg * pow(dk.pk, r, pp.p)) % pp.p
c1 = pow(pp.g, r, pp.p)
ctx = (c0, c1)
return ctx, ctr
def aEnc(pp, ap, dk, msg, cm):
while True:
x = random.randint(0, ap.s - 1)
y = random.randint(0, ap.t - 1)
t = ap.F(pp, dk.K, x, y)
r = (cm + t) % pp.q
if ap.d(ap, pow(pp.g, r, pp.p)) == y:
break
c0 = (msg * pow(dk.pk, r, pp.p)) % pp.p
c1 = pow(pp.g, r, pp.p)
ctx = (c0, c1)
return ctx
def aDec(pp, ap, dk, ctx):
y = ap.d(ap, ctx[1])
for x in range(ap.s):
t = ap.F(pp, dk.K, x, y)
s = (ctx[1] * pow(pp.g, -t, pp.p)) % pp.p
if s in dk.T:
return dk.T[s]
return -1
## Settings
runs = 1
## Public Parameters (safe prime, pow(g, (p - 1) // 2, p) != 1)
##p, g = int("0xFFFFFFFFFFFFFFFFC90FDAA22168C234C4C6628B80DC1CD1\
##29024E088A67CC74020BBEA63B139B22514A08798E3404DD\
##EF9519B3CD3A431B302B0A6DF25F14374FE1356D6D51C245\
##E485B576625E7EC6F44C42E9A637ED6B0BFF5CB6F406B7ED\
##EE386BFB5A899FA5AE9F24117C4B1FE649286651ECE65381\
##FFFFFFFFFFFFFFFF", 0), 5 # Oakley group (RFC 2409)
p, g = 1000000007, 5
q = p - 1
pp = PublicParams(p, q, g)
print("p =", pp.p)
print("q =", pp.q)
print("g =", pp.g)
## Anamorphic Parameters
l = 100
s = 100
t = 100
ap = AnamParams(l, s, t)
print("l =", ap.l)
print("s =", ap.t)
print("t =", ap.s)
## Keys Generation
kp = Gen(pp)
dk = aGen(pp, ap, kp.pk)
print("(sk, pk) = (%d, %d)" % (kp.sk, kp.pk))
print("K =", dk.K)
print("T = [", ", ".join(str(a) + "->" + str(b) for (a,b) in \
sorted([((pp.g ** i) % pp.p, i) for i in range(l)])), ']')
## Testing aEnc -> Dec and aEnc -> aDec
msg = random.randint(1, pp.p - 1)
cm = random.randint(0, l - 1)
##ctr = [0, 0]
for i in range(runs):
#c, ctr = aEncCtr(pp, dk, msg, cm, ctr)
ctx = aEnc(pp, ap, dk, msg, cm)
msg_ = Dec(pp, kp.sk, ctx)
cm_ = aDec(pp, ap, dk, ctx)
print("(%d, %d) -> aEnc -> (%d, %d) -> Dec -> %d" \
% (msg, cm, ctx[0], ctx[1], msg_))
print("(%d, %d) -> aEnc -> (%d, %d) -> aDec -> %d" \
% (msg, cm, ctx[0], ctx[1], cm_))
## Testing Enc -> Dec and Enc -> aDec
for i in range(runs):
m = random.randint(1, pp.p - 1)
ctx = Enc(pp, kp.pk, m)
msg_ = Dec(pp, kp.sk, ctx)
cm_ = aDec(pp, ap, dk, ctx)
print("%d -> Enc -> (%d, %d) -> Dec -> %d" \
% (m, ctx[0], ctx[1], msg_))
print("%d -> Enc -> (%d, %d) -> aDec -> %d" \
% (m, ctx[0], ctx[1], cm_), "(!)" if cm_ != -1 else "")一次示例运行是:
p = 1000000007
q = 1000000006
g = 5
l = 100
s = 100
t = 100
(sk, pk) = (808381696, 432452453)
K = b'\x8a\x96\xbe\x94:\x1d\x9a\x0e`1|?\x16D]N'
T = [ 1->0, 5->1, 25->2, 125->3, 625->4, 3125->5, 15625->6, 78125->7, 390625->8, 1953125->9, 9765625->10, 18207916->80, 26761407->94, 27912589->38, 48828125->11, 55390767->72, 91039580->81, 96145664->77, 102694758->31, 103515583->14, 110488626->68, 133807035->95, 134200073->44, 139562945->39, 154865266->21, 171376783->64, 184223302->35, 220538953->30, 220703118->13, 226840016->43, 234275358->63, 244107792->29, 244140625->12, 246855073->62, 249371016->61, 275989486->83, 276953835->73, 284419547->66, 335688566->89, 339598996->57, 345175854->97, 355001804->46, 358158117->24, 375225192->49, 379947423->84, 380629737->51, 384769168->74, 392214094->91, 403641586->79, 422097728->67, 430973056->20, 445368006->42, 449874206->60, 455197900->82, 467137716->88, 467919802->56, 480728320->78, 486194614->19, 489073604->41, 489974844->59, 493427546->87, 498685512->86, 513473790->32, 515743362->53, 517577915->15, 552443130->69, 567368936->33, 578716796->54, 587889561->16, 605582522->37, 619229137->76, 629396294->99, 669035175->96, 671000365->45, 678442823->90, 697238927->18, 697814725->40, 697994973->58, 725879263->98, 762215636->70, 769764317->27, 774326330->22, 775009013->47, 790790578->25, 805352287->93, 811078159->71, 836844666->34, 848821564->28, 856883915->65, 871631629->23, 875045044->48, 876125953->50, 893583966->55, 899737108->85, 903148678->52, 921116510->36, 923845833->75, 939447791->17, 953952869->26, 961070463->92 ]
(4, 2) -> aEnc -> (929257589, 695009996) -> Dec -> 4
(4, 2) -> aEnc -> (929257589, 695009996) -> aDec -> 2
451787795 -> Enc -> (749003435, 140907022) -> Dec -> 451787795
451787795 -> Enc -> (749003435, 140907022) -> aDec -> -1在这种情况下,消息 1 是 4,消息 2 是 2。当我们解密时,我们得到 4,但是当我们进行变形解密时,我们得到 2。
你可以在这里运行代码:
变形密码学 \ 在网络安全中,我们可以使用变形密码学 [1] 来改变密码的视角。有了这个,我们假设… \ asecuritysite.com
结论
如果你有时间,请去听听 Moti 的演讲:
YouTube
Spotify: https://open.spotify.com/episode/0zsjAewJt8YnlB6g5Q1eZm?si=b6483c6f33df4285
Apple: https://podcasts.apple.com/gb/podcast/asecuritysite-podcast/id1617044319?i=1000703484352
参考
[1] Persiano, G., Phan, D. H., & Yung, M. (2022, May). Anamorphic encryption: private communication against a dictator. In Annual International Conference on the Theory and Applications of Cryptographic Techniques (pp. 34–63). Cham: Springer International Publishing.
[2] Banfi, F., Gegier, K., Hirt, M., Maurer, U., & Rito, G. (2024, May). Anamorphic encryption, revisited. In Annual International Conference on the Theory and Applications of Cryptographic Techniques (pp. 3–32). Cham: Springer Nature Switzerland.
- 原文链接: medium.com/asecuritysite...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 欺诈与生成式人工智能和代理人工智能的兴起 87 浏览
- 关于伊朗监控影响的好文章 163 浏览
- “夺旗”竞赛继续! 311 浏览
- 智能合约代理模式:2026 年安全指南 488 浏览
- zkMesh:2026年1月回顾 448 浏览
- 每个开发者都应该知道的Go高级技巧 (Go并发性能和最佳实践) 479 浏览
- 量子计算与区块链:匹配紧迫性与实际威胁 1105 浏览
- 我们如何确定Web3团队采用AI审计的投资回报率? 408 浏览
- Eloizer 介绍:Solana 程序的静态分析器 - Inversive Labs 459 浏览
- Secret Box、Sealed Box 还是 Box:选择你的加密方法 485 浏览
- 区块链钱包入门 612 浏览
- 使用 Move Prover 验证 Aptos Vault 的正确性 454 浏览

