移动电话网络、RFID和TETRA:最薄弱的环节?
- asecuritysite
- 发布于 2025-03-10 10:23
- 阅读 1641
本文讨论了移动通信网络、RFID和TETRA的加密弱点,特别关注了GPRS/GSM网络中使用的A5/1、A5/3(KASUMI)加密算法,SPECK在RFID通信中的应用以及TETRA标准中的TEA3加密算法。研究表明,由于GPU计算能力的增强,这些加密算法容易受到暴力破解攻击,强调了增加密钥长度至128位以上的重要性,并提出了在数据层进行加密的建议。

手机网络、RFID 和 TETRA:最薄弱的环节?
KUSAMI: 使用时间-内存-折衷表,通过 2400 个 RTX 4090 GPU 在 21 天内破解,对于暴力破解攻击,在 2400 个 RTX GPU 上花费了 38 小时。
那么,在你的智能手机上,你应该使用 WhatsApp 进行通话还是使用 GPRS/GSM 网络? WhatsApp 使用明确定义的加密标准,例如用于对称密钥加密的 AES,而 GPRS/GSM 网络使用 A5/3 方法来加密数据。不管你喜不喜欢,移动电话网络常常被设计成不安全的,因为使用的方法被故意保持较弱,以便执法机构可以破解它们。所有这些感觉就像 DES 密码被限制在 56 位的日子一样,因为执法部门可以破解这种大小的密钥。例如,过去,英国政府只希望移动电话网络中使用的原始加密使用 48 位。
所以,我现在正在阅读这篇论文 [4],并且 GPRS/GSM 网络的安全性已经变得非常不安全了 [ 这里]:

破解 KASUMI、SPECK 和 TEA3 的三个 CUDA 优化是:
- 直接方法——只是并行化密码中的操作;
- 基于表的方法——构建一个可能的共享计算区域的大空间;
- Bitsliced(位切片)——与其对字节使用 8 位操作,不如使用按位方法。
在该论文中,他们优化了 KASUMI(用于 GPRS/GSM)、SPECK(用于 RFID 通信)和 TEA3(用于 TETRA)以进行暴力破解攻击。有了这个,他们可以在 RTX 4090 GPU 上分别尝试每秒 2³⁵、2³⁶ 和 2³⁴ 个密钥。这比之前的破解尝试快了大约 15 倍 [3]。对于 KASUMI,研究人员发现需要 2,400 个 RTX 4090 GPU 才能在 20.6 天内破解一个密码,用于时间-内存-折衷 (TMTO) 表:
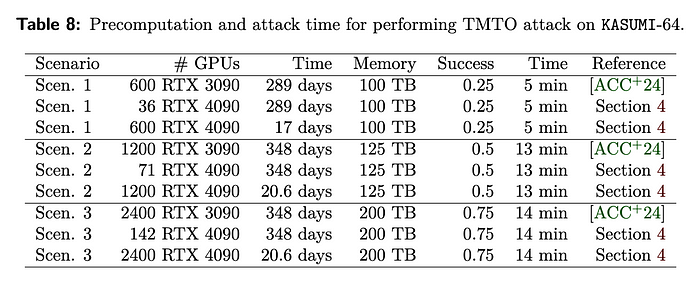
图:[4]
对于暴力破解攻击,仅需 2400 个 RTX GPU 运行 38 小时。使用 RTX 4090,我们有 16,384 个核心,它使用 Ada Lovelace 架构:
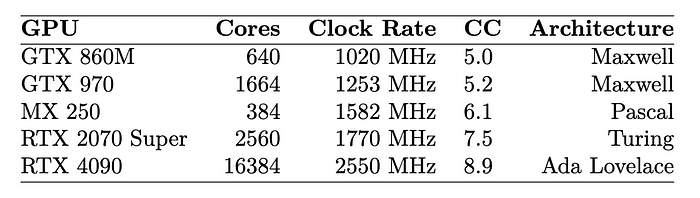
图:[4]
TEA3 用于 TETRA(陆地集群无线电)网络,世界各地的许多警察和军队都将其用于加密无线电。为此,论文定义:
用于集群无线电的欧洲标准 TETRA 使用专有的密钥流生成器,这些生成器已经保密了几十年。最近,它们被逆向工程,并且表明这些密钥流生成器中最好的一类使用了 80 位密钥。我们最好的优化表明,可以使用 136 万个 RTX 4090 GPU 在一年内将其破解。这是一个现实世界中的重要威胁,因为 TETRA 被军队、警察、紧急服务部门、监狱和政府机构使用。
结论是,由于 GPU 的进步,我们应该避免小于 128 位的密钥大小。
A5/1、A5/2 和 A5/3(KUSAMI)
虽然我们都专注于核心 IP 网络,并且它在空中传输中具有相对良好的保护,但可能是 GSM/3G 网络存在风险。移动电话网络通常使用 A5/1 或 A5/2 流加密方法,但几乎在其运行的第一天,它就成为了破解者的目标,并且破解 A5/2 的源代码在其公开后一个月内发布。虽然像 AES 这样的分组密码很强大,但 A5/1 流密码已被证明对某些类型的攻击很弱 [2]。
过去,各国在移动网络加密方面有两个主要选择:A5/1 和 A5/2。A5/2 是故意设计的较弱的,因此民族国家可以轻松破解密码,但通常在公开后一个月内就被破解了。A5/1 旨在更强大,但是,由于它的密钥相对较短,因此可以使用强大的计算机进行破解。目前,全球有数十亿台设备使用 A5/1 来保证安全,并且它们很可能被美国国家安全局 (NSA) 破解。
对于 A5/1,我们使用带有反馈的三个移位寄存器(图 1)。使用流密码,我们通常生成一个无限长的密钥流,然后将其与数据流进行异或 (EX-OR) 运算。
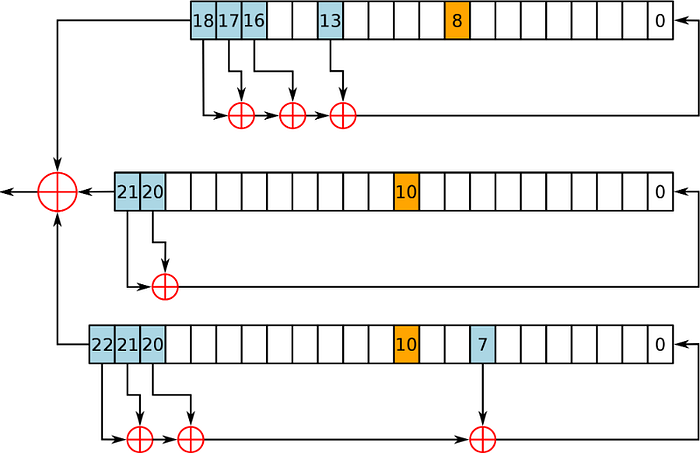
图 1:[1]
在第一个移位寄存器中,位置 18、17、16 和 13 处的位被异或在一起以产生一个新位,该新位被放置在末尾。这会推动所有位向左移动一个位置。然后,最后一位(位置 18 处的那一位)将被推出并与来自其他移位寄存器的输出进行异或运算。移位寄存器的长度分别为 19、22 和 23 位,因此使用的密钥长度为 64 位 (19+22+23)。在图中,位 8、10 和 10 被高亮显示,它们是时钟控制位。这些在每个周期都会被检查。在这些位中,1 的数量将多于 0 的数量,或者 0 的数量多于 1 的数量。具有最流行的位值的寄存器将使其位前进,而其他的则不会前进。
该算法本身在安装在 1 亿部手机中时一直保密,并且是 GSM(全球移动通信系统)标准的一部分,并且此后已成为 3G 标准(即使它被认为是弱的)。美国和欧洲采用了更强的 A5/1 算法,但许多国家选择了较弱的算法。它最终于 1999 年 8 月公开,并且在一个月内 A5/2 方法就被破解了。对于 A5/1,人们认为美国国家安全局 (NSA) 可以破解它(因为他们有计算能力来破解 64 位密钥)。
该攻击通常使用已知的明文攻击,但新的攻击现在允许实时解密密码流。当 1982 年首次提出时,人们认为 A5/1 密钥的长度为 128 位,但最终确定为 64 位密钥(可以使用昂贵的硬件通过暴力破解来破解)。政府的压力很可能迫使密钥变得更短。事实上,人们认为英国只想要 48 位,而当时的西德政府则推动更大的密钥大小(因为他们担心东德政府能够破解他们的密码)。 流密码允许自动同步,并且可以接收到每个位时对其进行解码。 演示在此:
SRLabs(安全研究实验室)专注于从移动电话网络捕获数据并破解 A5/1 加密。他们从通信中获取两个加密的已知明文消息,然后使用他们的 Kraken 实用程序在几秒钟内以 90% 的成功率找到密钥,使用的是一组彩虹表(总大小为 40 个表,每个表 2TB)[这里]。
Gendrullis 等人 [2] 使用并行处理系统在几个小时内破解了 A5/1,但现在在云中运行的 NVIDIA GPU 可以实现相同的结果,但成本明显更低。
A5/3
A5/3 加密系统——被称为 KASUMI ——日语中“雾”的意思——是 A5/1 的升级版,并使用分组密码。 A5/1 旨在用于 GSM 网络,而 A5/3 用于 3GPP,并且基于三菱创建(并获得专利)的 MISTY1 密码,但经过修改以减少对移动设备的处理限制。
Key(密钥)应为 32 个字符(128 位),数据应为 16 个字符(64 位)的倍数。 2010 年,研究人员(Orr Dunkelman、Nathan Keller 和 Adi Shamir)表明,Kasumi 可以通过相关的密钥攻击来破解。如果标准组织坚持使用原始的 MISTY1 规范,则攻击是不可能实现的。 KASUMI 使用 16x32 的 S 盒方法来对数据进行运算,并具有 128 位的初始化向量。
对 A5/3 的一项更新的攻击——三明治攻击——表明可以使用“未优化的 PC”破解 A5/3,在几分钟内恢复 96 个密钥位,并在 两小时内 恢复剩余的 128 位密钥。

这里 有一个演示,它基于 https://github.com/bozhu/KASUMI-Python: 的 Python 代码:
key = 0x9900aabbccddeeff1122334455667788
text = 0xfedcba0987654321
def _bitlen(x):
assert x >= 0
return len(bin(x)) - 2
def _shift(x, s):
assert _bitlen(x) <= 16
return ((x << s) & 0xFFFF) | (x >> (16 - s))
def _mod(x):
return ((x - 1) % 8) + 1S7 = (
54, 50, 62, 56, 22, 34, 94, 96, 38, 6, 63, 93, 2, 18,123, 33,
55,113, 39,114, 21, 67, 65, 12, 47, 73, 46, 27, 25,111,124, 81,
53, 9,121, 79, 52, 60, 58, 48,101,127, 40,120,104, 70, 71, 43,
20,122, 72, 61, 23,109, 13,100, 77, 1, 16, 7, 82, 10,105, 98,
117,116, 76, 11, 89,106, 0,125,118, 99, 86, 69, 30, 57,126, 87,
112, 51, 17, 5, 95, 14, 90, 84, 91, 8, 35,103, 32, 97, 28, 66,
102, 31, 26, 45, 75, 4, 85, 92, 37, 74, 80, 49, 68, 29,115, 44,
64,107,108, 24,110, 83, 36, 78, 42, 19, 15, 41, 88,119, 59, 3,
)S9 = (
167,239,161,379,391,334, 9,338, 38,226, 48,358,452,385, 90,397,
183,253,147,331,415,340, 51,362,306,500,262, 82,216,159,356,177,
175,241,489, 37,206, 17, 0,333, 44,254,378, 58,143,220, 81,400,
95, 3,315,245, 54,235,218,405,472,264,172,494,371,290,399, 76,
165,197,395,121,257,480,423,212,240, 28,462,176,406,507,288,223,
501,407,249,265, 89,186,221,428,164, 74,440,196,458,421,350,163,
232,158,134,354, 13,250,491,142,191, 69,193,425,152,227,366,135,
344,300,276,242,437,320,113,278, 11,243, 87,317, 36, 93,496, 27,
487,446,482, 41, 68,156,457,131,326,403,339, 20, 39,115,442,124,
475,384,508, 53,112,170,479,151,126,169, 73,268,279,321,168,364,
363,292, 46,499,393,327,324, 24,456,267,157,460,488,426,309,229,
439,506,208,271,349,401,434,236, 16,209,359, 52, 56,120,199,277,
465,416,252,287,246, 6, 83,305,420,345,153,502, 65, 61,244,282,
173,222,418, 67,386,368,261,101,476,291,195,430, 49, 79,166,330,
280,383,373,128,382,408,155,495,367,388,274,107,459,417, 62,454,
132,225,203,316,234, 14,301, 91,503,286,424,211,347,307,140,374,
35,103,125,427, 19,214,453,146,498,314,444,230,256,329,198,285,
50,116, 78,410, 10,205,510,171,231, 45,139,467, 29, 86,505, 32,
72, 26,342,150,313,490,431,238,411,325,149,473, 40,119,174,355,
185,233,389, 71,448,273,372, 55,110,178,322, 12,469,392,369,190,
1,109,375,137,181, 88, 75,308,260,484, 98,272,370,275,412,111,
336,318, 4,504,492,259,304, 77,337,435, 21,357,303,332,483, 18,
47, 85, 25,497,474,289,100,269,296,478,270,106, 31,104,433, 84,
414,486,394, 96, 99,154,511,148,413,361,409,255,162,215,302,201,
266,351,343,144,441,365,108,298,251, 34,182,509,138,210,335,133,
311,352,328,141,396,346,123,319,450,281,429,228,443,481, 92,404,
485,422,248,297, 23,213,130,466, 22,217,283, 70,294,360,419,127,
312,377, 7,468,194, 2,117,295,463,258,224,447,247,187, 80,398,
284,353,105,390,299,471,470,184, 57,200,348, 63,204,188, 33,451,
97, 30,310,219, 94,160,129,493, 64,179,263,102,189,207,114,402,
438,477,387,122,192, 42,381, 5,145,118,180,449,293,323,136,380,
43, 66, 60,455,341,445,202,432, 8,237, 15,376,436,464, 59,461,
)
class Kasumi:
def __init__(self):
self.key_KL1 = [None] * 9
self.key_KL2 = [None] * 9
self.key_KO1 = [None] * 9
self.key_KO2 = [None] * 9
self.key_KO3 = [None] * 9
self.key_KI1 = [None] * 9
self.key_KI2 = [None] * 9
self.key_KI3 = [None] * 9
def set_key(self, master_key):
assert _bitlen(master_key) <= 128
key = [None] * 9
key_prime = [None] * 9
master_key_prime = master_key ^ 0x0123456789ABCDEFFEDCBA9876543210
for i in range(1, 9):
key[i] = (master_key >> (16 * (8 - i))) & 0xFFFF
key_prime[i] = (master_key_prime >> (16 * (8 - i))) & 0xFFFF
for i in range(1, 9):
self.key_KL1[i] = _shift(key[_mod(i + 0)], 1)
self.key_KL2[i] = key_prime[_mod(i + 2)]
self.key_KO1[i] = _shift(key[_mod(i + 1)], 5)
self.key_KO2[i] = _shift(key[_mod(i + 5)], 8)
self.key_KO3[i] = _shift(key[_mod(i + 6)], 13)
self.key_KI1[i] = key_prime[_mod(i + 4)]
self.key_KI2[i] = key_prime[_mod(i + 3)]
self.key_KI3[i] = key_prime[_mod(i + 7)]
def fun_FI(self, input, round_key):
# assert _bitlen(input) <= 16
left = input >> 7
right = input & 0b1111111
round_key_1 = round_key >> 9
round_key_2 = round_key & 0b111111111
tmp_l = right
# assert _bitlen(left) <= 9
tmp_r = S9[left] ^ right
left = tmp_r ^ round_key_2
# assert _bitlen(tmp_l) <= 7
right = S7[tmp_l] ^ (tmp_r & 0b1111111) ^ round_key_1
tmp_l = right
# assert _bitlen(left) <= 9
tmp_r = S9[left] ^ right
# assert _bitlen(tmp_l) <= 7
left = S7[tmp_l] ^ (tmp_r & 0b1111111)
right = tmp_r
# assert _bitlen(left) <= 7
# assert _bitlen(right) <= 9
return (left << 9) | right
def fun_FO(self, input, round_i):
# assert _bitlen(input) <= 32
# assert round_i >= 1 and round_i <= 8
in_left = input >> 16
in_right = input & 0xFFFF
out_left = in_right # this is not Feistel at all, maybe not reversible
out_right = self.fun_FI(in_left ^ self.key_KO1[round_i],
self.key_KI1[round_i]) ^ in_right
in_left = out_right # use in_* as temp variables
in_right = self.fun_FI(out_left ^ self.key_KO2[round_i],
self.key_KI2[round_i]) ^ out_right
out_left = in_right
out_right = self.fun_FI(in_left ^ self.key_KO3[round_i],
self.key_KI3[round_i]) ^ in_right
# assert _bitlen(out_left) <= 16
# assert _bitlen(out_right) <= 16
return (out_left << 16) | out_right
def fun_FL(self, input, round_i):
# assert _bitlen(input) <= 32
# assert round_i >= 1 and round_i <= 8
in_left = input >> 16
in_right = input & 0xFFFF
out_right = in_right ^ _shift(in_left & self.key_KL1[round_i], 1)
out_left = in_left ^ _shift(out_right | self.key_KL2[round_i], 1)
# assert _bitlen(out_left) <= 16
# assert _bitlen(out_right) <= 16
return (out_left << 16) | out_right
def fun_f(self, input, round_i):
# assert _bitlen(input) <= 32
# assert round_i >= 1 and round_i <= 8
if round_i % 2 == 1:
state = self.fun_FL(input, round_i)
output = self.fun_FO(state, round_i)
else:
state = self.fun_FO(input, round_i)
output = self.fun_FL(state, round_i)
# assert _bitlen(output) <= 32
return output
def enc_1r(self, in_left, in_right, round_i):
# assert _bitlen(in_left) <= 32
# assert _bitlen(in_right) <= 32
# assert round_i >= 1 and round_i <= 8
out_right = in_left # note this is different from normal Feistel
out_left = in_right ^ self.fun_f(in_left, round_i)
# assert _bitlen(out_left) <= 32
# assert _bitlen(out_right) <= 32
return out_left, out_right
def dec_1r(self, in_left, in_right, round_i):
# assert _bitlen(in_left) <= 32
# assert _bitlen(in_right) <= 32
# assert round_i >= 1 and round_i <= 8
out_left = in_right
out_right = self.fun_f(in_right, round_i) ^ in_left
# assert _bitlen(out_left) <= 32
# assert _bitlen(out_right) <= 32
return out_left, out_right
def enc(self, plaintext):
assert _bitlen(plaintext) <= 64
left = plaintext >> 32
right = plaintext & 0xFFFFFFFF
for i in range(1, 9):
left, right = self.enc_1r(left, right, i)
return (left << 32) | right
def dec(self, ciphertext):
assert _bitlen(ciphertext) <= 64
left = ciphertext >> 32
right = ciphertext & 0xFFFFFFFF
for i in range(8, 0, -1):
left, right = self.dec_1r(left, right, i)
return (left << 32) | rightprint "Data is "+hex(text)
print "Key is "+hex(key)
my_kasumi = Kasumi()
my_kasumi.set_key(key)encrypted = my_kasumi.enc(text)
print 'encrypted', hex(encrypted)for i in range(99): # for testing
encrypted = my_kasumi.enc(encrypted)
for i in range(99):
encrypted = my_kasumi.dec(encrypted)decrypted = my_kasumi.dec(encrypted)
print 'decrypted', hex(decrypted)对于 4G LTE(以及取代传统的 No.7 信令系统 (SS7) 协议),使用的加密方法是 SNOW 1.0/2.0/3G。 这些是由 Thomas Johansson 和 Patrik Ekdahl(隆德大学)开发的同步流密码。 SNOW 3G 已被选择用于 3GPP 加密算法 UEA2 和 UIA2。 下图显示了 Snow 3G 的大致操作。 它使用 128 位密钥和 128 位 IV。 Snow 3G 是一种流密码,并使用带有 16 个 8 位单元的 LFSR,以及一个有限状态机 (FSM)。
SPECK
SPECK 是一种超轻量级分组密码,具有 32 位块(64 位密钥和 32 轮)或 64 位块(128 位密钥和 44 轮)。 它的密钥大小为 64、72、96、128、144、192 或 256 位,块大小为 32、48、64、96 或 128 位。 它针对软件实现中的性能进行了优化。
TETRA 标准
最近有报道称,TETRA(陆地集群无线电)标准 [ 这里] 在其密码学中存在许多漏洞。总体而言,TETRA 被世界各地的许多警察和军队用于加密无线电。这些漏洞已经存在了十多年,并可能导致敏感信息的泄露。
这些漏洞是由 Midnight Blue 发现的,并将于 2023 年 8 月 9 日在 Black Hat 2023 上以“Redacted Telecom Talk”的形式展示 [ 这里]。由于这项工作非常敏感,因此存在许多与其披露相关的问题,因此该演讲的完整详细信息尚未发布。但是,它涉及超过 18 个月的负责任的披露,涉及到破解从 eBay 购买的 TETRA 无线电。
TETRA 最初由欧洲电信标准协会 (ETSI) 于 1996 年标准化,并被摩托罗拉和空中客车等许多无线电制造商使用。它没有开源软件,并且依赖于秘密和专有的密码学。
TEA1——故意设计的弱加密
世界各国政府通常对密码学实行出口管制——以降低安全级别,以便他们自己的执法人员有很大的机会破解其自身境外加密的流量。其中最著名的一个与 Netscape 相关,它创建了 TLS(传输层安全性)的原始版本,该版本为网页创建了一个安全通道——我们现在在我们的大多数 Web 访问中看到的 HTTPs。
但是,由于出口管制,这降低了安全级别——使用的 RSA 方法仅设置为 512 位(现在很容易破解)。由于此密钥用于传递安全隧道中使用的加密密钥,这意味着代理可以破坏 HTTPs 通信的通信通道。自那时以来,我们已经为这种弱化付出了代价——并出现了 Freak 和 BEAST 等漏洞。TETRA 中的漏洞也与类似的问题有关,例如为了符合出口管制而降低密码学的强度。在 TERTA 中,TEA1 方法将密钥大小减少到 80 位,并且与其他漏洞一起,允许使用标准笔记本电脑在几分钟内破解加密流量。
除此之外,研究人员还发现了 TETRA 方法的其他漏洞,这些漏洞泄露了敏感信息——包括历史通信中的信息。核心的漏洞涉及到从无线电上的主接口跳出,然后通过在该过程中执行恶意代码,然后执行到信号处理器和 wifi 硬件。设备上的这个主芯片然后包含一个安全的 enclave,用于存储主要的加密密钥。该团队能够访问此芯片并发现所使用的密码学方法和相关的构
- 原文链接: billatnapier.medium.com/...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 神奇的 Zig、C 和 OpenSSL 12 浏览
- Shamir份额的魔力:BLS门限签名 290 浏览
- zkMesh:2026年1月回顾 372 浏览
- FRI (and friends) 使用 Lean4 形式化验证 FRI(及相关内容) 365 浏览
- 量子计算与区块链:匹配紧迫性与实际威胁 799 浏览
- ZK 编年史:电路(第二部分) 373 浏览
- 有限域之美与力量 (以及 Zig) 466 浏览
- Secret Box、Sealed Box 还是 Box:选择你的加密方法 428 浏览
- 扳手攻击:发生与预防 500 浏览
- zkEVM 安全性概览 541 浏览
- 区块链钱包入门 545 浏览
- 基于哈希函数的签名(三):多次签名 653 浏览

