以太坊二叉树笔记

感谢 Guillaume 和 Vitalik 的讨论和反馈

介绍

这是对 L1 中二叉树的 全新 看法，其动机是最近的兴趣、线下讨论等。

EIP-3102 仍然存在，但它可能已经过时，因为它与 Verkle 中引入的更近期的想法（也适用于二叉树）不太吻合。 这可能会在试图公平地比较 Verkle 和二叉树时产生混淆。

这些笔记可能有助于其他核心开发者了解最新情况并更有效地参与讨论。本文档是个人总结，而不是正式提案——可能存在错误并且可以改进。 如果你有任何进一步的想法或改进，请联系！

形状 - 稀疏与前缀

二叉树主要有两种选择：

• 稀疏默克尔树 (SMT)：具有固定（完整）深度的树，深度为 256 位（假设密钥长度）。
• 带前缀的默克尔树 (PMT)：包括扩展节点以避免完整深度。

除了其他优点/缺点之外，SMT 很有吸引力，因为规范非常简单，这对于整体实现（尤其是用于有效性证明的电路）来说非常棒。 明显的权衡是拥有更大的树并需要更多的哈希，而 PMT 试图解决这个问题。

SMT 是一种真正的选择吗？

有两篇研究文章试图缓解一些“低效率”：

• 优化稀疏默克尔树
• 一种在零输入时几乎微不足道的 32 字节长抗冲突哈希函数

这些并非 新 的突破 (~2019)，但也许并非每个人都知道它们，这是在编写这些笔记时巩固/扩展它们的动机之一。 我建议阅读原始讨论，但我将进行总结，以便为其他人提供更线性/紧凑的解释，并提供视觉效果以增强理解。 这并不意味着必须使用这些想法； 如果它们有帮助，请考虑使用它们。

优化存储

给定一个 SMT，如果你选择一条通向非零叶子值的路径，你会发现经过一定的深度后，你会进入一个只有一个非零叶子的子树。

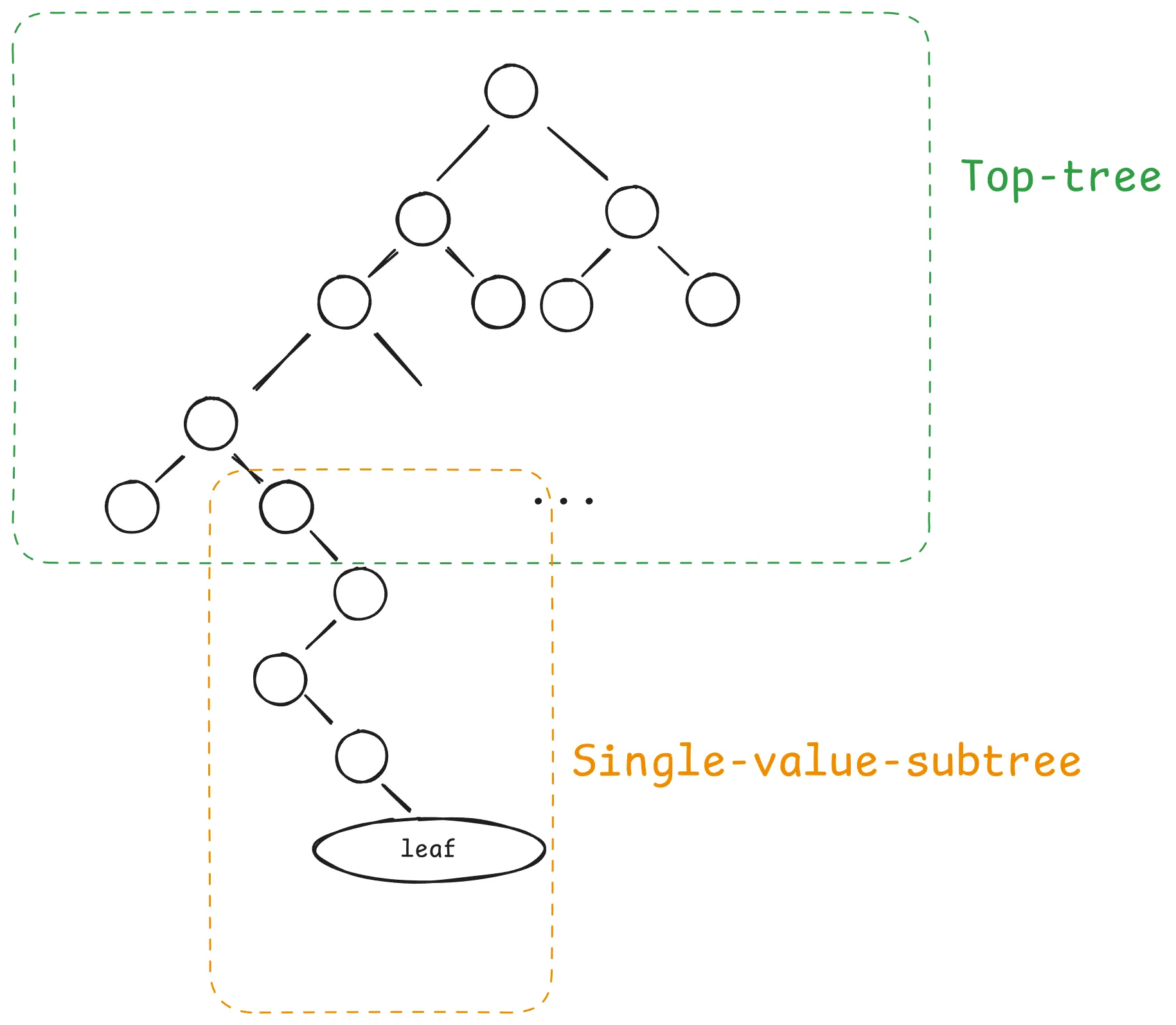
如果一个实现显式地表示这个子树，它需要大量的“虚拟”内部节点和一条长长的 H(empty, XXX) 或 H(XXX, empty) 哈希路径，这是浪费。

EL db 层中的一个简单的 实现 优化是在该子树的根处发明一个“虚拟”节点，该节点表示一个声明：“在路径 Y 处具有值 X 的空子树”。 这种实现优化消除了许多空子树的低效率，因此我们不存储它们。

请注意，在协议级别，该树仍然是 SMT。 但在实现中，我们存储节点的行为就像它们是 PMT 一样——换句话说，至少在这方面，你通过实现优化解决了通常通过规范优化（PMT）所做的事情。

覆盖 H(empty, empty) 值

在 SMT 中，你在许多级别都有 H(empty, empty)，其中 H 是用于对节点进行默克尔化的哈希函数。 这种 H(empty, empty) 计算是可缓存的，因为你可以预先计算出在所有级别发生这种情况的结果。

但是，如果我们定义 H(empty, empty) = 0，这将得到简化并降低了实现的复杂性。

所需哈希的数量呢？

SMT 中仍然有一些相当繁重的东西：我们必须做的哈希量。 给定一个到非零叶节点的​分支，我们仍然需要执行与分支长度一样多的哈希评估，对于 256 位密钥来说，这将是很多。

这在 前面提到的 Ethresearch 帖子 中得到了缓解。 我相信那里的解释非常清楚，所以我将提供一个视觉解释，可以帮助理解这个想法：

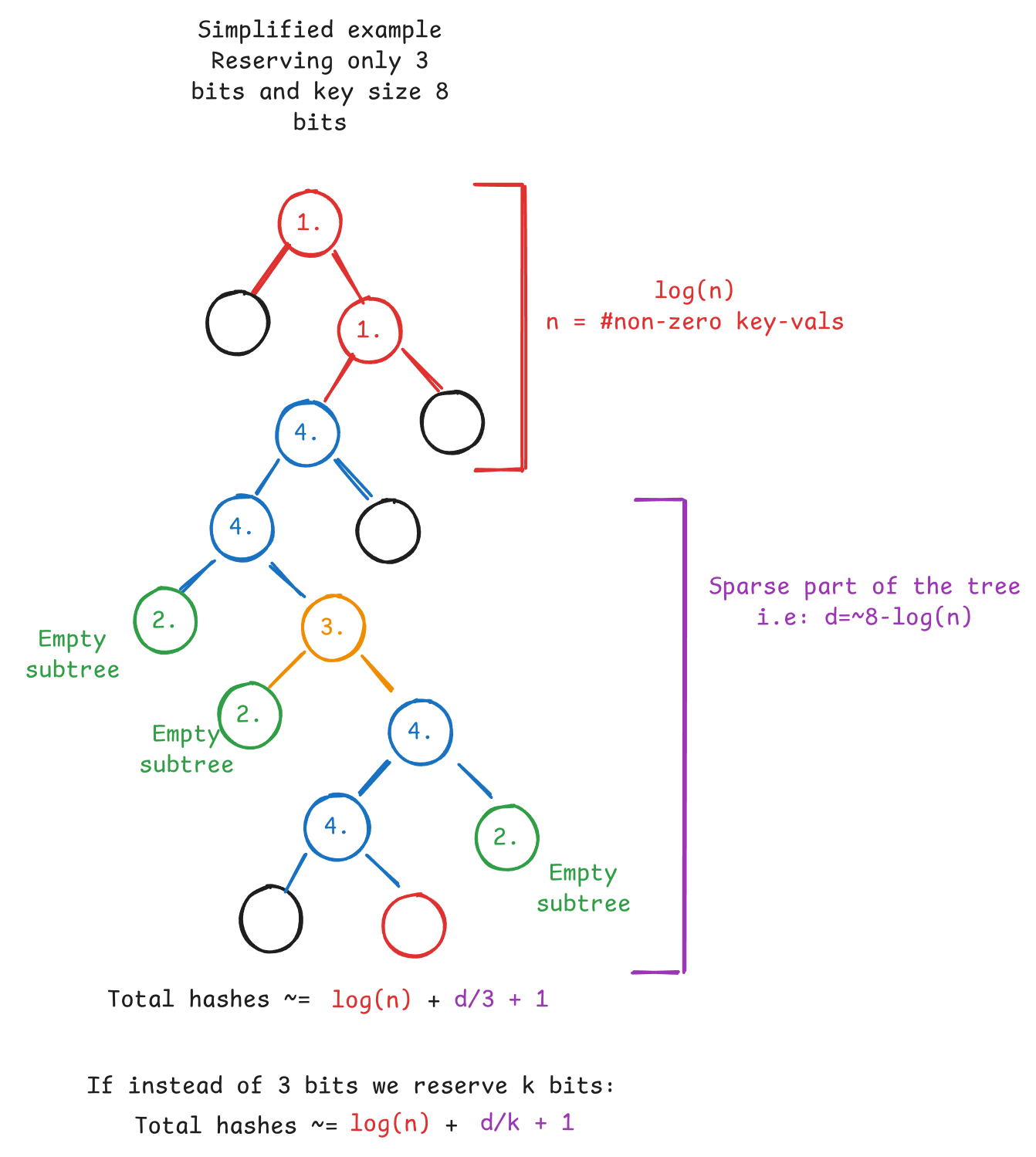
关于图片的说明：

• 节点具有在该内部节点中应用了哪个规则编号，如 Ethresearch 帖子中所述。
• 红色表示必须计算“真正的”哈希，即：“慢路径”。 其他颜色是“快路径”（即：没有哈希）。

The TL;DR is lowering the impact of extra hashing due to empty subtrees. Vitalik also notes you can tune k to reach the desired tradeoff between amortizing calculated hashes and security. Instead of requiring 16x fewer hashes in the spare part of the tree, you could require 18x (or more) fewer hashes if you accept further bits of security loss. TL;DR 是降低由于空子树导致的额外哈希的影响。 Vitalik 还指出，你可以调整 k 以在摊销计算出的哈希值和安全性之间达到所需的权衡。 如果你接受进一步的安全损失，则可以要求在树的备用部分中减少 18 倍（或更多）的哈希，而不是要求减少 16 倍的哈希。

This idea adds some complexity to the spec since we have all these extra rules on applying the hashing in the tree. Additionally, (h/t to Lev for pointing this out) this also applies to in-circuit logic, and here, “branches” are more annoying than out-of-circuit implementations. If this idea makes sense, it depends on how hard we might need to push “saving hashes” for validity proofs. 这个想法为规范增加了一些复杂性，因为我们有所有这些在树中应用哈希的额外规则。 此外，（感谢 Lev 指出这一点）这也适用于电路内逻辑，并且在这里，“分支”比电路外实现更烦人。 如果这个想法有意义，那就取决于我们可能需要多努力地推动“保存哈希”以进行有效性证明。

Note that Vitalik's very recent The Verge post includes further strategies to help on this front, e.g., using multidimensional gas to limit the number of state accesses. These ideas (and others) are orthogonal, so they could be stacked on each other. 请注意，Vitalik 最近的 The Verge 文章 包含进一步帮助解决这方面问题的策略，例如，使用多维 gas 来限制状态访问的数量。 这些想法（和其他想法）是正交的，因此它们可以相互叠加。

状态数据编码

这是许多 Verkle EIP 的想法仍然适用于二叉树的地方，使得两者共享相同的优势。 由于我不假设你了解 Verkle 的主要更改，因此我将从头开始进行解释。

让我们看看账户是如何编码到树中的：

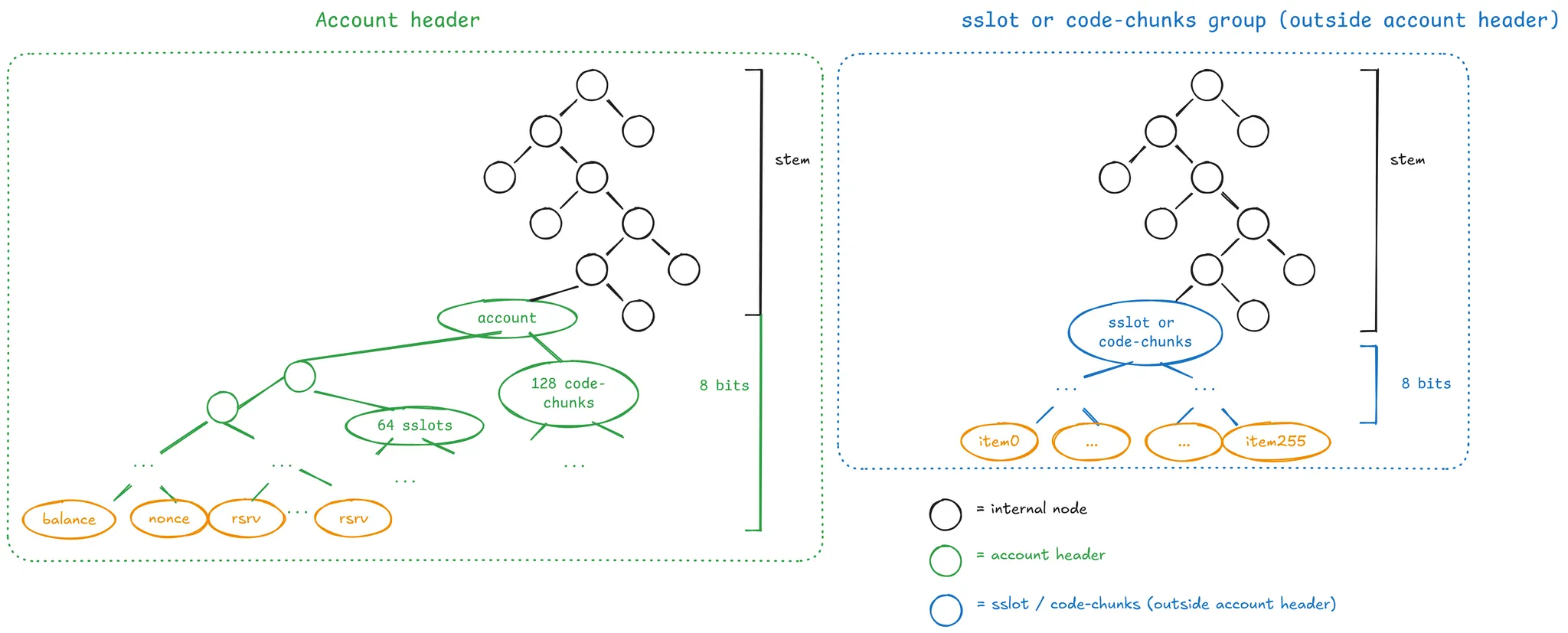
The main idea is that you address data in the tree by stem s, which are 248-bit keys that group 256 values— so each value is still referenced with a 256-bit key. The motivation is better data locality. e.g: if you need to access the nonce of an account, there’s a higher chance you will also access the balance or first bytecodes than some other random Ethereum state. If this grouping is designed properly, you can minimize the number of branches you need to prove for the data (and other db efficiency gains). 主要思想是，你通过 stem（主干/茎）s 来寻址树中的数据，stem 是将 256 个值分组的 248 位密钥——因此每个值仍然通过 256 位密钥引用。 动机是更好的数据局部性。 例如：如果你需要访问帐户的 nonce，那么你访问余额或第一个 bytecode​ 的可能性高于访问其他一些随机的以太坊状态。 如果这种分组设计得当，你可以最大限度地减少需要证明数据的分支数量（以及其他数据库效率提升）。

The stem part of the path is shown in black nodes, i.e., internal nodes. The stem guides you through the internal nodes. After the stem, we have two types of following sub-trees (which will be explained soon), which will represent 256 32-byte values. This is why these sub-trees have the “8-bit” clarification in the image above. 路径的 stem 部分显示在黑色节点中，即内部节点。 stem 会引导你通过内部节点。 在 stem 之后，我们有两种类型的后续子树（稍后将进行解释），它们将表示 256 个 32 字节的值。 这就是为什么以上图像中的这些子树具有“8 位”的澄清说明。

Note 1: the number of stems in Verkle Trees is the same in Binary Trees, thus why the main logic around the new gas costs is ~equivalent (i.e: EIP-4762 main ideas would be kept). 注意 1： Verkle 树中的 stem 数量与二叉树中的数量相同，因此围绕新的 gas 成本的主要逻辑是 ~ 等效的（即：EIP-4762 的主要思想将保留）。

Note 2: Although EIP-3102 intended to have a single tree, the storage slots have their tree “hanging” next to the account data, which makes the depth more unpredictable. The proposal now has a single tree but is balanced since storage/code chunks are spread over the tree (i.e., the same as Verkle). 注意 2： 虽然 EIP-3102 旨在拥有单个树，但存储槽的树 “悬挂”在帐户数据旁边，这使得深度更不可预测。 该提案现在具有单个树，但由于存储/代码块分布在树上，因此是平衡的（即，与 Verkle 相同）。

There are two kinds of sub-trees, which I describe in two different dotted-square colors in the image. Note these are just semantics; the tree is a ~balanced binary tree. 有两种子树，我在图像中用两种不同的虚线正方形颜色描述。 请注意，这些只是语义上的； 该树是一个 ~ 平衡的二叉树。

Account header (green)

帐户头（绿色）

The Account header describes a stem that refers to 256 values, which include: 帐户头 描述了一个 stem，它引用了 256 个值，其中包括：

• Account data: nonce, balance, code size, code hash, and some reserved ( rsrv) slots.
• The first 64 storage slot values (if the account is a contract)
• The first 128 code chunks (if the account is a contract).
• 帐户数据：nonce、余额、代码大小、代码哈希 以及一些保留的（rsrv）槽。
• 前 64 个存储槽值（如果帐户是合约）
• 前 128 个代码块（如果帐户是合约）。

Reiterating the motivation, if you access account data, there’s a high chance you’ll access other account data; thus, we put them in the same stem (i.e. branch). 重申一下动机，如果你访问帐户数据，那么你很有可能会访问其他帐户数据； 因此，我们将它们放在同一个 stem（即分支）中。

Other storage slots (blue)

其他存储槽（蓝色）

An account can use many more storage slots than the first 64 ones, so we have to put them somewhere. There’s a map that would keep grouping 256 storage slots in a stem (i.e. now different from the account stem). 一个帐户可以使用比前 64 个更多的存储槽，因此我们必须将它们放在某个地方。 有一个映射会将 256 个存储槽分组在一个 stem 中（即，现在与帐户 stem 不同）。

Other code chunks (blue)

其他代码块（蓝色）

Recall that in Verkle or Binary, we need to include the account’s code in the tree. This is done through chunkification which is “just” chunking the code and storing it in 32-byte values. 回想一下，在 Verkle 或二叉树中，我们需要将帐户的代码包含在树中。 这是通过 chunkification 完成的，它“只是”将代码分块并将其存储在 32 字节的值中。

As mentioned before, the first 128 code chunks are in the account stem, so it’s very easy/cheap to access them since you’ll need them to execute contracts.If the contract has more than 128 code chunks, those will be grouped in groups of size 256 and live in different stems in the binary tree. 如前所述，前 128 个代码块位于帐户 stem 中，因此访问它们非常容易/便宜，因为你需要它们来执行合约。如果合约有超过 128 个代码块，这些代码块将以 256 个大小的组分组，并位于二叉树中不同的 stem 中。

哈希函数

We’d like a hash function that: 我们想要一个哈希函数，它：

1. Is fast enough out-of-circuit in a CPU (i.e. for EL clients to execute)

2. It has an efficient arithmetization under a proving system that is fast enough for worst-case blocks.

3. It’s secure.

4. 在 CPU 中电路外（即，供 EL 客户端执行）足够快

5. 在证明系统下具有有效的算术化，该证明系统对于最坏情况的块来说足够快。

6. 它是安全的。

The following hash functions seem to be the candidates: 以下哈希函数似乎是候选者：

• Poseidon2
• SHA256/Blake3
• Ajtai

Each option requires proper evaluation for the points a), b), and c). Impressive progress is happening under different proving systems for some of these hash functions, and this is quite relevant for the decision. Which hash function is used shouldn’t impact (most of) the rest of the protocol changes required for Binary Trees (see next sub-section). 每个选项都需要对 a)、b) 和 c) 点进行适当的评估。 对于其中一些哈希函数，在不同的证明系统下正在发生令人印象深刻的进展，这与该决定非常相关。 使用哪个哈希函数不应影响（大多数）二叉树所需的其余协议更改（请参见下一小节）。

Note that if we end up applying the optimization explained in “ What about the number of required hashes?”, this is the hash function referred to as the “base” one. 请注意，如果我们最终应用了在“ 所需哈希的数量呢？” 中解释的优化，则这是被称为“基本”的哈希函数。

How do we encode 32-byte leaf values in finite fields?

我们如何在有限域中编码 32 字节的​叶子值？

This question makes sense if we use an arithmetic hash function such as Poseidon2 since the input of the hash function are finite field elements. The state tree stores 32-byte values. Depending on which hash function we choose, we might need to clarify how this would work under a specific field. 如果我们使用算术哈希函数（例如 Poseidon2），这个问题才有意义，因为哈希函数的输入是有限域元素。 状态树存储 32 字节的值。 根据我们选择的哈希函数，我们可能需要澄清这在特定字段下如何工作。

As an example, if we use a proving system that relies on the Mersene31 finite field, the size is 31 bits, so we can’t store 256 bits in a single 31-bit value. The minimum amount of required field elements would be nine. If this unaligned encoding is inconvenient, we can also do 24-bit encoding in 11 finite field elements. Another thing that can influence this decision, is which is the rate we need for hashing internal nodes as a consequence of the number of squeezed finite fields for whatever concluded security levels. In any case, the general idea is the same. 例如，如果我们使用依赖于 Mersene31 有限域的证明系统，则大小为 31 位，因此我们无法在单个 31 位值中存储 256 位。 所需的最小字段元素数量将是九个。 如果这种 未对齐 的编码不方便，我们也可以在 11 个有限域元素中进行 24 位编码。 另一个可能影响此决定的因素是，由于针对任何已确定的安全级别挤压的有限域数量，我们需要什么 rate 来对内部节点进行哈希处理。 无论如何，总体思路是相同的。

树序列化

Let’s analyze how the tree can be serialized and saved on disk. Since the tree's arity is two, it could be argued that it has a high overhead. 让我们分析一下树如何序列化并保存在磁盘上。 由于树的元数为 2，因此可以说它具有很高的开销。

As mentioned before, we can abstractly imagine a binary tree as: 如前所述，我们可以抽象地将二叉树想象为：

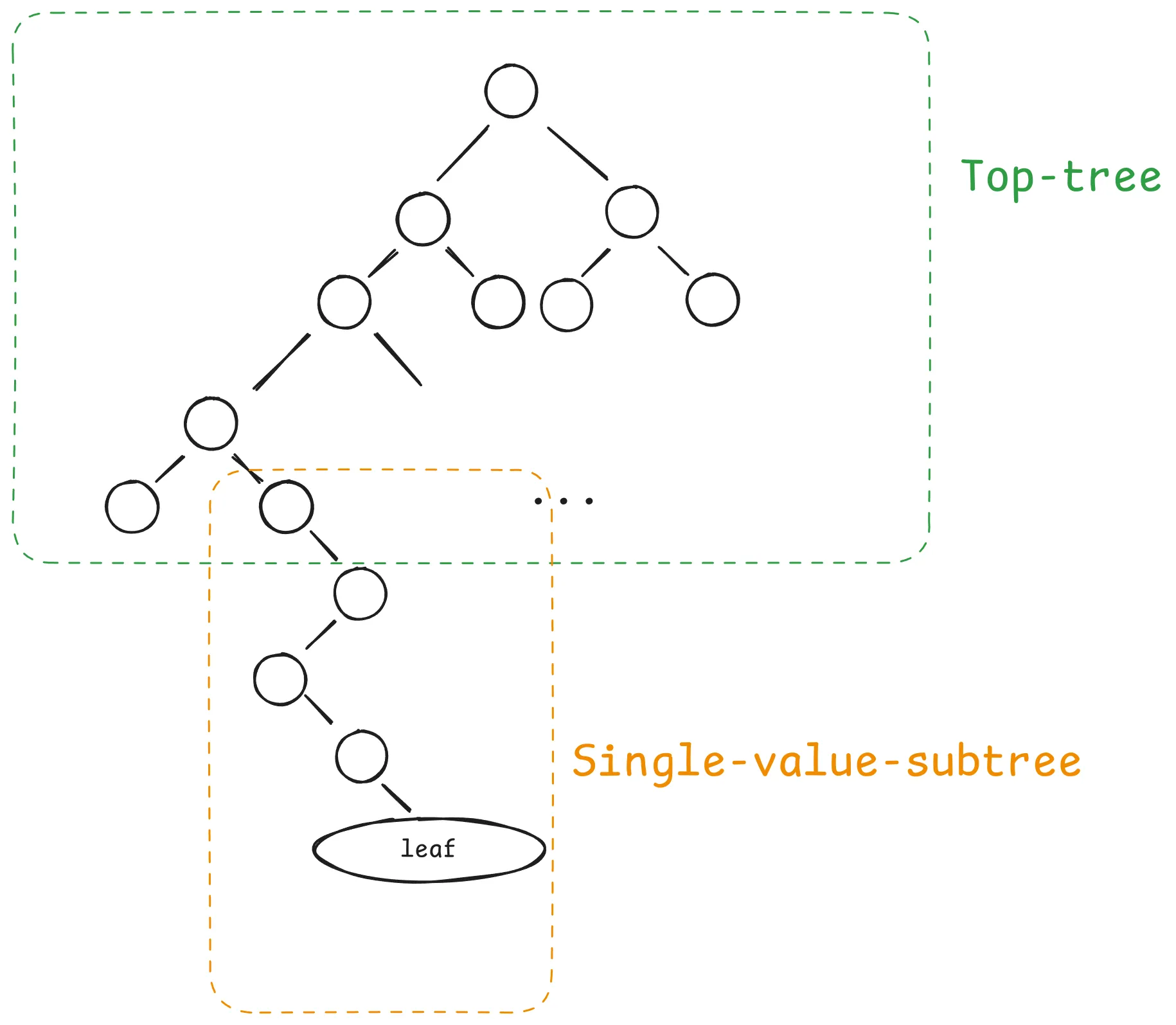
Two main parts of the tree: 树的两个主要部分：

• Top-tree refers to the tree's top part containing internal nodes containing subtrees with more than one value.
• Single-value-subtree: refers to the bottom part of the tree where we have subtrees with only one non-zero value.
• Top-tree 指的是树的顶部，其中包含包含具有多个值的子树的内部节点。
• Single-value-subtree：指的是树的底部，其中我们有只有一个非零值的子树。

The diagram corresponds to an SMT since you end up with a subtree with a single key value after some levels of internal nodes. 该图对应于 SMT，因为在某些级别的内部节点之后，你最终会得到一个具有单个键值的子树。

In the case of an SMT, optimizing the serialization of the s ingle-value subtree was already explained in a previous section. We don’t need any “optimization” for PMT since this sub-tree is already compressed in a node type. 在 SMT 的情况下，优化 s ingle-value subtree 的序列化已经在上一节中解释过了。 我们不需要对 PMT 进行任何“优化”，因为此子树已压缩为节点类型。

Regarding the Top-tree, we can note the following comment in EIP-3102: 关于 Top-tree，我们可以注意到 EIP-3102 中的以下注释：

The ethereum tree was originally hexary because this would reduce the number of database reads (eg. 6 instead of 24 in the above example). It is now understood that this reasoning was flawed, because nodes can still “pretend” that a binary tree is a hexary (or even 256-ary) tree at the database layer (eg. see https://ethresear.ch/t/optimizing-sparse-merkle-trees/3751), and thereby get the best-of-both-worlds of having the low proof sizes of the tree being binary from a hash-structure perspective and at the same time a much more efficient representation in the database. 以太坊树最初是十六叉树，因为这会减少数据库读取次数（例如，在上例中为 6 次而不是 24 次）。 现在人们已经认识到，这种推理是有缺陷的，因为节点仍然可以“假装”二叉树是数据库层中的十六叉树（甚至是 256 叉树）（例如，请参见 https://ethresear.ch/t/optimizing-sparse-merkle-trees/3751），从而获得两全其美的结果：从哈希结构的角度来看，树具有较低的证明大小，同时在数据库中具有更高效的表示形式。

To help visualize the trick, we can now imagine the tree in this way: 为了帮助可视化这个技巧，我们现在可以这样想象这棵树：

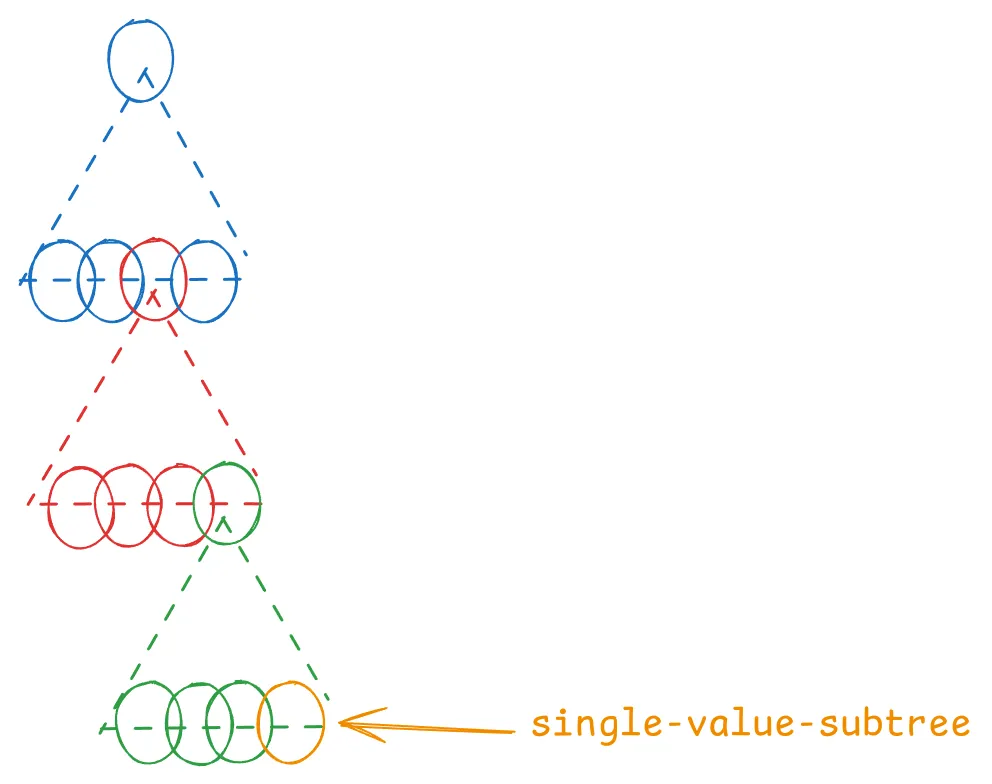
This changes the perspective of looking at internal nodes as a 4-arity tree. Each colored triangle is a single entry in the database. For example, the first blue triangle is a single entry in the database with the hash values of the Blue-Blue-Red-Blue nodes. With this single db-lookup, you can load this whole subtree, which stores an N-arity tree (in this case, 4). 这改变了将内部节点视为 4 元树的视角。 每个彩色三角形都是数据库中的单个条目。 例如，第一个蓝色三角形是数据库中的一个条目，其中包含 Blue-Blue-Red-Blue 节点的哈希值。 通过这个单一的数据库查找，你可以加载整个子树，该子树存储一个 N 元树（在本例中为 4）。

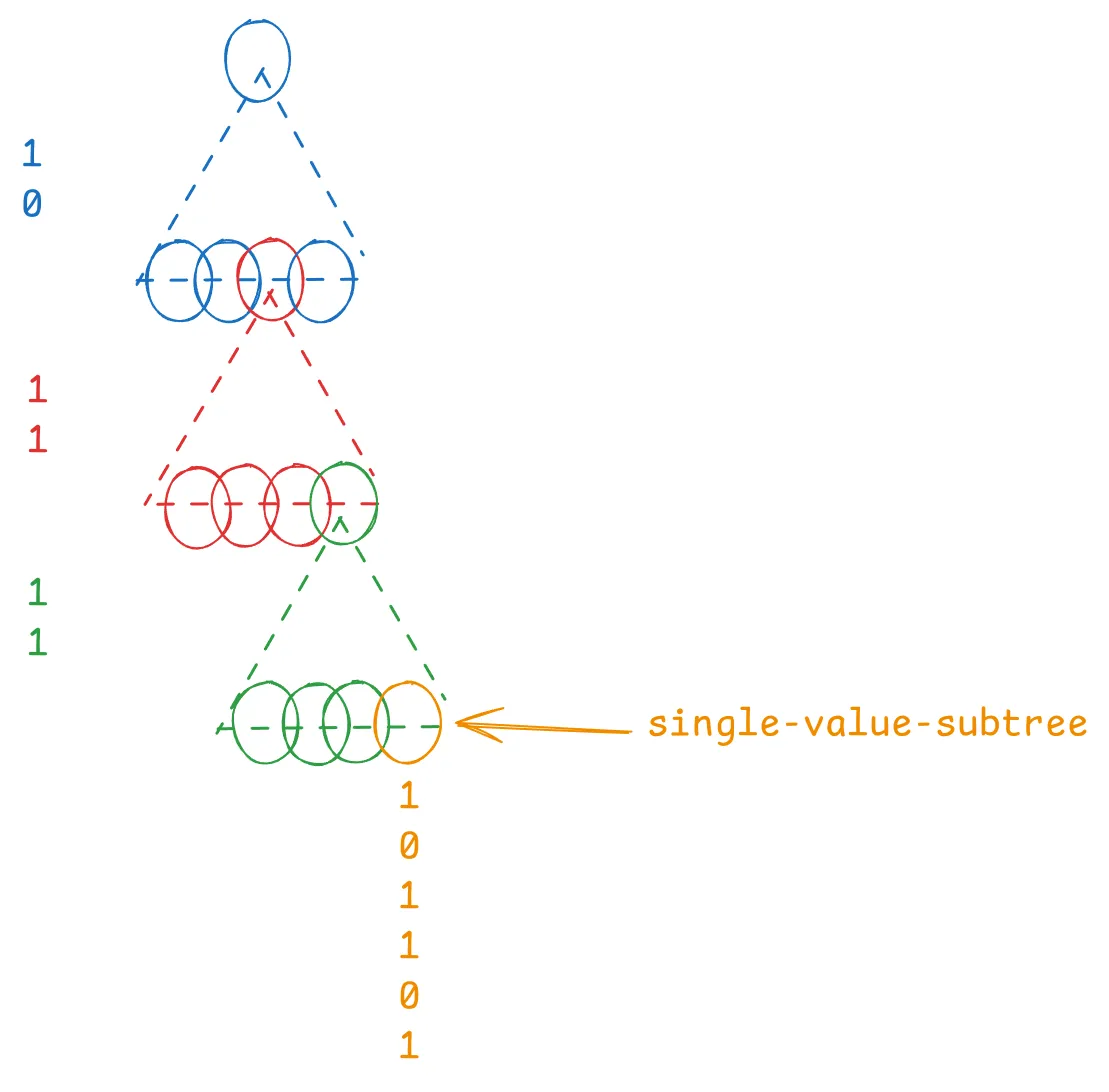
To load the path: Blue(10)Red(11)Green(11)Yellow(101101), we only do four disk lookups, compared to the naive serialization of one lookup per bit. 要加载路径：Blue(10)Red(11)Green(11)Yellow(101101)，我们只需要进行四次磁盘查找，而对于每个比特位一次查找的简单序列化，则需要更多次。

The only catch is that you need to do more hashing when loading the tree to memory to reconstruct the internal triangle node values, but this is a tunable knob that should account for the following: 唯一 的问题是，在将树加载到内存中以重建内部三角形节点值时，你需要进行更多的哈希处理，但这是一个可调的旋钮，应考虑以下因素：

• Optimal number of bottom-level subtrees (i.e: Blue-Blue-Red-Node) nodes to fit in a disk page.

• How fast is the cryptographic hash function used in the tree. This accounts for the overhead of hashing on the fly when loading the tree. Note that the trick described in the previous Cryptography hash section helps with this.

• How fast is a disk lookup.

• 适合磁盘页面的最佳底层子树（即：Blue-Blue-Red-Node）节点数。

• 树中使用的加密哈希函数有多快。 这说明了加载树时动态哈希的开销。 请注意，前面 加密哈希 部分中描述的技巧对此有所帮助。

• 磁盘查找的速度有多快。

Increasing the arity means less disk space (ROI decreases fast), fewer lookups, and more CPU work. Decreasing arity means more disk lookups, more disk usage, and less CPU work. If we use 8-bits, this would mean 256-arity which is analogous to Verkle Trees. 增加元数意味着更少的磁盘空间（投资回报率快速下降）、更少的查找和更多的 CPU 工作。 减少元数意味着更多的磁盘查找、更多的磁盘使用和更少的 CPU 工作。 如果我们使用 8 位，则意味着 256 元数，类似于 Verkle 树。

Extra optimization: Note that these X-arity subtrees reconstruction (i.e., hashing recalculation) has two parallelizable dimensions: each subtree level and between subtrees. Regarding the latter, you can overlap hashing recalculation while doing further db lookups for lower subtrees. 额外优化： 请注意，这些 X 元子树重建（即哈希重新计算）有两个可并行化的维度：每个子树级别和子树之间。 关于后者，你可以在对较低子树执行进一步的数据库查找时重叠哈希重新计算。

Note that everything described here is independent of the protocol spec. Each EL client can choose whatever tradeoff (e.g. small/big arity) makes sense for their architecture, underlying key-value database used, etc. 请注意，此处描述的所有内容都独立于协议规范。 每个 EL 客户端都可以选择适合其架构、使用的底层键值数据库等的任何权衡（例如，小/大元数）。

Important note: This is napkin math showing a tradeoff space between storage overhead and CPU workload. It would be useful to implement it and have real numbers—I’m just (re) explaining the overall idea. 重要提示： 这是餐巾纸上的数学，显示了存储开销和 CPU 工作负载之间的权衡空间。 实施它并获得真实数据将非常有用——我只是（重新）解释总体思路。

示例案例

Let's analyze the following case: 让我们分析以下案例：

• Hash function output is 32 bytes.

• For storage optimizations, use 256-arity to apply the trick.

• The tree has 2^32 non-zero key values; this should be ~4x more than expected for current mainnet data.

• 哈希函数输出为 32 字节。

• 为了进行存储优化，请使用 256 元数来应用该技巧。

• 该树有 2^32 个非零键值； 这应该比当前主网数据预期的大约 4 倍。

Let’s run some numbers: 让我们运行一些数字：

• The “top tree” has ~32 levels, and since we apply the 256-arity trick, this means we need 4 “triangles”.
• Thus, to load a leaf value, we need 4+1 disk lookups:
  • The first four lookups each load 256*32=8KiB
  • The last lookup should be ~256*3264 bytes (i.e: prefix bits + 256 32-byte values).
• If we need to reconstruct all the hashes in the path to this leaf node:
  • For an SMT: 4*(2^8-1) + (256-32) = 1244 hashes
  • If we use the trick described in the What about the number of required hashes? section, we can divide (256-32) by ~16 (or more depending on the decided collision security tradeoff).
  • For a PMT: 4*(2^8-1) = 1020 hashes
• Recall that:
  • As mentioned in the Tree serialization section, many of these hashing are parallelizable.
  • These are numbers for a single leaf-value reconstruction. In real blocks, at least one “top triangle” is shared.
  • Despite parallelizability or top-triangle sharing, the amount of hashing could be significant, but the (out of circuit) performance hit depends on the chosen hash function and aritry-number trick.
• The total tree size would be (

28+…+

232)*32~=128GiB, half the size of the naive serialization (~

233 nodes * 32 bytes = 256GiB). Note this is an estimation to know the order of magnitude.

• “顶层树”有约 32 层，由于我们应用了 256 元数的技巧，这意味着我们需要 4 个“三角形”。
• 因此，要加载叶子值，我们需要 4+1 次磁盘查找：
  • 前四次查找每次加载 256*32=8KiB
  • 最后一次查找应为约 256*3264 字节（即：前缀位 + 256 个 32 字节的值）。
• 如果我们需要重建到此叶子节点路径中的所有哈希值：
  • 对于 SMT：4*(2^8-1) + (256-32) = 1244 个哈希值
  • 如果我们使用 所需哈希的数量呢？ 部分中描述的技巧，我们可以将 (256-32) 除以约 16（或更多，取决于已确定的冲突安全性权衡）。
  • 对于 PMT：4*(2^8-1) = 1020 个哈希值
• 回想一下：
  • 正如 树序列化 部分中提到的，这些哈希值中的许多都是可并行化的。
  • 这些是单个叶子值重建的数字。 在真实区块中，至少共享一个“顶层三角形”。
  • 尽管具有可并行性或顶层三角形共享，但哈希的数量可能很大，但是（电路外）的性能损失取决于所选的哈希函数和位元数技巧。
• 树的总大小将为 (

28+…+

232)*32~=128GiB，是简单序列化的一半大小(约

233 个节点 * 32 字节 = 256GiB)。 请注意，这是一个估计值，用于了解数量级。

这是一个估计值，现实生活中的实现可能更加棘手，因此请谨慎对待。

附录

This section describes some lateral topics regarding Binary Trees. 本节介绍了一些关于二叉树的横向主题。

How much of the current Verkle progress is reusable for Binary Trees?

当前 Verkle 进展中有多少可以重用于二叉树？

Here are the current EIPs that are related to Verkle: 以下是与 Verkle 相关的当前 EIP：

• EIP-6800 describes the switch to the new tree and how data is stored there.

• EIP-4762: describes the gas cost changes, which now penalized big witnesses.

• EIP-7748: describes how the state conversion would work.

• EIP-7709: describes how BLOCKHASH would now use data saved in EIP-2935.

• EIP-6800 描述了切换到新树以及如何在其中存储数据。

• EIP-4762：描述了 gas 成本变化，该变化现在惩罚大型见证。

• EIP-7748：描述了状态转换的工作方式。

• EIP-7709：描述了 BLOCKHASH 现在将如何使用保存在 EIP-2935 中的数据。

If we guide ourselves on what changed by the mentioned EIPs we can say: 如果我们根据上述 EIP 中更改的内容进行指导，我们可以说：

• EIP-6800 would be partially reused, mainly regarding data encoding into the tree.

• EIP-4762 for the gas model would be similar since the main goal is penalizing witness costs.

• BLOCKHASH resolving from system contract storage (EIP-7709) doesn’t depend on the target tree — so it’s the same.

• State conversion (EIP-7748) would be the same since nothing about the current Overlay Tree migration strategy depends on the shape of the target tree.

• The pre-images distribution sub-problem of the state conversion is the same since those preimages depend on the current tree (MPT), not the target tree.

• The Verkle cryptography stack, which includes Bandersnatch (+Banderwagon), Multiproof + IPA, and Pedersen Hashes, would be dropped. For binary trees, we’d be including validity proof of the pre-state (and post-state updates).

• The current ~200 execution-spec-test test vectors we’ve been working on for Verkle could be adjusted with low effort. The same applies to state-conversion test vectors (which don’t exist yet).

• EIP-6800 将被部分重用，主要涉及将数据编码到树中。

• EIP-4762 的 gas 模型将类似，因为主要目标是惩罚见证成本。

• 从系统合约存储解析 BLOCKHASH (EIP-7709) 不依赖于目标树 — 因此它是相同的。

• 状态转换 (EIP-7748) 将是相同的，因为当前 Overlay Tree 迁移策略没有任何内容依赖于目标树的形状。

• 状态转换的预映像分布子问题是相同的，因为这些预映像依赖于当前树 (MPT)，而不是目标树。

• Verkle 密码学堆栈，包括 Bandersnatch (+Banderwagon)、Multiproof + IPA 和 Pedersen 哈希，将被删除。 对于二叉树，我们将包括预状态（和后状态更新）的有效性证明。

• 我们一直在为 Verkle 工作的当前约 200 个 execution-spec-test 测试向量可以通过较低的成本进行调整。 同样适用于状态转换测试向量（尚不存在）。

Note that EIP-7736, proposing leaf-level state expiry, could also be applied to Binary Trees. 请注意，EIP-7736 提出叶级状态过期，也可以应用于二叉树。

“Normal” State proofs

“正常”状态证明

Note that for L1, we’ve always used a proving system to prove the pre-state for block execution. This won’t be explained since it still isn’t clear if STARKs, GKR, or another strategy will be used. Still, simple proofs can be useful, as mentioned in Use cases of witnesses other than verifying blocks in Vitalik’s article. 请注意，对于 L1，我们一直使用证明系统来证明用于区块执行的预状态。 这不会被解释，因为它仍然不清楚是否会使用 STARK、GKR 或另一种策略。 尽管如此，简单的证明可能是有用的，正如 Vitalik 的文章 中 验证区块以外的见证用例 中提到的。

A way to visually see an option on how to do it in a SMT: 一种以可视方式查看如何在 SMT 中执行此操作的选项的方法：

![image](https://img.learnblockchain.cn/2025/05/04/ByTXu_fbye.png

• 原文链接： hackmd.io/@jsign/binary-...
• 登链社区 AI 助手，为大家转译优秀英文文章，如有翻译不通的地方，还请包涵～