Orbit/Vorbit SSF 中的巩固激励 - 权益证明 / 经济学
- 以太坊中文
- 发布于 2025-01-27 13:50
- 阅读 899
本文深入探讨了在Orbit SSF(Solo Staking Friendly Validator Set Management)框架下,如何设计有效的巩固激励机制,以平衡验证者规模、活跃度和收益之间的关系。提出了一个系统性的框架,该框架由两个形状变量f_1和f_2以及一个尺度变量f_y组成,通过调整这些变量来优化验证者集合的巩固程度,同时兼顾公平性和经济安全。
1. 介绍
1.1 背景
Orbit SSF 的一个关键主张是,验证者基于规模进行轮换,因此那些拥有较大余额的验证者会更频繁地处于活跃状态,同时仍然让所有验证者获得大致相等的收益。活跃的验证者可能会被罚没(slashed),因此大型验证者将比小型验证者承担更大的风险。撇开大规模罚没事件不谈,Staking 池可能更倾向于运行较小的验证者,以便及早发现错误的设置,并且只影响其总权益的一小部分。然而,如果 Staker 能够在可能的情况下进行合并,这是非常可取的——在其他条件相同的情况下,合并程度将直接影响协议能够提供的经济安全性。因此,Orbit SSF 应该提供个人合并激励。这些可以与集体合并激励相结合,后者在合并时使每个人都平等地受益。
收益应该如何随验证者规模和活跃率变化,尚未得到详尽的调查。Orbit SSF 的文章提供了一个良好的起点,但进行彻底的审查将非常有价值。事先可能也很难知道如何分配激励,使得它们不会偏袒某些特定规模的验证者,从而导致验证者聚集在特定的规模。因此,一种用于自动化和调整分配的机制可能是可取的。此外,Vorbit SSF 提出了验证者规模和活跃率之间的一种不太线性的关系,这更有力地支持了在设计激励时同时考虑这两者。
另一个问题是,合并激励的幅度应该如何随合并程度和 Staking 收益变化,以及应该如何量化合并。这既关系到总激励的形状,也关系到总激励的规模。这里的一个问题是,协议不知道 MEV 的水平,而提议权仍然应该像今天一样根据权益分配。另一个需要进一步研究的问题是,激励应该在哪个合并程度下变为零。
1.2 概述
本文分析了如何设计合并激励以匹配协议需求,提供了一个系统的框架。该框架由两个 0-1 范围内的形状变量 f_1 和 f_2 以及一个标度变量 f_y 组成。合并力 f_1 随合并程度变化,合并程度根据给定 Staking 存款规模 D 时的验证者数量 V 计算得出。它在第 2 节中介绍。第 3 节然后探讨了力分配 f_2,它根据每个验证者的活动率 a 为其提供个人合并激励,可能还依赖于它们的大小 s。这些变量进行标度,以通过与合并力标度 f_y 相乘来实施对收益的调整,这在第 4 节中描述。关注内生变量,衰减的集体激励可以参数化为
f_1f_y
而衰减的个人激励可以参数化为
f_1f_2f_y.
如果 f_1 和 f_y 对于两种激励都保持相同(一个现实的设计目标),则衰减的合并激励 y_c 的完整方程变为
y_c = f_1f_y(c+f_2),
其中 c 是集体激励的相对强度。当包括先前概述的外生变量时,活动率为 a_v 且大小为 s_v 的验证者 v 的合并激励 y_c(v) 变为
y_c(v) = f_1(V!, D)f_y(y')(c+f_2(a_v, s_v)),
其中 y' 反映了捕获 Staking 收益的某种度量,可能包括 MEV 的估计值(第 4 节提出了几种变体)。第 5 节考察了激励的衰减、提升和发行中性模式,其中衰减和发行中性模式被强调为最有趣的。衰减模式用作本文中的主要示例,通过该模式,y_c 通过 y'_i=y_i-y_c 更新每个验证者的目标发行收益。第 6 节提供了基于该分析的最终规范。
附录 A 介绍了在 Staker 余额的齐普夫分布下的验证者数量的近似值,附录 B 提供了本文与 Orbit SSF 文章中激励设计的详细比较。附录 C 提供了用于生成具有逐渐变化的齐普夫性的验证者集的方程,这些方程在模拟合并的影响时很有用。
2. 合并力 f_1
合并力 f_1 对于所有验证者都是相同的,并且随合并程度变化,具体而言,随验证者数量 V 和权益存款规模 D 变化,即 f_1(V!,D)。当被采用为衰减激励时,它在合并不良的情况下接近 1,而在合并良好的情况下接近 0,如果用作提升激励,则情况相反(即 1-f_1)。第 2.1 节首先根据 Staker 的齐普夫分布,提供了对合并何时符合预期的简单近似。第 2.2 节然后探讨了 f_1 的适当形状,第 2.3 节概述了动态 f_1 的优点和缺点。
2.1 齐普夫 Staker 数量下的近似验证者
将合并力与数据集合并程度的某些有形度量联系起来似乎是合理的。早期假设是,以太坊可以希望吸引资本按照 齐普夫定律 分布的 Staker。一旦数据集达到了相应的合并程度,进一步合并的激励应该可以论证地 非常小。Vorbit SSF 文章提出了 两个方程,可用于计算在 Staker 余额的齐普夫分布下的验证者数量 V_Z。然而,这些方程相当复杂,并且不太适合作为协议规范的一部分。
因此,本文的附录 A 推导了三个简化的方程,图 A1-A2 详细说明了它们的准确性。由于其简单性和相对准确性,本文将使用对数调整的近似
V_Z = \frac{D}{20\,\ln D}。
给定特定的权益存款规模 D,因此可以轻松计算在 Staker 余额的齐普夫分布下的验证者数量。
2.2 合并力形状
现在将定义 f_1 曲线的潜在形状。理论上的最大验证者数量是 V_{\text{max}}=\lfloor D/s_{\text{min}}\rfloor,其中 s_{\text{min}} 是 32 的最小验证者规模。理论上的最小验证者数量是 V_{\text{min}}=\lceil D/s_{\text{max}}\rceil,其中 s_{\text{max}} 是 2048 的最大验证者规模。可以注意到,s_{\text{max}} 和 s_{\text{min}} 的设置因此会影响输出。
2.2.1 线性形状
一个示例是随着验证者数量的减少(合并的增加)线性地减小合并力。给定一个起点 V_{\text{start}},形成这种线性 f_1 的方程是:
f_1 = \frac{V-V_{\text{start}}}{V_{\text{max}}-V_{\text{start}}}。
图 1 显示了四个依赖于此方程的示例。最简单的是通过设置 V_{\text{start}}=V_{\text{min}} (黑线)或通过设置 V_{\text{start}}=V_Z (红线)将 f_1 扩展到整个范围。另一种选择是让 f_1 通过 V_{\text{start}} = (V_{\text{min}}+V_Z)/2 (黑色虚线)在 V_Z 和 V_{\text{min}} 之间的中点达到 0。第四个选择是在 V_Z 处强制执行一些特定的 f_1,此处表示为 f_z,通过方程
V_{\text{start}}=\frac{V_Z-f_zV_{\text{max}}}{1-f_z}。
在该图中,f_z 设置为 0.05 (红色虚线)。此选项的好处是可以更精确地了解在齐普夫合并程度下剩余的激励,而第一个选项(在较小程度上还有第三个选项)将看到 f_z 在 D 上略有漂移(与附录 A 中 f_1 的线性近似值进行比较)。原因是让激励比在 V_{\text{min}} 更早达到 0,此处是通过依赖 V_Z,是为了在足够的合并程度下促进小型验证者的公平性。避免将 f_1=0 设置得像 V_Z 一样高的一个潜在原因是,如果许多 Staker 只有在从中获得更高的收益时才会合并,那么它会排除在 V_Z 处达到平衡的可能性,这可能是一个合理的假设(更多内容见下文)。
先前已经探讨了相对于活动权益比例 D_a/D 呈线性的激励。附录 B 提供了与该策略的比较。线性对于集体合并激励特别有吸引力,其中曲线的导数表示激励。Staker 从 f_1 的减少中 获益,但其大小本身不会影响合并的激励。
图 1. 线性合并力 f_1 的四个示例,在不同的验证者数量处达到零。
2.2.2 Sigmoidal(S形)形状
一个更通用的替代方案从先前所述的第一步开始:
x = \frac{V-V_{\text{start}}}{V_{\text{max}}-V_{\text{start}}}。
然后应用第二步来产生 S 形曲线:
f_1 =\frac{1}{\displaystyle 1 + \Bigl({\frac{1 - x}{tx}}\Bigr)^{2}}。
参数 t 控制 S 形曲线的主要过渡发生的位置,而幂(此处为 2)调整其陡峭度。图 2 说明了一个 S 形曲线(幂为 2),它通过设置 t=5 将过渡推到左侧,接近 V_Z。起点设置为 V_{\text{start}} = (V_{\text{min}}+V_Z)/2 (如先前图 1 的黑色虚线曲线中所示)。
图 2. 具有 S 形形状的合并力,它具有可调节的陡峭度和过渡点。
对于个人激励,更重要的是考虑陡峭的 S 形合并力,其中 f_1 的大小调节 Staker 之间的收益差异,从而表示合并激励。对于集体激励,f_1 大小的斜率反而表示合并激励。可以用于集体激励和个人激励的一种折衷方案是混合线性形状和 S 形形状。
2.2.3 混合形状
可以通过以下等式生成混合形状
f_1 =\frac{w}{\displaystyle 1 + \Bigl(\frac{1 - x}{tx}\Bigr)^{2}}+(1-w)x。
等式的第一部分创建 S 形形状,该形状由 w 对第二部分中的线性形状进行加权。图 3 显示了一个等权重 w=0.5 的示例,再次使用 t=5 和与先前相同的 V_{\text{start}} 在 V_{\text{min}} 和 V_{\text{start}} 之间的中点。请注意 400k 和 1M 验证者之间相当固定的斜率,这与线性形状相关。
图 3. 混合合并力,将线性 f_1 曲线和 S 形 f_1 曲线加权在一起。
与其他选项一样,需要考虑的一个问题是 f_1 是否应该已经在 V_Z 附近变为零,或者在整个范围内保留一些小的激励是否合理。后一个选项似乎更具吸引力,因为据推测,在均衡状态下,必须保留一些个人激励。换句话说,如果对于 Staking 服务提供商 (SSP) 来说,将个人激励设置为零在 V_Z 不会带来其他收益,那么它会排除达到这一点的可能性。但是,在 V_Z 处存在的任何剩余的集体合并激励也可以考虑在内。
2.3 固定或动态计划
合并激励可以具有固定或动态计划。在固定计划下,一些权益数量处的特定验证者组成将给出特定的 f_1,如图 1-3 所示。在动态计划下,还存在一个时间分量,并且 f_1 将缓慢调整到其规定的目标。动态计划仍然可以具有与作为目标的 f_1 曲线相同的类型,如先前在 此处 针对发行奖励曲线给出的示例,其典型的逐步变化在 此处 捕获。
最自然的选择是采用没有时间分量的固定计划。原因是 与奖励曲线的原因相同:重点是长期的影响。该曲线可以捕获公平性和合并的激励之间的理想平衡,而无需将时间作为参数。但是,如果该协议希望采取更极端的措施,例如,通过让个人激励 (f_1f_2f_y) 的 f_1 接近无穷大来强制执行齐普夫分布,那么则需要一个动态计划。但是,这种策略可能会导致小型单 Staker 和委托 Staker 在均衡状态下产生非常高的收益差异。因此,最好通过类似于本文概述的 f_1 曲线在合并的需要和公平的需要之间取得平衡。
如果特别担心 Staker 暂时改变验证者组成,例如为了响应 MEV 的变化或作为阻止其他 Staker 的一种手段,当然可以在发生转变时逐步应用对长期力的更改。除了增加复杂性之外,另一个风险是,如果 f_1 没有随着情况的变化而足够快地调整,则存在 Staker“过度调整”自然均衡合并程度的风险。
3. 个人激励的力分配 f_2
力分配 f_2 在验证者集中分配合并力,从而形成个人激励。在基线“衰减”模式下,具有特定 f_2 的验证者会收到 f_1f_2f_y 的个人收益衰减。在提升模式下,它在相同的 f_2 曲线下会收到 f_1(1-f_2)f_y 的提升,但是本节将以衰减模式为中心(第 5 节将进一步回顾模式,并在表 1 中进行比较)。最大规模的验证者通常具有 f_2=0,因此没有衰减。最小规模的验证者通常具有 f_2=1,因此会收到最大的衰减 f_1f_y。本质上,给定最大/最活跃的验证者和最小/最不活跃的验证者之间的收益差异 f_1f_y,f_2 的作用是确定对两者之间所有验证者的影响。
有两种主要途径可以计算每个个人验证者的 f_2:
- AID (第 3.1 节):基于应用的公平概念的激励差异,例如与活动率或验证者规模相关。此解决方案最容易实施。
- CID (第 3.2 节):累积激励差异作为 AID 之上的覆盖,根据验证者规模的排序列表分配设计的激励。这是一种尝试在某些验证者规模变得过于有利时调整奖励的方式,但是它更复杂。
第三个选项“BID”(第 3.3 节)尝试通过计算 AID 和 CID 来实现平衡,从而让 f_2 成为两者的加权平均值。
3.1 AID
通过 AID,协议会根据验证者承担的风险或占用的空间来调整收益。一个自然的假设是风险随 活动率 a 变化(验证者作为证明者活跃的时间比例),而活动率又随验证者规模 s 变化。如果验证者在证明可用链和终结工具时的活动率不同,但是对于验证者在证明职责之间的活动率仍然不同,则需要定义一个统一的度量。本节将回顾 f_2 曲线的四个选项:
- 第 3.1.1 节;f_2(a):根据从 a 得出的假定风险的估计值来衰减收益。
- 第 3.1.2 节;f_2(s):根据验证者的大小 s 模拟验证者费用。
- 第 3.1.3 节;f_2(a) 或 f_2(s) 或 f_2(a, s):依赖于一个在 a 或 s 或两者上具有等距减少的对数标度度量。
- 第 3.1.4 节;f_2(a, s):使用前两个选项的加权平均值。
第 3.1.5 节最后比较了这些选项并绘制了它们的图。
3.1.1 a 中的线性——关于预期活跃权益的中性
将验证者 v 的活动率定义为 a_v。一个直观的解决方案是 先前倾向于 让 f_2 通过扣除活动率来捕获不活动百分比
f_2 = 1-a_v。
可以重新调整方程,使其始终在整个范围内扩展力。将最小可能的活动率定义为 a_{\text{min}},将最大可能的活动率定义为 a_{\text{max}}。因此,可以按如下方式计算活动率为 a_v 的验证者的 f_2
f_2 = \begin{cases} \displaystyle \frac{a_{\text{max}} - a_v}{a_{\text{max}} - a_{\text{min}}} & \text{如果 } a_{\text{max}} \neq a_{\text{min}} \\[0.1ex] \\ 0 & \text{如果 } a_{\text{max}} = a_{\text{min}}。 \end{cases}
以活动为风险为重点,上述两个公式呈现的 f_2 类型线性缩放会产生以下特征:由于 Staker 专门为不活动买单,因此具有将要 Staking 的禀赋的代理——实现一些特定的预期活跃权益——无论它选择哪种确切的验证者规模分配,受到的影响都相同。例如,使用一个 2048 ETH 验证者和六十四个 32 ETH 验证者 Staking 4096 ETH 的代理将获得几乎相同的预期活跃权益,这与选择运行四个 1024 ETH 验证者时获得的预期活跃权益几乎相同,因此,其权益平均获得的 f_2 几乎相同。任何产生相同数量的活跃权益的其他组合将产生相同的平均 f_2。
以活动作为风险为重点来看,这似乎是一个自然的解决方案。活动率和验证者组成实际如何转化为风险的问题存在许多细微差别。与 Staking 服务提供商的进一步对话可以提供重要的观点和更详细的措施。
3.1.2 与 s 成反比——关于验证者数量的中性
从协议的角度来看,第 3.1.1 节中的两个示例分布实际上应该被同等对待吗?鉴于第一个选项会导致 65 个验证者,因此具有 4 个 1024 ETH 验证者的第二个选项可能看起来更好。最好能够完全完成 4096 ETH 禀赋的终结,方法是在一个Slot中仅为总共 4 个验证者提供空间,而不是需要为 65 个验证者提供空间。与验证者数量无关的方程会是什么样的?将验证者的大小定义为 s_v。那么,寻找的方程就是
f_2 = \frac{32}{s_v},
大小为 32 的验证者会收到完全衰减(f_2=1)。也可以重新调整此方程,使其始终在整个范围内扩展力:
f_2 = \frac{ s_{\text{min}} ( s_{\text{max}} - s_v ) }{ s_v ( s_{\text{max}} - s_{\text{min}} ) }。
反比例的 f_2 可以被认为是模拟经典的“ 验证者费用”,并且该机制与某些特定禀赋分布到的验证者数量无关。由于构造合并力的方式是从收益中扣除,因此必须通过反比关系收取费用。如果将相同的 f_2 应用于每个验证者,那么较大的验证者将必须支付更高的名义费用,因为其总奖励更高。反向缩放通过在权益上加权来纠正了这一点。理解该方程的一种方法是考虑使用任何验证者大小 Staking 2048 ETH 的结果。那么,64 个 32 ETH 验证者的总费用是 1 个 2048 ETH 验证者的 64 倍,32 个 64 ETH 验证者的费用是 32 倍,等等(忽略重新缩放归一化)。理解它的另一种方法是,f_1f_y 规定了一个 32 ETH 验证者的验证者费用。运行一个 64 ETH 验证者的总成本与一个 32 ETH 验证者相同,因此在分配到两倍的权益时,f_1f_y 必须减半。
在 Orbit SSF 中,如果阈值为 2048 ETH,则 a_v 和 s_v 将呈线性相关,那么该方程也很容易根据 a_v 来构造:
f_2 = \begin{cases} \displaystyle \frac{ a_{\text{min}} (a_{\text{max}} - a_v) }{ a_v (a_{\text{max}} - a_{\text{min}}) } & \text{如果 } a_{\text{max}} \neq a_{\text{min}} \\[0.1ex] \\ 0 & \text{如果 } a_{\text{max}} = a_{\text{min}}。 \end{cases}
但是,如果在例如 1024 处进行阈值处理,或者在 Vorbit SSF 中,验证者规模和活动率之间存在更详细的联系,这将不起作用,如该文章的 图 22 所示。
3.1.3 对数标度——对数域中的等距 f_2
虽然在 s_v 上进行反比例缩放可能会导致较小的验证者集,但与 a_v 上的线性构造相比,它可能显得不那么“公平”。如果专门设计该分布来补偿更活跃的验证者,从而承担更大的风险,那么控制较少权益的代理可能会忽略其较低的收益。另一方面,也可以构造公平性来反映 Staker 给协议带来的压力。
另请注意,对于预期活跃权益而言,中性的分布(第 3.1.1 节)对于 32-128 ETH 范围内的验证者规模将给出非常相似的结果(另请参见第 3.1.5 节中的图 4)。对于验证者数量而言,中性的分布(第 3.1.2 节)对于 512-2048 ETH 范围内的验证者规模将给出非常相似的结果。对于 Staker 来说,一个折衷的分布似乎更可取,在该分布中,从对 a_v 或 s_v 进行相同的对数缩放更改都会在任何点上对 f_2 产生相同的影响。这种力分配会缩放到整个范围,为
f_2 = \frac{\log_2\left(s_{\text{max}}/s_v \right)}{\log_2\left( s_{\text{max}}/s_{\text{min}} \right)},
或
f_2 = \begin{cases} \displaystyle \frac{\log_2\left(a_{\text{max}}/a_v \right)}{\log_2\left( a_{\text{max}}/a_{\text{min}} \right)} & \text{如果 } a_{\text{max}} \neq a_{\text{min}} \\[0.1ex] \\ 0 & \text{如果 } a_{\text{max}} = a_{\text{min}}, \end{cases}
或者是两者的加权组合。该构造避免了先前两个想法的更极端的结果。
3.1.4 线性 f_2 和反向 f_2 的加权
第四个选项是将线性构造(3.1.1)与反向构造(3.1.2)加权在一起。一个好处是两者都有明确的解释,然后可以扩展到加权度量。假设 a_{\text{max}} \neq a_{\text{min}},否则 f_2=0,则方程变为
f_2 = w\frac{ a_{\text{max}} - a_v }{ a_{\text{max}} - a_{\text{min}} } + (1-w)\frac{ s_{\text{min}} ( s_{\text{max}} - s_v ) }{ s_v ( s_{\text{max}} - s_{\text{min}} ) }。
下一个小节中图 4 中显示的黄色平均值设置 w=0.5。请注意,当 a 和 s 之间的关系不那么线性时(例如 Vorbit SSF),此选项特别有用。
3.1.5 AID 构造的比较
图 4 显示了先前介绍的四个选项,它们使用在 2048(也是 s_{\text{max}})进行阈值处理的 Orbit SSF 的验证者大小和活动率,以便 a 和 s 始终呈线性相关。绿色和红色 $f_2$s 与估计的风险或占据的验证者位置无关,这给出了相当“不对称”的分布。对数缩放(蓝色)和平均(黄色)分布不太不对称(至少从对数缩放的角度来看),并且当验证者的大小增加一倍时,会对 f_2 产生大致相等的影响。
图 4. 在基线 Orbit SSF 阈值处理下绘制的力分布 f_2 的四个选项。在绿色中,一种在 a 中呈线性且对于给定禀赋的预期活跃权益呈中性的分布。在红色中,一种与 s 成反比且对于某些禀赋使用的验证者数量呈中性的分布。在黄色中,绿色和红色力分布的平均值,在蓝色中,一种对数缩放的分布。
3.2 CID
通过 AID 计算 f_2 既简单又直观,但是可以注意以下两点:
- 如果该机制不能正确地模拟风险,则验证者可能会聚集在产生最佳风险调整后奖励的规模处,并且该分配可能会过度偏离某些自然的齐普夫状态。
- 协议的优先级可能会随着合并程度而变化,在低合并的情况下侧重于 Staker 占用多少空间,并在合并程度已经良好时侧重于与风险相关的公平性。
可以通过将累积激励差异 (CID) 作为特定 AID 策略之上的覆盖来解决 (1) 和 (2) 两点。首先,定义一个中性的验证者组成,并指定此组成中适用的 AID 策略。然后,根据大小对验证者进行排序,并给出与它们在排序列表中的特定位置相关的 f_2。
一个合理的方法可能是将 验证者 的齐普夫分布定义为中性的,以便每个对数间隔的箱子的总 ETH 是固定的。请注意,这种构成比从 Staker 的齐普夫分布生成的构成要合并得少很多,在 Staker 的齐普夫分布中,每个超过 2048 ETH 的 Staker 会将其权益划分为几个大的验证者。例如,与分析 Staker 齐普夫分布的先前文章中的 图 2 进行比较。
将验证者的齐普夫分布定义为中性的,并在对数缩放的 AID 上应用 CID。具有此规范的各种验证者构成的结果显示在图 5-10 中。如图 5-6 所示,当验证者分布为齐普夫分布时,改变其规模的验证者会发现其 f_2 的变化与在纯对数缩放的 AID 下的变化一样(图 4 中的蓝线)。如果合并程度小于齐普夫分布,则 f_2 更接近反比例分布(图 4 中的红线)。如果合并程度优于齐普夫分布,则 f_2 反而更接近线性分布(图 4 中的绿线)。图 7-8 说明了后一种方案。因此,协议的优先级会随着合并程度而变化,如上文第 (2) 点所述。为了在没有执行基线 Orbit 加权的情况下更紧密地与该点保持一致,还需要在合并改善时逐渐将焦点从 s 转移到 a。可以考虑 (1-f_1)a+f_1s 或稍微更精确的东西。
图 5. 在齐普夫验证者集下绘制的力分布 f_2 与每个箱子的验证者数量的关系图。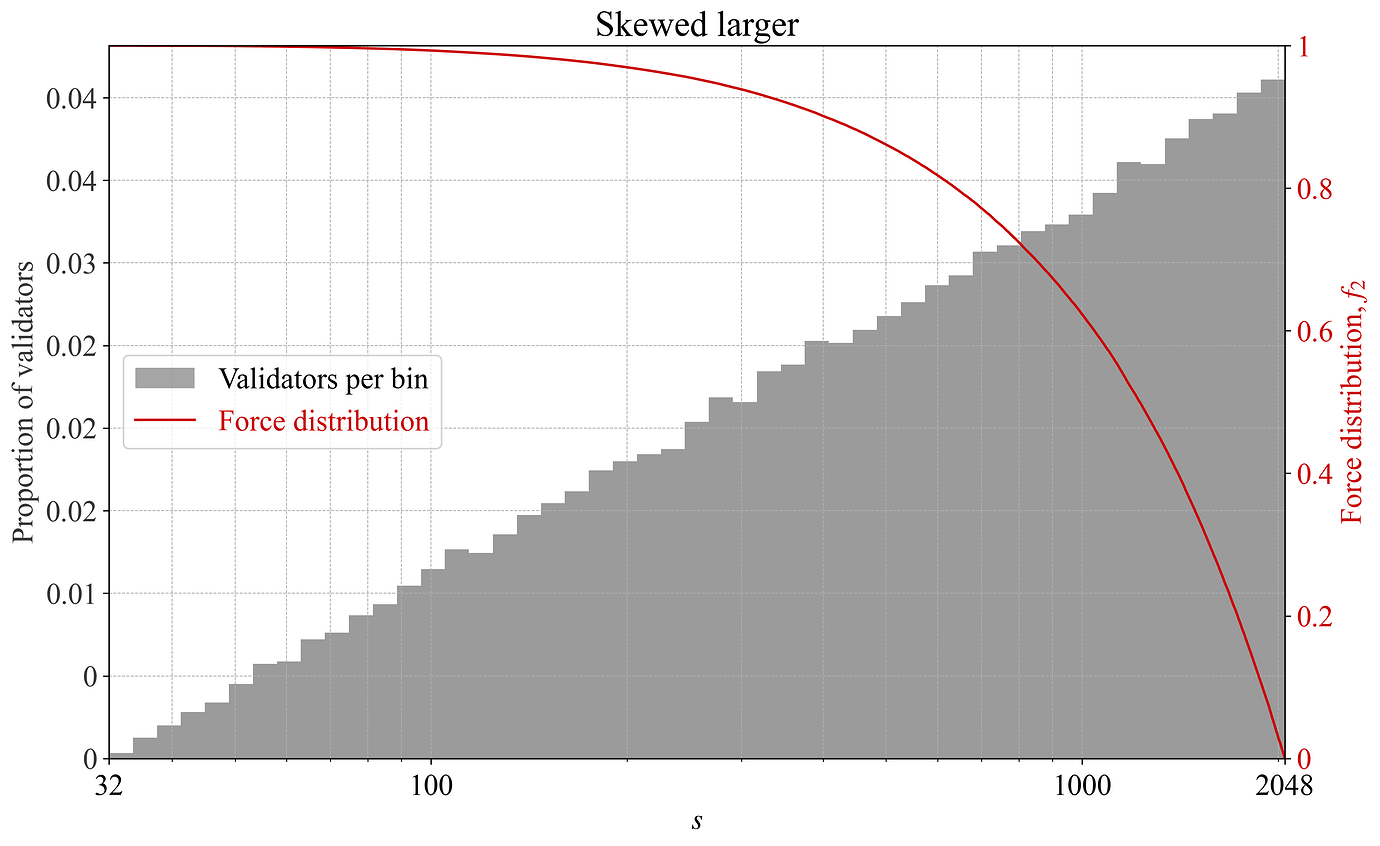 \
Figure 73497×2148 302 KB
\
Figure 73497×2148 302 KB
Figure 7. 在验证者集合偏大的情况下,根据每个 bin 的验证者数量绘制的力分布 f_2。
Figure 8. 在验证者集合偏大的情况下,根据每个 bin 的 ETH 总量绘制的力分布 f_2。
如果验证者聚集在某个特定大小,这可能意味着这个大小提供了最佳的风险/回报。那么,力分布将自动适应,目标是为验证者规定一个“更公平”的收益率。图 9-10 提供了一个例子,其中验证者大小有两个峰值,并且力分布中有一个相应的反应。为了说明的目的,这个例子相当明显。实际上,可能会有更微妙的峰值和谷值,因此 f_2 的变化也会更微妙。
Figure 9. 在具有局部峰值的验证器集合下,根据每个 bin 的验证器数量绘制的力分布 f_2。
Figure 10. 在具有局部峰值的验证器集合下,根据每个 bin 的 ETH 总量绘制的力分布 f_2。
使用 32 ETH 和 2048 ETH 边界上验证者的活动余额的离散化度量可能是有益的,以避免对余额的微观管理。例如,所有介于 32-33 ETH 之间和 2040-2048 ETH 之间的验证者可能会收到相同的 f_2,该 f_2 计算为该范围内验证者中最低和最高 f_2 的平均值。出于计算的原因,可以考虑在其他范围内进行离散化,但大概只会导致更多的余额微观管理。
由于 CID 引入了额外的复杂性,如果要采用它,其好处必须是显著的。那么,如果总体策略是要推行,首先发布一个纯粹的 AID 似乎是合理的。如果以后有必要,可以随时引入 CID 覆盖。
3.3 BID —— 在 AID 和 CID 之间取得平衡
自然地,可以考虑 AID 和 CID 的混合度量,这里称为 BID。 这是一种尝试避免单独使用时这两种变体的问题方面的方法。 因此,为验证者计算 AID f_2 和 CID f_2,最终的 f_2 是两者的加权平均。 那么,使用 CID 下的 AID 作为 AID 的度量似乎很自然。
4. 合并力标度 f_y
合并力标度 f_y 决定了在合并力在 0 和 1 之间时,收益率应该改变多少。它也可以用于缩放年度发行总量,届时表示为 f_I。 这是用于合并激励的三个最终参数。 回顾先前的内容,在衰减模式下,集体激励的完整公式为
f_1f_y,
对于个人激励,公式为
f_1f_2f_y.
适当的 f_y 将取决于当前提供的收益率、相对于收益率可用的 MEV 量、作为质押者的感知风险、质押集合的组成等等。 因此,采用时 MEV 燃烧的存在等因素会影响适当的规模(详见下文第 4.2 和 4.4 节中的讨论)。
太弱的合并力度将无法充分鼓励合并。 太强的个人激励将被(理所当然地)解释为以太坊对较小的验证者不公平。 如果一方的行为会对另一方的收益率产生重大影响,那么强大的集体(和个人)激励可能会导致共识参与者之间的摩擦。 例如,如果没有个人激励,并且一些 SSP 为了降低风险而取消合并,同时显着降低每个人的收益率,这可能会导致特别强烈的摩擦。
以下小节概述了 f_y 的四种设计。 正确的方法将取决于奖励曲线的形状,因此发行策略的改变可能会影响哪种方法是最佳的。
4.1 发行收益率的一部分
一种方法是按发行收益率的一部分进行缩放
f_y=k_1y_i,
或相应地按发行量的一部分进行缩放
f_I=k_1I.
如果发行收益率为 1% 且力为 1,则设置 k_1=0.1 会导致收益率降低 0.1%。
使用发行收益率的一部分背后的想法是,均衡质押收益率意味着一些关于质押风险的信息。 如果均衡收益率很高,可能需要比收益率低时更大的激励来鼓励合并。 因此,质押者会因降低风险(或占据共识位置)而被收取一部分收入。 一个缺点是,发行收益率不是目前质押者获得的唯一奖励:MEV 公平等同于所有质押者,并且此收入不会反映在 k_1y_i 中。 另一个问题是,均衡收益率还会补偿质押的其他更一般的“成本”(例如,硬件),并且这些质押成本受验证者的活动率的影响要小得多。
4.2 固定 ETH/年
另一个想法是通过以下方式将规模推导为固定 ETH/年
f_y=k_2/D,
或相应地
f_I=k_2.
如果力为 1,则设置 k_2=60\,000 将在 60M ETH 质押时导致收益率降低 0.1%。
如果奖励主要由 MEV(包括优先级费用)主导,并且 MEV 大致保持不变,那么这种缩放激励的方式将非常有效。 质押收益率仍然随存款规模而变化,因为固定 MEV 必须分配给所有质押。 因此,合并激励将随质押收益率而变化,而不会过多地关注不太相关的发行收益率。
4.3 固定收益率,与发行和 MEV 无关
第三种选择是指定一个固定的收益率组成部分,即简单地
f_y=k_3,
或相应地
f_I=k_3D.
如果力为 1,则设置 k_3=0.001 将导致收益率降低 0.1%。
通过这种设计,名义激励将保持不变,而与质押收益率的水平无关(如果 f_1 和 f_2 保持不变)。 如果与作为质押者相关的风险保持不变,以至于收益率的均衡变化并不意味着此类风险的变化,那么这种方法可能是合理的。 如果质押供给曲线相当平坦并保持固定,这也可能是合适的。 在这种情况下,MEV 的任何变化都将被存款规模的变化所抵消,因此均衡收益率也将保持固定。 也可以在变化的供给曲线下为该设计提供概率论证,其奖励曲线与当前的曲线非常相似。 然后,高存款规模的均衡可能与 MEV 的增加相关(因为否则供给曲线将需要不可思议地降低)。 该建议是,在存款规模上,最可能的质押收益率比仅奖励曲线所指示的更加固定。
4.4 混合 f_y——y_i 的一部分和固定 ETH/年
力标度可以是先前几个建议的混合体,因为它们可以相互补充。 例如,规范可以是
f_y=k_1y_i + k_2/D,
或相应地
f_I=k_1I + k_2.
使用先前讨论的设置和 D = 60\text{M} ETH,如果在此存款规模下提供 1% 的发行收益率,则结果将是
f_y=0.1\times0.01 \;+\; 60\,000/60\,000\,000 = 0.002,
因此为 0.2%。 建议的混合 f_y 可以被视为将合并激励与发行和 MEV 收益率相关联的一种尝试,从而与整体质押收益率相关联,这似乎是一个理想的目标。 这可以用稍微不同的方式表示为
f_y=k_1(y_i + y'_v),
其中 y'_v 是 k_2/D,但被重新定义为 MEV 收益率的估计值。 在此公式中,k_1 调节 y_i 和 y'_v 的强度——它们共同表示质押收益率。 目前无法直接计算(“看到”)MEV,因此需要在其域之外进行更新。 可以考虑的是就计算 y'_v 的某种商定的方式,或者就此而言,将其固定在当前水平并承诺仅在实行 MEV 燃烧时才对其进行更改。 例如,假设力标度设置为质押收益率的 k_1 = 20\%。 那么,该方程变为 0.2(y_i + y'_v)。 作为指导,2023 年有310k ETH 的 MEV 通过 MEV boost 分发。 2024 年降至约 220k ETH。 仅依靠 MEV boost,在 34M ETH 质押时,y'_v 的粗略长期估计值可能为
y'_v=\frac{0.22\times10^6}{34\times10^6}\approx0.0065.
该估计始终与年度 MEV 有关,而不是与 MEV 收益率有关。 存款规模 D 由协议已知,就像发行收益率一样,不需要估计。 在 34M ETH 质押时,理想共识性能下的发行收益率约为 2.85%,因此最大激励将为
f_y=0.2(0.0285 + 0.0065)=0.2\times0.035=0.007,
即 0.7%。 这是一个相当强大的激励,尽管仅在完全取消合并的验证者集合(f_1=1)下激活。 即使希望最终追求如此强大的激励,以较小的 k_1\leq 0.1 开始仍然是合理的。
5. 衰减、提升或发行中性激励
个人激励有三种可能的模式:衰减、提升或发行中性(相对于奖励曲线);集体激励有两种模式:衰减或提升。 集体激励永远不能是发行中性的,因为该机制的要点是集体(对每个人)根据合并级别调整奖励。 本节回顾了可能模式的优点和缺点,并重点介绍了它们之间的等效性。 结论是衰减激励是最可取的,而发行中性激励是第二好的选择(适用于个人激励)。 为了清楚起见,表 1 指定了不同模式的基线方程,假设 f_1 和 f_2 的计算方式如第 2-3 节所述,发行中性方程如第 5.2.1 节所述。
| 列 1 | 集体 | 个人 |
|---|---|---|
| 衰减 | -\,f_1f_y | -\,f_1f_2f_y |
| 提升 | +\,(1-f_1)f_y | +\,f_1(1-f_2)f_y |
| 发行中性 | -\,f_1(f_2-\frac{\sum_{i} f_{2(i)}s_i}{\sum_{i} s_i})f_y |
表 1. 集体激励和个人激励不同模式的基线方程,当 f_1 和 f_2 的计算方式如第 2-3 节所述,发行中性方程如第 5.2.1 节所述时。
5.1 集体激励的最佳模式
5.1.1 等效性
集体激励的模式不如个人激励的模式重要,因为集体激励中的衰减和提升模式可以等效。 假设较高的奖励曲线 A 被衰减,较低的奖励曲线 B 被提升,并将它们之间的差异设置为力标度 f_y(忽略关于其计算的复杂性)。 此外,在任何 V 下,对于 A,设 y_c = f_1(V)f_y,对于 B,设 y_c = (1-f_1(V))f_y。 那么,对于 A,y_i-y_c 将等于对于 B,y_i+y_c:
f_y + [y_c-f_1(V)f_y] = [y_c + (1-f_1(V))f_y],
f_y-f_1(V)f_y = f_y-f_1(V)f_y.
该等式很容易实现,并且所选模式将不会影响共识参与者的实际激励。
5.1.2 清晰度
但是,该模式仍然具有一定的相关性。 使用衰减模式,奖励曲线会规定最大可能的发行量——这是一个需要明确编码的重要特征。 在提升模式下,仍然可以推断出最大可能的发行量,但这需要将 f_y 添加到奖励曲线。 然后,奖励曲线会规定当质押集合取消合并时,理想性能下最小可能的发行量——这是一个稍微不重要的特征。 虽然最小可能的收益率与质押者以及作为通用设计标准相关,但实际结果也会受到特殊职责分配(例如,区块提议)的运气、其他共识参与者的行为等的影响。 在任何一种情况下,仍然可以通过扣除 f_y 来计算衰减激励下理想性能的最小可能收益率。
5.1.3 重新参数化的影响
如果在不更改奖励曲线的情况下重新参数化集体激励,它将影响提升激励下的最大发行量和衰减激励下理想证明的最小发行量。 在这种情况下,对于提升激励,两种可能的结果是最大发行量增加(非常敏感)和最大发行量减少(不太敏感)。 对于衰减激励,两种可能的结果是理想性能下的最小发行量增加(不太敏感)和理想性能下的最小发行量减少(敏感)。 从政治上讲,不得不增加最大发行量(或更改奖励曲线)以实现更强的集体激励可能是最具问题的。 但是,减少到最小也会在政治上很敏感。 这表明提升激励会使未来的更改在社会上更昂贵。
顺便说一句,请注意,对集体激励的任何有预谋的更改都是有问题的。 开发人员应从一开始就对效用最大化的激励进行编码。 例如,如果已知或怀疑 f_1 或 f_y 在某些结果下将进行调整,例如,在良好合并下减少提升,那么首先根本不存在合并的集体激励(参见 生产策略中的棘轮效应)。
要考虑的另一件事是由于 y'_v 的变化而导致的重新参数化。 如果追求第 4.4 节中的参数化:f_y=k_1(y_i+y'_v),则最大值或最小值可能会在 y'_v 更改时更改。 同样,必须考虑对增加和减少的敏感性,特别是每次 y'_v 增加时都会增加峰值发行的缺点。
5.2 发行中性个人激励
5.2.1 概述
在比较个人激励的模式之前,将介绍发行中性模式。在衰减模式下,f_2 的范围为 0-1,小/非活跃验证者接近 1,大/活跃验证者接近 0。然后,从每个验证者的目标发行收益率中减去从 f_1f_2f_y 得出的合并激励 y_c。“发行中性”方法计算全局线性位移 f'_2 = f_2-d,使得总发行量不受影响,同时保持小(非活跃)验证者和大(活跃)验证者之间的收益率差异。这最终通过负 f_2 提升大/活跃验证者的收益率,并通过(较小的)正 f_2 衰减小验证者的收益率(但相对较少)。具体来说,当按大小加权时,所有 f'_2\text{s} 的平均值变为 0。设 s_i 为验证者 i 的大小,f_2(i) 为其力分布。然后,可以从以下公式计算发行中性位移 d
d = \frac{\sum_{i} f_{2(i)}s_i}{\sum_{i} s_i}.
鉴于 d 对所有验证者均适用,因此可以理解为反映集体激励。 但是,在此上下文中,最好将其描述为“反集体激励”。 衰减或提升个人激励将产生的任何总收益率变化,变量 d 都会进行恢复——对每个人都采取相同的措施——使总收益率不受合并级别的影响。 请注意,这意味着提升和衰减个人激励也包含一些集体激励——提升个人激励将增加总收益率,而衰减个人激励将减少它。 发行中性方法从个人激励中消除了集体激励的任何痕迹。
y_c = f_1f_y(c+f_2) 的合并激励联合公式中 c 的作用可以与强制执行 f_2-d 的位移 d 的作用进行比较。 区别在于 c 被添加而 d 被减去,因此 c \equiv -d。 因此,明确了衰减或提升个人激励的集体部分。 由此可见,如果以太坊同时使用集体激励和个人激励,则应联合对其进行分析。 考虑到这一点,请注意,本节开头表 1 中的提升个人激励最终比衰减对应方高出 f_1f_y。 因此,它们被一个集体组成部分分开,并且可以通过移动 f_1f_y 使它们相等。
请注意,c 是预先固定的,并且 d 是从 f_2 计算得出并随之变化的。 c 的强度可以根据协议的需求进行调整,但是也可以将调整后的强度用于 d。 可以将此调整规定为 d' = dk_d。 对于 0<k_d<1,d' 将看到个人激励的集体部分位于发行中性和衰减模式之间。 最后,可以提到一点,对于个人验证者而言,总的来说重要性自然较低,重要的是对其 f_2 的直接更改——至少在进行任何相关的均衡变化之前。
5.2.2 基本原理
可以确定发行中性个人激励的两种好处,这两种好处与较低或没有集体激励相结合时更加重要。 首先,协议发行将最终更接近奖励曲线所规定的发行水平(而与合并水平无关),这可以说是提高了设计的清晰度。 其次,建议的以太坊发行策略的一种方法是确保勤奋的 32-ETH 单独质押者始终获得积极的定期奖励。 同时,希望在高存款比率下将奖励曲线设置为接近 0。 发行中性个人激励允许以太坊在低合并下将小型验证者的收益压缩到更接近良好合并下提供的收益,从而可以将奖励曲线规定为更接近 0,同时仍然确保积极的定期奖励。 在低合并下,f_1 最高。 此时,小型验证者多于大型验证者,并且只需稍微减少小型验证者的奖励即可保持中立性(与此同时,少数大型验证者的奖励将得到更大幅度的提高)。
5.2.3 模拟
为了说明发行中性个人激励对较小的 32-ETH 验证者的收益差异的压缩,生成了具有平滑变化的齐普夫分布的验证者集合。 附录 C 中提供了该方法的详细说明。 通过将 [0, 1] 范围内的等距均匀分布 u 馈入以下公式来生成每个验证者集合
\Bigl( s_{\text{min}}^\alpha+u\bigl(s_{\text{max}}^\alpha - s_{\text{min}}^\alpha\bigr) \Bigr)^{\tfrac{1}{\alpha}}.
在此公式中,每个验证者集合的组成都由指数 \alpha 控制,其中 \alpha=-1 导致验证者的齐普夫分布。 附录 C.1 说明了 \alpha 的影响。 该等式的积分将验证者大小 V 与存款大小 D 相关联,因此可以采用闭式解来近似给定特定 D 和 \alpha 的验证者数量,如下所示:
V \approx \frac{D(\alpha+1)\bigl(s_{\text{max}}^\alpha - s_{\text{min}}^\alpha\bigr)}{\alpha\bigl( s_{\text{max}}^{\alpha+1} - s_{\text{min}}^{\alpha+1} \bigr)}.
附录 C.2 介绍了推导过程。 图 11 说明了在 80M ETH 的质押中,发行中性策略对 32-ETH 验证者的影响。 它是为 -6 到 2 之间的 \alpha 创建的,在每个点都从前面的等式中计算出近似 V,在特定的 \alpha 处生成验证者集合,并计算发行中性位移 d。 使用了在 (V_{\text{min}}+V_Z)/2 处达到 0 的线性 f_1 ,以及对数缩放的 f_2。 然后,具有位移力 f'_2 的验证者的新发行中性力 f' 变为 f'=f_1f'_2。
Figure 11. 针对 32-ETH 验证者的发布中性力聚合的模拟。对于小验证者来说,衰减力在任何合并级别都可以为 f_2=1,因此最大 f 也为 1(细黑线)。 仅当几乎没有验证者具有最小值时,发布中性的 f'_2(蓝色虚线)才会接近 1,并且在与 f_1(蓝色点线)相乘之后,聚合的 f'(黑线)在 0.1 左右达到峰值。
如图所示,仅在合并的验证者集合下,32-ETH 验证者的 f'_2 才会接近 1。 然后,较大的验证者持有所有 ETH 的明显多数,为了保持发布中性策略下的收益差,必须通过大幅减少小型验证器来进行补偿,这样它们才会有少量收益。 但此时应将 f_1 设置为接近零,因为验证者集合已经合并,如果收益差很大,则会被认为是不公平的。 因此,32-ETH 验证者的发布中性聚合力 f' 从未超过 0.12。 与使用衰减策略(当低合并时 f 将接近 1)相比,这允许将奖励曲线推得更接近零,同时确保获得积极的定期奖励。
5.3 个人激励的最佳模式
5.3.1 不同模式的总体、个人和均衡结果
当验证者集合取消合并时,个人激励应具有较高的收益率差异,这可以通过让 f_1 接近 1 来实现。 因此,在提升个人激励方面的一个关键问题是总收益率的上升(详见第 5.2.1 节中的讨论):取消合并且集体获得奖励。 请注意,这与提升集体激励的工作方式相反(从查看表 1 中的方程可以明显看出),在这种情况下,会奖励合并(如果验证者集合是合并的,则 f_1 必须接近 1)。 但是,与发布中性激励一样,必须考虑 f_1 和 f_2 的交互。 将跨验证者集合的平均 f_2 定义为按权益加权的 \bar{f_2}(实际上,这与先前为 d 计算的度量相同)。 图 12 显示了通过质押的 ETH \bar{f} 的平均力,按该力将集体提升发行量(在按 f_y 缩放后),使用与先前图 11 相同的验证者分布和 f_1 和 f_2 的形状。由于 d 抵消了 f_2 为 0(图 11)的 32-ETH 验证者,并且提升激励依赖于 1-f_2(图 12),因此图 11-12 显得相同,即使它们说明了两个不同的概念。随着合并级别降低,1-\bar{f_2} 的下降缓和了提升激励的实际集体结果,即使发行量下降到超过 100 万个验证者的范围。 这突出了即使采用提升个人激励,发行量也可能不会大幅上升。
Figure 12. 分析了个人提升激励的集体效应。 对于权益质押的 ETH,其力在 0.12 左右达到峰值。 将此点按 f_I 缩放,即可在附录 C 的线性 f_1 和对数缩放的 f_2 的分布下最大程度地增加可行的发行量。
图 13 反而显示了每个权益质押的 ETH 的平均力 \bar{f},通过该力将集体衰减发行量。 随着合并的减少,f_1 和 \bar{f_2} 都会上升,这反映在 \bar{f} 中。这意味着个人衰减激励的“集体”部分比其提升对应物强大得多。
Figure 13. 分析了个人提升激励的集体效应。 随着 D 接近最大值,每个权益质押的 ETH 的力接近 1,从而使发行量最多减少 f_I。
质押者可能会主动取消合并,以便在提升个人激励下直接获利。 持有许多大型验证者的质押者如果将其中的一个验证者划分为几个较小的验证者,将会看到所有剩余的验证者变得更有利可图。 如果 f_1 曲线的局部导数很大,并且没有执行衰减集体激励,则其余验证者中的收益可以抵消已取消合并的验证者的损失。 出于这些原因,如果没有集体激励,提升个人激励的某些实施方案将非常成问题。 当存在集体激励时,必须考虑其幅度——从第 5.2.1 节中可以回想,提升个人激励为所有质押者提供的收益率比衰减个人激励高出 f_1f_y(这个事实也可以从图 12-13 中的黑线总和等于蓝色点线中看出)。 一般的建议是不追求提升个人激励,除非采取措施永远不要激励解除合并。
那么发布中性个人激励应该如何做? 可以注意到,由于合并级别不会影响发行量,因此取消合并大型验证者的质押者的损失将由所有其他验证者的汇总收益来精确抵消。 这减轻了对在解除合并下获得集体收益的担忧,但是实施取消合并的质押者仍然可能会受益。 随着 f_1 增加,大型验证者的收益会将增加,而小验证者的收益会下降,如果 f_1 的局部导数很大,则具有许多大型验证者的质押者可能会从理论上从解除合并中获利。 但是,在这些方面的担忧与提升模式中出现的担忧程度不高,并且不应排除发布中性模式鉴于它也能带来好处。 但是,仍然必须检查极端情况,但是通过采用 c>0 或将 d 更改为 d',其中 0<k_d<1(第 5.2.1 节),可以克服此类问题。
请注意,由于收益率的变化,质押者调整其头寸后,均衡效应将小于直接效应。 初始解除合并导致 f_1 增加将激励其他质押者进行合并,从而将 f_1 推回下降。 在衰减模式下,均衡结果可能是一个理论上的问题。 在这种模式下,具有许多大型验证者的质押者可以解除合并,以降低小型验证者的收益,并期望某些质押者停止质押,从而导致其余大型验证者的质押收益率增加。 虽然相当深奥,但对于不同的模式,均衡结果至少会比直接结果相似得多——在大致相同的 f_1 下,大型验证者和小型验证者之间的盈利差保持固定。但是,均衡结果更具推测性,可能会受到个人激励中的集体组成部分的影响,并且生效速度较慢。
5.3.2 各种模式下的集体问题
第 5.1 节中讨论的有关集体激励的问题也适用于个人激励。 这部分是由于第 5.2.1 节中概述的个人激励中也存在集体激励的痕迹。 提升个人激励还会增加最大可能的发行量。 尤其是,不幸的是,衰减个人激励将会特别压低 32-ETH 验证者的发行量。 发布中性激励的优点在于它们不会增加最大可能的发行量,同时在最坏的情况下也不会过多地恶化 32-ETH 验证者的结果。 32-ETH 验证者收益差的这种“压缩”在第 5.2 节中进行了介绍,并在图 11 中进行了说明。
5.3.3 对劝退攻击的影响
最后,请考虑劝退攻击,并附加一个额外的条件,即仅针对特定大小的验证器。 如果Small 验证者成为攻击目标,其中一些将停止质押,并且合并将得到改善。 因此,攻击者可以从集体的合并激励中获益。 但是,衰减的个人激励将直接导致对小型验证者在合并时具体提高收益率,从而缓解了一些顾虑。 进一步请注意,衰减的个人激励(就直接影响而言)使小型验证者进行此攻击相对有利可图,而提升激励使大型激励验证者相对更有利可图。 如果以大型验证者为攻击目标,则集体合并激励会降低收益率,因此只有在实施促进性个人激励的情况下才需要关注此攻击。
6. 结束说明
提出了正朝着 Orbit/Vorbit SSF 中统一激励前进的系统性框架。 提供了统一激励的三个力 f_1、f_2 和 f_y 在各种设置下的优缺点,并仔细检查了它们的最佳模式。 基于该分析,现在将提出最有利的设置,从而得出一种如何激励统一激励的总体规范。
§1. 本文着重于衰减模式,其主要公式为
y_c = f_1f_y(c+f_2).
统一力量的形状由 f_1 确定,规模由 f_y 确定,各验证者之间的分配由 f_2 确定(因此,f_2 对各验证者而言是独一无二的),而统一激励的相对强度由 c 确定。 所得的统一激励 y_c 随验证者的大小而异,并用于更新每个验证者的目标发行产量:
y'_i=y_i-y_c.
§2. 虽然对于个人及任何集体激励而言,f_1 和 f_y 严格来说不是必需相同的,但追求是一项可以实现的现实设计目标。
§3. 让 f_1 的形状基于混合公式,该公式按照第 2.2 节中的概述的进行参数设置并在图 3 中进行了显示。 这是一个多功能的公式,可以对其进行调整以适合在架构接近采用时的需求。
§4. 为了简单起见,使用 f_1 的固定流程,不带任何动态时间成分(第 2.3 节)。
§5. 让f_2 从作为一个纯粹的 AID 开始。 如果依赖于 Vorbit 设计,或一般而言,也依赖于验证者f_2 = w\frac{a_{\text{max}} - a_v}{a_{\text{max}} - a_{\text{min}}} + (1-w)\frac{ s_{\text{min}} ( s_{\text{max}} - s_v ) }{ s_v ( s_{\text{max}} - s_{\text{min}} ) },
在图 4 中以黄色曲线表示。将 w 设置为 0.5 似乎是一个自然的默认选择(在关注 active stake 和已占用验证者位置之间取得平衡),但 w>0.5 也是可行的,并且可以说更公平。即使方向是出于公平考虑而侧重于 active stake,如果 staking 者有足够的资金,w=0.8 也应该足以确保 staking 者在 Orbit 阈值为 1024 时选择 2048-ETH 的验证者而不是 1024-ETH 的验证者。如果混合度量标准是不必要的,例如在阈值为 2048 的 Orbit SSF 中,也可以使用对数缩放的
f_2 = \frac{\log_2\left(s_{\text{max}}/s_v \right)}{\log_2\left( s_{\text{max}}/s_{\text{min}} \right)},
在图 4 中以蓝色曲线表示。也可以在 Vorbit SSF 下将为 s 和 a 计算的两个对数缩放的 f_2\text{s} 平均/加权在一起。
§6. 主要的选择是根据混合方程 f_y=k_1(y_i + y'_v) 定义 f_y,其中 y'_v 是一个长期估计值,只有在 MEV 发生重大变化后(例如,在实施 MEV 销毁后)才进行调整。最好以适度的规模开始,即 k_1\leq0.1。根据固定的 ETH/年(第 4.2 节)确定 f_y 似乎是第二好的选择。
§7. 主要的选择是在个人和任何集体激励方面都使用衰减模式。然而,发行中性的方法也带来了一些好处,因为它能够压缩小验证者的收益可变性。一旦确定了一般设计,就应该进一步考虑和分析。该分析应排除和反驳第 5.3.1 节中概述的有利可图的反整合的极端情况。
§8. 考虑仅使用个人激励,而不使用纯粹的集体激励,即 c=0。如第 5.2.1 节所述,个人激励仍然具有集体效应(在方向上对于衰减激励是正确的)。如果 staking 集合中的紧张关系不是问题,则可以考虑相对适度的集体激励。
附录 A – Zipfian 数量的 staking 者下的近似 V
如第 2.1 节所述,根据 staking 集合的 Zipfian 性来调整整合激励的强度似乎是直观的。例如,当验证者集合与 Zipfian staking 集合一致(当 V \approx V_Z 时),整合激励应该非常小,以维护公平性。因此,希望能够估计 Zipfian 分布下的验证者数量。假设 staking 者整合所有可用 stake 的纯 Zipfian staking 分布,则验证者数量 V 可以根据 Vorbit SSF 帖子中 附录 A 的公式计算。给定一个特定的 D,Zipfian staking 集合大小首先计算为
N_Z = e^{ W \left( \frac{D}{32} e^\gamma \right) - \gamma},
其中 W 表示 Lambert W 函数,\gamma 是 Euler–Mascheroni 常数,约为 0.577。如果最小验证者余额为 32 ETH,则完全整合下的 Zipfian 验证者集合大小变为
V_Z=\frac{N_Z}{64} \left(63+\ln(N_Z/64) + 2\gamma \right).
如果 Zipfian 性本身仅仅是一个粗略的指导方针,并且该方程将成为共识规范的一部分,那么希望能够对 V_Z 进行一些更简单的近似,而不是这些相当复杂的方程。
对于大 x,Lambert W 函数的行为近似为 W(x) \approx \ln x - \ln \ln x。因此,N_z 的近似值为
N_Z \approx \dfrac{ D }{ 32 \ln \left( \dfrac{D}{32} e^\gamma \right) },
其中分子随 D 线性增加,分母随 D 对数增加。线性项在大 D 时占主导地位,此时分母变化相对缓慢。在前两个方程的第二个方程中,从 N_Z 导出 V_Z,线性项再次占主导地位。因此,线性近似应该非常接近,但对数调整或双对数调整的近似会更准确。图 A1 说明了以下四个近似值与 Zipfian 真实值的一致性:
V_Z = \begin{cases} \displaystyle \frac{D}{347} & \text{(linear)} \\ \\[0.1ex] \displaystyle \frac{D}{20\,\ln D} & \text{(log adjusted)} \\ \\[0.1ex] \displaystyle \frac{D}{22.3\,\ln D-15\ln \ln D} & \text{(loglog adjusted)} \\ \\[0.1ex] \displaystyle \frac{D + 1145\sqrt{D}}{409} & \text{(square-root adjusted)}\\ \end{cases}
选择常数是为了偏好整数和简单性。例如,将对数调整方程中的常数设置为 19.9 而不是 20 会使结果与真实值更接近。然而,常数 20 仍然使整个范围内的差异大致相等,约为 1000,并且完全满足我们的目的。包含第四个选项是因为所有共识客户端已经实现了在计算当前奖励曲线时代对 D 进行平方根运算的函数。如果最小验证者余额发生变化,则可以使用以下通用方程
V_Z = \frac{D}{a\ln D}
和
\frac{D}{a\ln D-b\ln \ln D}
可以改为使用。
图 A1. 纯 Zipfian 分布的各种近似值。
图 A2 以更精确的相对比较显示了近似值与计算出的 V_Z 的差异。显而易见的是,loglog 调整的近似值非常接近,但其他近似值也完全满足本规范的目的。
图 A2. 概述的近似值与真实值计算之间的差异。对数调整方程产生的与 1000 个验证者的真实值的距离相当均匀,而 loglog 调整方程几乎是完美的。
附录 B – 与 Orbit SSF 帖子中的激励措施进行比较
B.1 作为 D_a 函数的集体激励
可以与之前在 Orbit SSF 帖子中提出的激励设计进行比较。该帖子 概述 了另一种集体整合激励策略,其中发行直接取决于 active stake I(D_a),而不是总 stake I(D)。
等价性必须基于奖励曲线的方程,以便在 I(D) 规定的发行量可以通过衰减反映回 I(D_a) 的发行量。使用第 4.1 节中定义的整合力尺度:f_I=k_1I,其中 k_1=1。这意味着发行的总衰减 I_c 变为 I_c=f_If_1=If_1。目标是确定 f_1,该 f_1 在当前奖励曲线 cF\sqrt{D} 下,使 I - I_c 变为 I(D_a),当使用 D_a 时,该曲线为 cF\sqrt{D_a}。方程首先展开:
I - I_c = cF\sqrt{D} - cF\sqrt{D}f_1=cF\sqrt{D}(1-f_1).
然后,整合力 f_1 必须简单地反映回发行曲线上的点 D_a。因此,如果 D_a/D stake 是活动的,则当前奖励曲线的 f_1 必须是
f_1=1-\sqrt{D_a/D}.
从先前继续的示例说明了这种等价性:
cF\sqrt{D} \Bigl(1 - \Bigl(1-\sqrt{D_a/D}\Bigr)\Bigr) = cF\sqrt{D}\Bigl(\sqrt{D_a}/\sqrt{D}\Bigr)=cF\sqrt{D_a}.
鼓励读者查看 Orbit SSF 分析,该分析还回顾了 I(D) 和 I(D_a) 之间的相似之处,借助附录 B.2 的方程,可以得出与此处呈现的结果相关联的结果。一个值得进一步考虑的细节是,f_1 是基于验证者数量 V 而不是 active stake D_a 来计算的。当使用 V 时,发行曲线将不受 Orbit 规范的影响。例如,如果调整了 vanilla Orbit 中的阈值 T,则会调整 D_a,从而调整发行/整合激励。这既有潜在的好处,也有潜在的缺点。
当 T=2048 时,V 和 D_a 之间的关系很简单,因为平均验证者大小可以写成
s_{\text{avg}} = \frac{2048D_a}{D}
和
s_{\text{avg}} = \frac{D}{V}.
这意味着验证者的数量是
V = \frac{D^2}{2048D_a}.
B.2 作为 D 函数的集体激励
Orbit SSF 帖子的 附录 进一步建议使用替代方案 I(D)\frac{D_a}{D},这等效于使用 f_I=k_1I(来自第 4.1 节),其中 k_1=1 且 f_1 = 1-D_a/D:
I(D) - I(D)f_1 = I(D)(1-f_1)= I(D)(1-(1-D_a/D)) = I(D)D_a/D.
附录 B.1 中进一步介绍了 D_a 和 V 之间可能的联系。与 Orbit SSF 帖子中的公式更一般的等价性是将 f_1 设置为 1-\delta(D_a/D)。
B.3 个人激励
关于个人激励,Orbit SSF 设计 再次可以理解为 f_y=k_1y_i,其中 k_1=1。还有人建议将规模限制在发行收益的 25%,即类似于设置 k_1=0.25。与 f_2 相对应的方程在 a 中是线性的,如第 3.1.1 节的第一个方程中所示,其归一化版本在图 4 中显示为绿线。然而,Orbit SSF 帖子建议提高收益而不是衰减收益,这解释了与第 3.1.1 节中第一个方程的差异。由于反整合的集体收益,提高的个人激励措施在第 5.3.1 节中被强调为有问题。因此,应避免单独使用它们,但可以注意到,Orbit SSF 帖子采用了强大的集体激励措施来弥补这一点。效果类似于第 5.2.1 节中讨论的补偿效果。
最后,还有一种概念是让与 f_1 相对应的项在某个充分的整合水平上达到 0,此处为 D_a/D=0.8。这可以直接与让 f_1 曲线在 V 方面达到 Zipfian 分布的 staking 者后达到 0 进行比较。
附录 C
C.1 跨 \alpha 模拟的验证者分布
用于模拟 Zipfian 性从第 5.2.3 节平滑变化的方程可能对于此特定研究之外的其他情况也很有用。因此,本附录提供了有关先前提出的方程的更多见解和详细信息。首先生成验证器
\Bigl( s_{\text{min}}^\alpha+u\bigl(s_{\text{max}}^\alpha - s_{\text{min}}^\alpha\bigr) \Bigr)^{\tfrac{1}{\alpha}}
并考虑当 \alpha=-1 时的 Zipfian 情况。在这种情况下,指数变为 1/-1=-1,方程为
\frac{1}{1/32+u(1/2048-1/32)}.
0 的第一个均匀分布的样本将产生大小为 1/(1/32)=32 的验证器,而 1 的最后一个样本将产生大小为 1/(1/2048)=2048 的验证器,这是必需的。u 中相等间距的倒数用于生成调和级数。因此,该方程重新创建了 Vorbit SSF 帖子的 第 2.1 节 中的基线方法(这次应用于验证器而不是 staking 者),但以一种可以推广到随 \alpha 平稳变化的非 Zipfian 分布的形式。当 \alpha=-1 时,大约一半的验证器的余额低于 64,这符合调和级数的预期。当 \alpha<-1 时,验证器在低余额时间隔更紧密,导致验证器集合的整合程度较低,而当 \alpha>-1 时,验证器在高余额时间隔更紧密,导致集合的整合程度更高。图 C1 显示了在每个直方图条中以总 ETH 计的 \alpha=-1.9(绿色)、\alpha=-1(橙色)和 \alpha=-0.1(蓝色)的结果。请注意,在模拟中必须始终避免 \alpha=0,因为 1/\alpha 会变为无穷大。
图 C1. 三个验证器分布的 stake 加权直方图,stake 数量为 8000 万 ETH。较高的 \alpha 给出的分布整合度更高,而 \alpha=-1 给出的验证器分布是 Zipfian 分布。
C.2 在任何给定 D 下近似 V
附录 C.1 中方程的积分可用于捕获验证器数量(可以将其视为图 C1 中 x 轴上的样本)与 ETH 总量(曲线下的结果面积)之间的关系:
I_u =\int_{0}^{1} \Bigl( s_{\text{min}}^\alpha + \bigl(s_{\text{max}}^\alpha - s_{\text{min}}^\alpha\bigr)u \Bigr)^{\frac{1}{\alpha}}du.
封闭形式的解是
I_u = \frac{\alpha}{(\alpha+1)\bigl(s_{\text{max}}^\alpha - s_{\text{min}}^\alpha\bigr)} \bigl(s_{\text{max}}^{\alpha+1} - s_{\text{min}}^{\alpha+1}\bigr).
该积分可以理解为规定平均验证器大小,因为它涵盖了均匀分布 u 中的范围 0-1。由此可见,存款大小可以生成为 D=VI_u,因此 I_u=D/V。代入后得到
\frac{D}{V} = \frac{\alpha}{(\alpha+1)\bigl(s_{\text{max}}^\alpha - s_{\text{min}}^\alpha\bigr)} \bigl(s_{\text{max}}^{\alpha+1} - s_{\text{min}}^{\alpha+1}\bigr),
最后可以将 V 的近似值求解为
V = \frac{D(\alpha+1)\bigl(s_{\text{max}}^\alpha - s_{\text{min}}^\alpha\bigr)}{\alpha\bigl(s_{\text{max}}^{\alpha+1} - s_{\text{min}}^{\alpha+1}\bigr)}.
- 原文链接: ethresear.ch/t/consolida...
- 登链社区 AI 助手,为大家转译优秀英文文章,如有翻译不通的地方,还请包涵~
- 意图聚合器比传统交换更流畅吗? - CoW DAO 106 浏览
- 以太坊区块构建管道:去中心化之路 183 浏览
- 区块链中的“黑暗森林”:理解MEV与捕食性动态 – ImmuneBytes 174 浏览
- 什么是DeFi?去中心化金融指南 - CoW DAO 312 浏览
- L1 价值捕获的压缩 256 浏览
- DeFi和加密货币之间有区别吗?——CoW DAO 422 浏览
- 什么是DeFi聚合器?——CoW DAO 258 浏览
- 顶级DeFi交易所:理解去中心化交易基础设施 - CoW DAO 415 浏览
- 如何开始你的第一个 Uniswap V4 Hook:要点、库与风险 11 浏览
- Solana的区块构建之战 344 浏览
- 如何去中心化构建区块? 428 浏览
- CoW DAO月度回顾:2026年1月 - CoW DAO 416 浏览
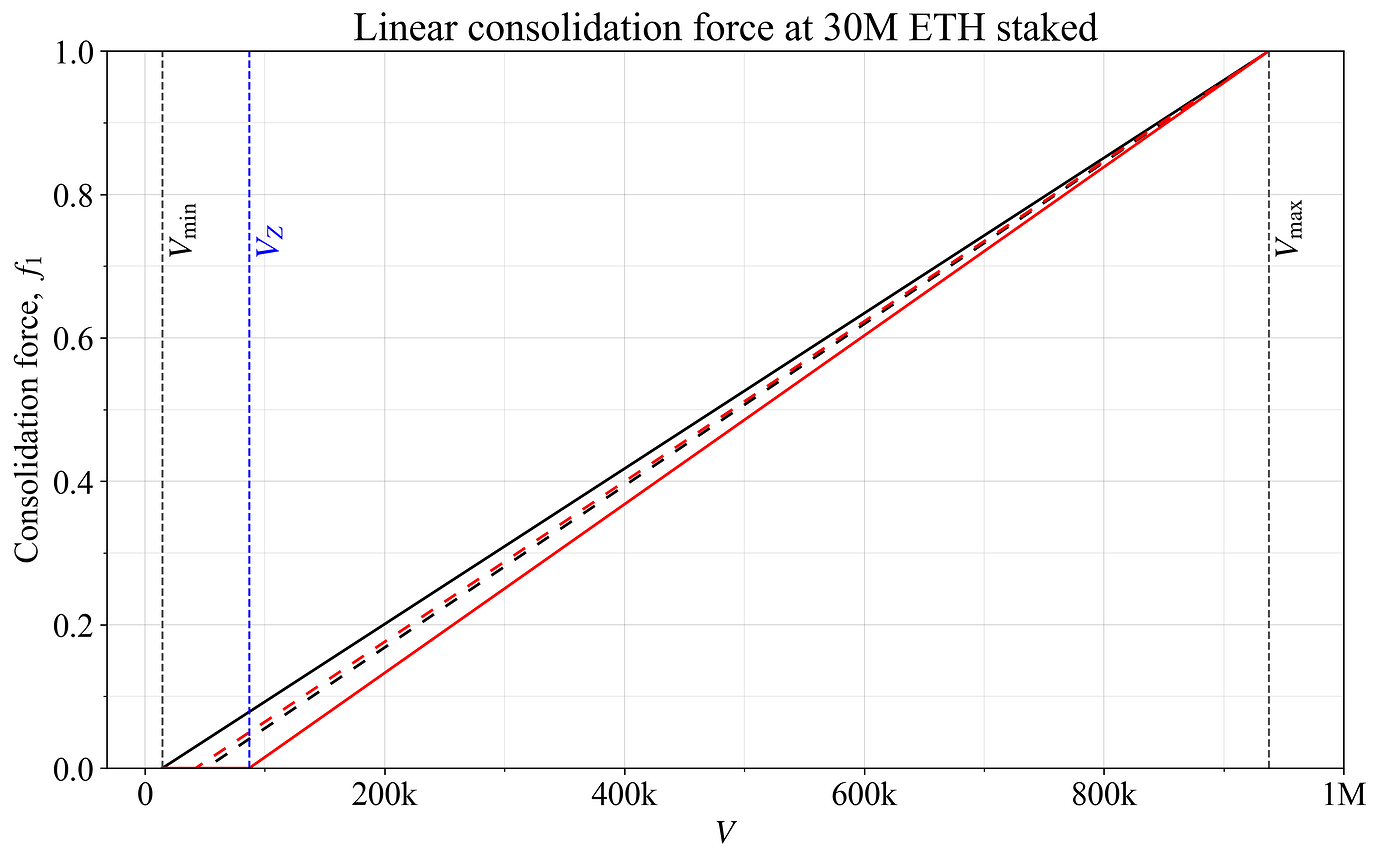 \
图 13113×1948 271 KB
\
图 13113×1948 271 KB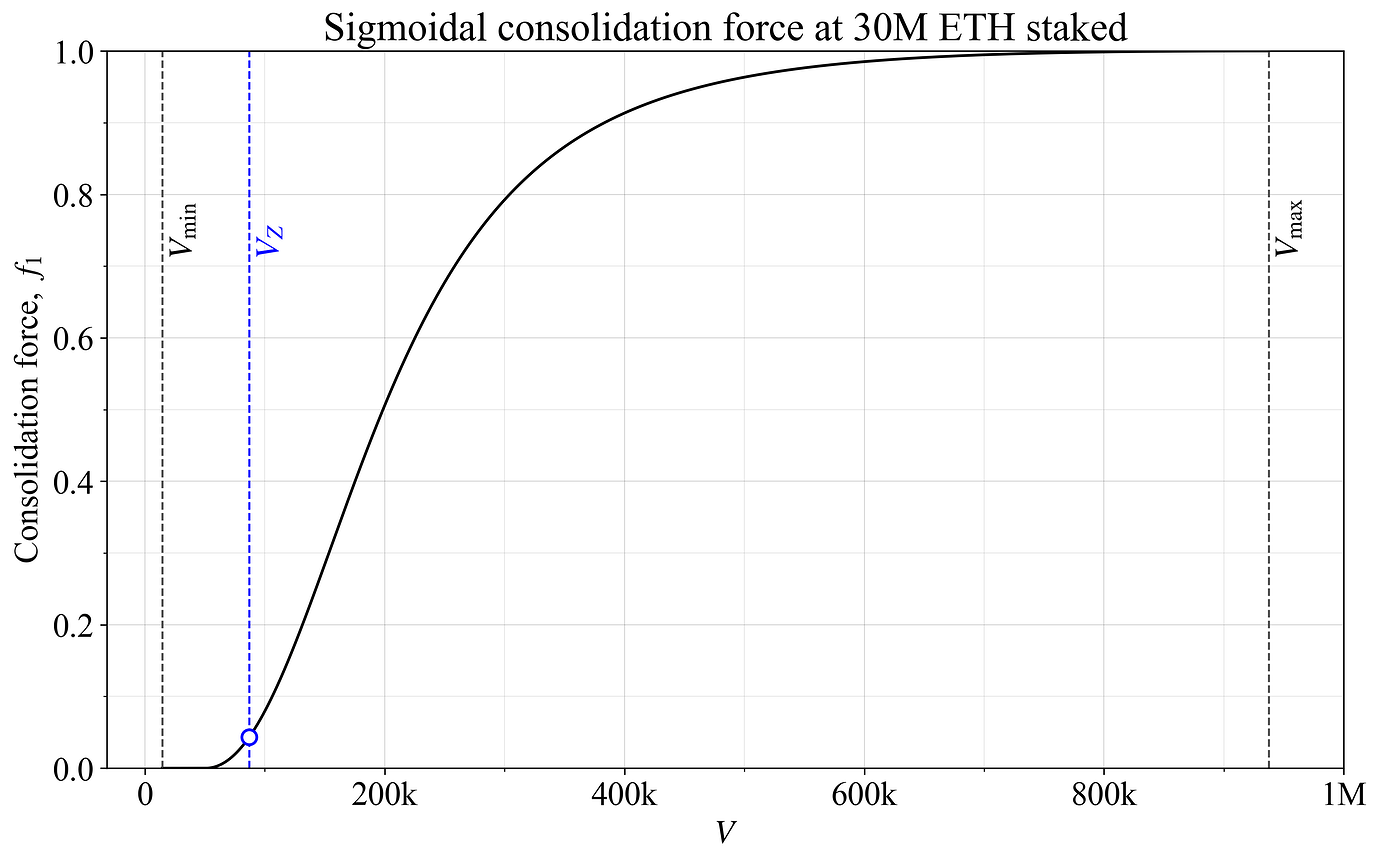 \
图 23113×1948 188 KB
\
图 23113×1948 188 KB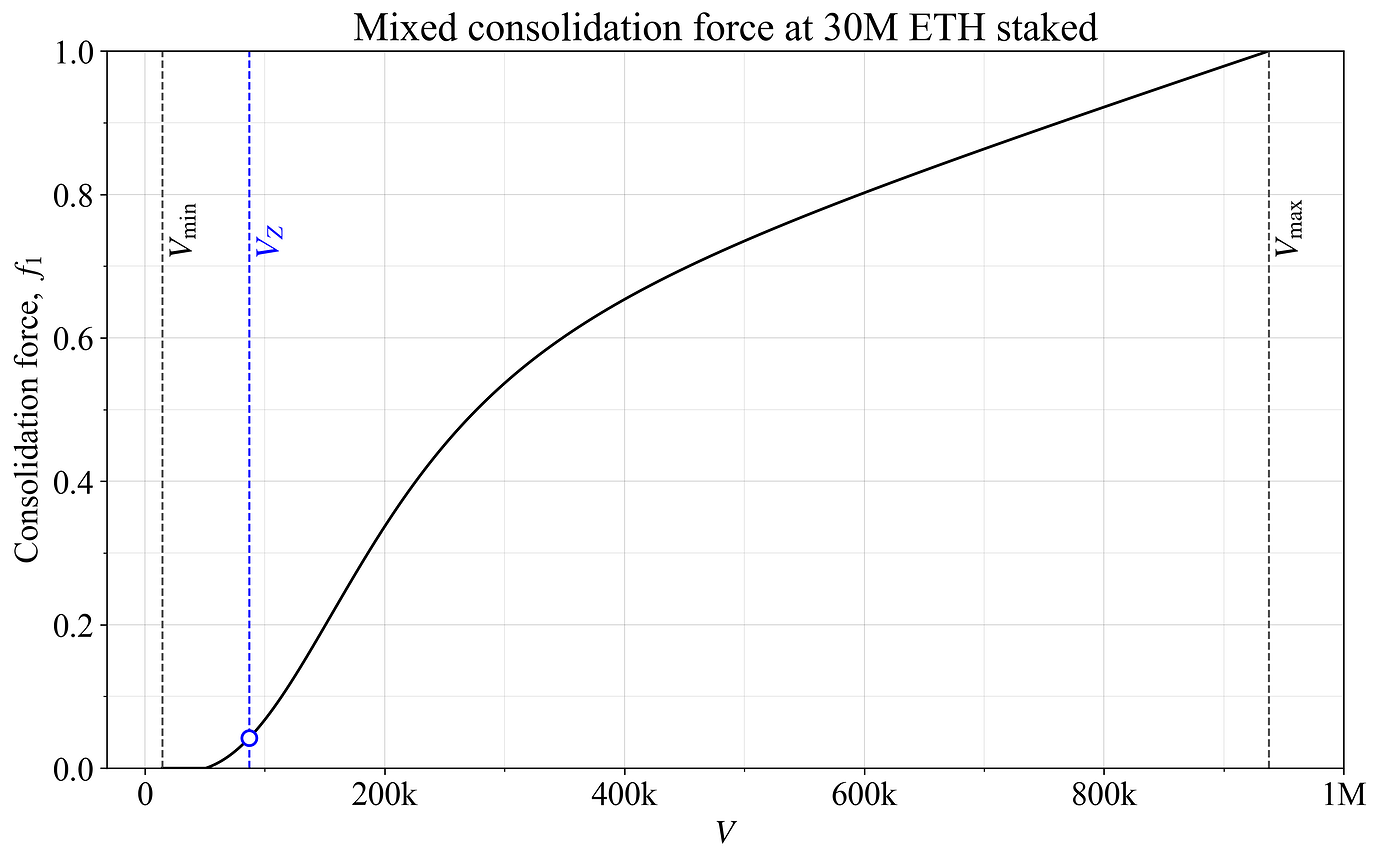 \
图 33113×1948 195 KB
\
图 33113×1948 195 KB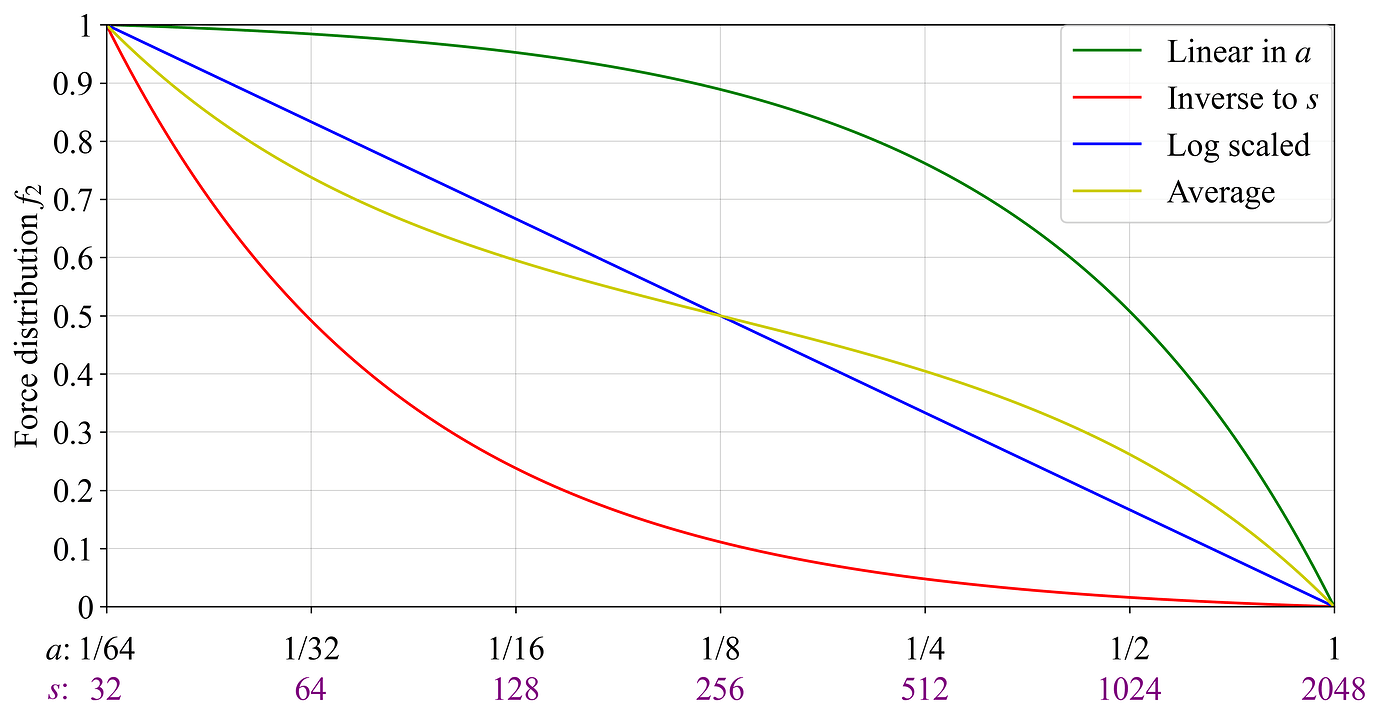 \
图 43136×1637 337 KB
\
图 43136×1637 337 KB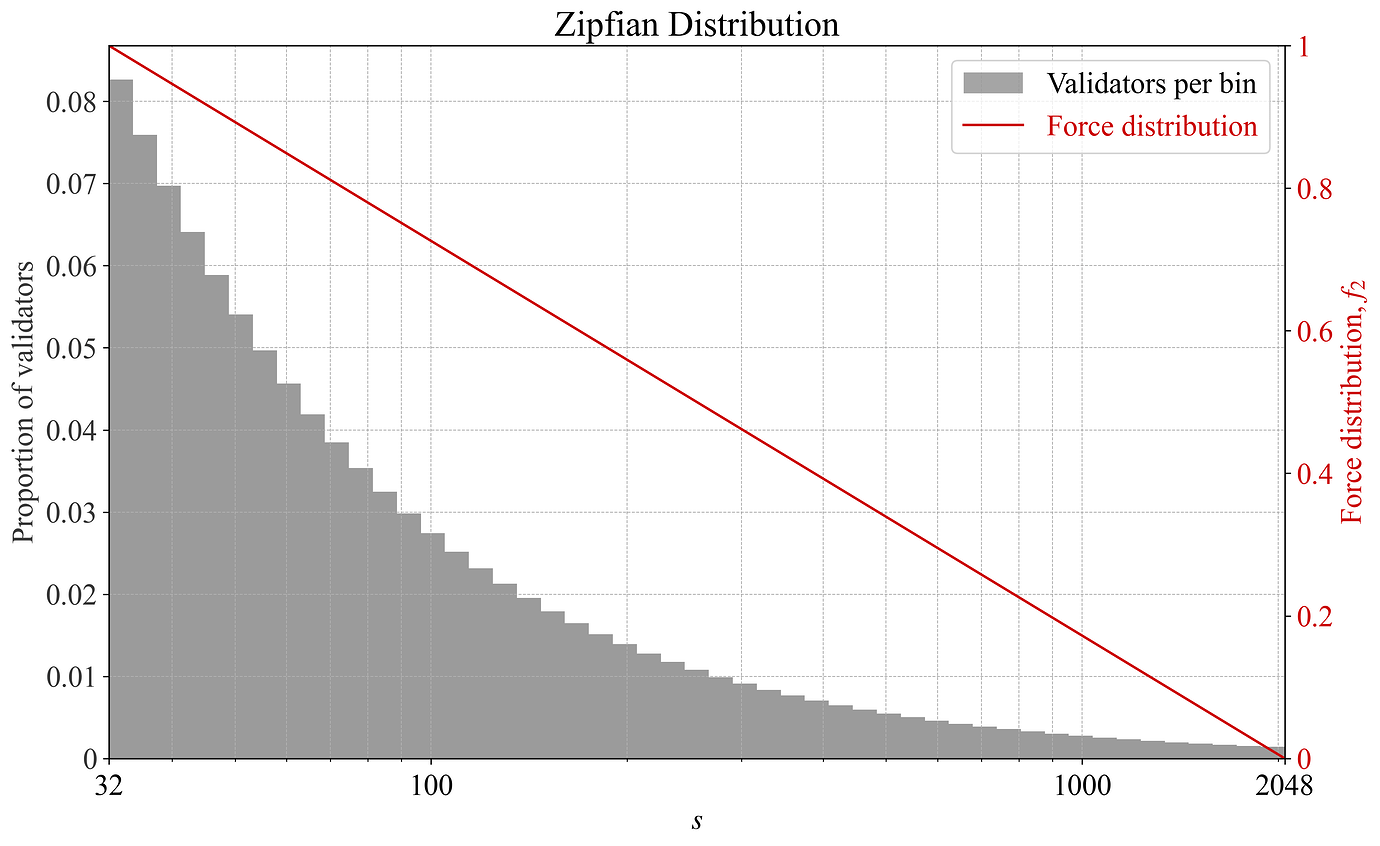 \
图 53497×2148 327 KB
\
图 53497×2148 327 KB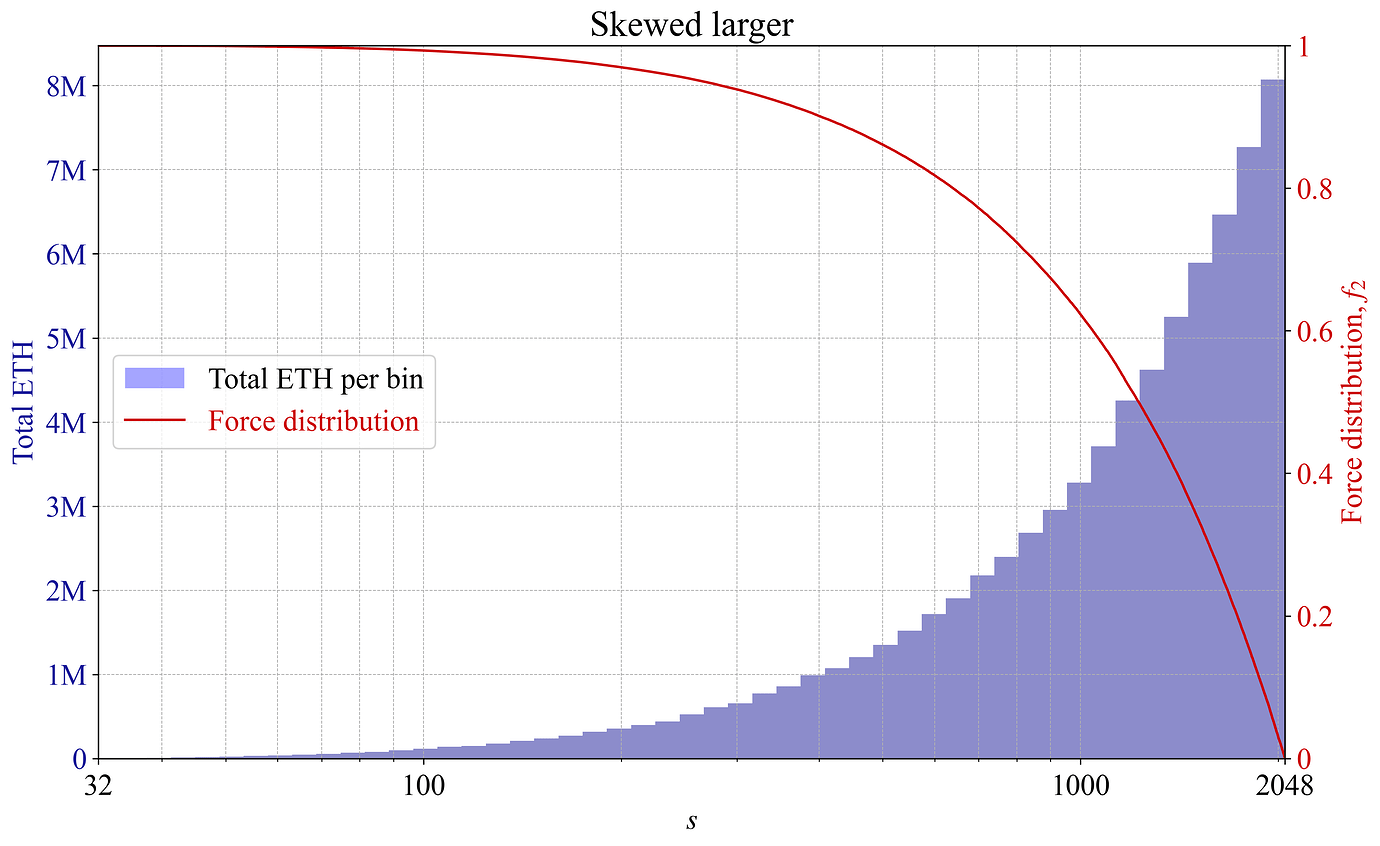 \
Figure 83496×2148 286 KB
\
Figure 83496×2148 286 KB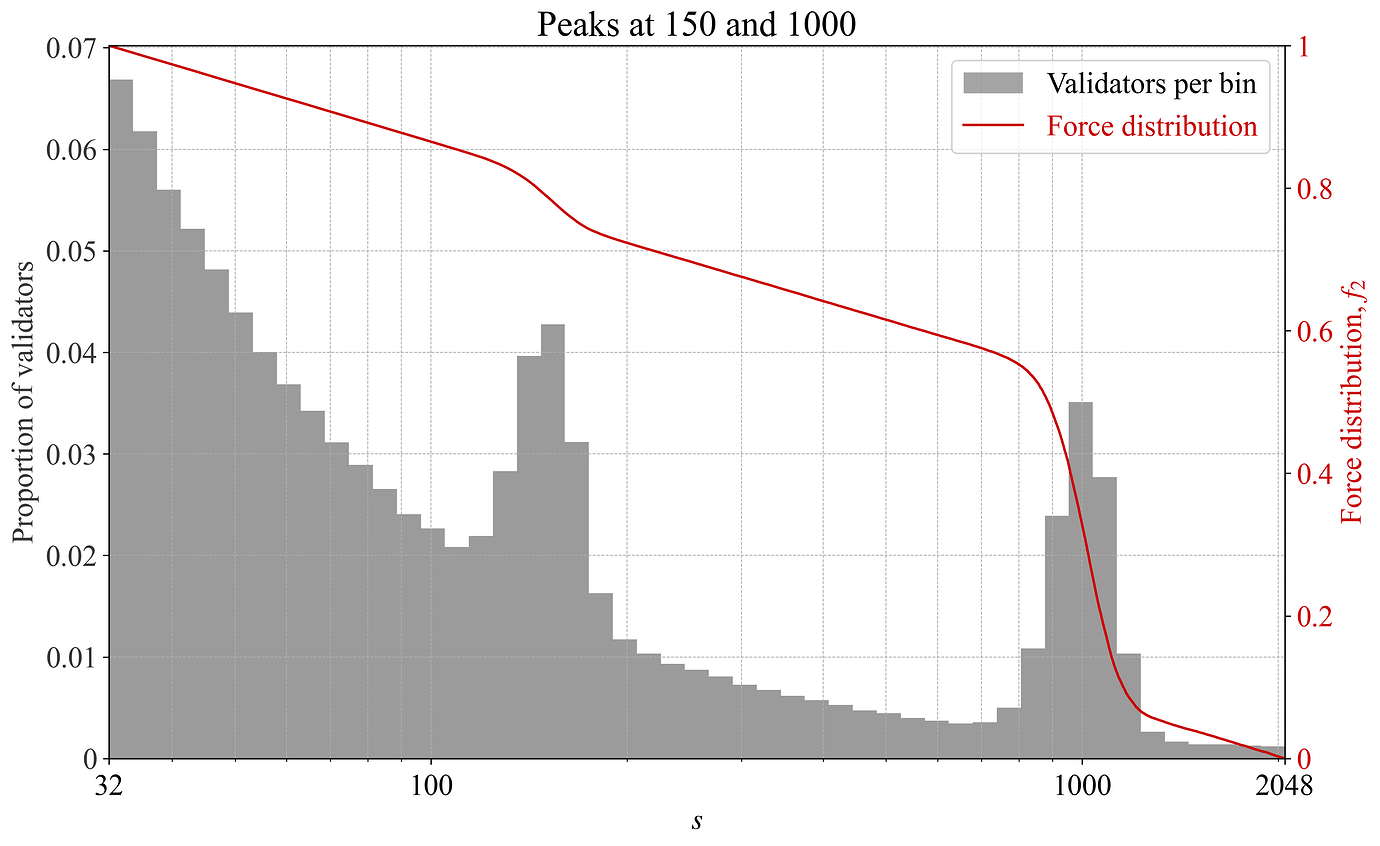 \
Figure 93497×2148 318 KB
\
Figure 93497×2148 318 KB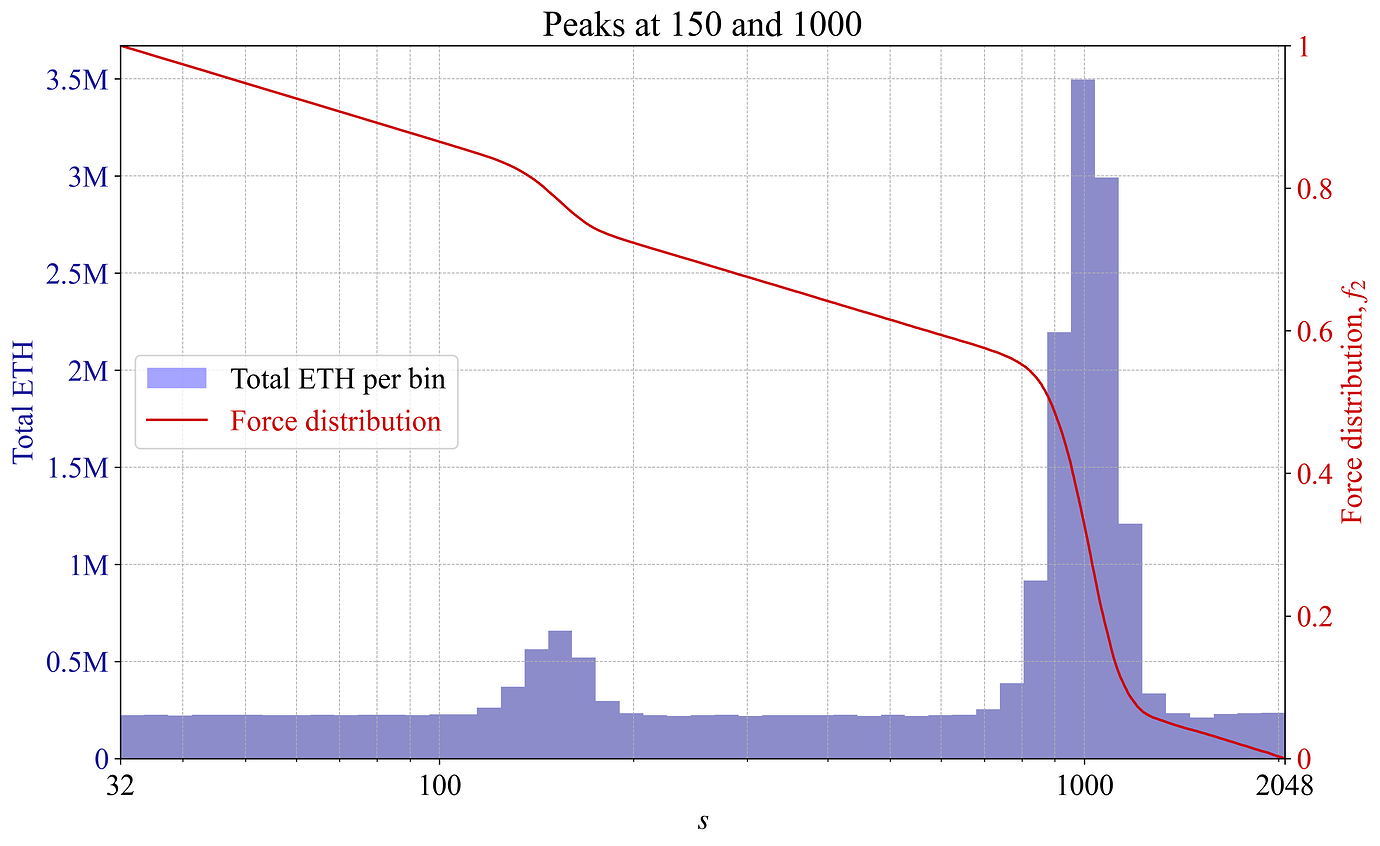 \
Figure 103496×2148 299 KB
\
Figure 103496×2148 299 KB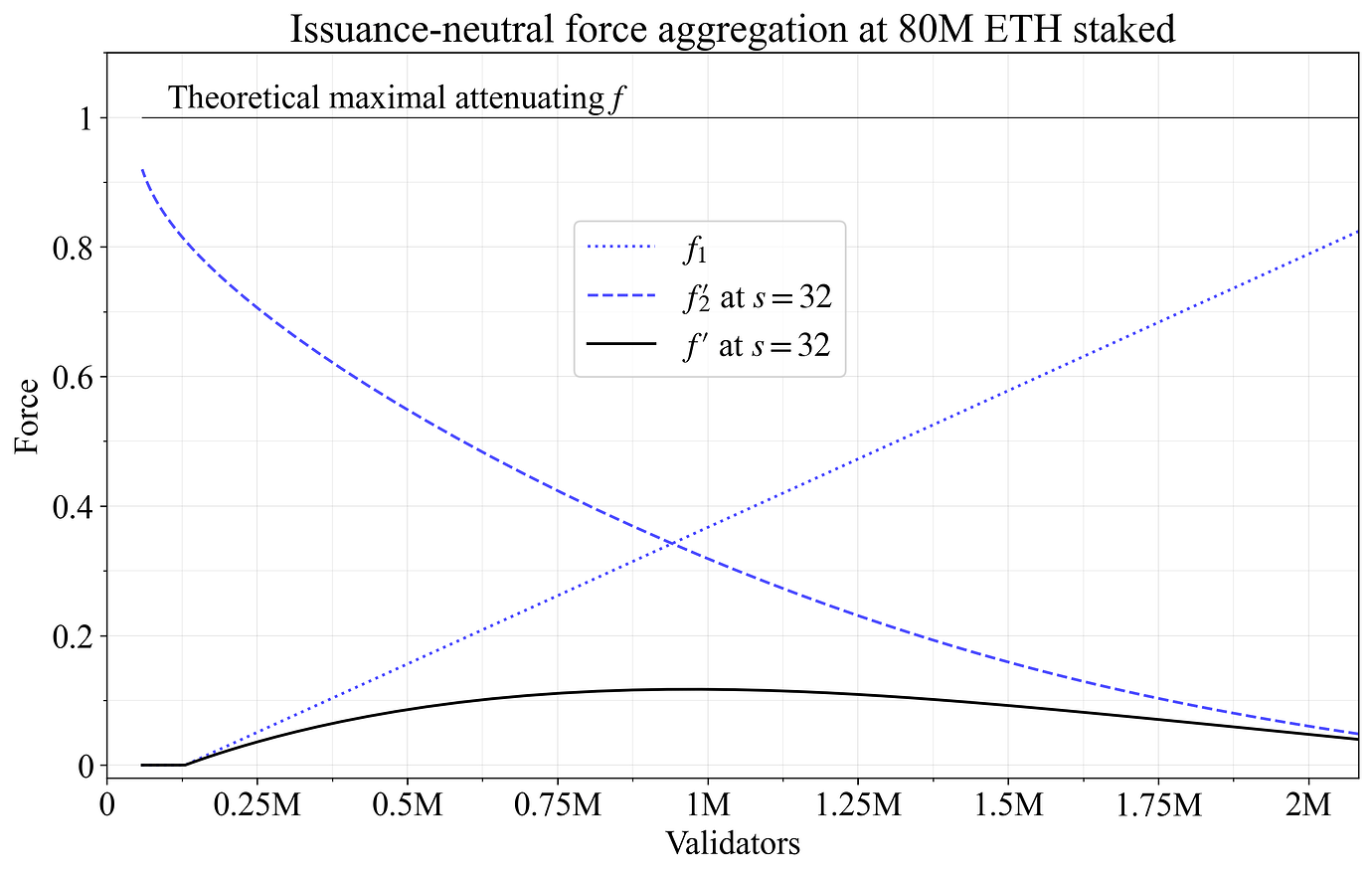 \
Figure 113058×1948 245 KB
\
Figure 113058×1948 245 KB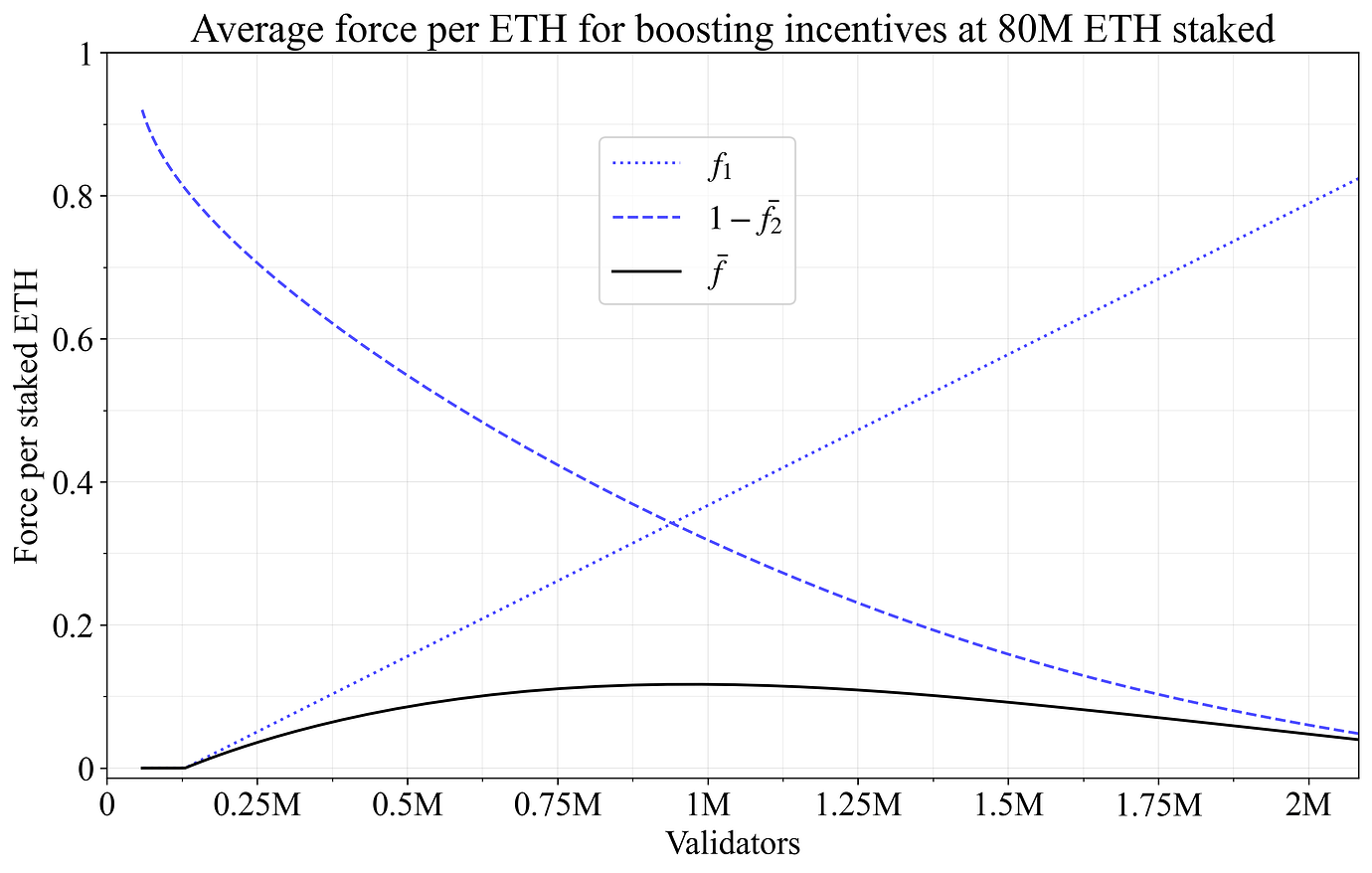 \
Figure 123058×1948 243 KB
\
Figure 123058×1948 243 KB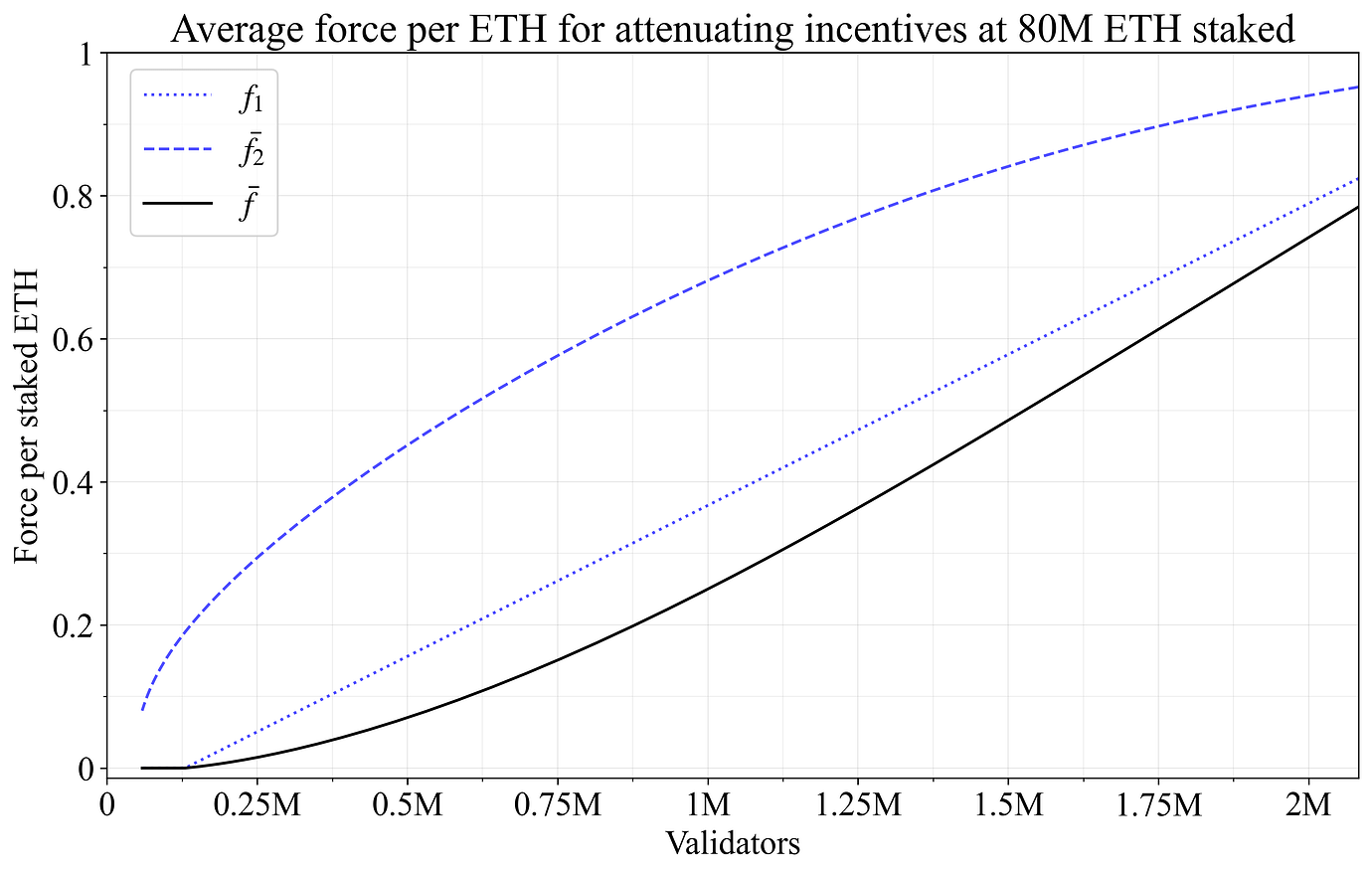 \
Figure 133058×1948 265 KB
\
Figure 133058×1948 265 KB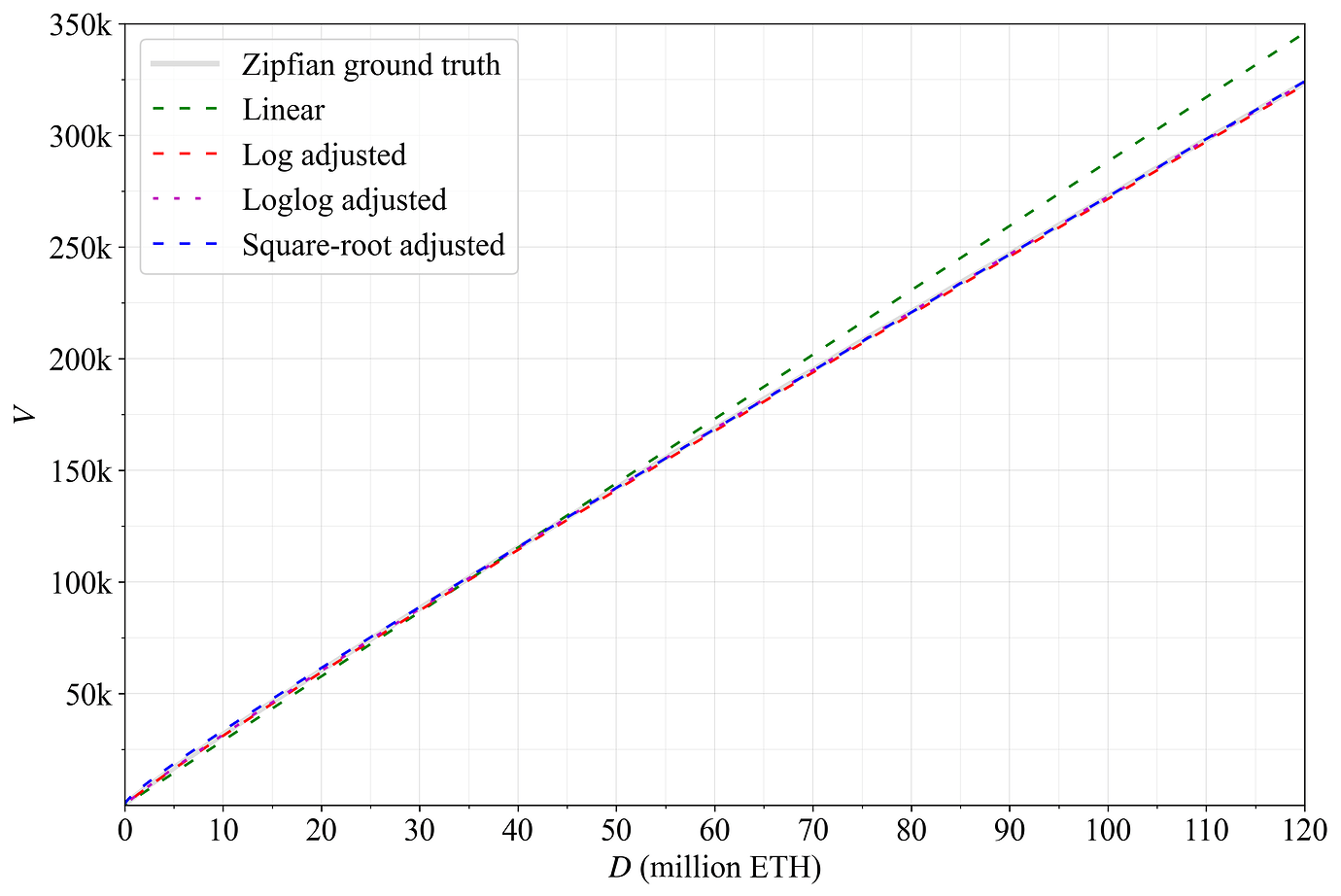 \
Figure A13171×2121 297 KB
\
Figure A13171×2121 297 KB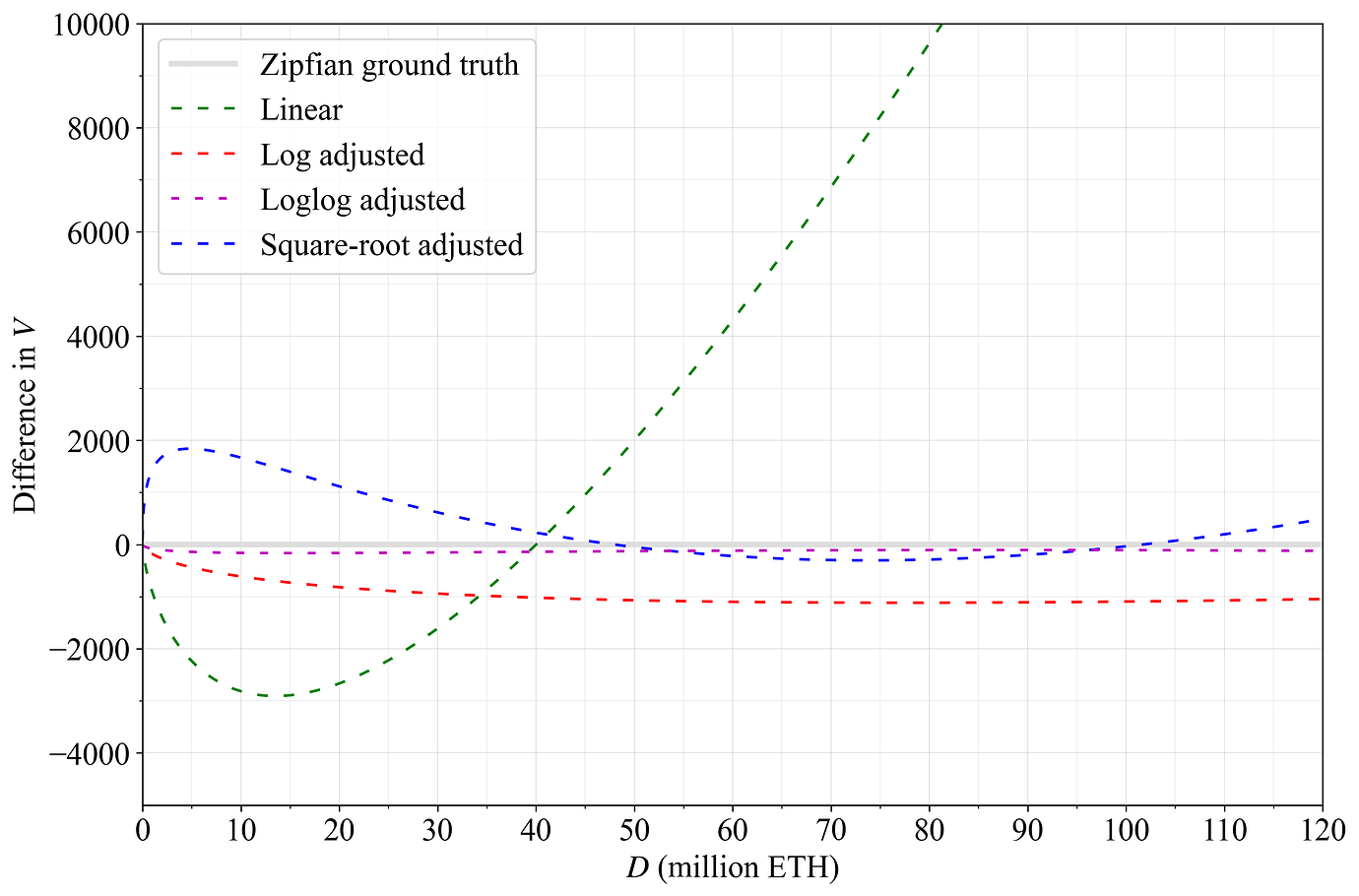 \
Figure A23213×2121 250 KB
\
Figure A23213×2121 250 KB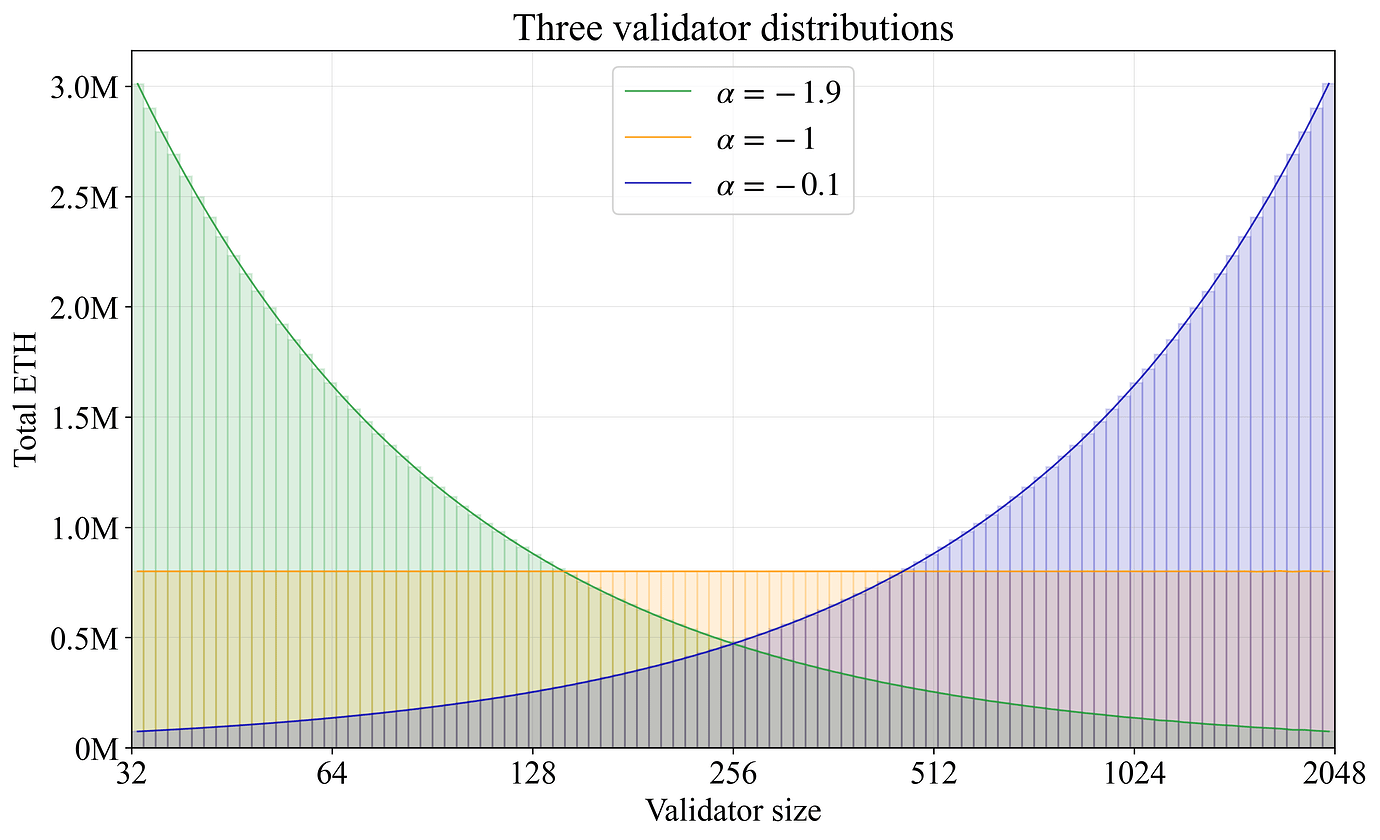 \
Figure C13200×1948 262 KB
\
Figure C13200×1948 262 KB
